Coburn J.W., Herdlick J.D. College Algebra: Graphs and Models
Подождите немного. Документ загружается.


28. a.
b.
c.
29. a.
b.
c.
30. a.
b.
c.
Multiply and write your answer in form.
31. a. b.
32. a. b.
33. a. b.
34. a. b.
35. a. b.
36. a. b.
Compute the special products.
37. a.
b.
38. a.
b.
39. a.
b.
40. a.
b.
41. a. b.
42. a. b.
43. a. b.
44. a. b.
For each complex number given, name the complex
conjugate and compute the product.
45. a. b.
46. a. b. 1 i15
2 i
3 i12
4 5i
12 i13
2
2
12 5i2
2
13 i122
2
12 5i2
2
13 i2
2
12 i2
2
13 4i2
2
12 3i2
2
1
1
2
3
4
i21
1
2
3
4
i2
15 i13
215 i132
1
1
6
2
3
i21
1
6
2
3
i2
13 i12
213 i122
12 i212 i2
12 7i212 7i2
17 5i217 5i2
14 5i214 5i2
14 i217 2i215 2i217 3i2
13 2i211 i213 2i212 3i2
12 3i215 i214 2i213 2i2
6i13 7i27i15 3i2
713 5i2312 3i2
14i214i25i
#
13i2
a ⴙ bi
a4
5
6
ib a13
3
8
ib
a3
3
5
ib a11
7
15
ib
19.4 8.7i2 16.5 4.1i2
a6
5
8
ib a4
1
2
ib
a8
3
4
ib a7
2
3
ib
13.7 6.1i2 11 5.9i2
12.5 3.1i2 14.3 2.4i2
17 4i2 12 3i2
12 5i2 13 i2
47. a. b.
48. a. b.
Use substitution to determine if the value shown is a
solution to the given equation. Use a calculator check
for Exercises 57 to 60.
49.
50.
51.
52.
53.
54.
55.
56.
57.
58.
59. Verify that is a solution to
Then show its complex
conjugate is also a solution.
60. Verify that is a solution to
Then show its complex
conjugate is also a solution.
Simplify using powers of i.
61. a. b. c. d.
62. a. b. c. d.
Divide and write your answer in form. Check
your answer using multiplication.
63. a. b.
64. a. b.
65. a. b.
66. a. b.
67. a. b.
68. a. b.
3 2i
6 4i
4 8i
2 4i
2 3i
3i
3 4i
4i
7
7 2i
6
1 3i
5
2 3i
7
3 2i
3
2 19
2
1 14
4
125
2
149
a ⴙ bi
i
65
i
19
i
50
i
36
i
53
i
39
i
26
i
48
2 3i12
x
2
4x 22 0.
x 2 3i12
1 4i
x
2
2x 17 0.
x 1 4i
x 1 i13
x
2
2x 4 0;
x 2 i15
x
2
4x 9 0;
x 1 3ix
2
6x 11 0;
x 1 2ix
2
2x 5 0;
x 1 2i1x 12
2
4;
x 3 3i1x 32
2
9;
x 5ix
2
25 0;
x 7ix
2
49 0;
x 4x
2
16 0;
x 6x
2
36 0;
3
4
1
5
i5i
1
2
2
3
i7i
290 CHAPTER 3 Quadratic Functions and Operations on Functions 3–10
College Algebra Graphs & Models—
cob19545_ch03_281-292.qxd 8/10/10 6:04 PM Page 290

3–11 Section 3.1 Complex Numbers 291
College Algebra Graphs & Models—
䊳
WORKING WITH FORMULAS
69. Absolute value of a complex number:
The absolute value of any complex number
(sometimes called the modulus of the number) is
computed by taking the square root of the sum of
the squares of a and b. Find the absolute value of
the given complex numbers.
a. b.
c.
|
3 i12
|
|
4 3i
||
2 3i
|
a bi
円a ⴙ bi円 ⴝ 2a
2
ⴙ b
2
70. Binomial cubes:
The cube of any binomial can be found using the
formula shown, where A and B are the terms of the
binomial. Use the formula to compute (note
and B 2i2.A 1
11 2i2
3
1A B2
3
A
3
3A
2
B 3AB
2
B
3
䊳
EXTENDING THE CONCEPT
79. Up to this point, we’ve said that expressions like
and are factorable:
and
while and are prime. More correctly,
we should state that and are
nonfactorable using real numbers, since they
p
2
7x
2
9
p
2
7x
2
9
p
2
7 1p 1721p 172,
x
2
9 1x 321x 32
p
2
7x
2
9
actually can be factored if complex numbers are
used. Specifically,
and
a. Verify that in general,
.1a bi21a bi2 a
2
b
2
1p i1721p i172 p
2
7.
1x 3i21x 3i2 x
2
9
䊳
APPLICATIONS
71. Dawn of imaginary numbers: In a day when
imaginary numbers were imperfectly understood,
Girolamo Cardano (1501–1576) once posed the
problem, “Find two numbers that have a sum of 10
and whose product is 40.” In other words,
and Although the solution
is routine today, at the time the problem posed an
enormous challenge. Verify that
and satisfy these conditions.
72. Verifying calculations using i: Suppose Cardano
had said, “Find two numbers that have a sum of 4
and a product of 7” (see Exercise 71). Verify that
and satisfy these
conditions.
Although it may seem odd, complex numbers have
several applications in the real world. Many of these
involve a study of electrical circuits, in particular
alternating current or AC circuits. Briefly, the
components of an AC circuit are current I (in amperes),
voltage V (in volts), and the impedance Z (in ohms). The
impedance of an electrical circuit is a measure of the
total opposition to the flow of current through the
circuit and is calculated as Z ⴝ R ⴙ iX
L
ⴚ iX
C
where R
represents a pure resistance, X
C
represents the
capacitance, and X
L
represents the inductance. Each of
these is also measured in ohms (symbolized by ).
B 2 i13A 2 i13
B 5 i115
A 5 i115
AB 40.A B 10
73. Find the impedance Z if and
74. Find the impedance Z if
and
The voltage V (in volts) across any element in an AC
circuit is calculated as a product of the current I and the
impedance Z:
75. Find the voltage in a circuit with a current
amperes and an impedance of
76. Find the voltage in a circuit with a current
amperes and an impedance of
In an AC circuit, the total impedance (in ohms) is given
by where Z represents the total impedance
of a circuit that has and wired in parallel.
77. Find the total impedance Z if and
78. Find the total impedance Z if and
Z
2
2 i.
Z
1
3 i
Z
2
3 2i.
Z
1
1 2i
Z
2
Z
1
Z ⴝ
Z
1
Z
2
Z
1
ⴙ Z
2
,
Z 4 2i .
I 2 3i
Z 5 5i .
I 3 2i
V ⴝ IZ.
X
C
8.3 .
X
L
5.6 ,R 9.2 ,
X
C
11 .
X
L
6 ,R 7 ,
cob19545_ch03_281-292.qxd 11/25/10 3:26 PM Page 291

Use this idea to factor the following.
b. c.
d. e.
80. In this section, we noted that the product property of
radicals can still be applied when
at most one of the factors is negative. So what
happens if both are negative? First consider the
expression What happens if you first
multiply in the radicand, then compute the square
root? Next consider the product .
Rewrite each factor using the i notation, then
compute the product. Do you get the same result as
before? What can you say about and
14
#
125?
14
#
25
125
#
14
14
#
25.
1AB
1A1B,
4x
2
49n
2
12
m
2
3x
2
36
81. Simplify the expression
82. While it is a simple concept for real numbers, the
square root of a complex number is much more
involved due to the interplay between its real and
imaginary parts. For the square root of
z can be found using the formula:
where the sign
is chosen to match the sign of b (see Exercise 69).
Use the formula to find the square root of each
complex number, then check by squaring.
a. b.
c. z 4 3i
z 5 12iz 7 24i
1z
12
2
11
冟
z
冟
a i1
冟
z
冟
a2,
z a bi
i
17
13 4i2 3i
3
11 2i2
2
.
292 CHAPTER 3 Quadratic Functions and Operations on Functions 3–12
College Algebra Graphs & Models—
䊳
MAINTAINING YOUR SKILLS
83. (1.4) Two boats leave Nawiliwili (Kauai) at the
same time, traveling in opposite directions. One
travels at 15 knots (nautical miles per hour) and the
other at 20 knots. How long until they are 196 mi
apart?
84. (2.4) State the domain of the following functions
using interval notation.
a. b.
c. f
1x2
x
x 3
f
1x2 x
3
2
f 1x2 x
2
3
85. (1.5) John can run 10 m/sec, while Rick can only
run 9 m/sec. If Rick gets a 2-sec head start, who
will reach the 200-m finish line first?
86. (R.4) Factor the following expressions completely.
a. b.
c. d. 4n
2
m 12nm
2
9m
3
x
3
x
2
x 1
n
3
27x
4
16
3.2 Solving Quadratic Equations and Inequalities
In Section R.4 we reviewed how to solve polynomials by factoring and applying the
zero factor property. While this is an extremely valuable skill, many polynomials are
unfactorable, and a more general method for finding solutions is necessary. We begin
our search here, with the family of quadratic polynomials (degree 2).
A. Zeroes of Quadratic Functions and x-Intercepts
of Quadratic Graphs
Understanding quadratic equations and functions is an important step towards a more
general study of polynomial functions. Due to their importance, we begin by restating
their definition:
Quadratic Equations
A quadratic equation is one that can be written in the form
where a, b, and c are real numbers and a 0.
ax
2
bx c 0,
LEARNING OBJECTIVES
In Section 3.2 you will see how we can:
A. Establish a relationship
between zeroes of a
quadratic function and the
x-intercepts of its graph
B. Solve quadratic equations
using the square root
property of equality
C. Solve quadratic equations
by completing the square
D. Solve quadratic equations
using the quadratic formula
and the discriminant
E. Solve quadratic inequalities
F. Solve applications of
quadratic functions and
inequalities
cob19545_ch03_281-292.qxd 11/25/10 3:26 PM Page 292
College Algebra G&M—
As shown, the equation is in standard form, meaning the terms are in decreasing
order of degree and the equation is set equal to zero. The family of quadratic functions
is similarly defined.
Quadratic Functions
A quadratic function is one that can be written in the form
where a, b, and c are real numbers and
In Section R.4, we noted that some quadratic equations have two real solutions, others
have only one, and still others have none. When these possibilities are explored graph-
ically, we note a clear connection between the zeroes of a quadratic function and the
x-intercepts of its graph.
EXAMPLE 1
䊳
Noting Relationships between Zeroes and x-Intercepts
Consider the functions and .
a. Find the zeroes of each function algebraically.
b. Find the x-intercepts of each function graphically.
c. Comment on how the zeroes and x-intercepts are related.
Solution
䊳
a. To find the zeroes algebraically, replace f(x) and g(x) with 0, then solve. In
each case, the solutions can be found by factoring.
For f(x): For g(x):
There are two real solutions, There is only one real solution,
and . but it is repeated twice.
b. To find the x-intercepts, go to the screen and enter the first function as Y
1
with (the x-axis), then graph them in the standard window. Locate the
x-intercepts using the (CALC) 5:Intersect feature.
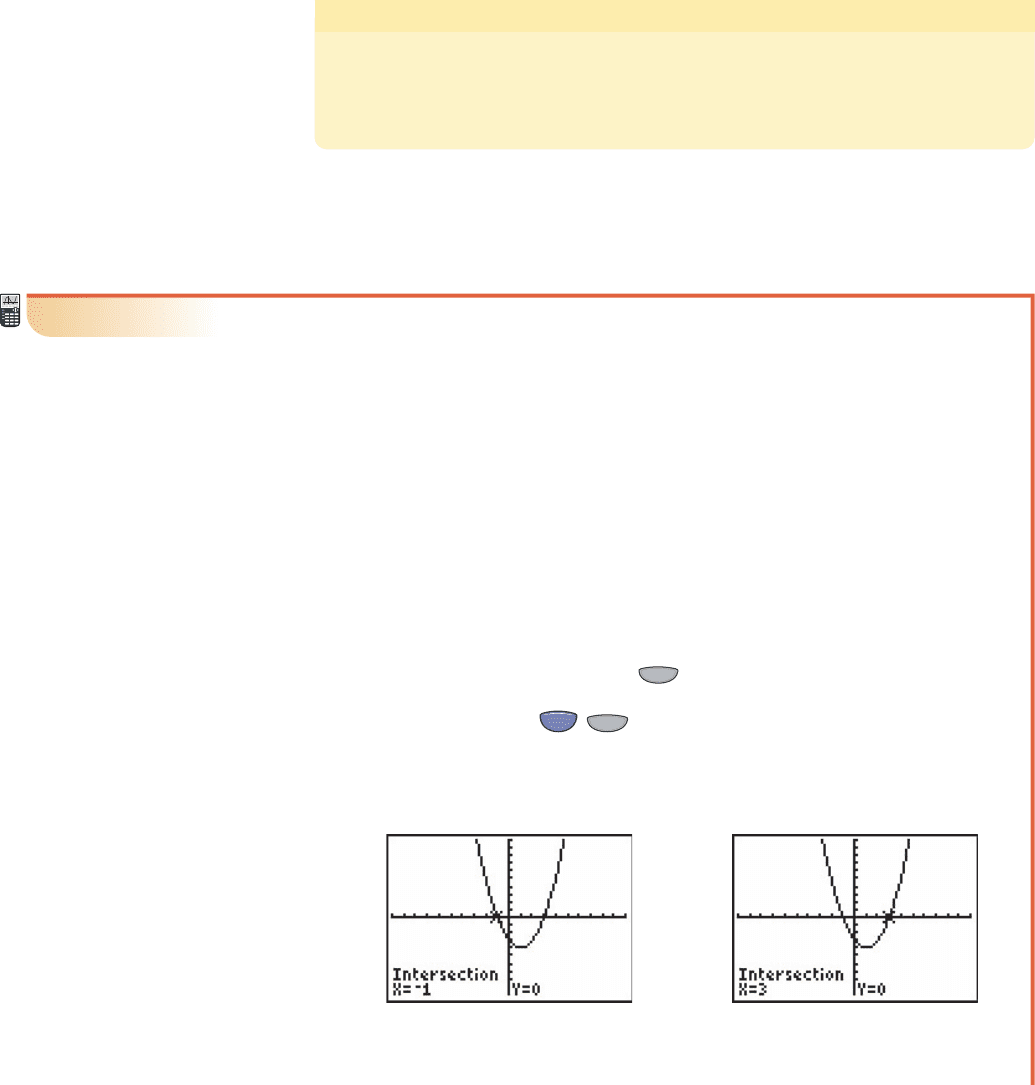
• For
The result shows there are two x-intercepts, which occur at (Figure 3.9)
and (Figure 3.10). These were also the real zeroes of f
1x2⫽ x
2
⫺ 2x ⫺ 3.x ⫽ 3
x ⫽⫺1
10
⫺10
⫺10
10
Figure 3.9
10
⫺10
⫺10
10
Figure 3.10
f 1x2⫽ x
2
⫺ 2x ⫺ 3
TRACE
2nd
Y
2
⫽ 0
Y=
x ⫽⫺1x ⫽ 3
x ⫽ 2 or x ⫽ 2x ⫽ 3 or x ⫽⫺1
1x ⫺ 221x ⫺ 22⫽ 0 1x ⫺ 321x ⫹ 12⫽ 0
x
2
⫺ 4x ⫹ 4 ⫽ 0 x
2
⫺ 2x ⫺ 3 ⫽ 0
g1x2⫽ x
2
⫺ 4x ⫹ 4f 1x2⫽ x
2
⫺ 2x ⫺ 3
a ⫽ 0.
f
1x2⫽ ax
2
⫹ bx ⫹ c,
3–13 Section 3.2 Solving Quadratic Equations and Inequalities 293
cob19545_ch03_293-313.qxd 8/10/10 6:06 PM Page 293
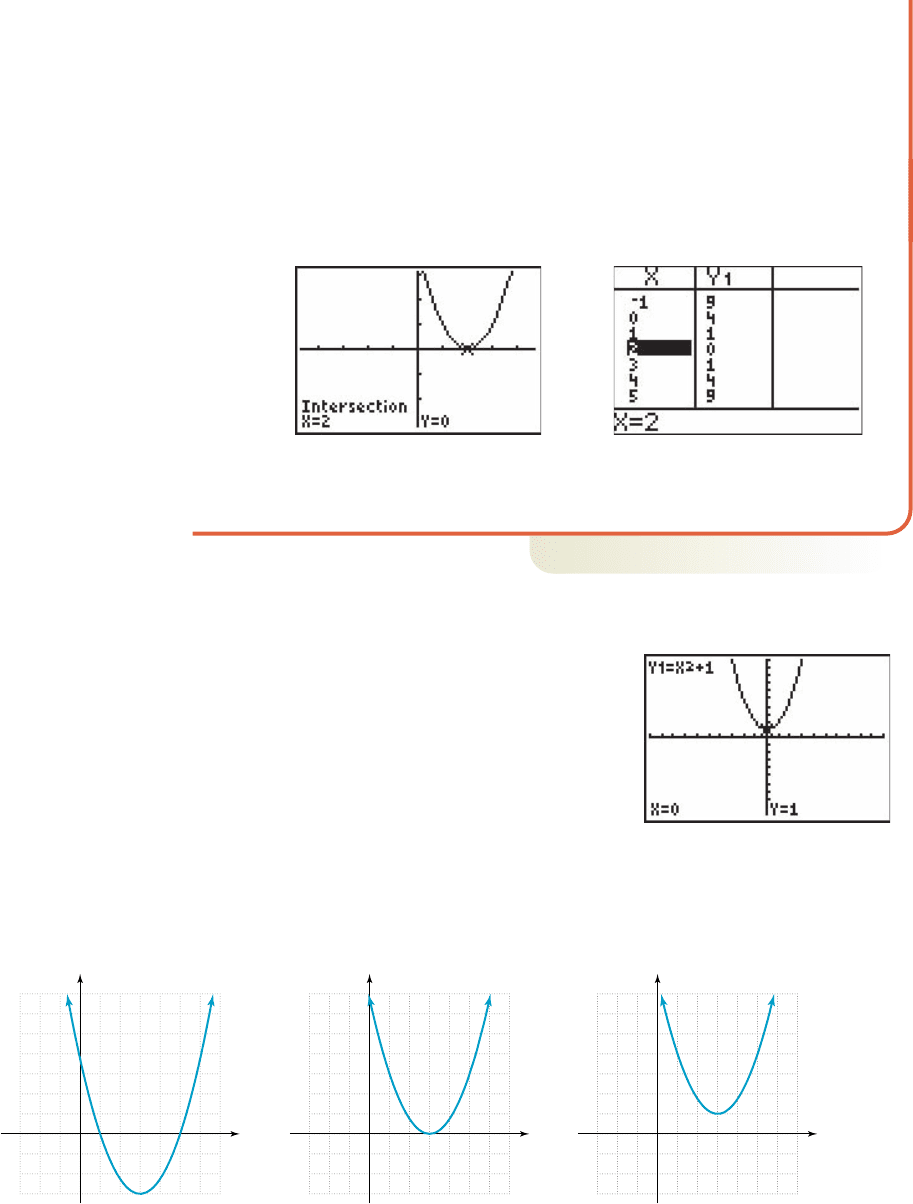
• For
After entering as Y
1
(leaving ) we again graph both functions
in the standard window. This time we find there is only one x-intercept, located at
(Figure 3.11), a fact supported by the accompanying table (Figure 3.12).
The graph is tangent to the x-axis at (touching the axis at just this one
point) and a closer look at g reveals why—the function is easily rewritten as
, producing the zero at and positive values for all other
inputs! Note that was the only zero found for .
c. From parts (a) and (b), it’s apparent that the real zeroes of a function appear
graphically as x-intercepts.
Now try Exercises 7 through 20
䊳
In Section 3.1, we noted that the equation
had no real solutions, indicating
the function has no real zeroes.
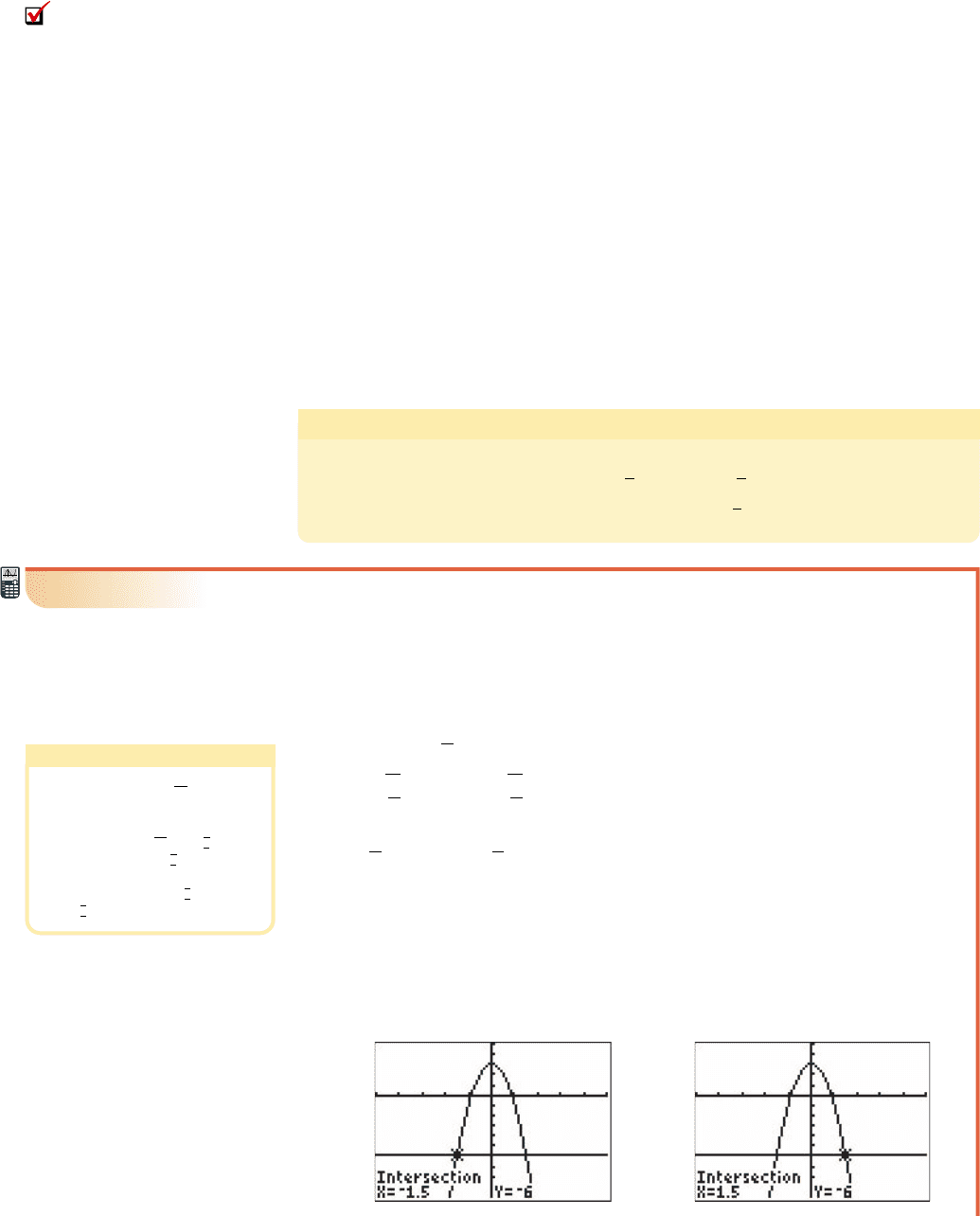
Here we might wonder whether a graphical
connection also exists for the “no real zeroes”
case. The graph of is given
in Figure 3.13 and shows that f has no
x-intercepts, further affirming the graphical
connection noted in Example 1. A summary of
these connections is shown in Figure 3.14 for
the case where (the graph opens up-
ward). Similar statements can be made when
(the graph opens downward).a 6 0
a 7 0
f
1x2⫽ x
2
⫹ 1
f
1x2⫽ x
2
⫹ 1
x
2
⫹ 1 ⫽ 0
5
3
⫺3
⫺5
Figure 3.11
Figure 3.12
g1x2⫽ x
2
⫺ 4x ⫹ 4x ⫽ 2
x ⫽ 2g1x2⫽ 1x ⫺ 22
2
x ⫽ 2
x ⫽ 2
Y
2
⫽ 0x
2
⫺ 4x ⫹ 4
g1x2⫽ x
2
⫺ 4x ⫹ 4
Figure 3.13
Figure 3.14
294 CHAPTER 3 Quadratic Functions and Operations on Functions 3–14
College Algebra G&M—
10
10
10
10
73
3
7
x
y
73
3
7
x
y
73
3
7
x
y
has two x-intercepts
and two real zeroes;
has two real solutions.
ax
2
⫹ bx ⫹ c ⫽ 0
f 1x2⫽ ax
2
⫹ bx ⫹ c
has one x-intercept
and one real repeated zero;
has one real repeated solution.
ax
2
⫹ bx ⫹ c ⫽ 0
g1x2⫽ ax
2
⫹ bx ⫹ c
has no x-intercepts
and no real zeroes;
has no real solutions.
ax
2
⫹ bx ⫹ c ⫽ 0
h1x2⫽ ax
2
⫹ bx ⫹ c
cob19545_ch03_293-313.qxd 8/10/10 6:06 PM Page 294
Also from our work in Example 1, we learn that the following statements are equiva-
lent, meaning that if any one of the statements is true, then all four statements are true.
For any real number r,
1. is a solution of .
2. r is a zero of .
3. is a factor of .
4. (r, 0) is an x-intercept of the graph of f.
B. Quadratic Equations and the Square Root Property of Equality
In Section 1.5 we solved the equation for x to establish a general solution
for equations of this form. In this section, we’ll establish a general solution for
using a process known as completing the square. To begin, we note
that the equation can be solved by factoring. In standard form we have
(note then The solutions are or
which are simply the positive and negative square roots of 9. This result sug-
gests an alternative method for solving equations of the form known as the
square root property of equality.
Square Root Property of Equality
If X represents an algebraic expression and
then or
also written as
EXAMPLE 2
䊳
Solving an Equation Using the Square Root Property of Equality
Use the square root property of equality to solve each equation. Verify solutions
graphically.
a. b. c.
Solution
䊳
a. original equation
subtract 3, divide by ⴚ4
or square root property of equality
or simplify radicals
This equation has two rational solutions.
Using the Intersection Method with and , we note
the graphs intersect at two points. This shows there will be two real roots,
which turn out to be rational (Figures 3.15 and 3.16).
Y
2
⫽⫺6Y
1
⫽⫺4x
2
⫹ 3
x ⫽⫺
3
2
x ⫽
3
2
x ⫽⫺
A
9
4
x ⫽
A
9
4
x
2
⫽
9
4
⫺4x
2
⫹ 3 ⫽⫺6
1x ⫺ 52
2
⫽ 7x
2
⫹ 12 ⫽ 0⫺4x
2
⫹ 3 ⫽⫺6
X ⫽⫾1k
X ⫽⫺1k;X ⫽ 1k
X
2
⫽ k,
X
2
⫽ k,
x ⫽ 3,
x ⫽⫺31x ⫹ 321x ⫺ 32⫽ 0.b ⫽ 02,x
2
⫺ 9 ⫽ 0
x
2
⫽ 9
ax
2
⫹ bx ⫹ c ⫽ 0
ax ⫹ b ⫽ c
f
1x21x ⫺ r2
f
1x2
f
1x2⫽ 0x ⫽ r
3–15 Section 3.2 Solving Quadratic Equations and Inequalities 295
College Algebra G&M—
A. You’ve just seen how
we can establish a relationship
between the zeroes of a
quadratic function and the
x-intercepts of its graph
5
5
⫺10
⫺5
5
5
⫺10
⫺5
Figure 3.15 Figure 3.16
WORTHY OF NOTE
In Section R.6 we noted that for
any real number a, From
Example 2(a), solving the equation
by taking the square root of both
sides produces This is
equivalent to again
showing this equation must have
two solutions, and
x ⫽ 2
9
4
.
x ⫽⫺2
9
4
冟
x
冟
⫽ 2
9
4
,
2x
2
⫽ 2
9
4
.
2a
2
⫽
冟
a
冟
.
cob19545_ch03_293-313.qxd 8/10/10 6:06 PM Page 295
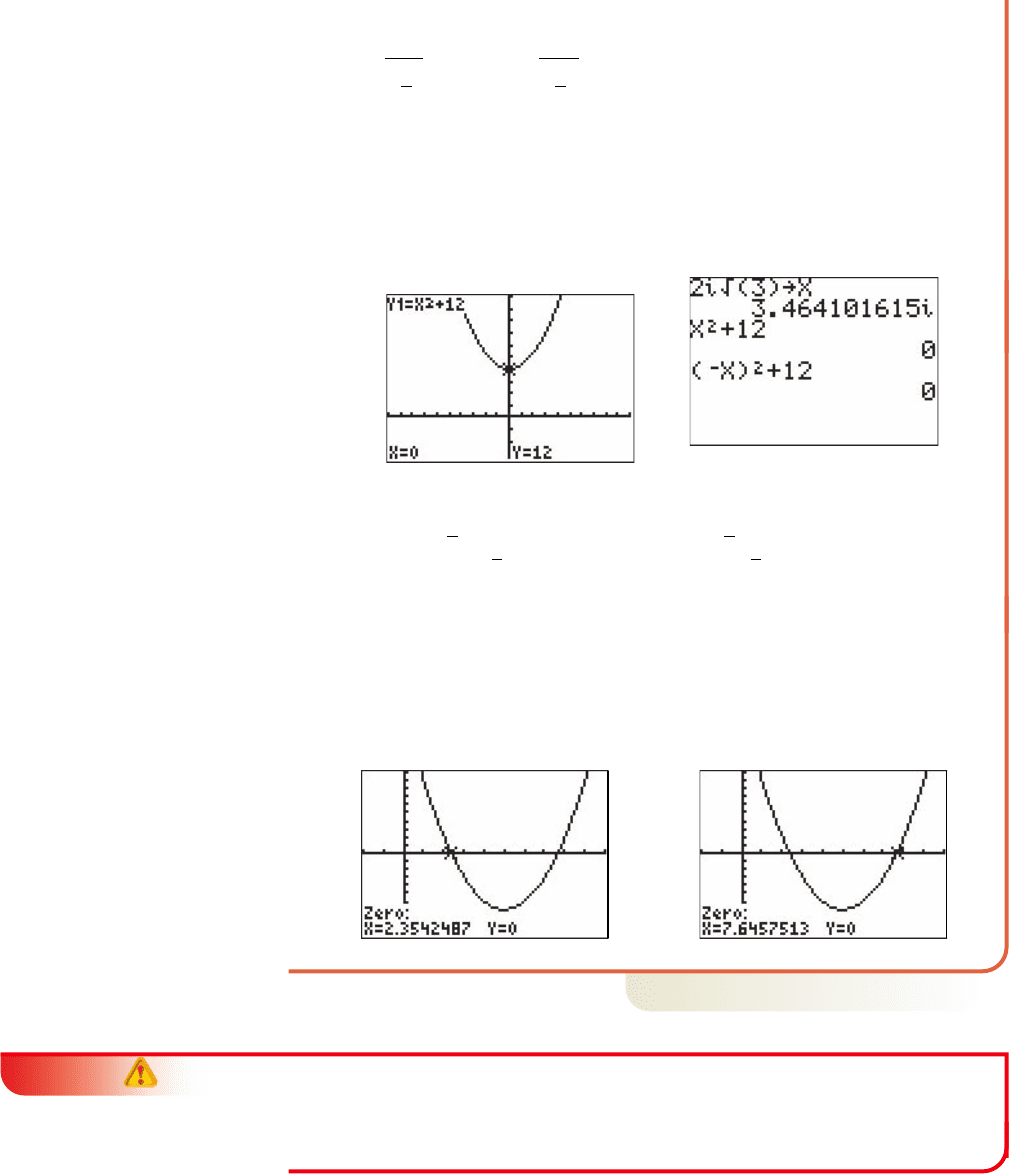
b. original equation
subtract 12
or square root property of equality
or simplify radicals
This equation has two complex solutions.
Using the Zeroes Method with shows there are no x-intercepts,
and therefore no real roots (Figure 3.17). However, the roots can still be
checked on the home screen, as shown in Figure 3.18.
Y
1
⫽ x
2
⫹ 12
x ⫽⫺2i13
x ⫽ 2i13
x ⫽⫺1⫺12 x ⫽ 1⫺12
x
2
⫽⫺12
x
2
⫹ 12 ⫽ 0
c.
original equation
or square root property of equality
solve for
x
This equation has two irrational solutions.
Using the Zeroes Method with , we note the graph has two
x-intercepts. This shows there will be two real roots, which turn out to be
irrational (Figures 3.19 and 3.20).
Y
1
⫽ 1x ⫺ 52
2
⫺ 7
x ⫽ 5 ⫺ 27
x ⫽ 5 ⫹ 27
x ⫺ 5 ⫽⫺17 x ⫺ 5 ⫽ 17
1x ⫺ 52
2
⫽ 7
Now try Exercises 21 through 36
䊳
CAUTION
䊳
For equations of the form as in Example 2(c), you should resist the tempta-
tion to expand the binomial square in an attempt to simplify the equation and solve by
factoring—many times the result is nonfactorable. Any equation of the form
can quickly be solved using the square root property of equality.
1x ⫹ d2
2
⫽ k
1x ⫹ d2
2
⫽ k
296 CHAPTER 3 Quadratic Functions and Operations on Functions 3–16
College Algebra G&M—
10
30
⫺10
⫺10
Figure 3.17 Figure 3.18
10
10
⫺10
⫺2
10
10
⫺10
⫺2
Figure 3.19 Figure 3.20
cob19545_ch03_293-313.qxd 8/10/10 6:06 PM Page 296

Answers written using radicals are called exact or closed form solutions. Actually
checking the exact solutions is a nice application of fundamental skills. Let’s check
from Example 2(c).
check: original equation
substitute for
x
simplify
✓
result checks ( also checks)
C. Solving Quadratic Equations by Completing the Square
Again consider from Example 2(c). If we had first expanded the bino-
mial square, we would have obtained then in
standard form. Note that this equation cannot be solved by factoring. Reversing this
process leads us to a strategy for solving nonfactorable quadratic equations, by creat-
ing a perfect square trinomial from the quadratic and linear terms. This process is
known as completing the square. To transform back into
[which we would then rewrite as and solve], we
subtract 18 from both sides, then add 25:
subtract 18
add 25
factor, simplify
In general, after subtracting the constant term, the number that “completes the
square” is computed as : . For additional
practice finding this constant term, see Exercises 37 through 42.
EXAMPLE 3
䊳
Solving a Quadratic Equation by Completing the Square
Solve by completing the square:
Solution
䊳
original equation
standard form
subtract 13 to make room for new constant
compute (
linear coefficient
)
2
add 9 to both sides (completing the square)
factor and simplify
or square root property of equality
or simplify radicals and solve for
x
Now try Exercises 43 through 52
䊳
Based on our earlier work, we expect that the equation from Example 3 has no
x-intercepts. Using confirms this (Figure 3.21 following), but we
gain additional insight using the equation in its given form and the intersection-of-
graphs method. With and , we realize that if the graphs do not
intersect (Figure 3.22), there can likewise be no real roots!
Y
2
⫽ 6xY
1
⫽ x
2
⫹ 13
Y
1
⫽ x
2
⫺ 6x ⫹ 13
x ⫽ 3 ⫺ 2ix ⫽ 3 ⫹ 2i
x ⫺ 3 ⫽⫺1⫺4
x ⫺ 3 ⫽ 1⫺4
1x ⫺ 32
2
⫽⫺4
x
2
⫺ 6x ⫹ 9 ⫽⫺13 ⫹ 9
431
1
2
2 31
1
2
21⫺624
2
⫽ 9
x
2
⫺ 6x ⫹
___
⫽⫺13 ⫹
___
x
2
⫺ 6x ⫹ 13 ⫽ 0
x
2
⫹ 13 ⫽ 6x
x
2
⫹ 13 ⫽ 6x.
3
1
2
11024
2
⫽ 253
1
2
1coefficient of linear term24
2
1x ⫺ 52
2
⫽ 7
x
2
⫺ 10x ⫹ 25 ⫽⫺18 ⫹ 25
x
2
⫺ 10x ⫽⫺18
x
2
⫺ 10x ⫹ 18 ⫽ 0
1x ⫺ 52
2
⫽ 7x
2
⫺ 10x ⫹ 25 ⫽ 7
x
2
⫺ 10x ⫹ 18 ⫽ 0
x
2
⫺ 10x ⫹ 18 ⫽ 0x
2
⫺ 10x ⫹ 25 ⫽ 7,
1x ⫺ 52
2
⫽ 7
x ⫽ 5 ⫺ 17
1172
2
⫽ 7 7 ⫽ 7
117
2
2
⫽ 7
5 ⫹ 17 15 ⫹ 17 ⫺ 52
2
⫽ 7
1x ⫺ 52
2
⫽ 7
x ⫽ 5 ⫹ 17
3–17 Section 3.2 Solving Quadratic Equations and Inequalities 297
College Algebra G&M—
B. You’ve just seen how
we can solve quadratic
equations using the square
root property of equality
cob19545_ch03_293-313.qxd 8/10/10 6:06 PM Page 297
The process of completing the square can be applied to any quadratic equation
with a leading coefficient of 1. If the leading coefficient is not 1, we simply divide
through by a before beginning, which brings us to this summary of the process.
Completing the Square to Solve a Quadratic Equation
To solve by completing the square:
1. Subtract the constant c from both sides.
2. Divide both sides by the leading coefficient a.
3. Compute and add the result to both sides.
4. Factor left-hand side as a binomial square; simplify right-hand side.
5. Solve using the square root property of equality.
EXAMPLE 4
䊳
Solving Quadratic Equations
Find all solutions:
Algebraic Solution
䊳
Completing the Square
original equation
standard form (nonfactorable)
subtract 1
divide by ⴚ3
; add
factor and simplify
or square root property of equality
or solve for
x
and simplify (exact form)
or approximate form (to hundredths)
Graphical Solution
䊳
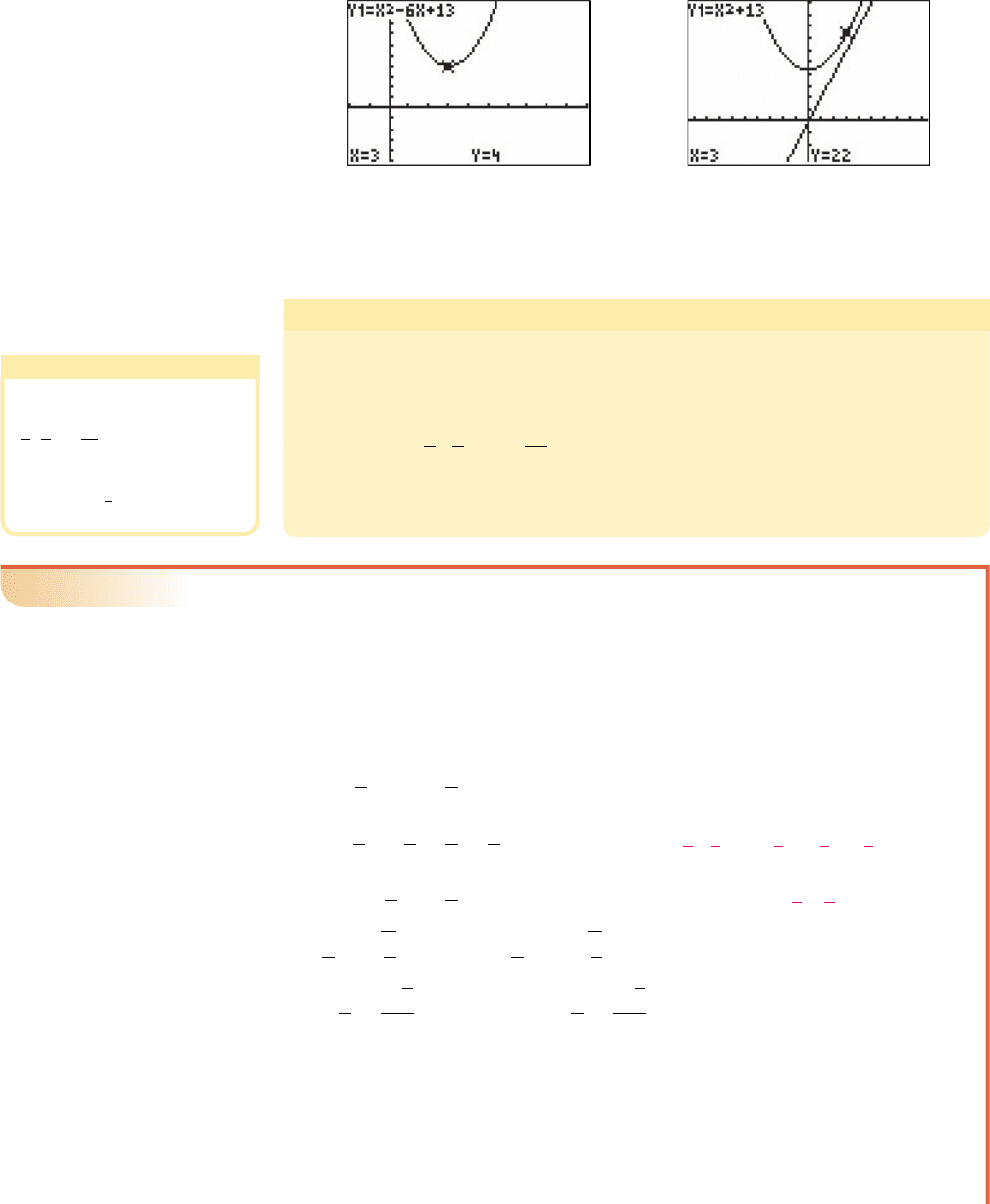
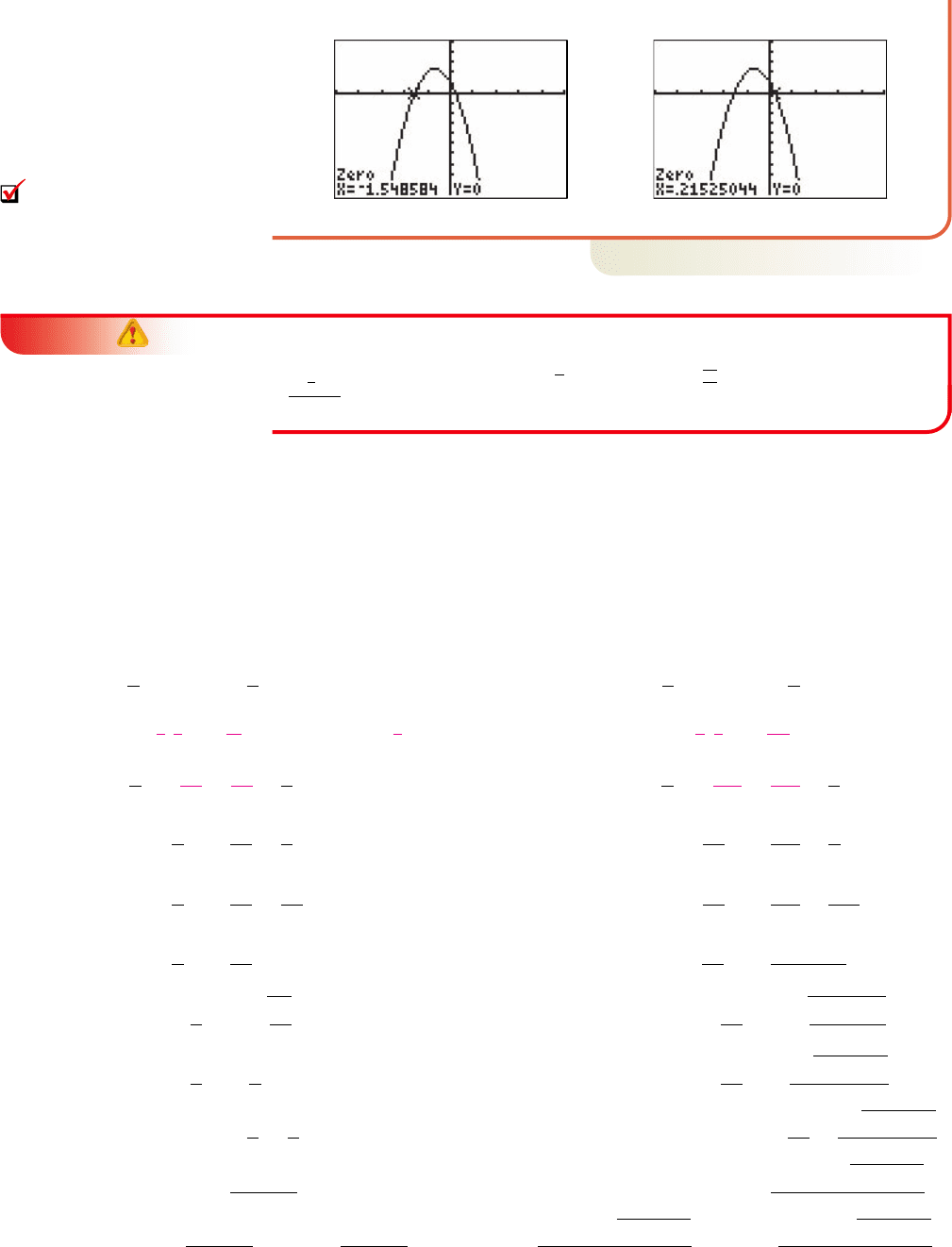
Zeroes Method
After writing the equation in standard form, we have . The
graph of has two x-intercepts, indicating there will be two
real roots. Locating the zeroes yields the decimal approximations shown and
confirms our calculated results (Figures 3.23 and 3.24).
Y
1
⫽⫺3x
2
⫺ 4x ⫹ 1
⫺3x
2
⫺ 4x ⫹ 1 ⫽ 0
x ⬇ ⫺1.55x ⬇ 0.22
x ⫽⫺
2
3
⫺
17
3
x ⫽⫺
2
3
⫹
17
3
x ⫹
2
3
⫽⫺
A
7
9
x ⫹
2
3
⫽
A
7
9
a
1
3
⫽
3
9
b ax ⫹
2
3
b
2
⫽
7
9
4
9
ca
1
2
b a
4
3
bd
2
⫽ a
2
3
b
2
⫽
4
9
x
2
⫹
4
3
x ⫹
4
9
⫽
1
3
⫹
4
9
x
2
⫹
4
3
x ⫹ ⫽
1
3
⫺3x
2
⫺ 4x ⫽⫺1
⫺3x
2
⫺ 4x ⫹ 1 ⫽ 0
⫺3x
2
⫹ 1 ⫽ 4x
⫺3x
2
⫹ 1 ⫽ 4x.
c
1
2
#
b
a
d
2
⫽ a
b
2a
b
2
ax
2
⫹ bx ⫹ c ⫽ 0
298 CHAPTER 3 Quadratic Functions and Operations on Functions 3–18
College Algebra G&M—
10
10
⫺5
⫺2
10
30
⫺10
⫺10
Figure 3.21 Figure 3.22
WORTHY OF NOTE
It’s helpful to note that the number
you’re squaring in step three,
turns out to be the
constant term in the factored form.
From Example 3, the number we
squared was , and the
binomial square was 1x ⫺ 32
2
.
1
1
2
21⫺62⫽ ⫺3
c
1
2
#
b
a
d⫽
b
2a
,
cob19545_ch03_293-313.qxd 8/10/10 6:06 PM Page 298
Now try Exercises 53 through 60
䊳
CAUTION
䊳
For many of the skills/processes needed in a study of algebra, it’s actually easier to work
with the fractional form of a number, rather than the decimal form. For example, comput-
ing is easier than computing , and finding is much easier than finding
.
D. The Quadratic Formula and the Discriminant
In Section 1.5 we found a general solution for the linear equation by compar-
ing it to Here we’ll use a similar idea to find a general solution for quad-
ratic equations. In a side-by-side format, we’ll solve the equations and
by completing the square. Note the similarities.
given equations
subtract constant term
divide by lead coefficient
add to both sides
left side factors as a binomial square
determine LCDs
simplify right side
square root property of equality
simplify radicals
solve for
x
combine terms
or solutions or x ⫽
⫺b ⫺ 2b
2
⫺ 4ac
2a
x ⫽
⫺b ⫹ 2b
2
⫺ 4ac
2a
x ⫽
⫺5 ⫺ 1
4
x ⫽
⫺5 ⫹ 1
4
x ⫽
⫺b ⫾ 2b
2
⫺ 4ac
2a
x ⫽
⫺5 ⫾ 1
4
x ⫽⫺
b
2a
⫾
2b
2
⫺ 4ac
2a
x ⫽⫺
5
4
⫾
1
4
x ⫹
b
2a
⫽⫾
2b
2
⫺ 4ac
2a
x ⫹
5
4
⫽⫾
1
4
x ⫹
b
2a
⫽⫾
B
b
2
⫺ 4ac
4a
2
x ⫹
5
4
⫽⫾
B
1
16
ax ⫹
b
2a
b
2
⫽
b
2
⫺ 4ac
4a
2
ax ⫹
5
4
b
2
⫽
1
16
ax ⫹
b
2a
b
2
⫽
b
2
4a
2
⫺
4ac
4a
2
ax ⫹
5
4
b
2
⫽
25
16
⫺
24
16
ax ⫹
b
2a
b
2
⫽
b
2
4a
2
⫺
c
a
ax ⫹
5
4
b
2
⫽
25
16
⫺
3
2
x
2
⫹
b
a
x ⫹
b
2
4a
2
⫽
b
2
4a
2
⫺
c
a
x
2
⫹
5
2
x ⫹
25
16
⫽
25
16
⫺
3
2
c
1
2
a
b
a
bd
2
⫽
b
2
4a
2
c
1
2
1linear coefficient2d
2
c
1
2
a
5
2
bd
2
⫽
25
16
x
2
⫹
b
a
x ⫹
___
⫽⫺
c
a
x
2
⫹
5
2
x ⫹
___
⫽⫺
3
2
ax
2
⫹ bx ⫹⫽⫺c 2 x
2
⫹ 5x ⫹⫽⫺3
ax
2
⫹ bx ⫹ c ⫽ 0 2 x
2
⫹ 5x ⫹ 3 ⫽ 0
ax
2
⫹ bx ⫹ c ⫽ 0
2x
2
⫹ 5x ⫹ 3 ⫽ 0
2x ⫹ 3 ⫽ 15.
ax ⫹ b ⫽ c
10.5625
2
9
16
10.6
2
2
1
2
3
2
2
3–19 Section 3.2 Solving Quadratic Equations and Inequalities 299
College Algebra G&M—
C. You’ve just seen how
we can solve quadratic
equations by completing the
square
5
5
⫺10
⫺5
5
5
⫺10
⫺5
Figure 3.23 Figure 3.24
cob19545_ch03_293-313.qxd 11/26/10 5:57 PM Page 299
