Чураков Е.П. Математические методы обработки экспериментальных данных в экономике

Подождите немного. Документ загружается.

мать так: при достаточно больших / рассчитанная по правилу

(3.82) величина Si будет меньше соответствующей величины/ на

P^i/a, т.е. расчетные значения «запаздывают» относительно ис-

тинных. Аналогичный анализ можно провести и при трендах с

более сложной моделью, выявив соответствующие ошибки. На-

личие ошибок говорит о том, что при отличии модели тренда от

(3.80) необходимо алгоритм экспоненциального сглаживания

(3.82) видоизменить таким образом, чтобы он оказался более

приспособленным к новой модели тренда, нежели (3.82). Такие

алгоритмы разработаны и, по существу, представляют собой мно-

гократное применение изложенного алгоритма экспоненциаль-

ного сглаживания. Приведем некоторые из них, не прибегая к де-

тальному анализу.

Пусть д = I, т.е. модель тренда представлена выражением

(3.88).

В этом случае алгоритм экспоненциального сглаживания

представлен двумя рекуррентными соотношениями:

Si = Si_^-^a(yi-Si_0, (3.93)

= Qi-i +

OL(Si-

a_i), / = 1,

2,...,

Л^,

(3.94)

из которых второе представляет собой также алгоритм экспонен-

циального сглаживания, но в предположении, что «входом» для

него служат «выходы» первого алгоритма. Для организации вы-

числений теперь нужно иметь два начальных условия. Они зада-

ются в виде:

^0=^00-—йю, Qo='Soo-—aiQ, (3.95)

где ^00, ^10

—

некоторые начальные оценки параметров модели

тренда. Их можно найти, например, методом наименьших квад-

ратов на основании небольшого числа начальных элементов об-

рабатываемого временного ряда. После обработки всего ряда

оценки параметров тренда находят по формулам:

Долг

= 25лг-

QN,

aijsi

= a(Sj^- Ол^)/р,

что позволяет прогноз выразить соотношением

= (2 + а(т -

N)/^)SN-

+ a(m - А0/Р)(2лг.

150

(3.96)

Заметим, что вычисления могут быть организованы не обяза-

тельно

терминах экспоненциальных средних (3.93), (3.94), но и

в терминах текущих оценок ао/ иац параметров модели ряда а^,

а\. Действительно, по аналогии с (3.95) имеем:

=aoi

- P5i//a,

=% -

2^au/a.

Подставив эти выражения в (3.93), (3.94), получим:

% - ^Sii/a =

ау1

+ Р(5о(/_1) -

^ащ^х)),

Soi

- 2pai//a = а(ао/ - &ац/а) + p(5o(/_i) - 2pai(/_i)/a).

Из этой системы находим:

% = ^о(/-1) + ^1(/-1) +

Р y^h ^/

^Д'/-

5о(/_1)

- 5i(/_i),

^1/

= ^1(/-1) +

осе/,

/= 1,

2,...,

Ж (3.97)

Аналогичные соотношения для тренда, описываемого поли-

номом второго порядка/- =

ло

^i^/

<^2^/V2,

приобретают вид:

е/=а-1

сх(5,-ам),

if, =

Л/_1

+ а(а -

Л/-1),

/ = 1,

2,...,

Л^

при

Р , Р(2-а)^

2р , р(3~2а)

^ а

. " . ЗР. Зр(4~3а).

^=^00~—^10+ 5 ^20>

« 2а^

текущие оценки:

aon=^3Sn-3Qn

Rn,

= а((6 -

5a)Sn

2(5

^ 4а)(3„ + (4 - Зa)Л,)/2p^

a2n-=a\Sn-2Q„+R^yf;

151

прогноз

Ущ

SON

^{m-N)axN-^{m- М)^а2м/2.

Как и в предыдущем случае, этот алгоритм может быть выра-

жен через текущие оценки параметров модели тренда.

3.6. Анализ адекватности модели тренда

временного ряда

Правильно обоснованная модель тренда в значительной степени

определяет успешность решения задачи прогнозирования вре-

менного ряда. К сожалению, универсальных рекомендаций по

выбору модели, гарантирующей последующий успех, нет. Интуи-

тивные догадки, следующие из результатов начального визуаль-

ного обзора рада, умозрительные заключения, основанные на

анализе природы ряда и обусловливающих его причинно-следст-

венных явлений, опыт решения прогностических задач, квали-

фикация исследователя

—

все это способствует удаче, приближа-

ет, но не обеспечивает ее. Поэтому часто оказывается целесооб-

разным задаться несколькими моделями, а в последующем, под-

вергнув их надлежащему дополнительному анализу, отдать пред-

почтение наиболее соответствующей (адекватной) результатам

наблюдений. Но для этого необходимо иметь набор критериев,

выявляющих данную адекватность. В подборе таких критериев

также нет общепризнанного мнения. Остановимся на одном час-

то практикуемом подходе. В его основе лежит исходная гипотеза

о том, что случайные составляющие

р/,

/ = 1,

2,...,

7V,

в составе ря-

да (3.1) образуют последовательность центрированных независи-

мых нормально распределенных случайных величин. Поэтому

если модель тренда выбрана удачно и правильно оценены ее па-

раметры, остаток ряда

=3^1

- S hN^kiU)^ i

h 2, ..., Л^, (3.98)

к=0

должен также образовывать последовательность типа дискретно-

го белого шума. Поэтому адекватной признают модель, которая

порождает остаточный ряд (3.98) со случайными центрирован-

ными некоррелированными нормально распределенными

152

элементами. Тогда проверка адекватности сводится к выявлению

перечисленных свойств остаточного

ряда.

Это осуществляется так.

Проверка случайности элементов остаточного ряда проводит-

ся по

критерию серий

или

критерию поворотных

точек.

При пер-

вом

из них

по

результатам сравнения

двух

соседних элементов ос-

таточного ряда составляется последовательность нулей и единиц.

Если первая разность

Ав/

= e/+i

—

е/

О,

то в последовательности

ставится нуль, иначе

—

единица. Далее подсчитывается число се-

рий v(AO, представляющих собой фрагменты последовательнос-

ти,

состоящие только из нулей или единиц, и продолжительность

^тах самой

ДЛИННОЙ

ссрии. Остаточный ряд с вероятностью 0,95

считается случайным, если

^тах<^0(А^);

v(^)>[(2iV-l)/3-2V(167V-29)/90].

Здесь/:о(ЛО =

при N<

k{^{N) = 6

при

7V>26;

[...] -символ це-

лой части.

При использовании менее строгого критерия поворотных то-

чек поступают

так:

сравнивают элемент ряда остатков

двумя со-

седними; если он окажется меньше или больше их, то соответст-

вующая точка признается поворотной; далее подсчитывается

число

всех поворотных

точек;

если окажется

s>[2(N-2)/3-2^j(l6N-29)/90],

остаточный ряд считается состоящим из случайных элементов.

Проверка центрированности проводится с использованием

t'Kpumepun

Стьюдента.

С этой целью формируется статистика

YH/WJVA^/O,,

(3.99)

ще

т.е.

среднее значение и среднеквадратичное отклонение остаточ-

ного

ряда.

Далее задаются уровнем значимости а

или

доверитель-

ной вероятностью 1 -- а и находят lOOa/2-процентную точку

wiooa/2 ^распределения

N—

степенями

свободы.

Если окажет-

ся у > wiooa/25 то гипотеза о центрированности остаточнохо ряда

153

отвергается как не соответствующая экспериментальным дан-

ным с вероятностью ошибиться а. При противоположном нера-

венстве ряд признается центрированным с вероятностью 1

—

правильности этого решения.

Проверка независимости уровней остаточного ряда преследует

цель подтвердить отсутствие систематической составляющей в

составе ряда и проводится с применением

критерия

Дарви-

на—Уотсона,

соответствии

этим критерием вычисляется вели-

чина

л^

(ек^-е^-О

к=2

k=l

= 3

N ^

k=2

k^l J

2(l-i?),

где

—

так называемый коэффициент

автокорреляции

первого по-

радка.

Таблица 3.1

Нижний

верхний di пороги

Объем

выборки

Л^

100

Сложность модели тренда q

1,08

1,20

1,35

1,50

1,65

1,36

1,41

1,49

1,59

1,69

0,95

1,10

1,28

1,46

1,63

1,54

1,57

1,63

1,72

0,82

1,00

1,21

1,42

1,61

1,75

1,68

1,65

1,67

1,71

0,69

1,90

1,14

1,38

1,59

1,97

1,83

1,74

1,72

1,76

0,56

0,79

1,07

1,34

1,57

2,21

1,99

1,83

1,47

1,78

Величина ^следующим образом подвергается анализу. Преж-

де всего если окажется

> 2, то заменяют dnad =4

—

f/и после-

дующая работа ведется с ^ по

тому же

алгоритму, что ncd.B рас-

смотрение вводятся два порога: нижний di и верхний

^2-

Значе-

ния этих порогов определяются объемом выборки N, сложностью

154

модели тренда

уровнем значимости а и при а = 0,05 система-

тизированы в

табл.

3.1 [27].

Если d (или d

)G(0,

d\), то это является признаком сильной

автокоррелированности элементов остаточного ряда, и предпо-

лагаемая

модель

тренда признается неадекватной. Если

d{d

{dj,

2),

то элементы остаточного ряда классифицируются как незави-

симые, а модель тренда - адекватной. При

d{d*)^{d\,

di) одно-

значный вывод не делается и применяют дополнительные мето-

ды исследования.

Дополнительный анализ проводят с использованием

корреля-

ционной функции

tim) остаточного ряда, которую определяют сле-

дующим образом:

г{т) =

N-m

A:=l

Значение этой функции R

r{\), называемое коэффициентом

автокорреляции, уже встречалось при формировании критерия

Дарбина-Уотсона, и оно же используется для анализа независи-

мости. Величина R сравнивается с порогом

у,

зависящим от объ-

ема выборки

доверительной вероятности. При уровне значимо-

сти 0,05 (доверительной вероятности 0,95) значения порога со-

держатся в

табл.

3.2 [11].

Таблица 3.2

Объем N

Порог

Зависимость порога

0,360

0,328

от объема выборки

0,300

0,276

0,257

Если окажется /? > у, то принимается решение о существен-

ной корреляции элементов остаточного ряда и, следовательно, о

неадекватности модели тренда.

Иногда оказывается целесообразным применение более ком-

плексного критерия, основанного на корреляционной функции

г{т).

Рассчитывается коэффициент

155

где

J< N/3. Доказывается, что статистика

подчинена х^-распре-

делению с (N

—

I) степенями свободы. Тогда если окажется

G < iviooa»

где

iviooa

^сть ЮОа-процентная точка х^-распределения

(А^—

степенями свободы, то

вероятностью

1 —

а элемен-

ты остаточного ряда признаются некоррелированными, а если

они гауссовские, то и независимыми.

Проверка на нормальное распределение остаточного ряда мо-

жет проводиться многочисленными методами, разработанными

в математической статистике. Остановимся на

двух

из них, пола-

гая,

что предыдущие тесты по анализу случайности, центриро-

ванности и независимости дали положительные результаты.

Распространенным методом проверки гипотезы о нормаль-

ном распределении является

'ji^-Kpumepuu

Пирсона.

кратком из-

ложении его существо заключается в следующем.

Пусть

^min

и ^тах соотвстственно наименьший и наибольший

элементы ряда остатков. Отрезок

[е^^^,

^тюА

разбивают на s рав-

ных непересекающихся интервалов так, чтобы в каждый из них

попало не менее пяти элементов ряда. Иногда рекомендуют

1пЛ71п2.

Символами hwNj{j=

1,2,...,

s) обозначены соответ-

ственно длина интервала и число элементов остаточного ряда,

попавших в У-й интервал. Границы у-го интервала обозначены

символамиХу, Xj+ \,Xj =

(xj +

Xj+ \)/2 - центр интервала. Далее под-

считывают теоретические вероятности Pj попадания случайной

величины нау-й интервал:

Pj =h 1 exp'

д/2яа^

2al

строят статистику Пирсона

'P/P_

Затем задаются уровнем значимости а и находят ЮОа-про-

центную точку

vviooa

х^-квадрат распределения

с ^

степенями

свободы. Если окажется

у < wiooa»

то с вероятностью

1 —

а нет ос-

нований отвергать гипотезу о нормальном распределении эле-

156

ментов остаточного ряда; при противоположном неравенстве ги-

потеза отвергается с вероятностью а совершить ошибку.

Более простым, хотя и менее обоснованным, является

метод

асимметрии и

эксцесса.

Его сущность такова [21].

По экспериментальным данным (остаточному ряду) строятся

эмпирические коэффициенты асимметрии

Аа

и эксцесса

Аэ*

л^

^а=-

Кэ='

А:=1

к=\

Если эти коэффициенты близки к

нулю,

то появляются осно-

вания считать остаточный ряд гауссовским. Для усиления этих

оснований вычисляются среднеквадратические отклонения

коэффициентов [И, 21]:

ая =

6(N-l)

(7V+1)(JV + 3)'

24Л^(7У-2)(А^-3)

1(7^-1)^(ЛГ+3)(Л^+5)*

Если

|Аа|

1,5аа,

|Аэ1

»5аэ,

то

считают,

что

распределение ос-

таточного ряда не противоречит гипотезе о нормальном распре-

делении. Если хотя бы один из коэффициентов оказывается

больше двух среднеквадратических отклонений, гипотеза о нор-

мальности отвергается.

Важной характеристикой модели является ее

точность.

Су-

ществуют различные определения этого понятия. Достаточно

распространенной и простой мерой точности является относи-

тельная ошибка

'^отн

1 ^1^-1

=^Sp|ioo;

Если окажется

ЕОТН

^ 15%, то точность признается достаточ-

ной.

Глава

СТОХАСТИЧЕСКИЕ

ВРЕМЕННЫЕ РЯДЫ

4.1.

Случайные процессы

(начальные определения и классификация)

Теория стохастических временных рядов базируется

на

соответ-

ствующей теории случайных (стохастических) процессов. Приве-

дем некоторые исходные положения, полагая, что читатель зна-

ком с терминологией теории вероятностей

элементами вероят-

ностных операций.

Пусть проводится случайный эксперимент и (Q,

Р)

—

соот-

ветствующее

ему

вероятностное пространство, COGQ

элемен-

тарное событие.

Определение

4.1.

Вещественная функция

ф((о) элементар-

ного события

со

называется случайной величиной, если

для

VxG

(—оо,

оо)

множество тех

со,

для которых

ф(со) <

х,

принадлежит

множеству

JF,

т.е.

{со:

ф(со)

x}c

Р(ф(со)е (-оо, оо))

= 1.

Так как для каждого события

из

/^определена вероятность

Р,

то условие

{со:

ф(со)

х}с /"означает, что при любом

может быть

определена вероятность события ф(со) <

х.

Случайная величина,

таким образом, представляет собой величину, значение которой

до проведения эксперимента точно предсказать нельзя, однако

можно указать вероятность того,

что в

эксперименте случайная

величина JSf окажется меньше любого числа

х.

Определение

4.2.

Вещественная функция ДО

ф(со,

О,

где

/е Т

и имеет смысл времени, называется

случайным,

или стохастичес-

ким,

процессом,

если при каждом фиксированном

/ =

Г величина

Х(/*)

ф(о),

является случайной величиной.

Множество Г задает область определения процесса. Сам слу-

чайный процесс, что следует

из

его определения, можно рассма-

тривать как параметрически заданную на множестве ^случайную

величину. Значение случайного процесса

при

фиксированном

аргументе

принято называть

сечением

процесса. Если

экспери-

менте элементарное событие со примет определенное значение

со

co*G Fy

то

функция ф(со

, i)

оказывается детерминированной

158

функцией времени и называется реализацией (траекторией) про-

цесса. Таким образом, случайный процесс как функцию двух пе-

ременных / и со можно рассматривать или как семейство завися-

щих от параметра / случайных величин, или как семейство реали-

заций (содержащее, вообще говоря, бесконечное их число).

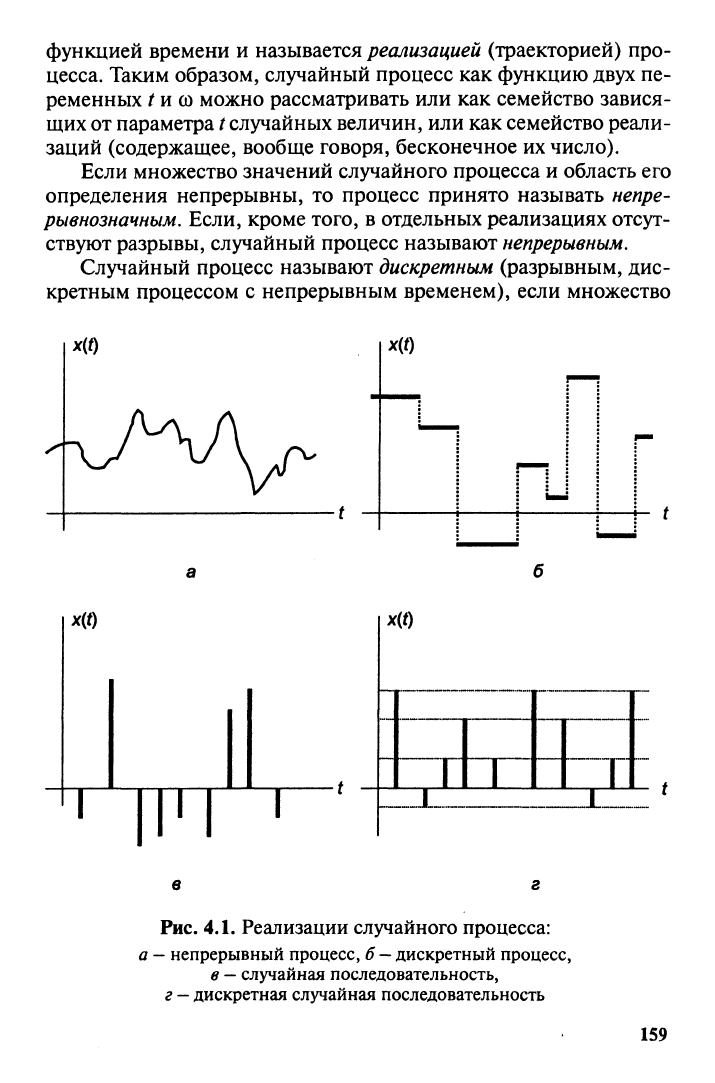
Если множество значений случайного процесса и область его

определения непрерывны, то процесс принято называть непре-

рывнозначным. Если, кроме того, в отдельных реализациях отсут-

ствуют разрывы, случайный процесс называют

непрерывным.

Случайный процесс называют

дискретным

(разрывным, дис-

кретным процессом с непрерывным временем), если множество

x(t)

x{t)

Рис. 4.1. Реализации случайного процесса:

—

непрерывный процесс, б

—

дискретный процесс,

—

случайная последовательность,

—

дискретная случайная последовательность

159