Чикуров Н.Г. Алгоритмическое и программное обеспечение компьютерных систем управления
Подождите немного. Документ загружается.


50
Нас интересует решение задачи в виде системы
дифференциальных уравнений, для которых интегральной кривой
является рассматриваемая окружность.
С этой целью вычислим частные производные:
2; 2; 2;
;;,
xyz
xyz
FFF
FxFyFz
xyz
f FF
fAf BfC
xyz
¶¶¶
¢¢¢
== == ==
¶¶¶
¶¶¶
¢¢¢
== == ==
¶¶¶
и запишем систему линейных уравнений для неявных функций.
0;
0.
xyz
xyz
F F y Fz
f f y fz
¢¢
¢ ¢¢
+ +=
¢¢
¢¢
+ +=
Решение системы дает
;
;
1.
dy Cx Az
y
dx Bz Cy
dz Ay Bx
z
dx Bz Cy
dx
x
dx
-
¢
==
-
-
¢
==
-
¢
==
(2.19)
Заменим в системе (2.19) параметр x на параметр S. Для этого
рассмотрим дифференциал дуги.
()()()
222
.
ds y z x dx
¢¢¢
= ++×
Откуда

51
()()()
( )( )( )
22
222
222
1
.
ds Cx Az Ay Bx
yzx
dx Bz Cy Bz Cy
Cx Az Ay Bx Bz Cy
Bz Cy
æöæö
--
¢¢¢
= + + = + +=
ç÷ç÷
--
èøèø
- +- +-
=
-
Теперь уравнения (2.19) можно записать в следующем виде:
(
)
(
)
( )( )( )( )
( )( )
( )( )( )( )
( )
( )( )( )
222
2 22
2 22
;
;
.
Cx Az Bz Cy
dy dy dx
ds dx ds
Bz Cy Cx Az Ay Bx Bz Cy
Ay Bx Bz Cy
dz dz dx
ds dx ds
Bz Cy Cx Az Ay Bx Bz Cy
Bz Cy
dx dx dx
ds dx ds
Cx Az Ay Bx Bz Cy
--
=×=
- - +- +-
--
=×=
- - += +-
-
=×=
- += +-
Проанализируем выражение под квадратным корнем.
(
)
(
)
(
)
( ) ( ) ( )
2 22
22 22 22 22 22
22 22 22 22 22 22 22
2222 2222 2222
22 2 2 22
22
22
2
222
2222
Cx Az Ay Bx Bz Cy
Cx ACxz Az Ay ABxy Bx Bz
Bcyz cy Ax Ax cz cz By By
ABCx ABCy ABCz
ACxz ABxy Bcyz A x B y c z
R Acxz Acxz ABxy Bcyz A x
-+-+-=
=- ++- ++-
- ++-+-+-=
= ++ + ++ + ++ -
- - - - - -=
=--- --
( ) ( ) ( )
2 22 22
22
2 2222
2.
By cz
R Ax Cz By Ax Cz B y R Ax Cz By R
- -=
=-+ - +- =-++ =
В результате система дифференциальных уравнений
окружности, ориентированной произвольно в пространстве,
принимает вид:

52
( )
( )
( )
,
,
,
dx
Bz Cy
ds
dy
Cx Az
ds
dz
Ay Bx
ds
=j-
=j-
=j-
(2.20)
где
1
R
j=
.
Обозначим:
,
,
.
BzCyF
CxAzG
AyBxH
-=
-=
-=
(2.21)
Тогда дифференциальные уравнения (2.20) примут вид:
,
,
.
dx
F
ds
dy
G
ds
dz
H
ds
=j
=j
=j
Чтобы определить неизвестные
,
FG
и
H
, продифференцируем
уравнения (2.21).
( ) ( ) ( )
( ) ( )
( )
222
1
.
dF dz dy
B C BH CG B Ay Bx C Cx Az
ds ds ds R
ABy B x C x ACZ ABy A x x ACz
AAxByCzxx
=-= -=j -- -=
éù
ëû
=j--+ =j+-+ =
= j + + - = -jéù
ëû
Аналогично:
53
,
.
dG
y
ds
dH
z
ds
= -j
= -j
Окончательно система дифференциальных уравнений
сферической интерполяции принимает вид:
,,
,,
,,
,,
,,
,.
dx
F dx Fds
ds
dy
G dy Gds
ds
dz
H dz Hds
ds
dF
x dF xds
ds
dG
y dG yds
ds
dH
z dH zds
ds
=j =j
=j =j
=j =j
= -j = -j
= -j = -j
= -j = -j
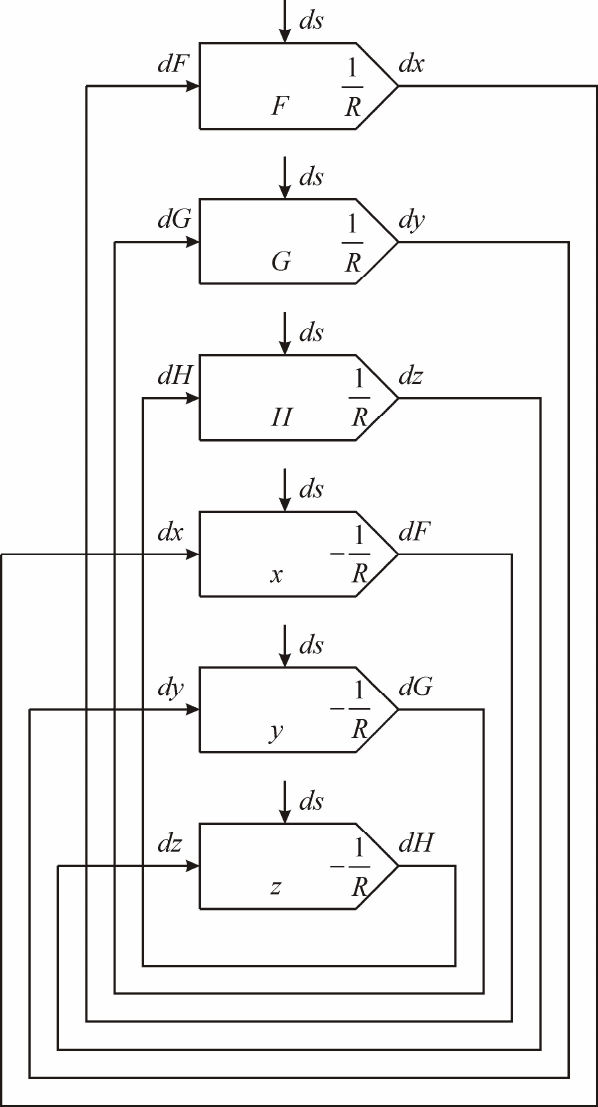
Структурная схема сферического интерполятора включает
шесть интеграторов Римана (рис.2.24).
54
Рис. 2.24. Структурная схема сферического интерполятора
Коэффициенты рядов Тейлора, в которые раскладываются
функции x, y, z, F, G и H, находим по рекуррентным формулам (2.7).
55
10 10 10
21 21 21
32 32 32
43 4 343
, ,,
, ,,
2 22
, ,,
3 33
, ,;
4 44
xF yG zH
xF yG zH
xF yG zH
xF y G zH
=j =j =j
j jj
= ==
j jj
= ==
j jj
= =j=
10 1 0 10
21 2 1 21
32 3 2 32
43 4 3 43
, ,,
, ,,
222
, ,,
333
, ,.
444
Fx Gy Hz
FxGyHz
FxGyHz
FxGyHz
= -j = -j = -j
jjj
=- =- =-
jjj
=- =- =-
jjj
=- =- =-
Значения переменных в конце шага интегрирования находим в
виде степенных рядов, вычисляемых по схеме Горнера.
(
)
{
}
( )
{ }
( )
{ }
43210
43210
43210
,
,
......................................................
.
x xsx sx sx sx
y ysy sy sy sy
H HsH sH sH sH
= D+ D+ D+ D+éù
ëû
= D+ D+ D+ D+éù
ëû
= D+ D+ D+ D+éù
ëû
Перед отработкой кадра управляющей программы в режиме
сферической интерполяции необходимо задать начальные значения
параметров
0 00
,,,
Rxyz
, направляющие косинусы плоскости
интерполяции
,,
ABC
, вычислить начальные значения переменных
000
,
F Bz Cy
=-
0 00
,
G Cx Az
=-
0 00
H Ay Bx
=-
и задать шаг
интегрирования
S
D
. Величина этого шага определяет скорость
движения инструмента по контуру обработки.
56
2.6. Алгоритм сплайновой интерполяции
В инженерной практике многие кривые имеют довольно
сложную форму, не допускающую аналитического задания при
помощи элементарных функций. Поэтому их собирают из
сравнительно простых гладких фрагментов (сегментов), каждый из
которых может быть вполне удовлетворительно представлен в виде
элементарной функции одной переменной.
Для того чтобы получающаяся кривая была достаточно гладкой,
необходимо правильно соединять их в местах стыковки. Для гладкого
изменения касательной вдоль всей составной кривой достаточно
описать стыкуемые кривые при помощи многочленов 3-й степени.
Коэффициенты этих многочленов всегда можно подобрать так, чтобы
соответствующая составная кривая имела непрерывную 2-ю
производную.
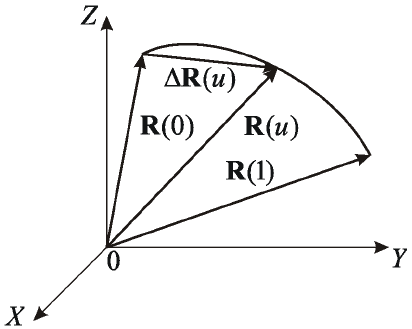
Рассмотрим сегмент кубической параметрической кривой в
форме Фергюсона (рис.2.25), которая описывается векторным
уравнением
32
( ) , 0 1,
uuuuu
= + + + ££
r a b cd
где
u
– параметр:
,,,
abcd
– коэффициенты.
Рис.2.25
Запишем эту систему уравнений в скалярном виде.

57
32
32
32
,
,
.
x x xx
y y yy
z z zz
xau bu cud
yau bu cud
zau bu cud
= + ++
= + ++
= + ++
(2.22)
Продифференцируем уравнения (2.22)
2
2
2
32,
32,
32,
x x xx
y y yy
z z zz
dx
au bucV
du
dy
au bucV
du
dz
au bucV
du
= + +=
= + +=
= + +=
(2.23)
где
2
2
2
32,
32,
32.
x x xx
y y yy
z z zz
V au buc
V au buc
V au buc
= ++
= ++
= ++
(2.24)
Продифференцируем уравнения (2.24).
62,
62,
62,
x
x xx
y
y yy
Z
z zz
dV
au bW
du
dV
au bW
du
dV
au bW
du
= +=
= +=
= +=
(2.25)
где
6 2,
6 2,
6 2.
xxx
yyy
zzz
W aub
W aub
W aub
=+
=+
=+
(2.26)
Продифференцируем уравнения (2.26).
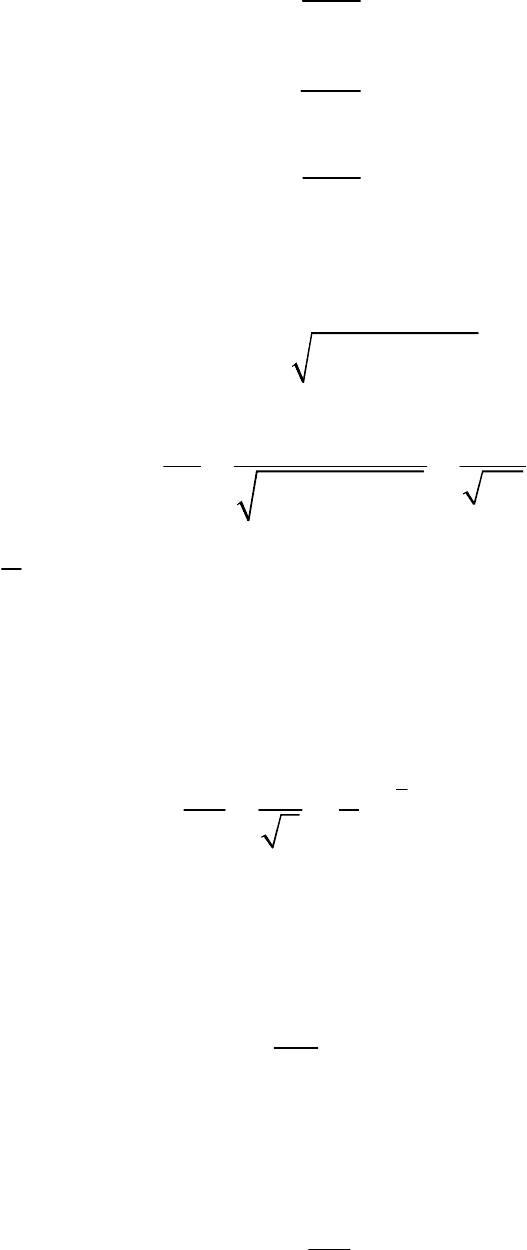
58
6,
6,
6.
x
x
y
y
z
z
dW
a
du
dW
a
du
dW
a
du
=
=
=
(2.27)
Дифференциал дуги сплайна
222
,
xyZ
ds V V V du
= ++
откуда
222
11
,
2
xyz
du
ds
P
VVV
= = =j
++
где
222
1
()
2
xyz
P VVV
= ++ ;
j
– новая переменная.
Найдем производную
j
по
dP
и приравняем ее к новой
переменной
Q
.
3
3
2
11
().
2
2
d
PQ
dP
-
j
= - =-j=
(2.28)
Найдем производную
Q
по
d
j
и приравняем ее к новой
переменной
R
.
2
3.
dQ
R
d
=-j=
j
(2.29)
Найдем производную
R
по
d
j
.
6.
dR
d
=-j
j
(2.30)

59
Продифференцируем сложную функцию
(
)
PVu
éù
ëû
по
переменной
u
.
1
.
2
yy
xx
zz
xyz
xyz
dV dV
dV dV
dV dV
dPPPP
VVV
du V du V du V du du du du
æö
¶¶¶
= + + =++
ç÷
ç÷
¶¶¶
èø
(2.31)
На основе уравнений (2.23), (2.25), (2.27), (2.28), (2.29), (2.30),
(2.31), составляем систему дифференциальных уравнений в форме
Шеннона, описывающую алгоритм сплайновой интерполяции [12].
,
,
,
,
,
,
,
6,
6,
6,
,
,
6,
,
,
,
.
x
y
z
xx
yy
zz
xx
yy
zz
xyz
x xx
y yy
z zz
du ds
dx V du
dy V du
dz V du
dV W du
dV W du
dV W du
dW a du
dW a du
dW a du
d QdP
dQ Rd
dRd
dP dP dP dP
dP V dV
dP V dV
dP V dV
=j
=
=
=
=
=
=
=
=
=
j=
=j
=-jj
=++
=
=
=
(2.32)
Систему уравнений (2.32) можно представить в виде схемы
соединений интеграторов Стилтьеса и Римана (рис. 2.26). Каждому
уравнению системы (2.32) отвечает определенный интегратор.
