Чикуров Н.Г. Алгоритмическое и программное обеспечение компьютерных систем управления
Подождите немного. Документ загружается.

40
или
() () .
dx t u t dt
=
(2.1)
Проинтегрируем уравнение (1) с помощью интеграла Римана:
0
()
t
x(t) u t dt
=
ò
, (2.2)
где t - независимая переменная.
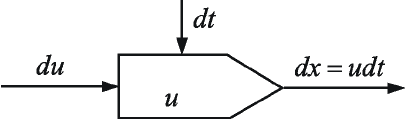
Для интегрирования применим специальное устройство –
интегратор (рис.2.13).
Рис.2.13. Интегратор (условное изображение)
Таким интегратором может служить операционный усилитель.
Предположим, что подынтегральная функция u(t) задана в виде
степенного ряда:
23
0123
(),
ut u utut ut= +D+D+D+
K
(2.3)
где
012
,,,
uuu
K
- коэффициенты ряда.
Требуется найти коэффициенты степенного ряда переменной
x(t) на выходе интегратора:
23
0123
(),
xt x xt xt xt= +D+D+D+
K
(2.4)
где
012
,,,
xxx
K
- коэффициенты ряда.
Для решения задачи продифференцируем выражение (2.4).
2
123
(23)
dx x x t x t dt
= + D+ D+
K
, (2.5)
но
23
0123
()
dx udt U U t U t U t dt
= = + D+ D+ D+
K
. (2.6)
41
Приравнивая в (2.5) и (2.6) коэффициенты при одинаковых
степенях получаем
10
21
32
43
,
1
,
2
1
,
3
1
,
4
xu
xu
xu
xu
=
=
=
=
LLLL
(2.7)
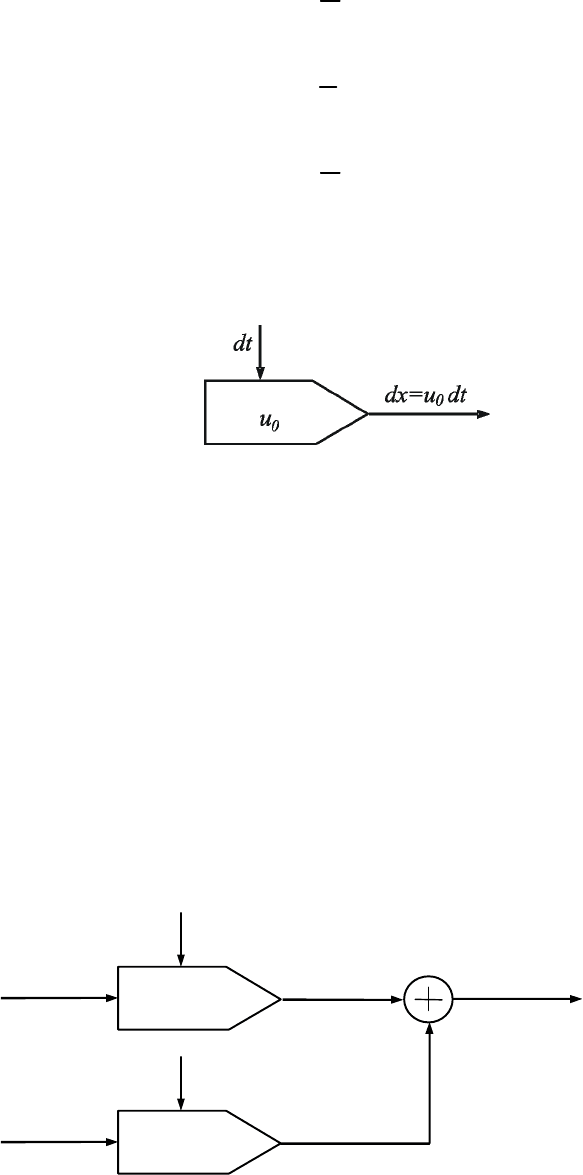
В частном случае, при
0
const
uu
==
, интегратор изменяется
(рис.2.14).
Рис.2.14. Интегратор при u=u
0
=const.
Рекуррентные формулы для вычисления коэффициентов
степенных рядов принимают следующий вид:
10
2
3
4
,
0,
0,
0,
xu
x
x
x
=
=
=
=
LLL
(2.8)
Рассмотрим параллельное соединение звеньев (рис.2.15)
Рис.2.15. Параллельное соединение интеграторов
dt
du
dx
u
dt
dv
dy
y
dz=dx+dy

42
Данной схеме соответствуют рекуррентные формулы для
вычисления коэффициентов степенных рядов вида:
111 00
222 11
3 33 22
444 33
,
1
( ),
2
1
( ),
3
1
( ),
4
zxyuv
z x y uv
zxy uv
z x y uv
=+=+
=+=+
=+=+
=+=+
LLLLLLLLLLL
(2.9)
2) Интеграл Стилтьеса
Рассмотрим дифференциальное уравнение
()
( ),
()
dxs
us
dst
=
или
() () ().
dxs usdst
=
(2.10)
Проинтегрируем уравнение (2.10) по Стилтьесу.
0
() ()
s
x(s) usdst
=
ò
, (2.11)
где
()
us
- подынтегральная функция; ds(t) – интегрирующая сложная
функция, зависящая от t.
Для интегрирования применим интегратор Стилтьеса (рис.2.16).
Рис.2.16. Интегратор (условное изображение).
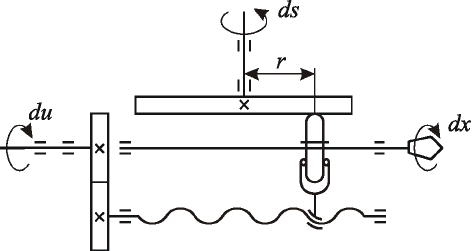
43
Моделью такого интегратора может служить механическое
решающее устройство (рис. 2.17).
Рис.2.17. Интегратор Стилтьеса
Заданы степенные функции:
23
0123
23
0123
...
...
s s stst st
uu utut ut
ì
= +D+D+D+
í
= +D+D+D+
î
(2.12)
Требуется найти коэффициенты степенного ряда:
23
0123
()xt x xt xt xt
= +D+D+D+
K
(2.13)
Решаем задачу. Продифференцируем уравнения (2.12) и (2.13).
2
123
2
123
( 2 3 ...)
,
( 2 3 ...)
ds s s t s t dt
dx x x t x t dt
ì
= + D+ D+
í
=+D+D+
î
(2.14)
но
232
0123 123
( ...)( 2 3 ...)
dx uds u u t u t u t s s t s t dt
= = +D+D+D+ + D+ D+ (2.15)
Для облегчения вычислений выражение (2.15) можно записать в
виде:
44
Из соотношения (2.15) получаем:
1 01
2 0 2 11
3 03 12 21
4 04 13 22 31
,
1
(2 ),
2
1
(3 2 ),
3
1
(432)
4
x us
x us us
x us us us
x us us us us
=
=+
= ++
= +++
LLLLLLLLLLLLLL
(2.16)
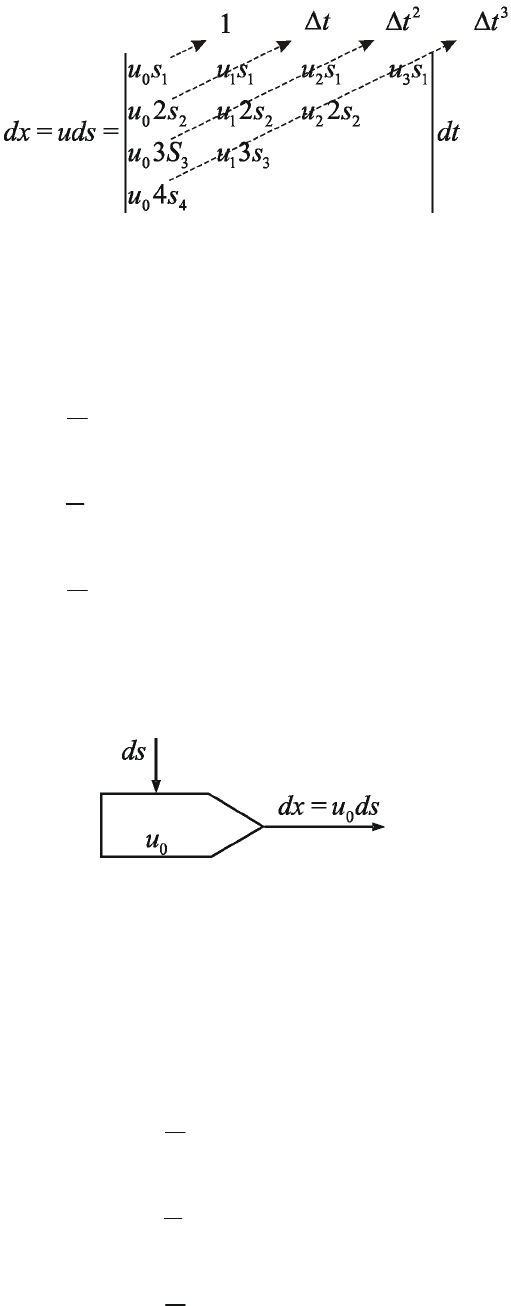
В частном случае, при u=u
0
=const, интегратор изменяется
(рис.2.18)
Рис.2.18. Интегратор при u=u
0
=const.
Рекуррентные формулы для вычисления коэффициентов
степенного ряда принимают следующий вид:
1 01
2 02 02
3 03 03
4 04 04
,
1
2,
2
1
3,
3
1
4,
4
x us
x us us
x us us
x us us
=
==
==
==
LLLLLLLL
(2.17)

45
При параллельном соединении звеньев (рис.2.19) формулы для
вычисления коэффициентов степенного ряда определяются как
суммы коэффициентов, найденные для каждого интегратора в
отдельности.
Рис.2.19. Параллельное соединение интеграторов.
1 01 01
2 02 11 0 2 11
3 03 12 21 03 12 21
4 04 13 22 31 0 4 13 22 31
,
1
(2 2 ),
2
1
(3 2 3 2 ),
3
1
(4 3 2 4 3 2 ),
4
z us vq
z u s us v q vq
z us us us vq vq vq
z us us us us vq vq vq vq
=+
= +++
= +++++
= +++++++
LLLLLLLLLLLLLLLLLLLLLLLLLL
(2.18)
Рассмотрим примеры решения систем дифференциальных
уравнений степенным методом.
Круговая интерполяция
Запишем уравнение окружности
в параметрической форме (рис.2.20).
sin,
cos.
yR
xR
=a
ì
í
=a
î
Рис.2.20 Круговая интерполяция
ds
du
dx
u
dq
dv
dy
v
dz=dx+dy
d
a
0
x
y
R
ds
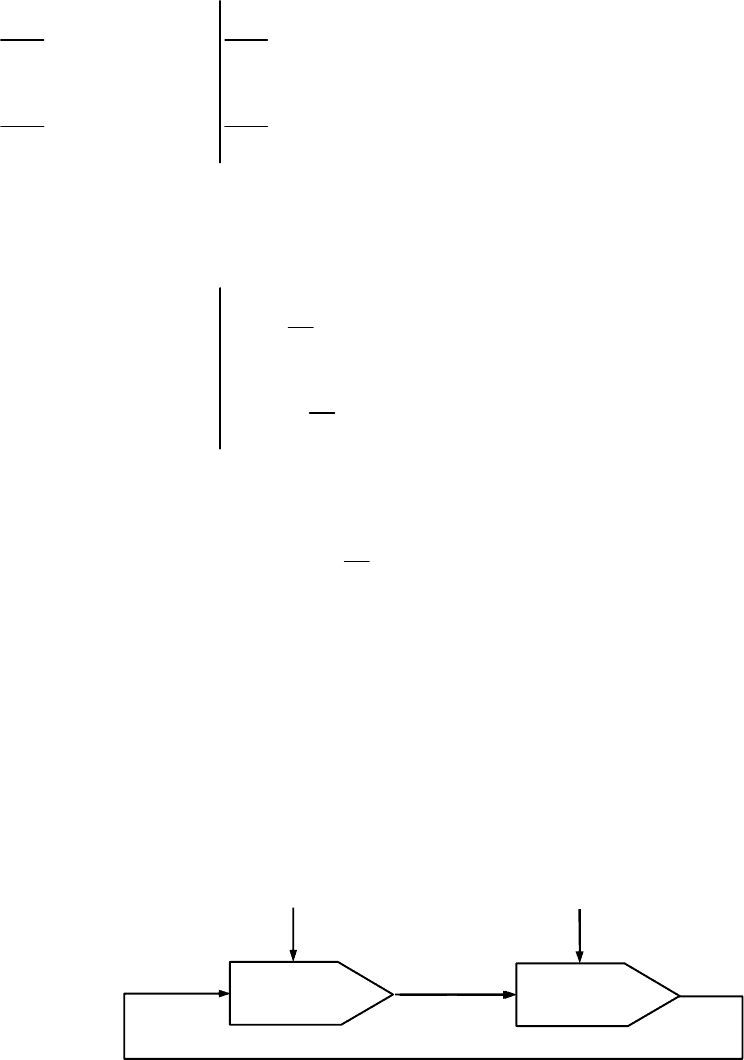
46
Продифференцируем эти уравнения.
cos,,
sin,,
dy dy
Rx
dd
dx dx
Ry
dd
ì
=a=
ï
ï
aa
í
ï
=- a =-
ï
aa
î
Теперь запишем их в форме Шеннона.
1
,
,
,1
,
dy xds
dy xd
R
dx yd
dx yds
R
ì
=
ï
=a
ï
í
=-a
ï
=-
ï
î
где ds=Rda.
Обозначим для краткости
1
R
=j
. Тогда:
,
, const.
dy xds
dx yds
=j
ì
í
=-j j=
î
Двум дифференциальным уравнениям соответствуют два
последовательно включенные интегратора (рис.2.21).
Рис.2.21. Схема соединения интеграторов при круговой интерполяции
Применяя для полученной схемы уравнения (2.7), записываем
рекуррентные формулы, с помощью которых будут вычисляться
коэффициенты степенных функций
()
xt
и
()
yt
.
ds
dy dx
y
ds
dx
x
j
-
j

47
1 0 10
2 1 21
3 2 32
4 3 43
,,
11
,,
22
11
,,
33
11
,,
44
x y yx
x y yx
x y yx
x y yx
=-j =j
=-j =j
=-j =j
=-j =j
LLLLL LLLLL
Абсолютные значения координат находим по схеме Горнера:
43210
43210
{[( ) ]}
{[( ) ]}
x xsx sx sx sx
y ysy sy sy sy
= D+ D+ D+ D+
ì
í
= D+ D+ D+ D+
î
Воспроизведение гиперболы
Запишем уравнение гиперболы.
1
0
0
11
( ).
()
y tt
kttk
-
= =+
+
Продифференцируем его.
22
0
2
0
11
().
()
dy
t t ky
dt k ktt
-
=- + =- =-
+
С помощью замены переменных запишем данное уравнение в
форме Шеннона.
2
,
,
2
2.
dy
dy dt
kyz
dt
dz
ky
dz kydy
dt
ì
=
=-=
ï
ï
í
ï
=-
=-
ï
î
48
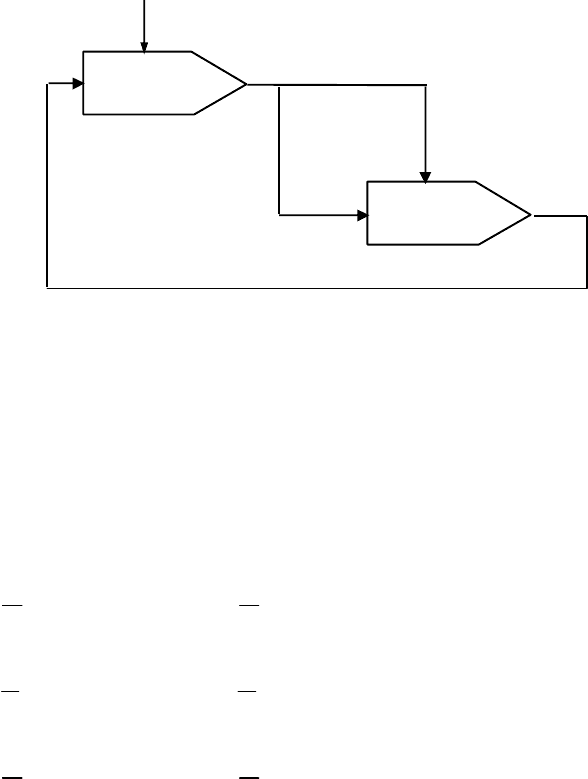
Двум дифференциальным уравнениям соответствует схема из
двух интеграторов (рис.2.22).
Рис. 2.22. Схема для воспроизведения гиперболы
С помощью рекуррентных формул (2.7) и (2.16) вычисляем
коэффициенты степенных рядов, аппроксимирующих функции
()
yt
и
()
zt
.
1 0 1 01
2 1 2 0 2 11
3 2 3 03 12 21
4 3 4 04 13 22 31
, 2,
11
, 2 (2 ),
22
11
, 2 (3 2 ),
33
11
, 2 (4 3 2 ),
44
y z z kyy
y z z k yy yy
y z z k yy yy yy
y z z k yy yy yy yy
= =-
= =-+
= =- ++
= =- +++
LLLLL LLLLL
Приближенные значения функций вычисляем, как и ранее, в
виде схемы Горнера.
43210
43210
{[( )]},
{[( )]}.
y ysy sy sy sy
z zsz sz sz sz
= D+ D+ D+ D+
ì
í
= D+ D+ D+ D+
î
2.5. Алгоритм сферической интерполяции
Алгоритм сферической интерполяции [9], [12] может
применяться для управления обработкой сложнопрофильных деталей
на металлорежущих станках фрезерной группы, а также на
dz
dy
y
dt
dz
z
-2k
dy
49
многокоординатных станках. Кроме того, этот алгоритм удобен для
управления промышленными роботами, рабочие органы которых
перемещаются по сложным пространственным траекториям.
Сущность сферической интерполяции сводится к
воспроизведению на станке или в роботе дуг окружностей,
ориентированных произвольно в пространстве. Соединяя участки дуг
разных радиусов, и ориентируя в пространстве плоскости, в которых
расположены эти дуги соответствующим образом, можно достаточно
точно аппроксимировать разнообразные кривые, по которым
движется режущий инструмент или рука робота. Важно, что при
таком способе аппроксимации кривых, первая производная на
границе смежных участков не терпит разрыва, т.е.
аппроксимирующая функция гладкая.
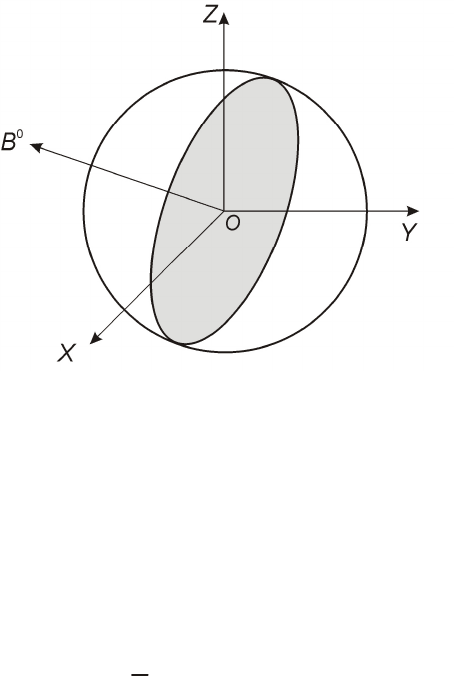
Чтобы вывести алгоритм сферической интерполяции,
рассмотрим в пространстве дугу окружности (рис.2.23). Чтобы ее
получить, рассечем сферу с центром в начале координат плоскостью,
проходящей также через начало координат и ориентированной в
пространстве определенным образом.
Рис.2.23
Решаем совместно уравнение сферы и уравнение центральной
плоскости.
2222
(,,)0
( , , ) 0,
x y z R Fxyz
Ax By Cz f xyz
++-==
++==
где
R
– радиус сферы; A, B, C. – направляющие косинусы
единичного вектора нормали
0
B
к плоскости.
