Чикуров Н.Г. Алгоритмическое и программное обеспечение компьютерных систем управления
Подождите немного. Документ загружается.

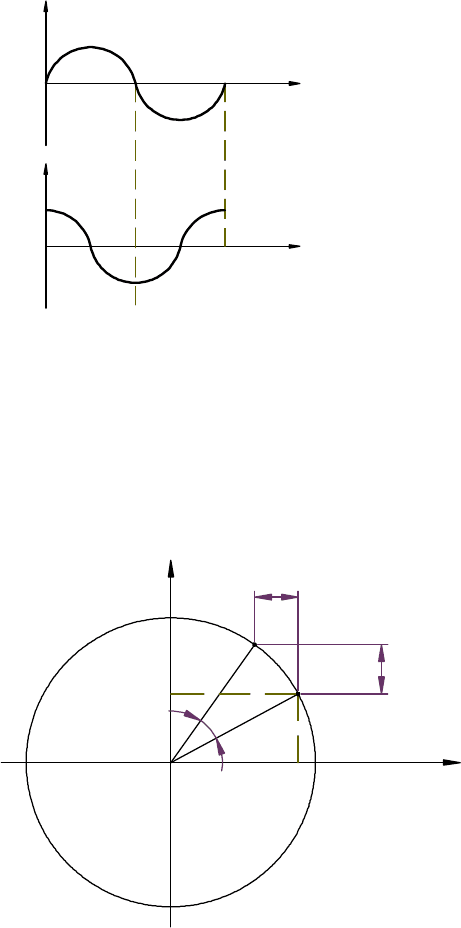
30
y
V
x
V
0
0
t
t
Рис.2.4. Изменение скоростей при круговой интерполяции
В результате ортогонального суммирования скоростей
результирующее движение осуществляется по дуге окружности
(рис.2.5).
i
X
i
Y
Y
1
i
X
+
D
1
i
Y
+
D
X
h
Рис.2.5. Круговая интерполяция:
h
– шаг интерполяции (шаг
интегрирования),
,
ii
XY
– координаты текущей точки окружности,
11
,
ii
XY
++
DD
– приращение координат
Приращения координат в режиме круговой интерполяции
рассчитываются по формуле
1
1
,
,
i iс is
i iс is
x xh yh
y yh xh
+
+
D=+
D=-
31
где
3
sin(),
6
S
h
h hh= »-
24
cos()1
2 24
С
hh
hh
= -»-+
.
Далее рассчитываются новые значения координат:
11 ++
D
+
=
D
iii
xxx ;
11 ++
D
+
=
D
iii
yyy .
В технологически сложных задачах в процесс интерполяции
может быть вовлечено от 5 до 6 управляющих координат (рис.2.6).
1 11
(,,)
oxyz
1 11
(,,)
oxyz
1 11
(,,)
oxyz
L
L
L
N
N
N
M
M
M
(,,)
xyz
(,,)
xyz
(,,)
xyz
а б в
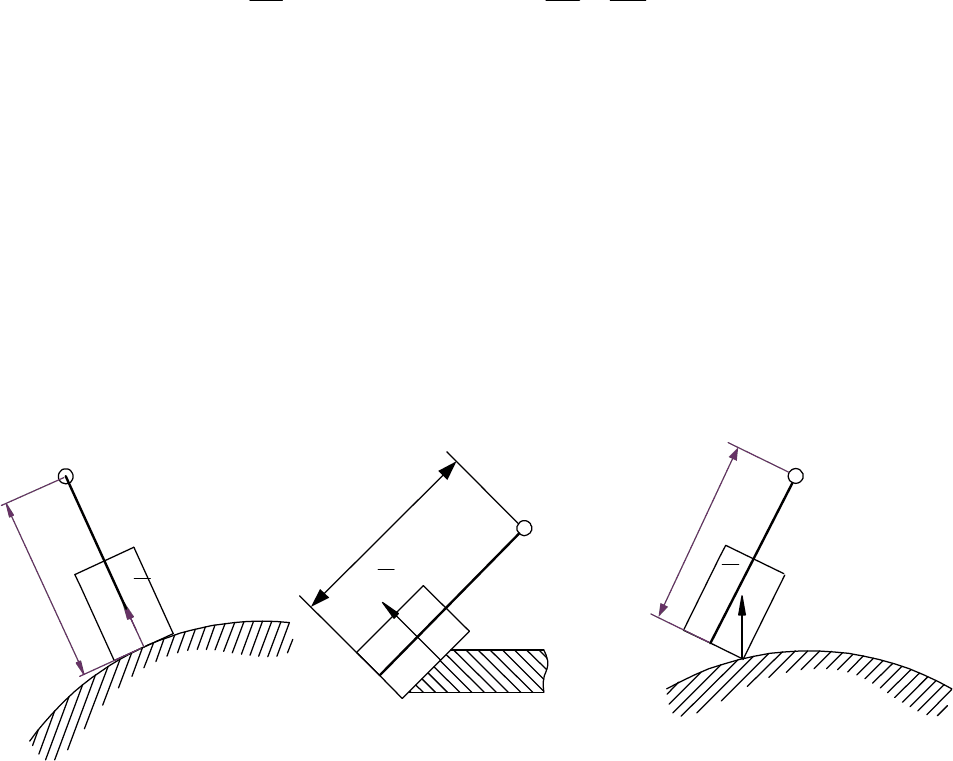
Рис.2.6. Основные виды 5-координатной обработки: а - обработка
торцом фрезы, б - обработка периферией фрезы, в - обработка
торцовой частью фрезы, М(X,Y,Z) – точка контура обработки,
М(X
1
,Y
1
,Z
1
) – точка поворота инструмента
Для реализации многокоординатного формообразования к трем
основным приводам подачи в декартовой координатной системе
должны быть добавлены приводы подач поворотных фрезерных
головок, столов и т.п. (рис.2.7, рис.2.8).
32
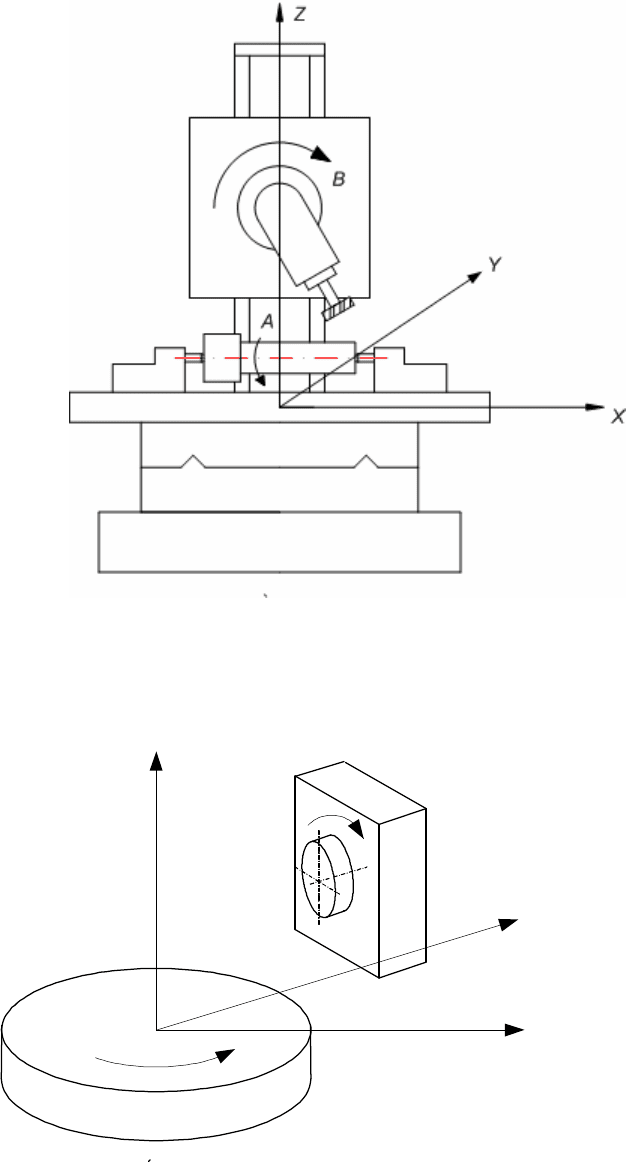
Рис.2.7. Компоновка 5-координатного станка
X
Y
B
C
Z
0
Рис. 2.8.Поворотный стол с вертикальной осью вращения
33
2.2. Применение численных методов решения
обыкновенных дифференциальных уравнений в
системах ЧПУ
Методика воспроизведения различных траекторий на
металлорежущих станках, основанная на численном решении систем
дифференциальных уравнений, универсальна и может применяться
при проектировании современных систем ЧПУ класса ICNC [10].
Выбирая в системе дифференциальных уравнений в качестве
независимого параметра приращение вдоль дуги ∆S, можно
стабилизировать скорость движения инструмента относительно
детали или изменять ее по заранее заданному закону.
В зависимости от цели управления в системах
дифференциальных уравнений может быть выбрана иная
параметризация – либо на основании сведений о требуемых
динамических характеристиках процесса управления (внутри
системы управления), либо на основании сигналов обратной связи,
поступающих с управляемого объекта. Например, задавая в системе
дифференциальных уравнений в качестве независимого параметра
ускорение, можно управлять процессом разгона и торможения
некоторого рабочего органа с заданной функцией ускорения или
замедления. При управлении технологическим процессом резания
таким способом можно регулировать в реальном масштабе времени
силу или скорость резания и т. п.
Обратимся теперь к анализу численных методов, которые
можно использовать для решения дифференциальных уравнений в
системах ЧПУ класса ICNC.
В прежних устройствах ЧПУ, выполненных на основе цифровых
дифференциальных анализаторов (ЦДА), интегрирование
дифференциальных уравнений осуществлялось, как правило, методом
Эйлера. Это наиболее простой и в то же время наименее точный
метод. Требуемая точность вычислений в таких устройствах ЧПУ
достигалось за счет выбора чрезвычайно малого шага
интегрирования. Тактовая частота суммирования приращений в ЦДА
находится в мегагерцовом диапазоне. Ясно, что в компьютерных
системах ЧПУ применять метод Эйлера для расчета сложных
траекторий нерационально.
34
Для этой цели более подходят методы типа Рунге-Кутты.
Исследуем погрешность метода Рунге-Кутты 4-го порядка на простом
примере линейной системы дифференциальных уравнений,
описывающих движение инструмента по дуге окружности.
В табл. 2.1 представлены значения ошибок, накопленных в
процессе решения этих уравнений на длине всей окружности.
Вычисления производились для трех диаметров при пяти значениях
контурной скорости. Из таблицы видно, что на рабочих подачах (для
обычной фрезерной обработки V≤1,5 м/мин) накопленная
погрешность не превышает допустимого значения, равного 1 мкм
(цена дискреты отсчета перемещений в современных компьютерных
СЧПУ).
При высокоскоростной обработке, когда контурная скорость
рабочей подачи может составлять 6 и более метров в минуту,
погрешность решения задачи превышает допустимую величину, если
диаметр обрабатываемого контура мал (D ≤ 5 мм).
На ускоренных же подачах, которые в современных станках
достигают 60–90 м/мин., погрешность решения дифференциальных
уравнений окружности не укладывается в заданную норму точности.
При движении по дуге окружности диаметром D = 50 мм со
скоростью 60 м/мин погрешность составляет 29 мкм.
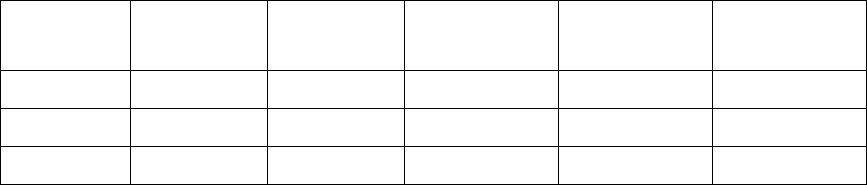
Т а б л и ц а 2.1
Накопленная ошибка в конечной точке окружности, мкм
Контурная
скорость
V, м/мин
0.75 1.5 3.0 6.0 60
D=500 мм
3x10
-9
2x10
-8
2x10
-7
3x10
-6
3x10
-2
D=50 мм
7x10
-7
1x10
-5
2x10
-4
3x10
-3
29
D=5 мм
7x10
-4
1x10
-2
2x10
-1
3 680
Вместе с тем именно с использованием режимов круговой и
сплайновой интерполяций выгодно осуществлять высокоточные
ускоренные перемещения рабочих органов металлорежущих станков.
Благодаря плавному характеру траекторий, построенных при
помощи сегментов окружностей или сплайн-функций, можно
существенно повысить скорости холостых ходов и обеспечить
мягкую, безударную работу металлорежущих станков.

35
Интегрирование дифференциальных уравнений осуществляют с
фиксированным шагом. Шаг интегрирования для дуги окружности
вычисляется по формуле
,
60
FT
h
R
×
=
×
где F – контурная скорость подачи, мм/мин; T – период таймерных
прерываний, с; R – радиус окружности, мм.
Период таймерных прерываний принимают равным T = 10 мс.
Указанное значение периода прерываний программ интерполяции в
системах ЧПУ класса ICNC в настоящее время можно считать
оптимальным. Увеличение этого значения больше 10 мс связано с
нежелательным увеличением шага интегрирования, а уменьшение
менее 10 мс приводит к серьезным трудностям при обслуживании
частых прерываний в операционной системе Windows NT, а также к
снижению производительности вычислений.
Чтобы накопленная ошибка вычислений не превосходила одной
дискреты, значения дискретизации по времени (периоды таймерных
прерываний T) не должны превышать значений, указанных в
табл. 2.2.
Т а б л и ц а 2.2
Требуемая дискретизация по времени для режима
круговой интерполяции
Окружность D=500 мм D=50 мм D=5 мм
Dt, mc
15 3 0.6
Обобщая изложенное, можно сделать следующее заключение:
для численного интегрирования дифференциальных уравнений
окружностей и сплайн-функций применительно к системам ЧПУ
класса ICNC необходимы численные методы с порядком выше 4-го.
2.3 .Дифференциальные уравнения в форме Шеннона
Английским математиком К. Шенноном [21] приводится
доказательство теоремы, согласно которой систему обыкновенных
дифференциальных уравнений, не содержащую
гипертрансцендентные функции, можно решить с применением
36
только интеграторов и сумматоров, если эти уравнения записать в
виде:
00
nn
k kijij
ij
dy a y dy
==
=
åå
(
)
(
)
nkyxy
kk
,...,3,2,
00
=
=
,
где
0
1
y
=
(введено для компактности записи);
1
yx
=
– независимая
переменная;
2
,...,
n
yy
– зависимые переменные.
Уравнения Шеннона отличаются тем, что содержат лишь
операции умножения и суммирования. Отсутствие функциональных
преобразований позволяет упростить и унифицировать процесс
численного интегрирования дифференциальных уравнений в форме
Шеннона. Для этого, как будет показано ниже, достаточно в
исходных уравнениях, заданных в нормальной форме Коши,
произвести простую замену переменных.
В отличие от уравнений в форме Коши в уравнениях Шеннона
отсутствует общий для всех уравнений множитель
dx
,
представляющий собой дифференциал независимой переменной. Это
означает, что уравнения Шеннона требуют интегрирования не по
Риману, а по Стилтьесу. Для этой цели необходимы специальные
формулы численного интегрирования по Стилтьесу, которые будут
рассмотрены далее.
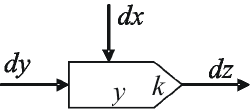
Интегратор Стилтьеса принято изображать в виде
ориентированного пятиугольника (рис. 2.9).
Рис. 2.9. Изображение интегратора Стилтьеса
Интегратор решает интеграл Стилтьеса
() ()
,
b
a
z ytdxt
=
ò
где
(
)
ty – подынтегральная функция;
(
)
xt
– интегрирующая
функция;
t
– независимый аргумент.

37
К уравнениям Шеннона можно привести рациональные,
алгебраические и трансцендентные функции. Исключение
составляют лишь довольно редко встречающиеся
гипертрасцедентные (трансцедентно-трансцедентные) функции,
например гамма – функция или дзета-функция Римана.
Покажем на нескольких простых примерах методику записи
дифференциальных уравнений в форме Шеннона.
1) Воспроизведение экспоненциальной функции
kx
ye
=
Первая производная этой функции
kx
dy
ke
dx
= ,
то есть она равна
.
dy
ky
dx
=
Дифференциальное уравнение в форме Шеннона имеет вид:
(
)
00
, .
dy kydx y x y
==
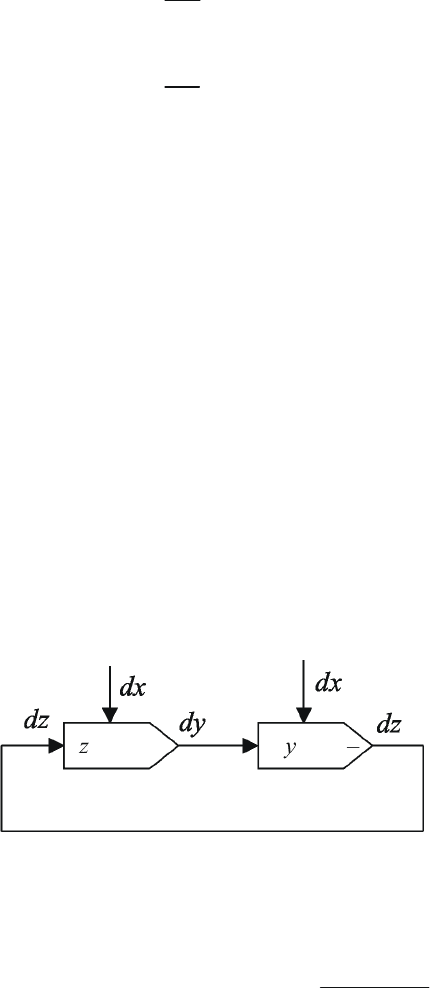
Структурная схема вычислительного устройства состоит только
из одного интегратора, охваченного обратной связью (рис. 2.10).
Рис. 2.10 Схема вычисления функции
kx
ye
=
На вход интегратора поступают приращения функции. В
результате интегрирования по независимой переменной x на выходе
интегратора образуются приращения этой же функции (
dy kydx
=
).
Эти приращения по цепи обратной связи поступают на вход этого же
интегратора.
Интегрирующей функцией в данном интеграторе служит
независимая переменная
x
, значит, это интегратор Римана, который
следует рассматривать как частный случай интегратора Стилтьеса.
38
2) Воспроизведение тригонометрической функции
sin
yx
=
Получение этой функции сводится к решению системы
дифференциальных уравнений
.
dy
z
dx
dz
y
dx
ì
=
ï
ï
í
ï
=-
ï
î
В форме Шеннона система принимает вид:
.
dy zdx
dz ydx
=
ì
í
=-
î
(
)
()
00
00
yxy
zxz
=
=
Структурная схема, соответствующая уравнениям Шеннона,
состоит из двух последовательно соединенных интеграторов Римана
(рис. 2.11). Наряду с функцией
sin
yx
=
в рассматриваемой схеме
вычисляется функция
cos
zx
=
.
Рис. 2.11 Схема вычисления
sin
yx
=
3) Воспроизведение гиперболы
( )
0
1
y
ktt
=
+
Продифференцируем эту функцию по
t
и введем новую
переменную
z
, которую, в свою очередь, продифференцируем по
y
.
39
2
.
2
dy
kyz
dt
dz
ky
dy
ì
=-=
ï
ï
í
ï
=-
ï
î
Запишем полученную систему дифференциальных уравнений в
стандартной форме Шеннона.
.
2
dy zdt
dz kydy
=
ì
í
=-
î
(
)
(
)
.;
0000
ztzyty
=
=
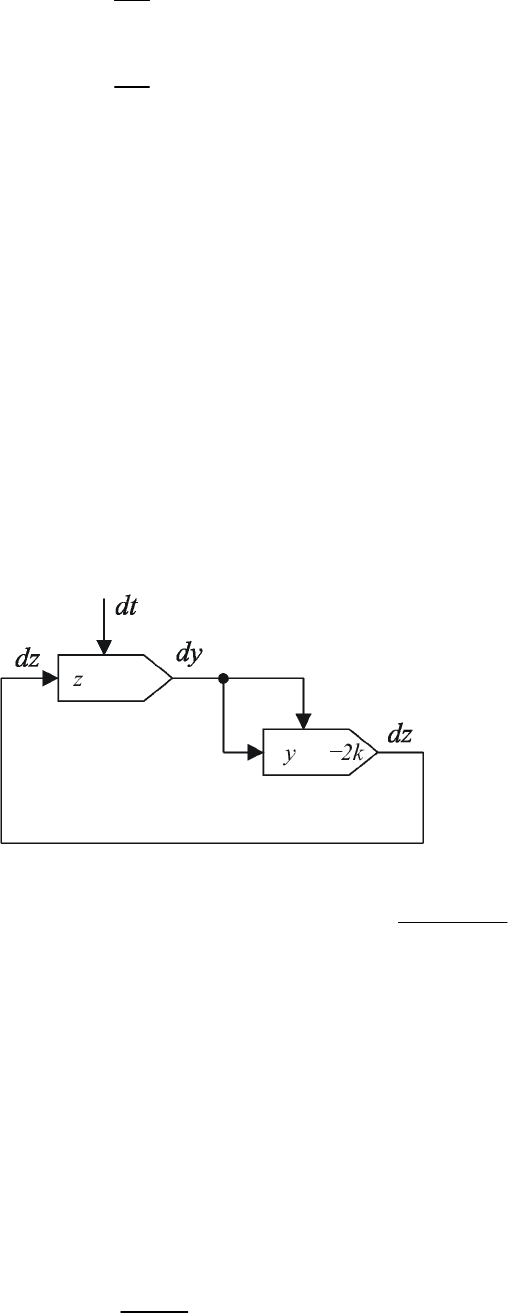
На основании уравнений Шеннона строим структурную схему
вычислительного устройства (рис. 2.12). Схема содержит один
интегратор Стилтьеса.
Рис. 2.12 Схема вычисления функции
( )
0
1
y
ktt
=
+
2.4. Решение дифференциальных уравнений в форме
Шеннона с помощью степенных рядов [12]
1) Интеграл Римана (частный случай интеграла Стилтьеса)
Рассмотрим дифференциальное уравнение
()
( ),
dxt
ut
dt
=
