Черняк О.І. та ін. Економетрика
Подождите немного. Документ загружается.

117
Рис. 4.1. Модель споживання залежно від доходів
Очевидно, що використання звичайного методу найменших квадратів не буде
оптимальним, адже не виконуються умови теореми Гаусса – Маркова. Можна показати,
що у випадку гетероскедастичності збурень
оцінки МНК будуть незміщеними, але не
будуть ефективними (не матимуть найменшої дисперсії)
. Таким чином, має
існувати метод для оцінювання регресії з кращими характеристиками.
Крім цього, можна показати, що стандартні оцінки коварiацiйної матриці оцінювання
МНК будуть зміщеними i, як наслідок, процедури перевірки гіпотез та інтервального
оцінювання, основані на стандартних статистиках, будуть некоректними. Іншими
словами, використання звичайного МНК для розглянутої моделі призведе до некоректної
перевірки статистичних гіпотез.
4.2. Зважений метод найменших квадратів у випадку відомої коваріаційної
матриці збурень
Припустимо, що коваріаційна матриця збурень відома з точністю до коефіцієнта
пропорційності, тобто
22
D
tt
vw, 1,tn ,
де
2
t
w відомі, а
2
– невідомий коефіцієнт пропорційності.
У моделі (4.1) почленно розділимо t -те рівняння на
t
w
(
1,
)
tn
:
** * *
00 11 -1,-1
,1,
tt t ktkt
y
xx x tn , (4.2)
де
*
,1,
t
t
t
y
y
tn
w
;
*
0
1
t
j
x
w
,
*
,1,1,1,
tj
tj
j
x
x
j
ktn
w
; ,1,
t
t
t
v
tn
w
.
Теорема 4.1. Збурення моделі (4.2) відповідають умовам теореми Гаусса – Маркова.
Доведення. Покажемо, що нові збурення ,1,
t
t
t
v
tn
w
повністю задовольнять
класичним властивостям. Спочатку обчислимо математичне сподівання:
M
MM 0
tt
t
tt
ww
.
Дисперсія збурень
2
22222
222
111
DM M M D .
t
tt t t t
t
ttt
v
vvw
w
www
Крім того, коваріація збурень
11
cov
(
,
)
MM M cov
(
,
)
0.
tj
tj tj tj tj
tj tj tj
vv
vv v v
ww ww ww
Таким чином, збурення моделі (4.2) відповідають умовам теореми Гаусса – Маркова.
З доведеної теореми випливає, що отримана модель (4.2) є моделлю класичної лінійної
регресії. Оцінки вектора параметрів регресії
ˆ
, знайдені в моделі методом найменших
квадратів, мають необхідні статистичні властивості, тобто задовольняють теоремі
Гаусса – Маркова, а головне, цими оцінками можна користуватись для статистичних
висновків.
Таким чином,
оцінкою зваженого МНК коефіцієнтів моделі з гетероскедастичними
збуреннями називається оцінка звичайного МНК, знайдена за моделлю (4.2).
На практиці найчастіше значення
t
w
невідомі. Якщо не робити додаткових
припущень, то їх оцінити неможливо, тому що їхня кількість дорівнює кількості
спостережень. Існує кілька способів, що дозволяються обрахувати величини
t
w на
практиці.
Зауваження. Спроможну у випадку гетероскедастичності оцінку коваріаційної
матриці запропонував Х. Уайт:
118
11
ˆ
D,
TTT
β XX X XXX
(4.3)
де діагональна матриця,
t
-й діагональний елемент якої дорівнює
ˆ
t
, де
ˆ
t
– залишки
найменших квадратів. Єдиною додатковою умовою для спроможності й асимптотичної
нормальності порівняно з класичною моделлю є умова обмеженості всіх
2
t
. Оцінки
доступного зваженого МНК будуть асимптотично еквівалентними оцінкам звичайного
МНК у випадку, якщо відомі вагові коефіцієнти, лише за наявності спроможних оцінок
останніх. Ця умова також необхідна для коректності оцінювання коваріаційної матриці
(звичайно, в асимптотичному розумінні; про можливість точного оцінювання не йдеться).
Отже, у випадку, коли дослідник не впевнений у характері
гетероскедастичності,
перевагу слід віддати звичайному методу найменших квадратів. Гіпотези треба
перевіряти звичайним чином, але у відповідних формулах стандартну оцінку
коваріаційної матриці слід замінити на оцінку (4.3). Зазначимо, що в останні роки цей
підхід починає переважати в практичних дослідженнях.
4.3. Виявлення гетероскедастичності
Дуже часто виникнення проблеми гетероскедастичності можна передбачити
заздалегідь, базуючись на знаннях про характер даних, що їх використовують у регресії.
У таких випадках можна вжити відповідних заходів для усунення цього ефекту на етапі
специфікації моделі регресії, і це дозволить зменшити або, можливо, усунути необхідність
формальної перевірки.
На сьогодні не існує загальноприйнятого способу
виявлення гетерескедастичності,
проте, розроблено кілька критеріїв, які можна легко застосовувати на практиці.
Зазвичай для тестування всі спостереження розбивають на дві групи. У всіх тестах
перевіряють гіпотезу про рівність дисперсій у цих групах:
22
01 2
:H
.
Якщо таку гіпотезу прийняти, то це означатиме, що гетероскедастичність не є
статистично значущою, тобто її наявність можна не враховувати.
Усі критерії визначення гетероскедастичності можна поділити на дві групи: загальні та
регресійні. Перший тип критеріїв справедливо вважають найпростішим у застосуванні,
проте, у разі визначення гетероскедастичності немає жодної інформації про подальшу
оцінку моделі
. Другий тип критеріїв дозволяє оцінювати вагові коефіцієнти для
зваженого методу найменших квадратів, проте, використання таких критеріїв не завжди
статистично коректне. Іншими словами, якщо регресійний критерій не виявляє
гетероскедастичності, то це не обов'язково означає, що гетероскедастичності немає.
Коректним буде висновок, що немає гетероскедастичності певного вигляду.
Серед різноманіття тестів на гетероскедастичність
до загальних належить критерій
Голдфелда – Квондта, а до регресійних – критерії Х. Глейзера та Х. Уайта.
4.3.1. Критерій Голфельда – Квондта.
Напевно, найбільш популярним формальним критерієм перевірки гетероскедастичності
є критерій, що його запропонували С. Голдфельд і Р. Квондт. Його використовують, коли
всі наявні спостереження можна поділити за деякою ознакою на дві групи. У випадку
однієї незалежної змінної спостереження з найменшими значеннями можуть становити
одну групу, а другу – спостереження з найбільшими значеннями незалежної змінної.
Також можна поділяти за значеннями залежної
змінної.
Нехай сукупність n спостережень розбита на дві групи розмірами
1
n і
2
n . Частину
спостережень із середніми значеннями можна вилучити. Емпіричні дослідження свідчать,
що для проведення тесту вилучають від 15 до 30 % спостережень із середини вибірки. У
цьому випадку
12
nn n. Щоб застосувати критерій Голдфельда – Квондта, слід оцінити
модель за МНК окремо на кожній підвибірці й знайти:

119
2
1
ˆ – оцінку дисперсії збурень за першою групою спостережень;
2
2
ˆ – оцінку дисперсії збурень за другою групою спостережень.
У припущенні, що гетероскедастичності немає, статистика
2
1
2
2
ˆ
ˆ
pr
F
має розподіл Фішера з
1
nk ,
2
nk степенями свободи.
Слід зауважити, що дисперсія першої групи обов'язково має бути більшою за дисперсію
другої групи. Якщо така властивість не виконується, то нумерацію груп змінюють на
протилежну.
Таким чином, якщо
22
12
ˆˆ
, то обчислюють статистику
2
1
2
2
ˆ
ˆ
pr
F і порівнюють її із
критичним значенням (теоретичним)
12
(
;;
)
teor
FFnknk
, знайденим за вибраним
рівнем значущості
у таблиці розподілу Фішера з
12
;nkn k
степенями свободи. Якщо
22
12
ˆˆ, то обчислюють статистику
2
1
2
2
ˆ
ˆ
pr
F і порівнюють її із критичним значенням
21
(
;;
)
teor
FFnknk, знайденим за вибраним рівнем значущості у таблиці розподілу
Фішера з
21
; nknk степенями свободи.
Якщо практичне значення
pr
F менше, ніж теоретичне, то вважають, що
гетероскедастичності немає. Якщо
pr teor
FF , то вважають, що гетероскедастичність
існує.
4.3.2. Критерій Уайта
Основним припущенням цього критерію є те, що якщо гетероскедастичність існує, то
це може бути пов'язане з тим, що дисперсія похибок деяким, можливо, досить складним
чином, залежить від регресорів, а тому гетроскедастичність має відобразитися в
залишках вихідної моделі. У 1980 році Х. Уайт запропонував метод тестування гіпотези
22
01 2
:H
без яких-небудь припущень про структуру гетероскедастичності.
У загальному вигляді тест Уайта можна представити у вигляді такого алгоритму:
1.
Спочатку оцінюють вихідну регресію за допомогою звичайного методу найменших
квадратів.
2.
Знаходять залишки моделі та оцінюють регресію квадратів залишків стосовно всіх
змінних із моделі, їхніх квадратів і попарних добутків. Наприклад, якщо початкова
модель має вигляд
0112233
,1,
ttttt
yxxxtn ,
то будують таку регресію:
2222
01122 33415263
712 813 923
ˆ
,1,.
ttttttt
tt tt t t t
vxxxxxx
xx xx x x t n
(4.4)
Визначають кількість регресорів у допоміжній моделі (у нашому випадку - 10).
Розраховують статистику
22
pr
nR ,
де
2
R – коефіцієнт детермінації моделі (4.4), яку слід порівняти з теоретичним значенням
статистики розподілу
2
teor
з
1n
степенями свободи та рівнем надійності
1
. Якщо
22
pr teor
, то гетероскедастичності немає.
Головною перевагою критерію Уайта є його універсальність і простота використання.
Крім цього, якщо критерій визначає наявність гетероскедастичності, то за його
допомогою можна оцінити вагові коефіцієнти для зваженого методу найменших
квадратів.
120
Водночас при відхиленні гіпотези
0
H цей тест не дає жодної вказівки на форму
гетероскедастичності.
4.3.3. Критерій Глейзера
Застосування цього критерію розглянемо на прикладі моделі
, 1,
ttt
y
xtn .
Спочатку оцінюємо модель за методом найменших квадратів і знаходимо залишки
ˆ
, 1,
t
tn. Потім будуємо регресію модуля залишків стосовно однієї з таких функцій:
ˆ
ttt
x
,
ˆ
ttt
x
,
1
ˆ
tt
t
x
,
ˆ
ln
ttt
x тощо.
При цьому використовуємо різноманітні функцій від незалежної змінної. Оцінюємо
кілька таких регресій. Далі обираємо ту регресію, яка має найбільший коефіцієнт
детермінації. Якщо ця регресія значуща, то гетероскедастичність наявна.
4.3.4. Критерій Бройша – Пагана
Цей тест застосовують у тих випадках, коли апріорно передбачено, що дисперсії
2
t
залежать від деяких додаткових змінних:
22
0
(), 1,
T
tt
f
tnz γ ,
де
12 ,
(
,,,
)
TT
ttt tp
zz zz – вектор незалежних змінних;
0
,
12
(
,,,
)
T
p
γ – невідомі
коефіцієнти.
Згідно із критерієм Бройша – Пагана оцінюють початкову регресію (4.1) і знаходять
вектор залишків
ˆ
, 1,
t
tn. Далі оцінюють допоміжну регресію
2
0
2
1
ˆ
ˆ
T
ttt
n
n
z γ .
Визначають суму квадратів залишків для допоміжної регресії
1
RSS та обчислюють
практичне значення статистики:
2
1
2
pr
RSS
.
Це значення порівнюють із теоретичним значенням розподілу
2
з p степенями
свободи та рівнем надійності
1:
22
(,1 )
teor
p
.
Якщо
22
pr teor
, то гетероскедастичність не виявляється.
4.4. Використання регресійних критеріїв для оцінювання моделей
За допомогою регресійних критеріїв можна оцінювати вагові коефіцієнти для
зваженого методу найменших квадратів.
За критерієм Уайта за умови адекватності допоміжної регресії (4.4) знаходять оцінки
квадратів залишків
2
ˆ
t
. Оцінки вагових коефіцієнтів
ˆ
t
w
для зваженого методу
найменших квадратів (модель (4.2)) обчислюють таким чином:
2
ˆ
ˆ
,1,.
tt
wtn
У разі виявлення гетероскедастичності за критерієм Глейзера для оцінювання вагових
коефіцієнтів використовують допоміжну регресію з побудованих із найбільшим
коефіцієнтом детермінації. Якщо, наприклад, такою моделлю виявилася залежність
ˆ
ttt
x
,
то оцінки вагових коефіцієнтів обраховують за формулою

121
ˆ
ˆ
ˆ
,1,
tt
wxtn .
За критерієм Бройша – Пагана вагові коефіцієнти обирають за допомогою формули
0
ˆ
ˆ
ˆ
T
tt
w z
γ
.
При цьому може спостерігатися ситуація, коли
0
ˆ
ˆ
0
T
t
z γ
. Якщо кількість таких
елементів відносно незначна, то їх просто не враховують, у протилежному випадку можна
спробувати використати мультиплікативну форму гетероскедастичності
0
2
, 1,
T
t
t
etn
z γ
.
Підсумовуючи, можна зазначити, що застосування зваженого методу найменших
квадратів загалом приводить до оцінок, що мають меншу дисперсію порівняно з
оцінками МНК, що, у свою чергу, поліпшує точність прогнозів і ефективність перевірки
статистичних гіпотез.
Приклад 4.1. Оцінювання моделі з гетероскедастичними збуреннями
Відомі доходи та витрати на споживання 30 сімей одного будинку.
C Y
190,
1
210,
5
200,
1
220,
6
221,
7
225,
3
227,
3
237,
7
208,
1
243,
4
215,
5
246,
2
230,
9
246,
7
211,
1
252,
8
230,
3
255,
3
259,
2
267,
0
250,
9
269,
0
234,
1
283,
3
271,
9
294,
8
285,
8
308,
9
380,
5
312,
0
267,
5
314,
3
322,
1
328,
0
375,
3
377,
7
297,
1
405,
8
372,
2
406,
0
287,
1
408,
2

122
C Y
390,
7
419,
5
490,
3
450,
9
504,
5
467,
7
338,
5
471,
3
496,
6
498,
5
461,
2
502,
8
521,
4
514,
8
482,
1
545,
3
452,
6
627,
6
1.
Побудувати регресію вигляду
01ttt
CYv
.
2.
Перевірити наявність гетероскедастичності збурень за критерієм Голдфелда –
Квондта.
3.
Перевірити наявність гетероскедастичності збурень за критерієм Глейзера.
4.
Перевірити наявність гетероскедастичності збурень за критерієм Уайта.
5.
У разі наявності гетероскедастичності оцінити модель за зваженим методом
найменших квадратів.
Розв'язання
1. Використовуючи звичайний МНК, знаходимо вигляд вибіркової регресійної
функції:
ˆ
23,3 0,85
tt
CY ,
2
0,81R .
2.
Побудуємо окремо дві регресії за першими
4
30 8
15
і останніми вісьмома
спостереженнями, попередньо відсортувавши всі спостереження за зростанням
незалежної змінної. Регресія за першими вісьмома спостереженнями має вигляд
ˆ
82,3 0,56
tt
CY ,
2
0,60R ,
2
ˆ11,87 . Регресія за останніми вісьмома
спостереженнями має вигляд
ˆ
449,5 0,04
tt
CY ,
2
0,04R ,
2
ˆ61,53 .
Знаходимо
1
2
ˆ
11,87
0,19
ˆ61,53
pr
F
. Оскільки 1
pr
F
, то дріб слід перевернути, таким
чином,
2
1
ˆ
61,53
5,18
ˆ11,87
pr
F
. Це значення більше за теоретичне (6;6;0,05) 4,28
teor
FF.
Робимо висновок, що гетероскедастичність існує.
3.
Для застосування критерію Глейзера треба знайти модуль вектора залишків:
ˆ
ˆ
23,3 0,85
tttt t
vCCC Y . Будуємо й оцінюємо допоміжні регресії:
ˆ
28,0 0,17
tt
vY
2
0,34R
ˆ
90,2 6,60
tt
vY
2
0,34R
1
ˆ
97,2 20853
t
t
v
Y
2
0,34R
2
ˆ
2,96 0,0002
tt
vY
2
0,32R
123
ˆ
330,53 62,35 ln
t
v
Y
2
0,34R
Найбільший коефіцієнт детермінації має остання модель. Вона адекватна, оскільки
практичне значення 13,67
pr
F
перевищує теоретичне (1;28;0, 05) 4,20
teor
FF
.
Таким чином, за критерієм Глейзера гетероскедастичність існує.
4.
Будуємо допоміжну модель квадрату залишків
2
2
2
ˆ
ˆ
23,3 0,85
ttt t t
vCC C Y
від
незалежної змінної та її квадрату:
22
ˆ
2485,8 9,75 0,008
ttt
vYY ,
2
0,344R .
Модель виявляється адекватною, оскільки практичне значення 7,07
pr
F перевищує
теоретичне (2;27;0, 05) 3,35
teor
FF. Таким чином, за критерієм Глейзера
гетероскедастичність існує.
5.
Оскільки виявлено гетероскдастичність, то модель треба оцінювати за зваженим
методом найменших квадратів. Для цього слід знайти оцінки вагових коефіцієнтів
t
w
. За
методом Глейзера їх знаходять за допомогою формули
ˆ
330,53 62,35 ln
tt
wY
, а за
критерієм Уайта
2
ˆ
2485,8 9,75 0,008
ttt
wYY .
Знаходимо нові змінні
*
t
t
t
C
C
w
,
*
t
t
t
Y
Y
w
.
Метод Глейзера Метод Уайта
W C* Y* W C* Y*
3,00 63,3
0
70,1
0
7,7
7
24,
45
27,
07
5,92 33,7
7
37,2
3
8,6
4
23,
16
25,
53
7,24 30,6
3
31,1
3
11,
75
18,
87
19,
18
10,5
7
21,4
9
22,4
8
17,
52
12,
97
13,
57
12,0
6
17,2
6
20,1
8
19,
65
10,
59
12,
39
12,7
7
16,8
7
19,2
7
20,
61
10,
46
11,
94
12,8
9
17,9
1
19,1
3
20,
77
11,
12
11,
88
14,4
2
14,6
4
17,5
3
22,
73
9,2
9
11,
12
15,0
3
15,3
2
16,9
8
23,
49
9,8
0
10,
87
17,8
3
14,5
4
14,9
8
26,
78
9,6
8
9,9
7
18,2
9
13,7
2
14,7
1
27,
31
9,1
9
9,8
5
21,5
3
10,8
8
13,1
6
30,
86
7,5
9
9,1
8
24,0
1
11,3
3
12,2
8
33,
47
8,1
2
8,8
1
26,9
1
10,6
2
11,4
8
36,
44
7,8
4
8,4
7
27,5
3
13,8
2
11,3
3
37,
08
10,
26
8,4
1
28,0
0
9,55
11,2
3
37,
55
7,1
2
8,3
7
30,6
6
10,5
1
10,7
0
40,
22
8,0
1
8,1
6
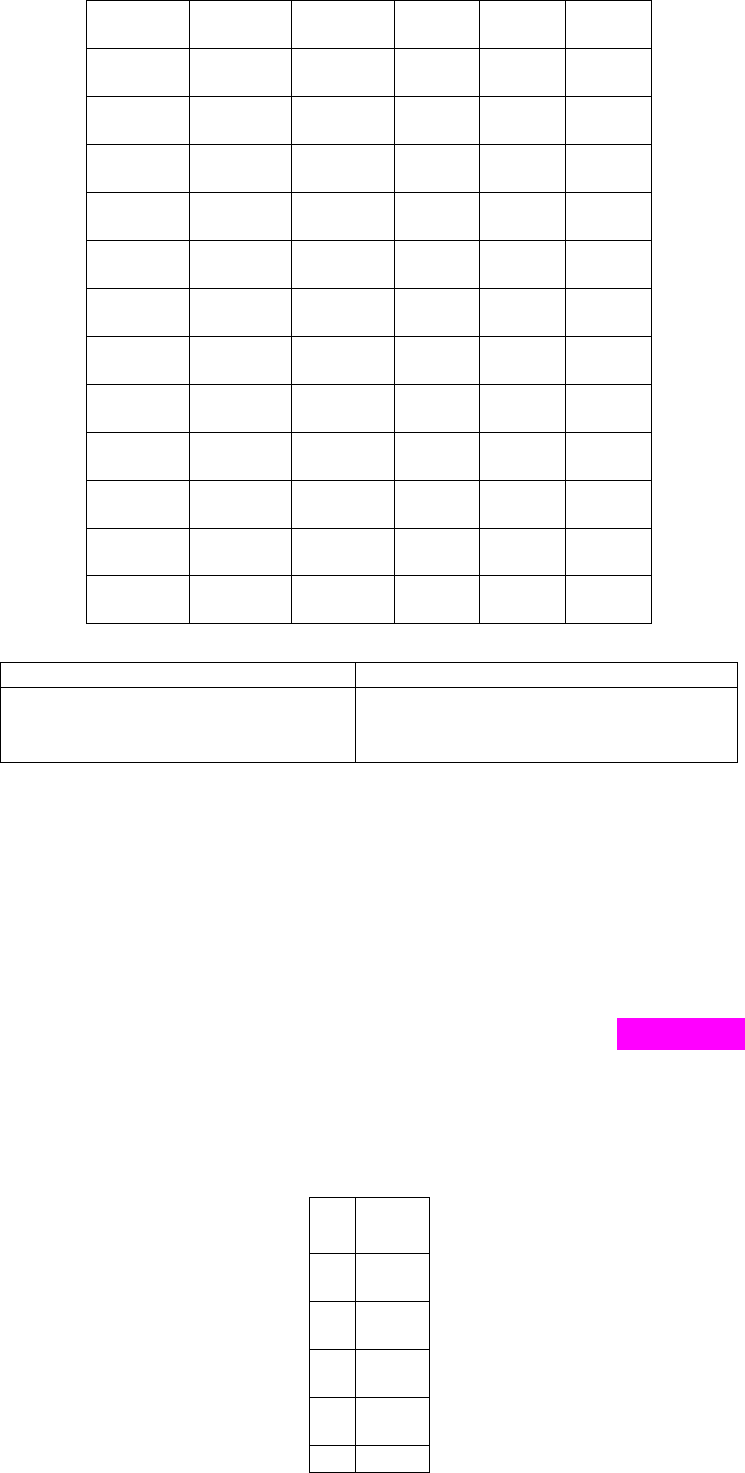
124
39,4
6
9,51
9,57
48,
96
7,6
7
7,7
1
43,9
3
6,76
9,24
53,
44
5,5
6
7,5
9
43,9
5
8,47
9,24
53,
47
6,9
6
7,5
9
44,2
9
6,48
9,22
53,
81
5,3
4
7,5
9
46,0
0
8,49
9,12
55,
54
7,0
4
7,5
5
50,5
0
9,71
8,93
60,
18
8,1
5
7,4
9
52,7
8
9,56
8,86
62,
56
8,0
6
7,4
8
53,2
5
6,36
8,85
63,
06
5,3
7
7,4
7
56,7
5
8,75
8,78
66,
82
7,4
3
7,4
6
57,3
0
8,05
8,78
67,
40
6,8
4
7,4
6
58,7
7
8,87
8,76
69,
02
7,5
5
7,4
6
62,3
5
7,73
8,75
73,
02
6,6
0
7,4
7
71,1
1
6,36
8,82
83,
33
5,4
3
7,5
3
Оцінюємо регресію
**
01ttt
CY
:
За методом Глейзера За методом Уайта
**
0,10 0,909
tt
CY ,
2
0,99R .
**
0,001 0,917
tt
CY ,
2
0,98R .
Як бачимо, остаточні оцінки, знайдені за зваженим методом найменших квадратів
значно відрізняються від оцінок звичайного МНК. Зокрема, побудовані регресії свідчать,
що сім'ї витрачають 91 % від доходів на споживання, тоді як оцінки звичайного МНК
показували лише 85 %.
Задачі
Група А
Задача 4.1. Доведіть, що для регресії
01ttt
yxv
, де D
t
vconst, дисперсія
оцінки
1
ˆ
, отримана за допомогою зваженого методу найменших квадратів, менша за
дисперсію МНК-оцінки.
Задача 4.2. Під час побудування регресії
011 22tttt
y
xxv
було отримано такий
вектор залишків:
t
ˆ
t
v
1
-
0,50
2
-
1,68
3
0,
41
4
1,
68
5
1,
125
t
ˆ
t
v
62
6
1,
93
7
-
2,04
8
-
0,39
9
1,
53
1
0
-
1,52
1
1
-
1,07
1
2
-
1,91
1
3
0,
95
1
4
-
3,46
1
5
2,
84
1
6
4,
38
1
7
-
4,59
1
8
2,
23
1
9
3,
82
2
0
-
1,76
2
1
2,
48
2
2
3,
57
2
3
4,
47
2
4
3,
44
Перевірте наявність гетероскедастичності залишків за критерієм Голдфелда – Квондта,
поділивши всі спостереження на дві групи по вісім елементів у кожній,
0,01
.
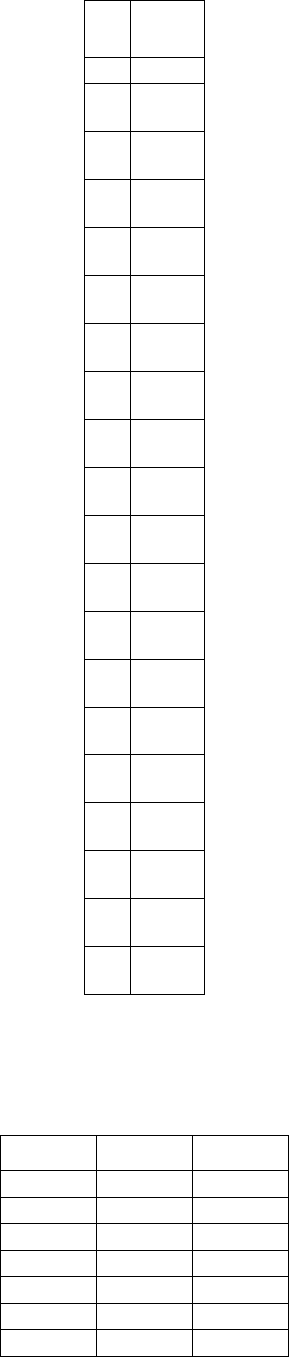
Задача 4.3. Відомі спостереження за величинами
12
,xx таy .
y
1
x
2
x
11 1 4
27 4 8
23 5 6
26 3 8
27 6 7
21 3 7
21 5 5
Оцініть регресію
011 22tttt
y
xxv
, якщо оцінка коваріаційної матриці має
вигляд

126
1, 3 0 0
00,8 0
000,9
.
Група Б
Задача 4.4. Відома така статистична інформація про змінні y та x :
y
x
7,11
9,73
13,3
2
16,5
3
14,0
4
19,2
8
10,9
7
20,1
5
17,0
8
23,7
4
15,7
8
23,8
7
19,0
9
25,5
5
17,2
3
25,8
0
16,4
1
27,8
9
23,7
0
28,8
1
15,4
4
29,2
9
19,9
4
30,4
6
24,2
5
31,4
0
19,3
8
31,6
3
24,5
7
32,2
9
23,9
7
34,0
2
24,8
3
34,0
3
10,2
8
34,3
2
22,9
7
36,7
0
32,3
1
36,9
7
29,5
0
39,0
5
38,0
7
39,2
6
20,6
5
39,8
5
23,7
6
40,5
0
27,6
4
42,3
1
1. Перевірте наявність гетероскедастичності залишків для моделі
01ttt
yxv за
критеріями (
0,01
):
