Черняк О.І. та ін. Економетрика

Подождите немного. Документ загружается.

127

 Голдфелда – Квондта;



Глейзера;



Уайта.

2. Якщо гетероскедастичність виявлено, то оцінити модель за зваженим методом

найменших квадратів, використовуючи оцінки вагових коефіцієнтів у формі



Глейзера;



Уайта.

Задача 4.5. Відома статистична інформація про змінні

та x :

8,96

,75

18,8

,58

19,0

,75

20,9

,23

23,1

,39

23,8

,54

24,7

,90

24,9

,14

26,1

,07

27,2

,03

27,5

,90

29,0

,70

29,3

,08

30,3

,38

30,3

,85

30,7

,48

30,8

,76

32,0

,49

33,4

,82

33,4

,07

34,3

,95

36,1

,18

36,2

,17

39,6

,69

41,3

128

1. Перевірте наявність гетероскедастичності залишків для моделі

01ttt

yxv   за

критеріями (

0,01 ):

 Голдфелда – Квондта;



Глейзера;



Уайта.

2. Якщо гетероскедастичність виявлено, то оцініть модель за зваженим методом

найменших квадратів, використовуючи оцінки вагових коефіцієнтів у формі:



Глейзера;

 Уайта.

Задача 4.6. На основі даних задачі 1.15:

1. Визначте наявність гетероскедастичності за критеріями (0,01



 ):



Голдфелда – Квондта;



Глейзера;

 Уайта.

2. Якщо гетероскедастичність існує, то оцініть модель за допомогою зваженого методу

найменших квадратів, використовуючи оцінки вагових коефіцієнтів у формі:



Глейзера;



Уайта.

Задача 4.7. На основі даних задачі 1.16:

1. Визначте наявність гетероскедастичності за критеріями (

0,05



 ):



Голдфелда – Квондта;

 Глейзера;



Уайта.

2. Якщо гетероскедастичність існує, то оцініть модель за допомогою зваженого методу

найменших квадратів, використовуючи оцінки вагових коефіцієнтів у формі:



Глейзера;



Уайта.

Задача 4.8. На основі даних задачі 1.18:

1. Визначте наявність гетероскедастичності за критеріями (

0,1







Голдфелда – Квондта;



Глейзера;



Уайта.

2. Якщо гетероскедастичність існує, то оцініть модель за допомогою зваженого методу

найменших квадратів, використовуючи оцінки вагових коефіцієнтів у формі:



Глейзера;

 Уайта.

Задача 4.9. На основі даних задачі 1.20:

1. Визначте наявність гетероскедастичності за критеріями (0,05



 ):



Голдфелда – Квондта;



Глейзера;

 Уайта.

2. Якщо гетероскедастичність наявна, то оцініть модель за допомогою зваженого

методу найменших квадратів, використовуючи оцінки вагових коефіцієнтів у формі:



Глейзера;



Уайта.

Задача 4.10. На основі даних задачі 2.15:

1. Визначте наявність гетероскедастичності за критеріями (0,05



 ):



Голдфелда – Квондта;



Глейзера;



Уайта.

129

2. Якщо гетероскедастичність наявна, то оцініть модель за допомогою зваженого

методу найменших квадратів, використовуючи оцінки вагових коефіцієнтів у формі:



Глейзера;

 Уайта.

Задача 4.11. На основі даних задачі 2.18:

1. Визначте наявність гетероскедастичності за критеріями (

0,1



 ):



Голдфелда – Квондта;

 Глейзера;



Уайта.

2. Якщо гетероскедастичність наявна, то оцініть модель за допомогою зваженого

методу найменших квадратів, використовуючи оцінки вагових коефіцієнтів у формі:



Глейзера;



Уайта.

130

Розділ 5. Модель лінійної регресій з автокорельованими збуреннями

5.1. Описання моделі

У цьому розділі ми розглянемо регресійні моделі, у яких порушено припущення 3 – про

незалежність збурень.

Є кілька ситуації, у яких збурення в моделях лінійної регресії можуть бути

корельованими.

Автокореляцiя, або часова кореляція збурень виникає в моделях, побудованих за

даними, які є часовими рядами. Такий тип кореляції збурень пов'язаний з тим, що деякі

економiчнi системи мають, так би мовити, інерцію, тобто якщо в деякий момент часу з

певних причин виникло відхилення від закономірної поведінки (нагадаємо, що збурення і

відтворюють в моделі

такі відхилення), то вплив цього може спостерігатись протягом

кількох наступних періодів часу. Нехай, наприклад, ми вивчаємо рівень безробіття за

допомогою деякої моделі. У певний момент часу фактичний рівень безробіття був

більшим, ніж розрахований з моделі. Оскільки для того, щоб зменшити рівень безробіття,

потрібен час, то логічно очікувати, що i наступний фактичний рівень

безробіття також

буде більшим, ніж теоретичний. Якщо згадати інтерпретацію збурень, то стане зрозуміло,

що останні міркування суперечать припущенню про некорельованість збурень. Цю

ситуацію ми розглянемо в підрозд. 5.1–5.7.

Однак наявність автокореляції залишків може свідчити (і це часто відбувається на

практиці) про неправильне визначення моделі. Ми розглянемо кілька найбільш

поширених причин такого

явища в підрозд. 5.8.

Спочатку домовимось про термінологію. Як і в попередньому розділі, літерою 

позначимо вектор збурень у вихідній моделі, а літеру  зарезервуємо для позначення

некорельованих і гомоскедастичних збурень.

Розглянемо модель лінійної регресії



yX υ



 , (5.1)

у якій вектор збурень   

(

)

має такі властивості:

1.  M0, 1,

tn.

2. Рівність дисперсій  

D= M const, 1,

tn.

3. Корельованість

cov( , ) 0,



 .

4. Некорельованість збурень та регресорів cov

(

)

, , ,

tsj

xts



 .

5. (Додаткове) збурення

 нормально розподілені для всіх t.

Припущення 2 і 3 зручно записувати в матричному вигляді:





D υ , (5.2)

де

0 – спільне значення дисперсії збурень;



– додатно визначена недіагональна

матриця, на головній діагоналі якої стоять одиниці, матриця



є кореляційною матрицею

збурень.

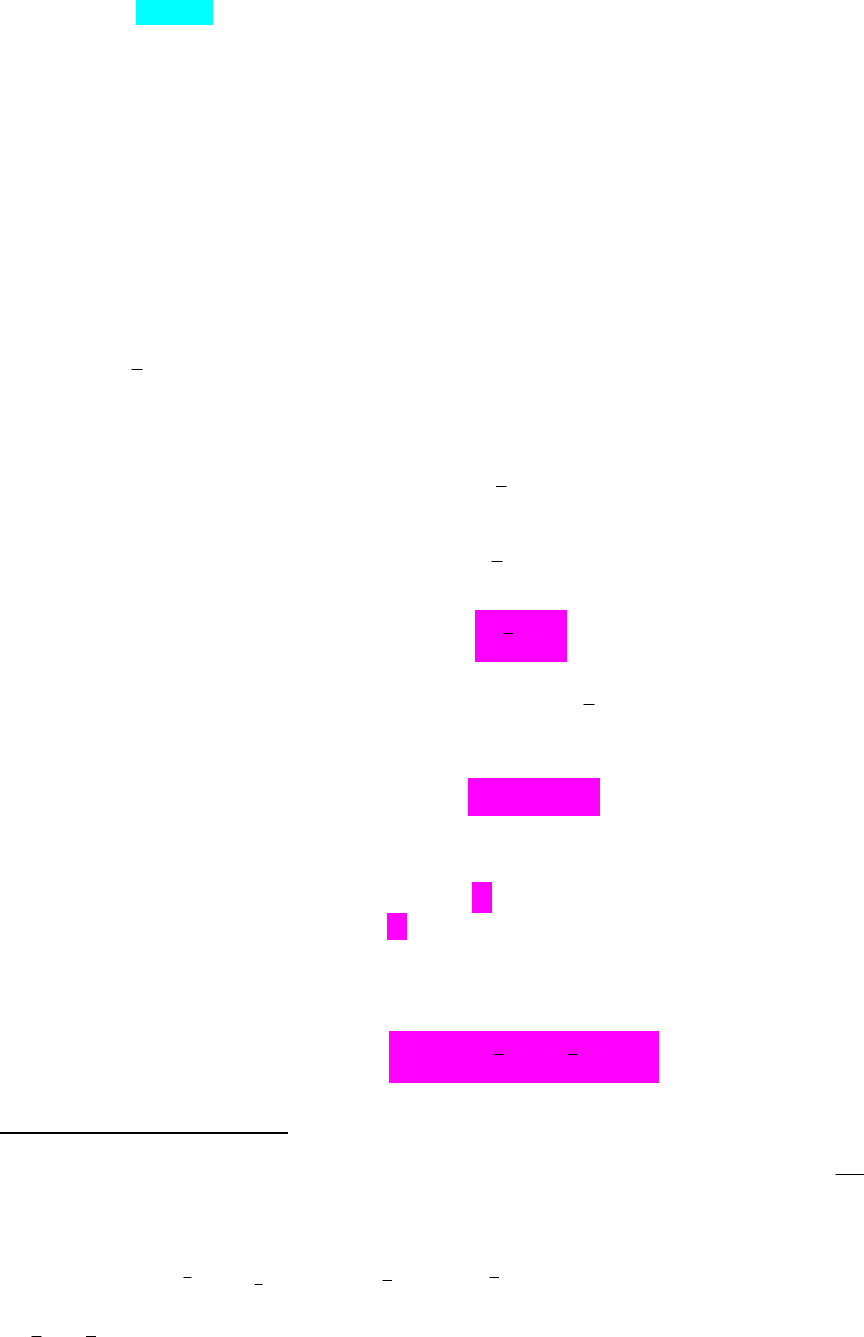
131

Зауваження. Останнім часом також вивчають моделі, побудовані за так званими

панельними даними, збурення в яких одночасно гетероскедастичні та корельовані. Такі

моделі буде розглянуто в розд. 11.

Наслідки впливу автокорельованостi збурень на оцінки методу найменших квадратів:

1. Оцінки МНК будуть незміщеними, але не будуть ефективними (не матимуть

найменшої дисперсії).

2.Стандартні оцінки коварiацiйної матриці оцінки МНК будуть зміщеними, i, як

наслідок, процедури перевірки гіпотез та iнтервального оцінювання, основані на

стандартних статистиках, будуть некоректними.

5.2. Узагальнений метод найменших квадратів у випадку відомої кореляційної

матриці

Припустимо, що матриця  відома. Оскільки вона додатно визначена, то для неї існує

матриця





Уведемо такі позначення:



yy ,













 .

Помножимо рівність (5.1) ліворуч на матрицю





. З урахуванням уведених позначень

маємо



yXβε



. (5.3)

Зазначимо, що вектори коефіцієнтів β у моделях (5.1) i (5.3) збігаються. Знайдемо

коварiацiйну матрицю збурень ε в моделі (5.3). Спочатку обчислимо математичне

сподівання:





MMυυ



  



Запишемо діагональний розклад матриці  = UU

-1

, де  = diag(

), in 1, – діагональна

матриця, на діагоналі якої стоять власні значення матриці , а матриця U складається з власних

векторів матриці , записаних поспіль. Оскільки  додатно визначена, то всі її власні значення

додатні. Тоді





= U





-1

, де 



= diag( 



). Нам потрібна така властивість цієї матриці:







I . Зауважимо, що останню властивість мають і деякі інші матриці, причому наведена

не є найзручнішою серед них.

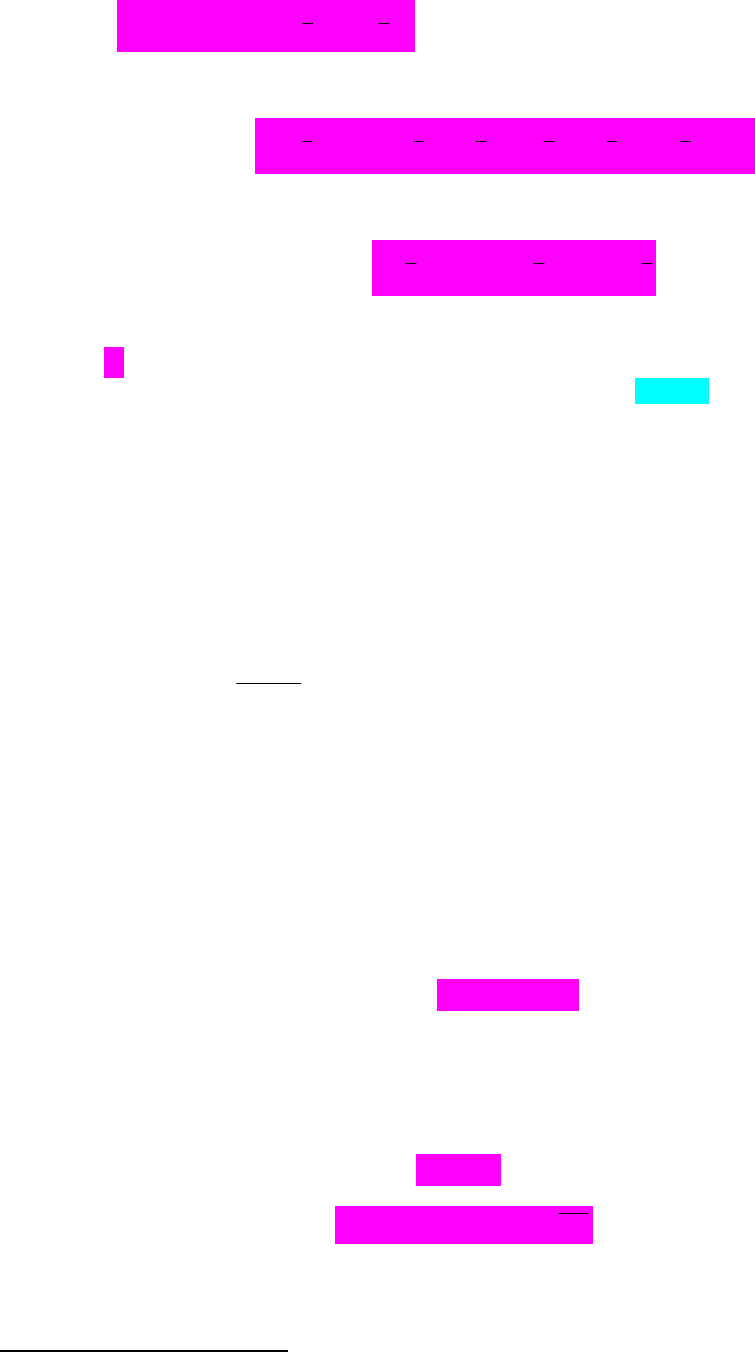
132

Отже,





DM Mεεε υυ (чому латинські букви D, M курсивом???)





 

111111

222222

(M ) Dυυ υ I     

. (5.4)

Ми скористались тим, що





111

TT TT

222

() ()υυ υ , а також тим, що лінійний

множник можна виносити за знак математичного сподівання. З (5.4) випливає, що

модель (5.3) є моделлю класичної лінійної регресiї. Отже, оцінки вектора параметрів

регресії β , знайдені в моделі (5.3) методом найменших квадратів, мають бажані

статистичні властивості, тобто задовольняють теоремі Гаусса – Маркова і, що є для нас

головним, цими оцінками можна користуватись для статистичних висновків.

Визначення. Оцінкою узагальненого МНК коефіцієнтів моделі (5.1) називається оцінка

звичайного МНК, знайдена за моделлю (5.3).

Зауваження.

Якщо матриця  діагональна, то узагальнений МНК точно збігається зі

зваженим МНК.

На практиці найчастіше матриця  невідома. Якщо не робити додаткових припущень

щодо структури матриці

, то її оцінити неможливо, оскільки за наявності n спостережень

ця матриця містить



невідомих параметрів. Отже, треба робити певні припущення

щодо збурень – розглядати моделі зі збуреннями спеціального вигляду. Найчастіше

розглядають моделі зі збуреннями, підпорядкованими процесу авторегресiї першого

порядку.

5.3. Узагальнений метод найменших квадратів у випадку AR(1)-збурень

Процесом авторегресії

першого порядку

((

))

AR називається послідовність випадкових

величин

, 0, 1, 2,

t

, яка задовольняє таке рівняння:





 

1ttt

, (5.5)

де

 – кількісний параметр, а

 мають ті самі властивості, що й збурення в класичній

лінійній регресії, тобто



M0

, (5.6)

 

Dconst, 1,

, (5.7)

cov( , ) 0,

sj   . (5.8)



Процеси авторегресії детально розглянуто в розд. 7. У цьому розділі, зокрема, міститься

виведення автокореляційної функції процесу

(

)

133

Нехай у моделі (5.1) збурення , 1,

tn підпорядковані процесу авторегресіїї першого

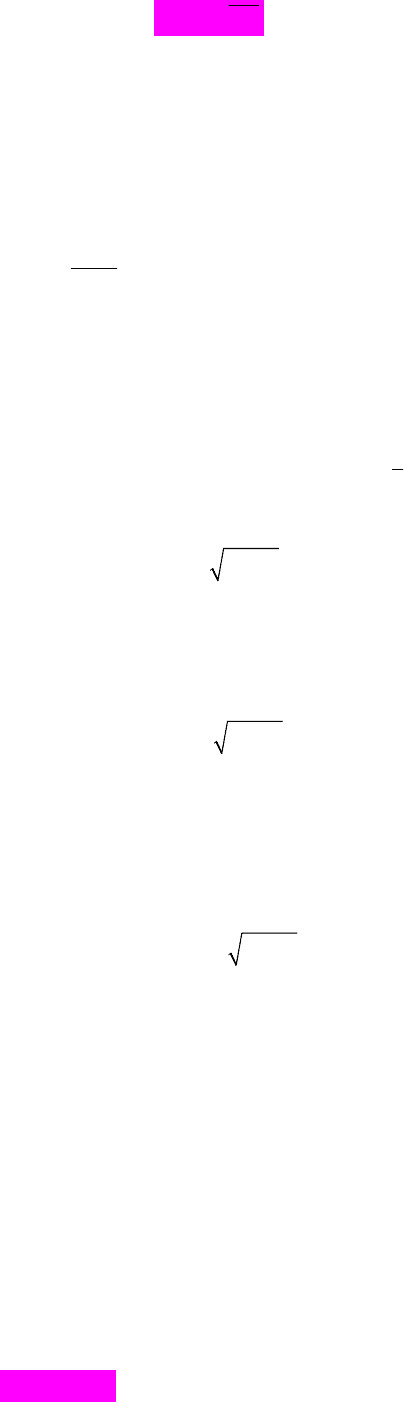
порядку, | | 1 . У розд. 7 показано, що коваріаційна матриця збурень набуває такого

вигляду:

123

nn n



 











 





















 (5.9)

Результати множення рівняння (5.1) на матрицю





у цьому випадку можна записати

в явному вигляді. Елементи вектора

дорівнюють

1yy, (5.10)

ii i

yy y in



 . (5.11)

Елементи j-го (0 1jk) стовпчика матриці

знаходять аналогічно:

xx , (5.12)

ij ij i j

xx x in



 . (5.13)

Якщо у вихідній моделі є постійний доданок, то перетворена модель не матиме

константи. Замість неї з'явиться змінна

, значення якої дорівнюють



 , (5.14)

1, 2

xin  . (5.15)

Перетворивши дані за формулами (5.10)–(5.15), можемо оцінювати модель (5.3)

методом найменших квадратів.

Зауважимо, що оцінка

 , коефіцієнта при змінній

x , є оцінкою постійного доданку у

вихідній моделі.

5.4. Критерій Дурбіна – Уотсона

Найчастіше для виявлення автокорельованості збурень користуються критерієм

Дурбіна – Уотсона. Нульовою гіпотезою при цьому є некорельованість збурень, а

альтернативою є те, що збурення підпорядковані процесу авторегресії першого порядку.

Позначимо через 

tn залишки методу найменших квадратів у моделі (5.1).

Значення статистики Дурбіна – Уотсона знаходимо за такою формулою:

134













ˆˆ

()

ttt

d . (5.16)

Можливі значення d належать інтервалу

(

0; 4

)

. Розподіл статистики Дурбіна – Уотсона

приблизно симетричний щодо двійки. Значення d, близькі до 2, указують на те, що немає

автокореляції. Значення, близькі до 0, указують на наявність автокореляції з додатним ,

значення, близькі до 4, указують на наявність автокореляції з від'ємним  . Параметрами

розподілу статистики Дурбіна – Уотсона є кількість спостережень і регресорів. Точний

розподіл статистики залежить від матриці незалежних змінних Х. У таблицях наведено

такі пари критичних значень, що для будь-якого вигляду матриці

Х точне критичне

значення лежить між табличними. Алгоритм застосування критерію Дурбіна – Уотсона є

таким:

Оцінюємо модель (5.1) за допомогою звичайного методу найменших квадратів.

За формулою (5.16) обчислюємо значення статистики Дурбіна – Уотсона.

Обираємо рівень значущості  і за таблицею критичних значень статистики

Дурбіна – Уотсона знаходимо верхнє й нижнє критичні значення d

і d

, а також

обчислюємо 4 – d

і 4 – d

. Зауважимо, що 0 < d

< d

< 2 < 4 – d

< 4 – d

< 4.

Робимо висновок за таким правилом:



Якщо d < d

, то є автокореляція з додатним .



Якщо d

< d < d

, то ми не можемо зробити жодного висновку, і цей інтервал

називається областю невизначеності.



Якщо d

< d< 4 – d

, то автокореляції немає.



Якщо 4 – d

< d < 4 – d

, то ми не можемо зробити висновку. Цей інтервал також

є областю невизначеності.



Якщо 4 – d

< d < 4, то наявна автокореляція з від'ємним .

Щодо областей невизначеності можна дати таку практичну рекомендацію: якщо

вибіркове значення d потрапляє до інтервалу невизначеності, то вважають, що існує

автокореляція.

5.5. Критерій Бройша – Годфрі

Критерій Дурбіна – Уотсона має кілька суттєвих недоліків. По-перше, його не можна

використовувати, якщо серед регресорів фігурують лагові значення залежної змінної.

Зокрема, при застосуванні будь-якого варіанта узагальненого методу найменших

квадратів у результаті перетворення даних у моделі завжди (явно чи неявно) з'являється



. Тому, користуючись критерієм Дурбіна – Уотсона, неможливо перевірити, чи зникла

автокореляція в моделі з перетвореними даними. По-друге, існують інтервали

невизначеності (між

d i

d ). По третє, строго кажучи, альтернативною гіпотезою є те,

що збурення генерує процес AR(1), що знижує потужність критерію за інших схем

утворення автокореляції.

Критерій множників Лагранжа (LM-критерій), що його розробили Т. Бройш і Л. Годфрі

[32], дозволяє подолати більшу частину з названих проблем. Його можна застосовувати й

за наявності лагових значень залежної

змінної. Альтернативою є те, що збурення генерує

процес ARMA порядку не вище за p. При 1p



критерій можна застосовувати замість

критерію Дурбіна – Уотсона.

135

Щоб перевірити гіпотезу про відсутність автокореляції до порядку p включно (якщо

ви пишете слово "включно", то треба написати від чого до чого, наприклад:

від а до р. У цьому разі можна обійтися без слова "включно"), треба спочатку

методом найменших квадратів оцінити вихідну модель





tt t

y x β , 1,tn (5.17)

і знайти залишки 

, 1,tn . Потім слід оцінити допоміжну регресію

 

     

11 2 2

ˆˆˆˆ

tt t t ptpt

x δ , 1,tn , (5.18)

у якій значення

s, яких немає, заповнити нулями. Нульову гіпотезу формалізуємо

таким чином:

01 2

:0,0,, 0

H     . (5.19)

Статистика критерію дорівнює

nR

, де

R – коефіцієнт детермінації в допоміжній

регресії (5.18). За нульової гіпотези вона має розподіл



з p степенями свободи. В умовах

малих вибірок для перевірки гіпотези (5.19) нерідко застосовують стандартний критерій

Фішера для перевірки сукупності лінійних обмежень.

5.6. Оцінювання у випадку невідомої кореляційної матриці збурень

Щоб застосувати підхід, описаний у підрозд. 5.3, нам не вистачає оцінки коефіцієнта

. Існує кілька способів знайти цю оцінку.

Вибірковий коефіцієнт кореляції залишків методу найменших квадратів. Його

знаходять як оцінку параметра регресії



стосовно





















ˆˆ

tttt

(5.20)

Оцінку Дурбіна – Уотсона обчислюють за такою формулою:



 ,

де d – вибіркове значення статистики Дурбіна – Уотсона.

Метод Кочрейна – Оркатта. Спочатку оцінюємо модель узагальненим методом

найменших квадратів, використовуючи оцінку



за формулою (5.20). Маючи нові

залишки, знаходимо для них вибірковий коефіцієнт автокореляції, який використовуємо

для знаходження нових оцінок. Процедура ітеративно повторюється, аж поки оцінки,

знайдені на двох послідовних етапах, не відрізнятимуться менше, ніж наперед заданий

рівень точності. У літературі зазначено, що асимптотично цей метод не має переваги

порівняно з двома попередніми.

Метод Хілдрета – Лу. Узагальнений метод найменших квадратів застосовують для

всіх

 з інтервалу від –1 до 1 із кроком 0,01. Обирають те значення, при якому сума

квадратів залишків мінімальна.

136

З розвитком програмного забезпечення найбільшої популярності набув метод, що

ґрунтується на нелінійній регресії й дозволяє одночасно знаходити оцінки



і β .

Запишемо основну модель (5.1) з

(

)

AR у звичайному вигляді:



     

01,12,2 1,1tttktkt

yxx x, (5.21)

де

1ttt

 . (5.22)

Підставимо (5.22) до (5.21):

01,12,2 1,1 1tttktktt

yxx x

 

       . (5.23)

Запишемо рівняння (5.21) для моменту



1 0 11,1 21,2 11,1 1tttktkt

yxx x



 

      . (5.24)

Помножимо обидві частини (5.24) на



і віднімемо від (5.23). Після перенесення



до

правої частини рівняння одержимо

0 1 1,1 1 1,1 1,1 1,1

(1 )

ttttktkktkt

yyxxxx



         . (5.25)

Збурення в моделі (5.25) задовольняють класичним властивостям

. Цю модель можна

розглядати як модель лінійної регресії

1 1 ,1 1 1,1 1 , 1 1 , 1tttt ktkktkt

yyxx x x



       ,

на параметри якої накладено такі обмеження:

, 1, 1

jk. Оскільки ці обмеження

нелінійні, то і регресія (5.25) нелінійна. Знаходження оцінок найменших квадратів у цій

моделі зведено до задачі нелінійної оптимізації. Той факт, що цей метод реалізовано в

більшій частині економетричного програмного забезпечення, дозволяє нам не вдаватись

то технічних деталей розв'язання проблем оптимізації.

Приклад 5.1. Оцінювання моделі з AR(1)-збуреннями

На базі даних про грошову масу М2 і ВВП України, наведених у таблиці нижче,

побудувати модель

ln ln

ttt

MYv



  ,

перевіривши залишки на наявність автокореляції.

(???)

Кварт

али

Грош

ова

маса М2,

млн грн

ВВП,

млн грн

1993/

47 53 3

,85



Унаслідок наявності лагового у серед регресорів оцінки будуть зміщеними, однак,

властивість спроможності зберігається.