Черепашков А.А., Носов Н.В. Компьютерные технологии, моделирование и автоматизированные системы в машиностроении

Подождите немного. Документ загружается.

Раздел 4. Компьютерная графика и геометрическое моделирование

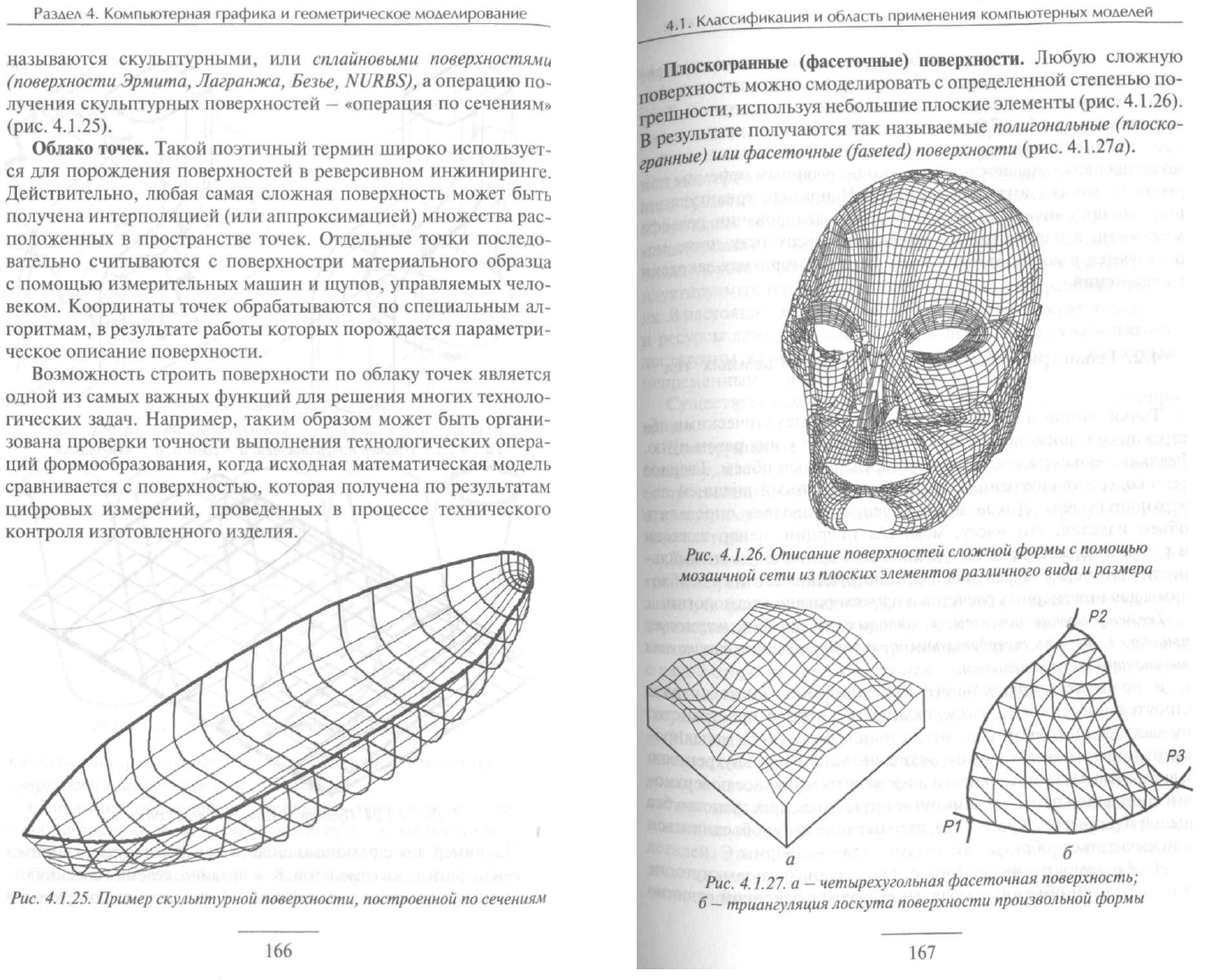
ЕСЛИ такие элементы, упрощенно моделирующие поверх-

ность, имеют форму треугольников (простейшая плоская фи-

гура), то такую поверхность называют триангуляционной. Три-

ангуляция (рис. 4.1.276), которая может рассматриваться как

простейший (и поэтому экономичный) способ поверхностного

моделирования, является достаточно популярным приемом при

решении многих инженерных задач. Например, триангуляция

широко применяется в геодезии для моделирования рельефа

местности, а плоскогранные кусочные поверхности часто ис-

пользуются в компьютерной графике и в алгоритмах закраски

изображений.

4.2. Геометрическое моделирование объемных тел

Точки, линии и поверхности являются математическими аб-

стракциями, поскольку хотя бы один размер у них равен нулю.

Реальные объекты всегда имеют определенный объем. Твердое

тело содержит внутренний объем, ограниченный внешней по-

верхностью тела. Такое представление позволяет определять

объем изделия, его массу, моменты инерции, центр тяжести

и т.п. Эти параметры зачастую являются критериями оптималь-

ности при оценке эффективности конструкции изделия и необхо-

димы для инженерных расчетов и проектирования технологии.

Геометрические объекты, у которых все размеры ненулевые,

принято называть твердотельными, а моделирование таких тел

называется твердотельным.

В процессе твердотельного моделирования также сначала

строятся поверхности, разделяющие трехмерное пространство

на части. Однако в отличие от чисто поверхностного моделиро-

вания при этом необходимо однозначно установить внутреннюю

и внешнюю части поверхности и проверить, чтобы все поверхно-

сти составляли при этом замкнутое внутреннее пространство без

щелей и разрывов. Кроме того, твердые тела могут объединяться

или вычитаться, образуя самые замысловатые формы.

Необходимость численного расчета и анализа замкнутости

и целостности объемных моделей выступает основной отличи-

168

4.2. Геометрическое моделирование объемных тел

169

тельной особенностью твердотельного компьютерного модели-

'ования по сравнению с поверхностным моделированием, вы-

зывает основные алгоритмические сложности при программной

реализации и требует значительных ресурсов памяти и быстро-

действия вычислительных машин. На ранних этапах развития

компьютерного геометрического моделирования это обстоятель-

ство существенно тормозило внедрение ЗD-моделей в САПР.

В прошлом веке сама возможность объемного твердотельного

моделирования была отличительным признаком небольшого

числа дорогих («тяжелых») автоматизированных систем, экс-

плуатируемых только на специализированных рабочих станци-

ях. В настоящее время возможности ЭВМ многократно возросли

и ресурсы даже не самых мощных персональных компьютеров

достаточны для твердотельного моделирования, которое стало

непременным атрибутом САПР всех уровней.

Существует несколько подходов твердотельного моделиро-

вания.

Конструктивная твердотельная геометрия (Constructive Solid

Geometry, или использование базовых элементов формы) опериру-

ет простейшими объемными примитивами, к которым относят

прямоугольную призму, треугольную призму, сферу, цилиндр,

конус и тор.

Для описания объемных примитивов используют рассмо-

тренные ранее аналитические поверхности (см. рис. 4.1.20). Если

замкнуть плоскостями открытые торцы, то аналитические по-

верхности легко разделят пространство на две части - свободную

внешнюю и замкнутую внутреннюю. Остается только указать,

с какой стороны поверхности находится объем тела. Например,

если замкнутая поверхность вырезает полость внутри другого

твердого тела, то объем будет находиться снаружи.

Над этими примитивами и полученными из них телами мож-

но выполнять математически хорошо отработанные булевы опе-

рации и автоматически получить линии их пересечения в ана-

литической форме. Конструктивная твердотельная геометрия

позволяет успешно моделировать большинство промышленных

Деталей. Этот подход гарантирует построение правильных твер-

дых тел и покрывает 60-70% потребностей моделирования, но

оставшаяся часть требует использования поверхностей.

Раздел 4, Компьютерная графика и геометрическое моделирование

170

4.2. Геометрическое моделирование объемных тел

динаты базовых точек всех элементов и топологическая инфор-

мация об их объединении.

представление оболочек и пространственных тел в виде кар-

касной сетки, состоящей из множества небольших ячеек, дав-

но и успешно используется в методе конечных элементов (рис.

4.2.1а) Однако в МКЭ, как правило, геометрическая модель

сначала экспортируется из СГМ, а только затем она делится на

элементы - генерируется сетка конечных элементов, координа-

ты узлов и топология которой необходимы для функциональ-

ного моделирования объектов и процессов. Если сетку сделать

достаточно густой и добавить информацию о заполнении ячеек

материалом, то такую геометрическую модель вполне можно

использовать для многих инженерных приложений, в которых

не требуется высокая точность описания формы поверхности

изделий.

Наиболее интересным и универсальным методом позицион-

ного представления объемных тел является «воксельная геоме-

трическая модель» (рис. 4.2.16). Весь объем, попадающий в габа-

риты моделируемого изделия, разбивается регулярной сеткой на

прямоугольные элементы и задается плотность заполнения каж-

дой ячейки материалом.

Воксельную модель можно считать трехмерным развитием

Растровых методов моделирования. Воксель (voxel) - термин, по-

денный для объема (от английского volume - объем) по аналогии

171

Представление с помощью границ (Bounded representation или

В-rep). Математически представляет собой наиболее общий под-

ход к описанию объемных тел и состоит в представлении тела

совокупностью ограничивающих его объем произвольных по-

верхностей. Границы объекта (вершины, ребра, грани, оболоч-

ки) хранятся в памяти компьютера в параметризованном виде

и должны точно стыковаться друг с другом. Однако чтобы в ито-

ге от произвольных поверхностей перейти к объему, уже значи-

тельно сложнее различать внешнюю и внутреннюю стороны всех

возможных их сочетаний, т.е. системы твердотельного модели-

рования должны хранить не только поверхности, ограничиваю-

щие твердое тело, но все связи между ними, контролировать зам-

кнутость и отсутствие щелей на стыках и швах. В В-rер-моделях

точность стыковки поверхностей составляет серьезную пробле-

му. Такие операции называют «сшивкой» поверхностей.

Несомненным достоинством этого подхода выступает то, что

представление тел с помощью границ позволяет моделировать

объекты произвольной формы и сложности.

Поверхности могут быть интегрированы в твердотельный мо-

деллер различными способами. Некоторые программы имеют

возможности автоматической сшивки поверхностей в твердое

тело. Но чтобы такая сшивка была осуществлена, необходимо,

чтобы поверхности с определенной точностью ограничивали

замкнутый объем. Выполнить такое условие часто бывает до-

статочно трудно, но оно является необходимым, чтобы продол-

жать процесс моделирования. В ряде случаев это не получается

автоматически и тогда приходится прибегать к «ручной», т.е.

диалоговой процедуре обнаружения проблемных участков и их

«ремонту» или наложению «заплат».

Другой подход - считать поверхности твердыми телами ма-

лой толщины. Проблема здесь в том, что при твердотельных опе-

рациях такие тела прорезают «щели» и целостность объема на-

рушается.

Позиционный подход к описанию объемных тел - это подход,

в соответствии с которым все рабочее пространство разбивает-

ся на элементарные объемы (ячейки) и деталь задают указанием

заполненных или пустых ячеек, т.е. геометрически описывается

простейший объемный элемент, например куб, задаются коор-

172

называемого: дерево конструирования — Feature manager, дерево

модели — Model Tree, навигатор модели — Model Navigator) (рис.

4.2.2).

Дерево построения можно считать графо-аналитическои мо-

лью процесса построения геометрической модели - наглядное

изображение алгоритма получения модели. В дереве построения

представлена вся последовательность составляющих моделируе-

мое тело объектов и операций с ними. Например, объекты могут

изображаться в «дереве» в виде иерархического списка, вклю-

чающего плоские эскизы и операции движения этих эскизов.

Дерево построения и графическая область экрана динамически

связаны. В режиме диалога пользователь может получить доступ

и модифицировать объекты, операции и образующие эскиз ли-

нии и контура.

В последние годы специалистами активно обсуждаются воз-

можности построения объемных геометрических моделей без

сохранения истории построения, за счет расширения возмож-

ностей вариационной параметризации [132]. Отказаться от

дерева построения позволяет использование так называемых

базовых конструктивных элементов (feature-based design), при-

менение достижений искусственного интеллекта и объектно-

ориентированного программирования.

Один из известнейших разработчиков программного обеспе-

чения для САПР — компания Siemens PLM Software [163] — в 2008 г.

анонсировала новую стратегию технического развития своих

программных продуктов, которую предложено называть ярким

и запоминающимся слоганом «Синхронное моделирование». Но-

вая методика моделирования синхронизирует геометрию и пра-

вила проектирования за счет применения механизма принятия

Решений, основанного на экспертной системе знаний.

Организационно изменения традиционной методики про-

ектирования заключаются в интерактивном порождении поль-

зователем ЗD-модели технического объекта из конструктивных

элементов, без обязательного предъявления ему дерева построе-

ния. Но при этом проектировщик должен получить достаточно

гибкий инструмент для редактирования геометрических форм.

Например, допускается динамическое перемещение конструкти-

вов, когда мышкой можно перетаскивать бобышку или отверстие

173

с пикселем (pixel) для плоскости. Варьируя плотность материала

в вокселях от нуля до заданного максимального значения по ана-

логии с цветом в растровом изображении, можно получать объ-

емные тела различной формы и структуры.

Воксельное представление позволяет описать объемное тело

с любой степенью погрешности в зависимости от числа использо-

ванных ячеек. Очевидно в пределе, когда число вокселей стремит-

ся к бесконечности, модель становится точной, но ее размерность

также бесконечно возрастает. Однако темпы роста вычислитель-

ных возможностей компьютерной техники позволяют считать

этот алгоритмически простой и интуитивно понятный метод гео-

метрического моделирования достаточно перспективным.

Все перечисленные подходы к моделированию тел использу-

ют не только описания тел и поверхностей, но и топологическую

информацию. Топология (topology) определяет структуру и связи

элементов модели. Например, представление тел с помощью

границ оперирует такие топологические понятия, как вершина,

ребро, грань и оболочка. Оболочки состоят из набора граней.

Оболочка отличается от поверхности тем, что кроме поверхно-

сти она несет информацию о связях с соседними гранями и об

ориентации по отношению к внутреннему объему тела.

С математической точки зрения одна внешняя и множество

из нескольких внутренних оболочек (возможно, и пустое) одно-

значно описывают твердое тело.

Но для редактирования объемного тела необходима еще ин-

формация о последовательности его построения.

Таким образом, компьютерная геометрическая модель твердо-

го тела, пригодная для использования в промышленных автомати-

зированных системах, должна включать:

— данные об объектах, составляющих тело;

— топологическую информацию о способах соединения объектов;

— информацию о последовательности построения модели.

4.2.1. Методы построений ЗD-молелей

•I

Управление геометрическими моделями. В универсальных

CAD-системах трехмерная модель формируется и управляет-

ся пользователем с использованием «дерева построения» (иначе

175

производительность визуального моделирования. Данная функ-

циональность важна и для задач анализа кинематики машин и ме-

ханизмов.

При отсутствии потребности в обязательном наличии дерева

построения становится возможным оперативное заимствование

конструктивов, созданных в других программах. Обычно при

перемещении модели из одной системы в другую дерево ее по-

строения теряется, что исключает полноценное редактирование

импортированной геометрии. Синхронная технология позво-

ляет включать в новый проект импортированные модели «как

свои собственные». На самом деле эффект непосредственного

включения достигается за счет использования интеллектуальных

методов распознавания конструктивных элементов и создания

в процессе трансляции точной копии «чужой» модели, но уже

в рамках своего геометрического ядра.

Существует и ряд ограничений данной методики. Основные

проблемы моделирования без сохранения истории построения,

при его реализации в универсальных САПР, проявляются в не-

достаточной масштабируемости моделей (время решения растет

значительно быстрее размера модели), ненатуральности (най-

денное решение не соответствует прагматическим ожиданиям

пользователя), отсутствия гарантии решения [132]. Например,

как указывают сами авторы синхронной методики, модель им-

портируется как одно тело, вследствие чего такие конструктив-

ные элементы, как отверстия, распознаются в виде полых цилин-

дров, а тонкостенные элементы рассматриваются как объекты

с независимыми поверхностями.

Идея проектирования, основанного на использовании стан-

дартных конструктивных элементов, не является новой [95, 147].

Но ее программная реализация достаточно сложна и требует объ-

единения достижений теории и практики многих направлений

развития компьютерных наук. Таким образом, синхронное гео-

метрическое моделирование можно классифицировать как но-

вую информационную технологию, основанную на комплексном

применении методов граничного представления объемных тел,

вариационной параметризации, искусственного интеллекта и

объектно-ориентированного программирования, предназначен-

ную для повышения уровня автоматизации ЗD-геометрического

4.2.2. Геометрические операции

Одними из самых популярных методов порождения объем-

ных примитивов являются операции движения плоских эскизов.

Плоский эскиз (Sketch) первоначально создается пользова-

телем на одной из базовых плоскостей системы координат (см.

рис. 4.1.12: ху —Top, xz — Front, yz — Right) вспомогательной пло-

скости, получаемой с помощью специальных команд, или пло-

ской грани объемной модели.

Обычно эскизы строятся в виде замкнутых линейных фигур,

ломаных линий или сплайнов. Если эскиз окажется разомкну-

тым, то твердотельный моделировщик автоматически превратит

его в плоский лист малой толщины (Thin). Кстати, на этом эф-

фекте основаны приемы моделирования объемных изделий из

листовых материалов (Shit metal), которые имеются практически

во всех машиностроительных САПР. Основными операциями

движения, которые применяются в прикладных программах гео-

метрического моделирования (подсистемах САПР), являются

следующие.

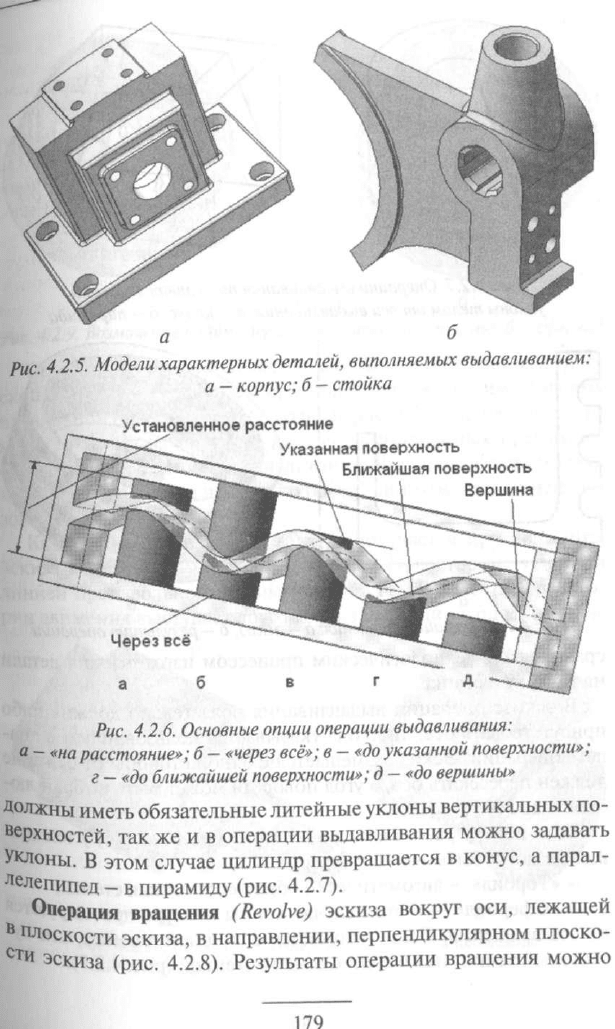
Операция выдавливания (Extrude) эскиза в направлении, пер-

пендикулярном плоскости эскиза. Это основная и наиболее ча-

сто используемая операция. На рис. 4.2.5 приведены примеры

моделей характерных деталей, выполненных преимущественно

с применением выдавливания.

Операции движения, как правило, снабжаются опциональ-

ными (дополнительными) параметрами. Например, показаны

различные результаты выдавливания эскиза в форме окружно-

сти, построенной на нижней плоскости коробки, по направле-

нию, совпадающему с положительным направлением оси z в за-

висимости от выбранной опции (рис. 4.2.6):

— выдавливание на определенное расстояние;

— выдавливание

«через всё»;

— выдавливание

до указанной поверхности;

— выдавливание

до ближайшей поверхности;

— выдавливание

до уровня указанной вершины.

Для образной иллюстрации применимости данной операций

удобно проводить аналогию с технологическим процессом литья

металлов или экструзии полимеров. Так же, как литые детали

178