Чефанов В.М. Основы гидравлики: Учебное пособие
Подождите немного. Документ загружается.


Основы гидравлики
Преобразуем эту систему уравнений, учитывая граничные условия. Так как
канал расположен горизонтально, то z
1
=z
2
. Течение будем рассматривать
турбулентным, поэтому
1
=
2
=1. Гидравлические потери на длине контрольного
объема l полагаем только местными, потерями на трение о стенки канала -
путевыми потерями давления – пренебрегаем, т.е.
2
2
1
u
pp
врврr
и местные
потери вычисляем по скорости в малой трубе, по скорости, с которой жидкость
втекает в контрольный объем. Боковые стенки контрольного объема между
сечениями 1 и 2 параллельны оси канала, трением жидкости о эти стенки
пренебрегаем, поэтому проекция боковой силы на направление оси, действующей со
стороны стенок на жидкость в контрольном объеме R=0. При таких допущениях и
граничных условиях система уравнений (а) – (в) приобретет вид:
2211
SuSu
22
2
2
2
1
21
2
1
uu
pp
u
p
врвр
)(
12221221
uuSuuuGSpp
.
Решая совместно эти уравнения, получим формулы для потерь при внезапном
расширении и для коэффициента местных потерь:
2
1
2
2
1
2
2
1
2
21
u
S
Suu
p
вр
, (5.7)
2
2
1
1
S
S
вр
. (5.7а)
Вопросы для самопроверки
1. Показать, как изменяются скорости и давления при внезапном расширении
потока при турбулентном течении; при ламинарном течении.
2. Провести преобразования для получения формул для потерь и коэффициента
потерь при внезапном расширении (формул(5.7) и(5.7а)).
В.М. Чефанов
111
Основы гидравлики
5.3. Истечение жидкости из отверстий и насадков при постоянном
напоре
Истечение из отверстий и насадков играет большую роль в различных
гидравлических и пневматических устройствах. Дроссельные шайбы, жиклеры,
форсунки являются примером использования насадков.
Основное уравнение гидравлики – уравнение Д.Бернулли было получено в
результате изучения истечения жидкости из отверстий.
Истечение может происходить в газообразную среду (свободное истечение)
или в жидкость (затопленное истечение) при постоянном или переменном напоре.
В зависимости от соотношения размеров отверстия и канала перед ним, а
также от расположения отверстия по отношению к стенкам различают отверстия с
полным, неполным, совершенным и несовершенным сжатием.
Истечение из отверстий и насадков характерно тем, что запас потенциальной
энергии, которым обладает жидкость в резервуаре, с превращается с бо́льшими или
меньшими потерями в кинетическую энергию истекающей струи или капель.
5.3.1 Отверстие в тонкой стенке
Насадок – это короткий трубопровод, непосредственно подсоединенный к
баку (сосуду) с жидкостью. Отверстием в тонкой стенке называют насадок, у
которого отношение длины к диаметру меньше 0,25. Рассмотрим истечение
жидкости из бака неограниченных размеров через отверстие в тонкой стенке
диаметром d (рис. 5.4). Условия задачи, кроме уже указанных, таковы: отверстие
достаточно удалено от свободной поверхности 1-1, дна и боковых стенок, так что
струйки жидкости подтекают к отверстию свободно и симметрично со всех сторон.
Истечение происходит в атмосферу с давлением p
а
при постоянном напоре или
перепаде давления p
0
+
gH. Отверстие будем считать малым d<<H. Требуется
определить скорость истечения и расход жидкости.
В.М. Чефанов
112
Основы гидравлики
u
2
а) б)
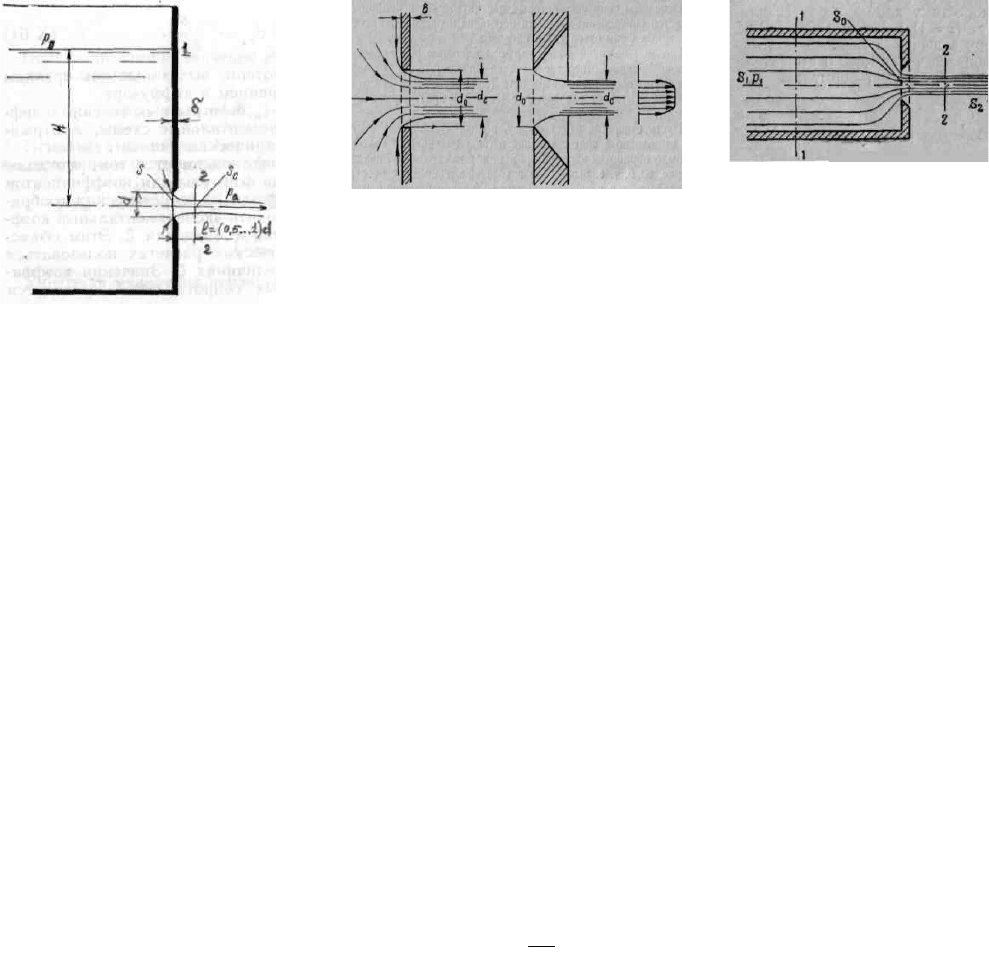
Рис 5.4 Истечение
жид-кости через
отверстие:
а) - в тонкой стенке; б) - с
ост-рой кромкой
u
Рис.5.5. Схема струйной
форсунки
Чтобы провести контрольную поверхность для решения поставленной задачи,
необходимо рассмотреть картину истечения жидкости.
Как показывают опыты, частицы жидкости, обтекая кромку отверстия,
движутся по криволинейным траекториям, что приводит к сжатию струи до
диаметра d
с
<d на расстоянии(0,5-1)d от стенки. В этом, сжатом, сечении давление в
струе становится равным давлению p
a
окружающей среды, так как линии тока в этом
сечении параллельны. Отношение площади сжатого сечения струи S
с
к площади
отверстия S называют коэффициентом совершенного сжатия струи
:
S
S
с
.
Сжатие потому называется совершенным, что стенки сосуда не оказывают
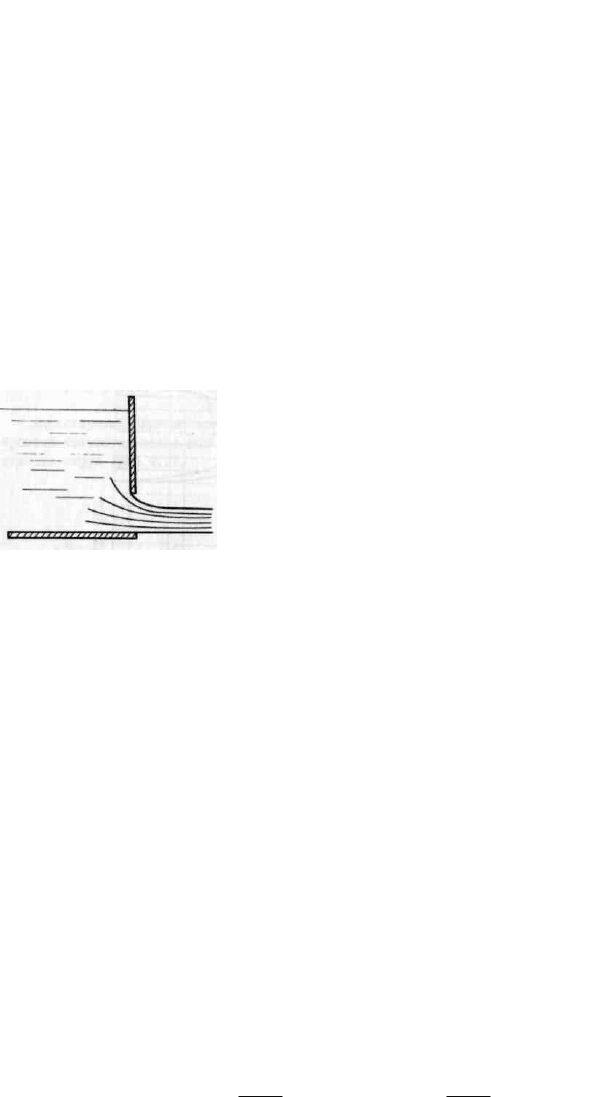
влияния на истечение. При несовершенном сжатии, которое происходит, например,
при истечении из струйной форсунки – цилиндрической трубки с круглым
отверстием в центре тонкостенного днища (рис. 5.5), струя сжимается меньше, чем
при совершенном сжатии за счет направляющего действия стенок трубки. Для
несовершенного сжатия коэффициент сжатия струи
н
можно рассчитывать по
эмпирической формуле /3/:
В.М. Чефанов
113
Основы гидравлики
2
37,0 n
н
,
где n=S/S
1
– отношение площади отверстия к площади сечения канала перед
отверстием;
- коэффициент совершенного сжатия струи, зависящий от числа
Рейнольдса.
При полном (всестороннем) сжатии происходит сжатие со всех сторон.
Если же с одной или нескольких сторон поток подтекающий к отверстию не
испытывает изменение направления, то сжатие истекающей струи будет
неполным (Рис.5.5,а).
Рис. 5.5,а Пример
непо-полного
сужения струи
После сжатого сечения жидкие частицы в струе
движутся вдоль оси струи, и одновременно с этим
движением под действием силы тяжести падают в
направлении ускорения свободного падения.
Рассмотренная картина истечения жидкости позволяет
определить место сечения в струе, в котором можно
говорить о скорости истечения. Несомненно, – это сжатое
сечение струи, в котором по сечению скорости жидкости постоянны. Поэтому
первая контрольная поверхность – сечение 1 – 1 струи совпадает со свободной
поверхностью в баке, а вторая располагается в сжатом сечении 2 – 2, где и нужно
определить скорость истечения жидкости.
Для выбранного контрольного объема записываем уравнения законов
сохранения:
2211
SuSu
- уравнение неразрывности (а);
r
p
u
pgz
u
pgz
22
2
2
2
22
2
1
111
- уравнение Бернулли (б).
Граничные условия для рассматриваемой задачи.
Сечение 1: z
1
=H; p
1
=p
0
; u
1
=0, так как размеры бака много больше диаметра
отверстия.
В.М. Чефанов
114
Основы гидравлики
Сечение 2: z
2
=0; p
2
=p
а
; u
2
=u=?; гидравлические потери являются местными
потерями, вычисляемыми по формуле Вейсбаха
2
2
u
p
r
.
Подставляя граничные условия в уравнение Бернулли и разрешая его
относительно искомой скорости истечения, получаем:
g
pp
Hgu
а
0
2
1
1
.
Обозначим величину
1
1
и назовем ее коэффициентом скорости. С его
использованием формула для скорости истечения принимает простой вид:
g
pp
Hgu
а
0
2
=
u
ид
.
В этой формуле u
ид
– скорость истечения идеальной (невязкой) жидкости,
равная
g
pp
Hgu
а
ид
0
2
.
Введение скорости истечения идеальной жидкости позволяет определить
коэффициент скорости как отношение скорости истечения вязкой жидкости к
скорости истечения жидкости невязкой:
ид
u
u
.
При таком определении коэффициента скорости очевидно, что его значение
будет определяться скоростью истечения идеальной жидкости и вязкостью реальной
жидкости. И действительно, значение скоростного коэффициента определяется
значением числа Рейнольдса:
du
ид
ид
Re
- с увеличением числа Рейнольдса
коэффициент скорости возрастает.
Расход определим в сжатом сечении струи:
g
pp
HgSQuSSuSuQ
а
идидидс
0
2
. (5.8)
В.М. Чефанов
115
Основы гидравлики
Здесь Q
ид
– объемный расход при идеальном истечении, когда жидкость идеальна
(гидравлические потери отсутствуют), а скорость распределена в сечении
равномерно и равна скорости истечения идеальной жидкости.
Величина
=Q/Q
ид
1 называется коэффициентом расхода,
показывающая, во сколько действительный расход отличается от расхода при
идеальном истечении, истечении без потерь и с однородным профилем скорости.
Поскольку скоростной коэффициент с увеличением числа Рейнольдса возрастает, а
коэффициент сжатия струи убывает (вязкость препятствует искривлению
траектории жидких частиц), то коэффициент расхода изменяется с увеличением
числа Рейнольдса неоднозначно; до Re
100 он возрастает, достигая значения
0,68, а затем асимптотически уменьшается к значению
0,61 при Re=10
5
.
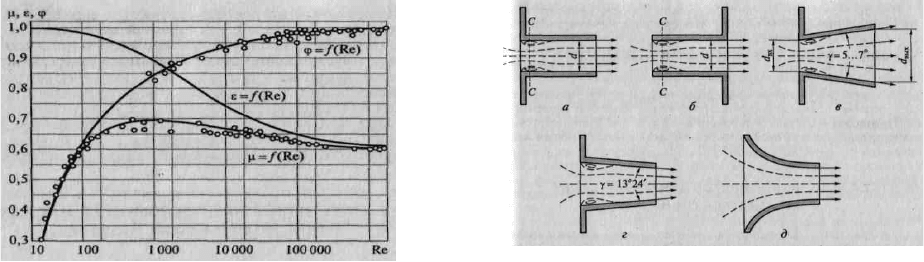
Рис. 5.6. Зависимость коэффициентов
скоро-сти, сжатия и расхода от числа
Рейнольдса для круглого отверстия в
тонкой стенке при полном совер-
шенном сжатии
Рис. 5.7 Различные виды насадков: а –
внешний цилиндрический насадок диа-
метром d; б - вну-тренний
цилиндрический насадок диаметром d; в –
конически расходящийся насадок; г -
конически сходящийся на-садок; д –
коноидальный насадок (сопло)
В области малых чисел Рейнольдса (Re<25) роль вязкости настолько велика,
что сжатие струи отсутствует (
1) и
.
Для маловязких жидкостей (вода, бензин, керосин и др.), истечение которых
происходит при больших числах Рейнольдса (Re10
5
), коэффициенты истечения
В.М. Чефанов
116

Основы гидравлики
практически не меняются. При полном и совершенном сжатии
0,64;
0,97;
0,62;
0,065 (рис.5.6).
5.3.2. Цилиндрический насадок
Внешний цилиндрический насадок представляет собой цилиндрическую
трубку или сверление в толстой стенке длиной l=(2 – 6) d без закругления входной
кромки. Отверстие в толстой стенке помимо цилиндрической формы может
конически расходящимся, конически сходящимся, коноидальным или их
комбинацией. Аналогично называют насадки, представленные на рис. 5.7.
Физическую картину истечения жидкости из цилиндрического насадка с
острой входной кромкой описывают следующим образом (рис. 5.8):
а) б)
Рис.5.8. Схема свободного истечения жидкости из
отверстия в толстой стенке цилиндрической формы
(цилиндрический насадок) диаметром d и длиной l
на безотрывном (а) и отрывном (б) режимах
Рис.5.9.Зависимость
коэффициен-та расхода от
числа Рейнольдса для
отверстия в тонкой стенке (1)
и цилиндрического насадка
(2)
обтекание острой кромки происходит с отрывом потока даже при низких числах
Рейнольдса (Re>5). При отрыве струя сужается, образуя узкое сечение на некотором
расстоянии от входной кромки. Между узким сечением и стенкой насадка
образуется отрывная область с вихревым течением. Если насадок имеет
В.М. Чефанов
117
Основы гидравлики
достаточную длину, отрывная область замыкается на стенки насадка и струя
заполняет все выходное сечение насадка. С увеличением числа Рейнольдса отрывная
область заметно увеличивается. В соответствии с конфигурацией струи жидкости
внутри насадка (канал с горловиной) давление на стенке по длине вихревой области
сначала резко уменьшается – до сжатого сечения, а затем начинает увеличиваться
(величина вакуума в отрывной зоне зависит от напора H и может быть определена
по формуле p
вак
=075
gH). Такая картина истечения жидкости из насадка определяет
все возможные режимы истечения:
1. неустойчивый, отрывной, с незамкнутой вихревой областью у
насадков с l/d<1,5;
2. устойчивый, безкавитационный, у насадков с l/d>1,5;
3. кавитационный, когда давление в вихревой области понижается до
давления равного или близкого давлению насыщенного пара жидкости (для воды с
температурой 0 -50
C при напоре H превышающем 12 –13 м).
Каждый и этих режимов имеет свои особенности. При коротких насадках
неустойчивый режим работы наблюдался в широком диапазоне чисел Рейнольдса
10
3
–10
5
и определяется рядом случайных причин. Такие короткие насадки не
рекомендуется для применения в гидросистемах из-за большого разброса значений
коэффициента расхода.
Насадки длиной l/d>1,5 обладают стабилизированным режимом истечения.
Вихревая область полностью замыкается на стенке насадка, жидкость полностью
замыкает выходное сечение. Коэффициент расхода насадка при бескавитационном
течении является функцией его относительной длины и числа Рейнольдса. С
увеличением относительной длины коэффициент расхода уменьшается из-за
увеличения потерь на трение, а при увеличении числа Рейнольдса – увеличивается;
его значение при Re>510
3
=0,82.
Кавитационный режим работы цилиндрического насадка наблюдается тогда,
когда минимальное давление в вихревой зоне станет равным или близким давлению
В.М. Чефанов
118
Основы гидравлики
насыщенных паров. Кавитация начинается вблизи сжатого сечения у стенок канала
образованием паровой или газовой каверны. Поток жидкости после каверны
движется в виде свободной струи, окруженной смесью пара и жидкости. По мере
увеличения скорости истечения происходит расширение кавитационной зоны.
С момента возникновения кавитации в цилиндрическом насадке его
коэффициент расхода, в отличие от истечения из отверстия в тонкой стенке,
уменьшается с развитием кавитационной каверны, приближаясь к значению
коэффициента расхода для отверстия в тонкой стенке.
Во избежание кавитации в цилиндрическом насадке входную острую кромку
устраняют заменой коническим участком, сходящимся с углом 20 (либо
скругленным) с относительной длиной l/d>1,5. Длина цилиндрической части может
быть любой, в зависимости от конструктивных требований, предъявляемых к
насадку. В частности, эта длина может быть равна нулю, при этом насадок
превращается в сужающийся конический.
Истечение через насадок рассчитывается с помощью уравнения Бернулли для
сечений O-O на свободной поверхности жидкости в баке и 2-2 на выходе из насадка.
Получим ту же формулу истечения, как и для отверстия в тонкой стенке. Но
величина коэффициента скорости в этом случае отличается от величины
коэффициента скорости для отверстия в тонкой стенке, так как кроме потерь на
обтекание кромок (внезапного сужения) будут еще и потери при расширении струи
после сжатого сечения С-С. Полагают, что общее сопротивление внешнего
цилиндрического насадка аналогично сопротивлению при входе в трубу из
резервуара ς=0,5 и коэффициент скорости φ≈0,82 /13/. Опытные данные близки к
этому значению при длине насадка (3…4) d. Коэффициент расхода цилиндрического
насадка ввиду отсутствия сжатия струм на выходе из него получается значительно
больше, чем при истечении из отверстия, т.е. µ=εφ=1φ=0,82. Таким образом, расход
через насадок примерно на 30% больше, чем через отверстие. хотя скорость
истечения примерно на 15% меньше, чем через отверстие.
В.М. Чефанов
119

Основы гидравлики
Вакуум в сжатом сечении струи в насадке получается тем больше, чем больше
скорость жидкости в сжатом сечении, т.е. чем больше напор перед входом в
насадок. Записывая уравнение Бернулли для сжатого сечения с-с и сечения на
выходе из насадка 2-2
ra
c
c
p
u
p
u
p
22
2
2
2
,
и полагая, что сжатие струи примерно такое же, как при истечении из отверстия в
тонкой стенке, т.е. коэффициент сжатия струи ε≈0,64, а S
c
=εS, получим
2
2
2
2
2
2
2
2
2
22
u
S
S
u
u
c
.
Потери давления между сжатым сечением и выходным определим как потери
на внезапное расширение по формуле Борда-Карно
2
2
2
2
2
1
1
22
u
uu
p
c
r
.
Полагая, что давление на свободную поверхность жидкости в резервуаре
равно атмосферному, т.е. p
0
=p
a
, из формулы для скорости истечения будем иметь:
gH
u
2
2
2
2
.
Подставляя полученные выражения для динамического давления и потерь в
уравнение Бернулли, получим для вакуума в сжатом сечении:
gHgHppp
caвак
75,01
1
1
1
2
2
2
.
Предельный напор перед насадком:
g
p
H
вакпр
пр
75,0
. Теоретически предельный вакуум
считают соответствующим давлению парообразования, давлению на-сыщенных
паров жидкости p
s
. Для воды при температуре 20°C величина
.24,0 м
g
p
s
С учетом
этого H
пр
=13,5 м. В инженерной практике такой вакуум не допускается. так как в
воде растворены различные газы. которые начинают выделяться при меньшем
В.М. Чефанов
120
