Buschow K.H.J. (Ed.) Concise Encyclopedia of Magnetic and Superconducting Materials

Подождите немного. Документ загружается.

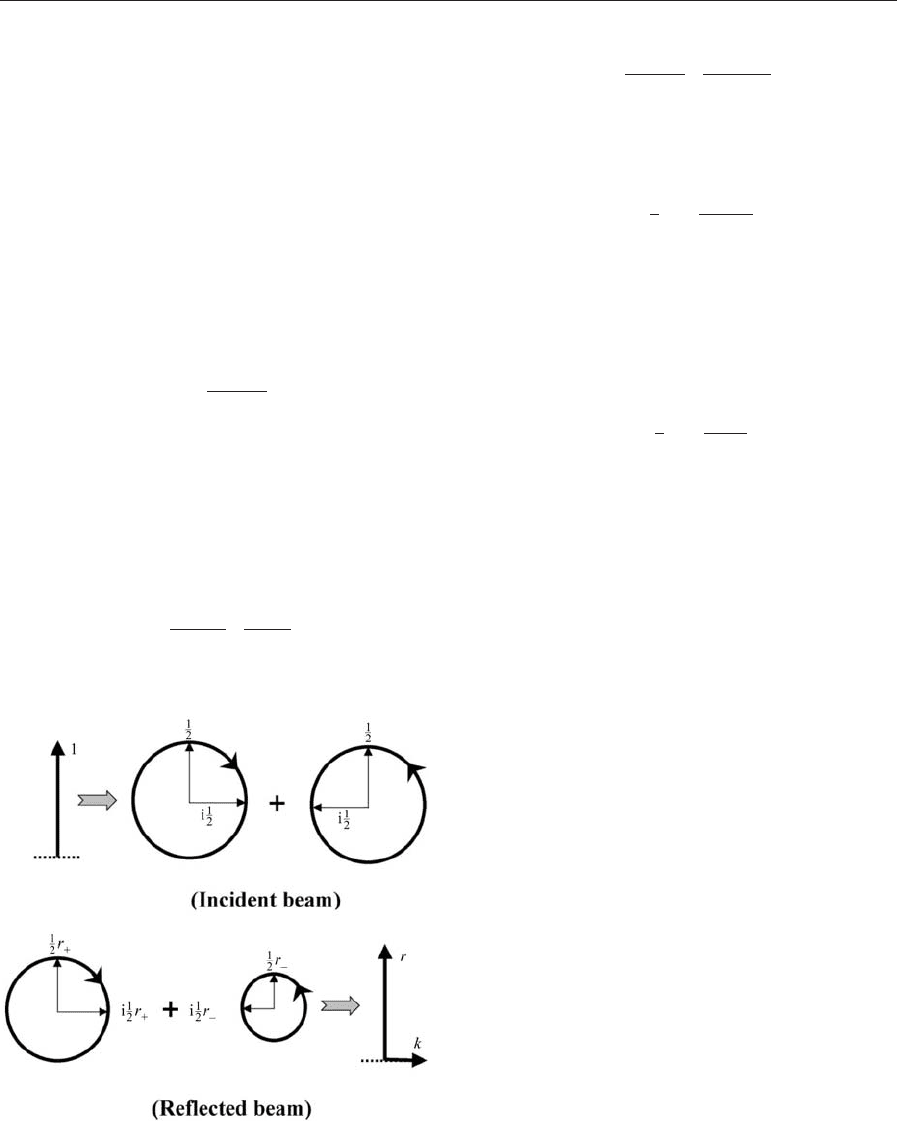
differential propagation properties of circularly po-

larized beams or optical modes (Gerber et al. 1992). It

transpires that a linearly polarized beam may be de-

composed into two counter-rotating circularly polar-

ized beams whose E vectors are equal and rotate in

opposite directions (i.e., clockwise ( þ) and anti-

clockwise ()). At normal incidence, these two beams

may be considered to propagate separately through

the medium with associated refractive indices n

and



given by

¼ nð17Q=2Þð10Þ

At a plane boundary between an incident medium

of refractive index n

and a semi-inﬁnite medium of

refractive index n

, the amplitude reﬂection coefﬁ-

cient is simply given by

 n

þ n

ð11Þ

Consequently, after reﬂection (or transmission),

the amplitudes of these two circular polarized modes

are different and when recombined result in the am-

plitude coefﬁcients r and k (or t and f ), as discussed

above. Figure 6 is a vector phase diagram that illus-

trates this. It is clear that after reﬂection and since

7Q751 these two modes result in amplitude reﬂection

and Kerr coefﬁcients given by

r ¼

þ r



 n

þ n

ð12Þ

and

k ¼

ðr

 rÞ

in

ðn

þ nÞ

ð13Þ

In most cases k5r, in which case it follows that the

complex Kerr rotation, as previously deﬁned in Eqn.

(5), is given by the following expression:

E 

inn

 n

ð14Þ

By ignoring boundary effects, a simpliﬁed calcula-

tion can also be carried out for the Faraday effect in a

slab of material of thickness d. In this case the two

circular modes suffer differential absorption owing to

the differing complex indices n

and n



. A straight-

forward calculation shows that a simple expression

for the complex Faraday rotation is

E 

pnQd

ð15Þ

where l

is the free-space wavelength of the radiation.

5. Summary

Magnetooptical effects, ﬁrst discovered by Michael

Faraday and John Kerr, can clearly be understood

phenomenologically, both in reﬂection and transmis-

sion, in terms of the existence of small electric ﬁeld

amplitudes that appear in the reﬂected and transmit-

ted ﬁelds in addition to the usual Fresnel amplitudes.

In longitudinal and polar orientations of the mag-

netization, with respect to the plane of incidence,

these extra magnetooptical components give rise to

elliptically polarized light. In the transverse orienta-

tion the magnetooptic component results in an in-

tensity change in the reﬂectivity of P-polarized light.

The intrinsic properties of the material, said to be

gyroelectric, are fully described by a skew-symmetric

permittivity tensor. Formal calculations can be car-

ried out for single surfaces and thin ﬁlms as well as

for multilayered systems. A full discussion of the

theoretical techniques used to deal with multilayer

systems and their properties is given in Magneto-

optical Effects, Enhancement of and Multilayer

Optical Film Modelling.

See also: Magneto-optics: Inter- and Intraband

Transitions, Microscopic Models of; Magneto-optic

Multilayers

Bibliography

Atkinson R, Lissberger P H 1992 Sign conventions in mag-

netooptical calculations and measurements. Appl. Opt. 31,

6076–81

Figure 6

Circular polarized modes leading to the normal

incidence polar Kerr effect.

170

Faraday and Kerr Rotation: Phenomenological Theory

Faraday M 1845 Experimental researches in electricity. Proc. R.

Soc. 5, 567–9

Freiser M J 1968 A survey of magneto-optic effects. IEEE

Trans. Magn. MAG-4, 152–61

Gerber R, Wright C D, Asti G 1992 Applied Magnetism.

Kluwer, London

Kerr J 1877 On rotation of the plane of polarisation by reﬂec-

tion from the pole of a magnet. Philos. Mag. 3, 321–43

Thomas J M (1991) Michael Faraday and the Royal Institution.

Adam Hilger, Bristol, UK

Verdet E 1854 Sur les proprie

s optiques de

veloppe

es dans les

Corps Transparents par l’Action du Magne

tisme. Ann. Chim.

Phys. 41, 370–412

R. Atkinson

The Queen’s University, Belfast, UK

Ferrite Ceramics at Microwave

Frequencies

The term ferrite is used to designate ferrimagnetic

materials. Ferrites are similar to magnetic alloys in

that both possess magnetic domains and exhibit

characteristic phenomena of saturation and hystere-

sis. However, ferrites are generally ceramics that are

hard, brittle, and are poor electrical conductors.

Typical values for the physical constants of ferrite

ceramics are:

Coefﬁcient of linear expansion ¼10

5

1

Specific heat ¼0.2 cal g

1

Thermal conductivity ¼0.015 cal s

1

Density ¼5gcm

3

The chemical formula for ferrites can vary signif-

icantly, and they can have cubic or hexagonal crystal

structure. Ferrites with spinel structure have the for-

mula MFe

, where the iron is trivalent and the

symbol M denotes a divalent metal from the series

þ2

,Mn

þ2

,Fe

þ2

,Co

þ2

,Ni

þ2

,Cu

þ2

,Zn

þ2

,or

þ2

. Another important family of ferrite com-

pounds are those with the garnet structure with

chemical formula M

, where M is a trivalent

metal from the lanthanide period of elements, such as

yttrium. Ferrites having hexagonal structure corre-

spond to the formula MFe

, where M is Ba or Sr,

M being divalent and Fe trivalent.

Ferrite ceramics are widely used in microwave

devices to control transmission path, frequency, am-

plitude, and phase of microwave signals. Accurate

dielectric and magnetic property measurements at the

operational frequency and temperature ranges are

needed for optimized development of these devices,

as well as to assist in the manufacture of the ferrite

itself. Both dielectric and magnetic losses must be

determined.

1. Microwave Measurements

A ferrite is characterized electrically and magnetically

by its complex permittivity:

e* ¼e

je

) ¼e

(1jtand

) and its complex per-

meability:

m* ¼m

jm

) ¼m

(1tand

), where tand

tand

denote dielectric and magnetic loss tangents,

and the free space permittivity e

and permeability

are given by 8.854 10

12

1

and 4p 

7

1

. The superscript * denotes that the

quantity is complex. The complex permittivity and

permeability are both temperature- and frequency-

dependent.

Dielectric losses for most ceramic ferrites are very

small (p5 10

4

) and usually vary linearly with fre-

quency. Magnetic losses depend on saturation mag-

netization, chemical composition, porosity and grain

size, and any applied static magnetic ﬁeld strength.

Magnetic losses vary nonlinearly with frequency, of-

ten by seven orders of magnitude over the frequency

range from 1 MHz to 25 GHz.

When an applied magnetic ﬁeld bias is applied in

the z-direction, the complex permeability becomes

anisotropic and is then generally written in diago-

nalized tensor form:

m; ¼ m

0 m

00m

ð1Þ

For the dielectric case, m

¼m

¼1 and all mag-

netic losses are 0. For a demagnetized ferrite,

¼m

, and magnetic permeability be-

comes a scalar quantity. For a partially magnetized

ferrite, m

¼m

and m

a1, tand

z,m

a0, where

tand

z,m

denotes the magnetic loss tangent parallel to

the applied tuning magnetic bias ﬁeld and m

the magnetic permeability transverse to the bias ﬁeld.

In a saturated ferrite, m

¼m

, and m

¼1,

tand

z,m

¼0.

The magnetization frequency of a ferrite is deﬁned

by f

¼g

, where g

is the gyromagnetic ratio

(35.19 MHz m/kA) and M

is the saturation mag-

netization (kA/m). At frequencies f less than f

, fer-

rites have high magnetic loss and are commonly used

as ferrite tiles in anechoic chambers or in other

shielding applications. Waveguide transmission line

techniques can be used for accurate magnetic char-

acterization for fof

(Baker-Jarvis et al. 1993).

Wireless communication system applications

employing ferrites (circulators and phase shifters)

usually operate at frequencies greater than the mag-

netization frequency. Magnetic losses rapidly de-

crease above f

, and transmission line techniques

cannot be used for accurate loss characterization.

The most accurate methods for measuring ferrite

171

Ferrite Cer amics at Microwave Frequencies

magnetic properties at microwave frequencies are

techniques that use resonant cavities or that incorpo-

rate the ferrite specimen as part of a dielectric reso-

nator system (LeGraw and Spencer 1956, Bussey and

Steinert 1958, Green and Kohane 1964, Green and

Sandy 1974, Ogasawara et al. 1976, Muller-Gronau

and Wolf 1983, Le Roux et al. 1988, Krupka 1991,

Krupka and Geyer 1996). Dielectric resonator system

techniques have greater sensitivity than cavity meth-

ods to magnetic loss for comparably-sized samples.

One measurement procedure, illustrated in Fig. 1 for

accurate evaluation of e

and m

and at frequencies

greater than f

, is to place a cylindrical sample in a

parallel plate waveguide (Courtney 1970) and:

Apply a large static magnetic ﬁeld (beyond ferro-

magnetic resonance) along the cylindrical z-axis to

saturate the ferrite specimen, causing m

¼1 and

tand

z,m

¼0. The ferrite specimen is equivalent to a

dielectric resonator, and e

and tand

may be meas-

ured with the TE

011

mode resonant frequency f and

system unloaded Q-factor Q

Demagnetize the specimen and measure the TE

011

mode resonant frequency f

and unloaded Q-factor

. The real permittivity and dielectric loss tangent

are known from the ﬁrst step, and the real magnetic

permeability m

and magnetic loss tangent tand

are

evaluated from the second.

Another measurement technique is to employ low-

loss dielectric sleeves operated with TE

011

mode

structure (Fig. 2). This system (Krupka and Geyer

1996, Geyer 1999) permits broadband permeability

characterization of a single ferrite sample at fre-

quencies near and far from the magnetization fre-

quency. The measurement bandwidth is realized by

the use of commercially available high-Q ceramic or

oriented single-crystal quartz resonators. The aspect

ratios and permittivities of the sleeve resonators

may be chosen so as to enable spectral characteriza-

tion of a single ferrite sample from 800 MHz to

25 GHz.

In the absence of an applied static ﬁeld, the ferrite

in the demagnetized state is isotropic and is described

Figure 1

Ferrite employed as dielectric resonator in a parallel plate waveguide.

Figure 2

Dielectric resonator system for broadband microwave permeability measurements.

172

Ferrite Cer amics at Microwave Frequencies

by a scalar frequency- and temperature-dependent

relative permeability and complex relative permittiv-

ity. The resonators are coupled to the external mi-

crowave source through two loop-terminated coaxial

cables that are adjustable so that the measured loaded

Q factor is equal to the unloaded Q factor within any

prescribed accuracy.

The measurement procedure follows several steps.

First, the complex permittivity of the ferrite is de-

termined with a TM

0n0

cavity. Second, the complex

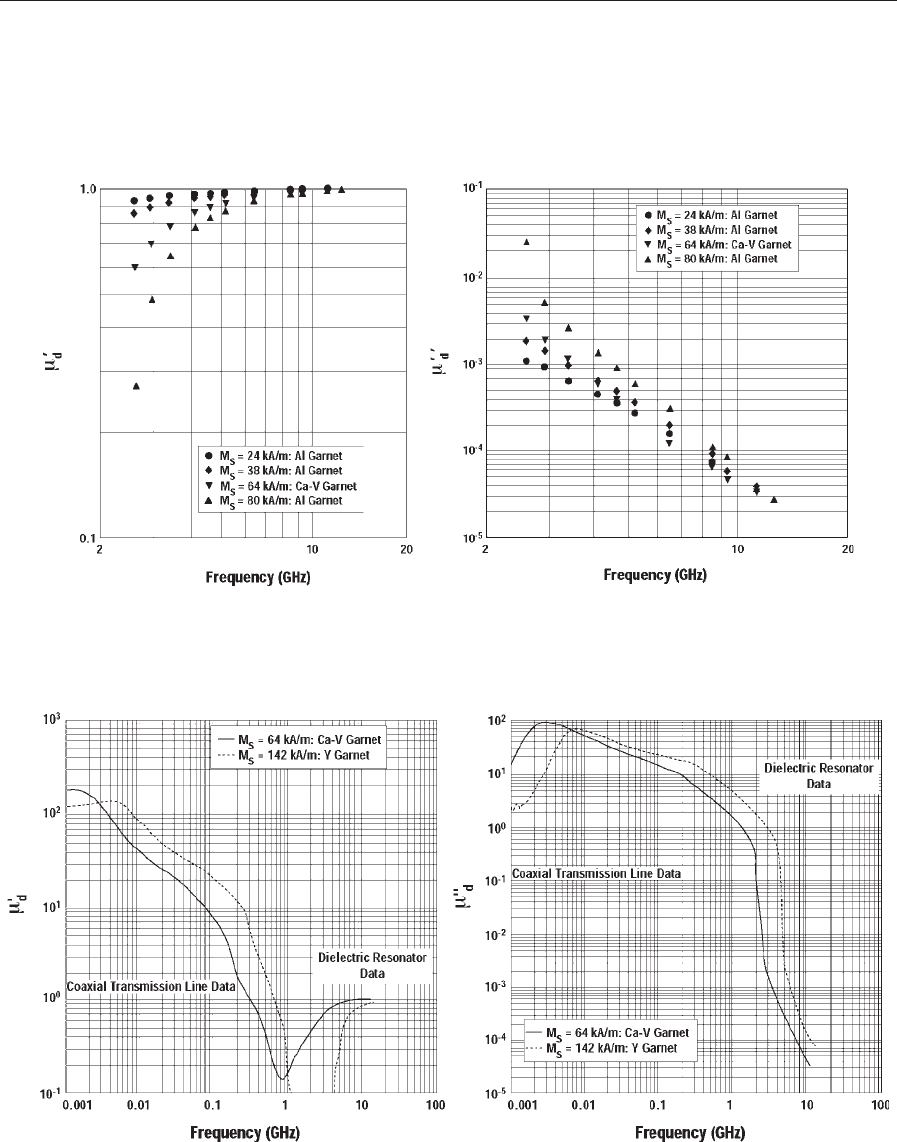
Figure 3

Measured complex permeability, m

, as a function of frequency for various doped garnets having differing saturation

magnetizations. T ¼297 K.

Figure 4

Broadband magnetic permeability spectra of demagnetized ferrite above and below magnetization frequency.

173

Ferrite Cer amics at Microwave Frequencies

relative permittivity of each dielectric ring resonator

is found from measurements of the resonant frequen-

cy and unloaded Q-factor of the empty ring resona-

tors operated in the TE

011

mode, taking into account

conductive microwave losses of the upper and lower

metal ground planes. The scalar permeability m

(f, T)

at frequency f and temperature T is determined from

measurements of the resonant frequency of the ring

resonator with ferrite specimen inserted and solving

the TE

011

eigenvalue equation (Geyer in prepara-

tion).

After determining m

, the magnetic loss index m

found as a solution to the equation:

þ p

tand

e;s

þ p

tand

þ p

tand

ð2Þ

where Q is the unloaded Q-factor for the TE

011

mode,

is the Q-factor reﬂecting conductor losses in the

metal plates, p

is the electric energy ﬁlling factor of

the dielectric sleeve resonator, p

, p

are the ferrite

sample electric and magnetic energy ﬁlling factors,

tand

e,s

and tand

are the dielectric loss tangents of the

sleeve resonator and ferrite sample, and tand

is the

magnetic loss tangent of the ferrite. Example complex

permeability data for garnets doped with aluminum

and calcium-vanadium are given in Fig. 3. Estimated

total uncertainty in 

is 1% and in 

is 2 10

5

These data clearly show the shift in magnetization

frequency to higher frequencies as saturation mag-

netization increases, as well as rapidly increasing

nonlinear magnetic losses as the magnetization fre-

quency is approached. Dielectric resonator and trans-

mission line data may be combined to yield accurate

complex permeability spectra of ferrite ceramics over

ﬁve decades in frequency (Fig. 4).

When a tuning bias is applied so that the ferrite

specimen is partially saturated, two dielectric low-loss

sleeve resonators having the same height but differing

diameters may be used to evaluate the complex tensor

permeability components (Krupka 1991, Geyer et al.

1998). In this case, two circularly polarized, oppo-

sitely rotating HE

111

and HE



111

resonant modes are

used with one sleeve for evaluating m

and m

, and the

011

resonant mode with the second sleeve is used

for m

. The aspect ratios of the sleeves are chosen so

that, for the nominal measurement frequency of in-

terest, all three resonant modes for both sleeves with

ferrite sample insertion occur at the same frequency

with zero bias ﬁeld. For this case, the tensor magnetic

properties are evaluated as a function of tuning bias

(Geyer et al. 1998)

2. Summary

Comparisons between experimentally evaluated de-

magnetized real permeability spectra of ferrites and

quasi-static theoretical formulations given by Schlo

mann (1970) have been reported (Green and Sandy

1974, Le Roux et al. 1988, Geyer 1999). These com-

parisons show good agreement when f

/fo0.75. The

effect of cooling magnesium spinel ferrite ceramics on

both dielectric and magnetic losses at microwave fre-

quencies has also been studied (Geyer 1999) using

dielectric resonator techniques. Generally, dielectric

losses of a ferrite ceramic decrease as the specimen is

cooled, albeit with increasing magnetic loss and de-

creasing magnetic permeability. Hence, with cooling,

the same ferrite ceramic may be used in microwave

tuning devices at higher frequencies.

Accurate magnetic characterization from 2 GHz to

25 GHz of a single ferrite specimen can be accom-

plished with low-loss dielectric sleeve resonators,

and combined with transmission line measurements

to reveal both low-frequency, high-loss and high-

frequency, low-loss properties.

See also: Ferrites; Ferrite Magnets: Improved

Performance

Bibliography

Baker-Jarvis J, Janezic M D, Grosvenor J H, Geyer R G 1993

Transmission reﬂection and short-circuit line methods for

measuring permittivity and permeability. Nat. Inst. Stand.

Tech. Tech. Note 1355-R

Bussey H E, Steinert L A 1958 Exact solution for a gyromag-

netic sample and measurements on a ferrite. IRE Trans. Mi-

crowave Theory Tech. MTT-6, 72–6

Courtney W E 1970 Analysis and evaluation of a method of

measuring the complex permittivity and permeability of mi-

crowave insulators. IEEE Trans. Microwave Theory Tech.

MTT-18, 476–85 1970

Geyer R G 1999 Complex permittivity and permeability of fer-

rite ceramics at microwave frequencies. Dielectric Ceram.

Mater., Ceram. Trans. 100, 195–215

Geyer R G Theoretical analysis of sleeve resonators for dielec-

tric and magnetic measurements of rod specimens. Nat. Inst.

Stand. Tech. Note In preparation

Geyer R G, Jones C, Krupka J 1998 Complex permeability

measurements of ferrite ceramics used in wireless communi-

cations. Dielectric Ceram. Mater., Ceram. Trans. 88, 93–113

Green J J, Kohane T 1964 Testing of ferrite materials for mi-

crowave applications. Semicond. Prod. Solid State Technol. 7,

46–54

Green J J, Sandy F 1974 Microwave characterization of par-

tially magnetized ferrites. IEEE Trans. Microwave Theory

Tech. MTT-22, 641–5

Krupka J 1991 Measurements of all complex permeability ten-

sor components and the effective line widths of microwave

ferrites using dielectric ring resonators. IEEE Trans. Micro-

wave Theory Tech. 39, 1148–57

Krupka J, Geyer R G 1996 Complex permeability of demag-

netized microwave ferrites near and above gyromagnetic res-

onance. IEEE Trans. Magn. 32, 1924–33

LeGraw R C, Spencer E G 1956 Tensor permeabilities of fer-

rites below magnetic saturation. IRE Con. Rec. 5, 66–74

Le Roux P, Jecko F, Forterre G 1988 Nouvelle methode de

determination des parties reeles des parametres electriques et

magnetiques des resonateurs a ferrites satures et non satures.

Ann. Telecommun. 43, 314–22

174

Ferrite Cer amics at Microwave Frequencies

Muller-Gronau W, Wolff I 1983 A microwave method for the

determination of the real parts of the magnetic and dielectric

material parameters of premagnetized microwave ferrites.

IEEE Trans. Microwave Theory Technol. MTT-32, 377–82

Ogasawara N, Fuse T, Inui T, Saito I 1976 Highly sensitive

procedures for measuring permeabilities (m

) for circularly

polarized ﬁelds in microwave ferrites. IEEE Trans. Magn.

MAG-12, 256–9

Schlo

mann E 1970 Microwave behavior of partially magnetized

ferrites. J. Appl. Phys. 41, 204–14

R. G. Geyer

National Institute of Standards and Technology

Boulder, Colorado, USA

Ferrite Magnets: Improved Performance

Ferrite magnets, based on the compound AFe

(A ¼Sr, Ba) and the magnetoplumbite or M crystal

structure, have a dominant position on the magnet

market (57% by value and 95% by weight), thanks to

the favorable performance/price ratio. The main ap-

plication for high-grade ferrite magnets is as segments

in various d.c. motors for the automotive industry.

Their market share would be even larger if their

magnetic performance, notably remanence B

and

coercivity H

, could be further improved. This can

no longer be expected from the conventional tech-

nology, which has almost attained its saturation. In

recent years, however, it has been recognized that

LaCo or related substituents may lead to significantly

improved performance. This has initiated a renais-

sance of its basic research as well as a new generation

of high-performance ferrite magnets. After a short

survey of the conventional ferrite magnets, the new

LaCo–M ferrites are discussed, referring to a recent

more extended review article (Kools et al. 2002).

1. Conventional Ceramic Ferrite Magnets

The manufacturing process of ceramic ferrite mag-

nets is a classical ceramic process (see Alnicos and

Hexaferrites), having several specific features (Ko-

jima 1982, Kools 1992). Most characteristic are the

wet pressing in a magnetic ﬁeld to align the powder

particles in order to obtain high remanence, the ﬁne

milling into alignable particles of B1 mm, the natural

tendency to lateral grain growth (platelet-shaped

crystals), and, ﬁnally, the necessity to keep the ﬁred

grains small to obtain high coercivity.

In the 1970s and 1980s it became gradually clear

that increased magnetic performance can only be at-

tained by further decreasing the particle size of the

milled powders. This implies increased milling effort

and more difﬁcult wet pressing, two factors which

largely contribute to the production costs. This has

led to the following definition of the magnetic per-

formance IP in terms of remanence (B

) and co-

ercivity (H

): IPðmTÞ¼B

þ0:4m

. It is governed

uniquely by the particle size obtained after milling.

For technical and economical reasons, however, there

is a lower limit for the latter particle size. The cor-

responding upper performance level of IP E550 mT

characterizes the saturation state of the conventional

technology in the early 1990s.

1.1 Intrinsic Properties

The intrinsic properties stem from the M-crystal

structure and, notably, from the ﬁve distinct Fe-

sublattices, coupled by superexchange. Two intrinsic

properties are crucial: the saturation magnetization

) determines B

and the magneto-crystalline an-

isotropy ﬁeld strength (H

) determines H

The magnitude of J

derives from the mutual

orientations of the ﬁve Fe-sublattice moments, as

given by the Gorter model: the moments at 2a, 12k,

and 2b are mutually parallel and antiparallel to the

moments at 4f1 and 4f2. This model is supported by

magnetization measurements, Mo

ssbauer spectrome-

try, and, recently, also by ab initio calculation (Fang

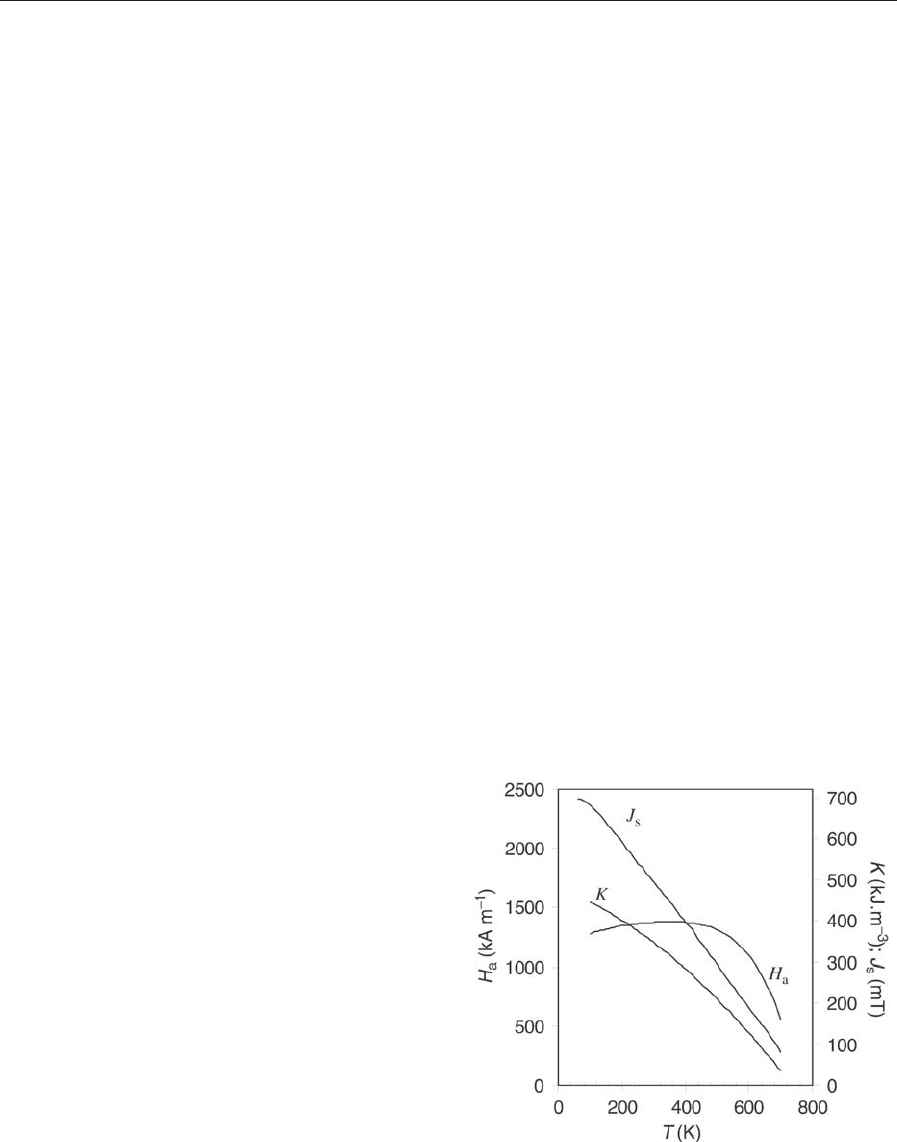
et al. 2003). The J

2T curve (Fig. 1) is almost linear

in the room temperature region with dJ

/dT ¼

0.9 mT K

1

The anisotropy ﬁeld H

represents the hypothetical

ﬁeld that would be able to align the magnetization

perpendicular to the easy direction, the c-axis. It is

deﬁned by H

¼ 2K

, where the anisotropy con-

stant K

characterizes the associated anisotropy en-

ergy. The origin of K

is related to spin–orbit

Figure 1

Temperature dependence of J

, K, and H

for BaM.

175

Ferrite Magnets: Improved Performance

coupling at the 2b and 12k sites, but a detailed model

is still lacking. The K

2T curve is analogous to the

2T curve, but less curved at low temperature, re-

sulting in a ﬂat H

2T curve with dH

=dTE0at

room temperature (Fig. 1).

1.2 Modeling B

and H

The formulas given below refer to medium- and high-

grade ferrite magnets in which the grains are sup-

posed to be single domain in the remanent state and

magnetization reversal inside the grains is supposed

to be governed by domain nucleation.

The remanence is described by the formula

¼ kJ

¼ fd=d



ð1Þ

The factor k takes account of the inﬂuence of the

microstructure. It consists of three contributions:

the degree of alignment f (0.5ofo1), the amount of

M-phase s, and the relative density d=d

. Typical

values for (unsubstituted) high-performance magnets

¼420 mT) are: f ¼0.92, d=d

¼0.98, s ¼0.98

(k ¼0.88). The (relative) temperature coefﬁcient of

the remanence, TCðB

Þ, derives from the temperature

coefﬁcient of the saturation magnetization, TCðJ

Þ,

and amounts to 0.19% for nonsubstituted grades.

The coercivity is described by the expression

¼aH

ðN

ÞðB

þ J

¼aH

ðN=m

Þðk þ 1ÞJ

ð2Þ

Its dependence on the microstructure is described by

k and, in particular, by the factors a and N. The

factor a increases with decreasing grain size, thus re-

ﬂecting the well-known H

-grain size dependency.

The factor N is governed by the grain shape and in-

creases when the grains become more platelet shaped.

For an unsubstituted high-grade magnet (H

270 kA m

1

), typical microstructural factors are: a ¼

0:52 and N ¼ 0:7. The value of TCðH

Þ is easily

derived from Eqn. (2) by differentiation. Substituting

the typical values given above, one obtains

TCðH

ÞE þ 1kAm

1

or E0:4% K

1

1.3 Substitutions

Until recently, it seemed impossible to improve the

magnet performance by means of substitutions. The

can be increased, indeed, but only at the costs of

and vice versa. Only the substitution of Al and/or

Cr for Fe has been of practical importance, including

a decreased J

at constant K

, thus leading to in-

creased H

and H

1.4 Microstructure

Grain growth and platelet grain shape should be

suppressed during high-density sintering, otherwise

the H

deteriorates. Si-based additions are common-

ly applied. As the underlying mechanism, the reaction

induced grain growth inhibition (RIGGI) has been

put forward, being related to the slow incorporation

of silica.

2. LaCo-type Substituted M-ferrite Magnets

Scattered over the period 1959–1996, several studies

have been published, that included occasionally

LaCo-M-type compositions, corresponding to the

general formula A

1x

12x

(ARB-M),

where A ¼ Ba; Sr; y,R¼ La

3þ

,Pr

3þ

,Bi

3þ

; y, and

B ¼ Co

2þ

,Ni

2þ

,Fe

2þ

,y. The recent recognition that

LaCo-type ferrite magnets can represent a new gen-

eration of high-performance ferrite magnets has

provoked a wave of investigations, being initially

practically oriented in order to secure patent rights

(Taguchi et al. 1998, Takami et al. 1999). The results

obtained share the following general features:

increased performance (IPE600 mT), notably

from increased H

, but B

may vary;

reduced TCðH

Þ, down to B50% of the un-

sbstituted value;

wide composition range ARB-M, including also

ðFe þ BÞ=ðA þ RÞa12 with optimum properties for

SrLaCoM ðxE0:25Þ, where Co may be partly re-

placed by Fe

2 þ

; and

classical processing: only the calcination time is

longer than usual.

These promising results have provoked an inten-

sive study as to the precise effects and their back-

grounds. This is briefly reviewed below, based on our

own studies.

2.1 Effects on the Magnet Properties

The main effects illustrated in Figs. 2–5 show the

following:

a significant increase of H

up to x ¼ 0:25

ð25%Þ, followed by a similar decrease for

0:25oxp0:4;

reduced TCðH

Þ (50% for x ¼0.3);

slight increase of B

(3.5% for x ¼0.4); and

moderate squareness of the demagnetization

curve, which strongly deteriorates for high xðx40:2Þ.

These effects refer to SrLaCo-M, but analogous

effects are found for BaLaCo-M.

2.2 Background of the Effects

The coercivity is explained on the basis of the

coercivity model (Eqn. (2)), where an increased H

value is substituted (Fig. 3), as measured by single

176

Ferrite Ma gnets: Improved Performance

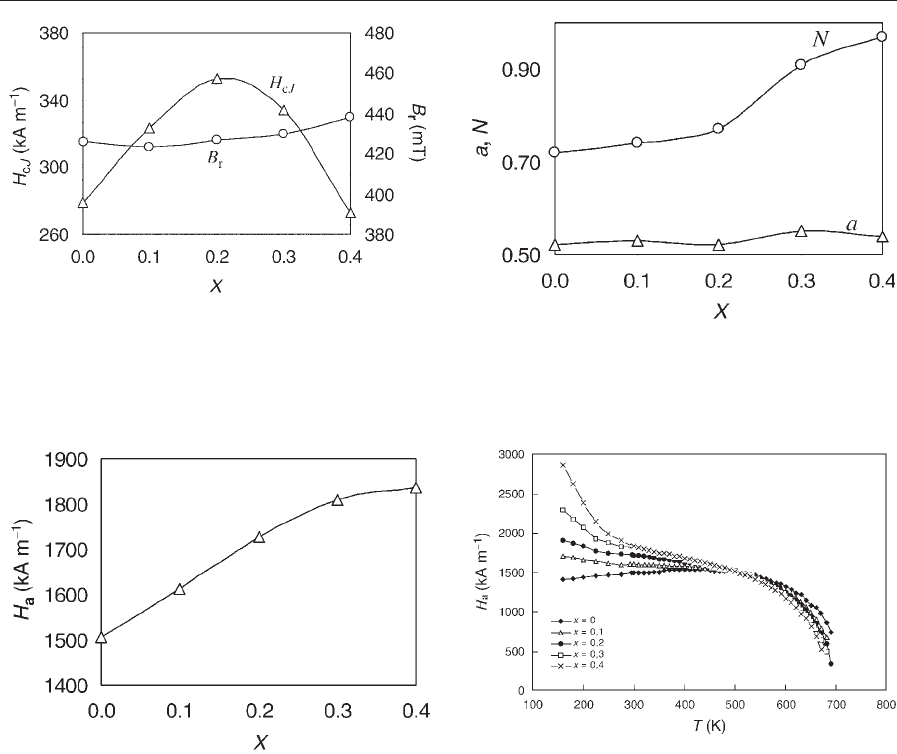
point detection (SPD) H

measurements (see Mag-

netic Measurements: Pulsed Field ). Since the values

for B

, a, and N (Fig. 4) appear to be quite normal,

the increased H

is dominated by the increased H

The decrease of H

for x40:25 stems from the

more pronounced platelet shape. The microstructure

parameters a and N were measured both magnetically

and by SEM observation. For x40:25 the N value

increases sharply (Fig. 4), while the a value remains

essentially constant, thus explaining the drop in H

The TCðH

Þ is explained by the same coercivity

model in the differential form, substituting apart

from the experimental a and N values, the measured

values for dJ

=dT and dH

=dT (Fig. 5). This for-

mula explains that TCðH

Þ deviates significantly

from the usual one: dH

=dT is no longer close to zero

as usual, but has become negative, resulting in a de-

creased TCðH

Þ.

The explanation of B

is based on Eqn. (1) and

separate measurements of f, ðd=d

Þ, and s . The factor

sð300 KÞ

is decomposed into two factors: J

sð0KÞ

and a

new parameter R

¼ J

sð300 KÞ

sð0KÞ

characterizing

the curvature of the J

2T curve. Density and J

sð0KÞ

appear to be constant; so the slight increase of B

dominated by the alignment factor ( f ) and the cur-

vature factor ðR

Þ, both showing a slight increase

(Fig. 6).

The poor squareness was attributed to chemical

and microstructural inhomogeneities. Mo

ssbauer

analysis and resistivity measurements showed that

the Co substitution is not complete, Co being partly

Figure 2

and B

vs. x for Sr

1x

12x

magnets

(reproduced by permission of Kools et al. (2002) from

J. Magn. Magn. Mater., 242–245 (Part 2), 1270–6).

Figure 4

Microstructural factors underlying H

, measured

magnetically (Morel et al. 2000).

Figure 5

Low-temperature behavior of H

for

1x

12x

ðx ¼ 0:2Þ (reproduced by

permission of Gro

ssinger et al. (2000) from Ferrites,

Proc. Int. Conf. on Ferrites, ICF8, pp. 428–30).

Figure 3

SPD data for Sr

1x

12x

magnets showing

vs. x (Gro

ssinger et al. 2000).

177

Ferrite Magnets: Improved Performance

replaced by Fe

2 þ

. The strong deterioration of the

squareness for x40:2 was related to a bimodal grain

size distribution.

2.3 Intrinsic Aspects

Substituted M-ferrite magnets are single phase for

0oxo0.35. The cell constant a remains constant,

whereas c decreases slightly and linearly up to x ¼0.4.

The latter holds also for T

The analogy between Sr and Ba compounds points

to Co as the active ion. The Co sublattice occupation

was studied by various techniques, but all being at the

limit of detection. The provisional conclusion is that

2 þ

/Co is at 2a and Co at 4f

. For CoTi substituted

M-ferrites and related compounds, Co prefers other

sites and acts negatively on the anisotropy (Kojima

1982). Apparently, the excess charge of La and its

ﬁxed position on the Ba sites forces Co to a special

site, where it can contribute to the anisotropy.

The increase of H

(obtained from SPD data) with

increasing x is due to an increase of the magneto-

crystalline anisotropy K

. In addition, H

increases

further when T decreases, similar to LaFe

2 þ

(Lotgering 1974). In view of that, a similar mechanism

is assumed: the increased K

stems from the single-ion

contribution of Fe

2 þ

/Co at 2a and Co at 4f

2.4 Microstructural Aspects

There are three major effects: (1) The grain size after

calcination decreases with x, (2) the grain size after

ﬁring and the platelet grain shape increase with x,

and (3) the microstructure becomes more nonuniform

when x increases. The ﬁrst effect is related to incom-

plete substitution of LaCo during calcining, thus

provoking RIGGI from LaCo. The second effect is

also related to the incomplete calcination by means of

which Co remains in the secondary phase and coun-

teracts during sintering the RIGGI from silica (Kools

et al. 2001). The third effect is related to the ﬁrst one.

By optimizing the chemical homogeneity (decreased

particle size of the LaCo raw materials) and decreas-

ing the Co/La, ratio, the squareness could be restored

to the unsubstituted level (Morel and Tenaud 2002).

3. Concluding Remarks

LaCo-type substituted ferrite magnets can be de-

scribed by the classical models for M-ferrite magnets,

having as a characteristic feature the increased mag-

neto-crystalline anisotropy at 300 K and its increased

temperature dependence.

The increased H

and reduced TC(H

) of LaCo-

type ferrite magnets allow new applications. Due to

the more expensive raw materials (La, Co), the costs

are somewhat higher, but optimization will certainly

lead to cost reduction. It is expected that the new

LaCo-type ferrite magnets will acquire a significant

market share in the near future, notably for starter

motors and small motors.

See also: Coercivity Mechanisms; Magnetic Hyster-

esis; Magnetic Materials: Hard; Magnets, Soft

and Hard: Domains; Magnets: High-temperature;

Magnets: Sintered

Bibliography

Carbone Lorraine commercial data book 2002: www.

Ferroxdure.com

Fang C M, Kools F, Metselaar R, de With G, de Groot R A

2003 Magnetic and electronic properties of strontium hexa-

ferrite SrFe

from ﬁrst-principles calculations. J. Phys.

Condens. Matter (submitted)

Ferrites 2000 Proc. 8th International Conference on Ferrites,

ICF8. Jap. Soc. Powder and Powder Metallurgy, Kyoto,

Japan

Gro

ssinger R, Tellez Blanco J C, Kools F, Morel A, Rossignol

M, Tenaud P 2000 Anisotropy and coercivity of M-type Ba

and Sr-ferrites containing La and Co. In: Ferrites, Proc. Int.

Conf. on Ferrites, ICF8, Kyoto 2000, pp. 428–30

Iida K, Minachi Y, Masuzawa K, Kawakami M, Nishio H,

Taguchi H 1999 High-performance ferrite magnets: M-type

Sr-ferrite containing Lanthanum and Cobalt. J. Magn. Soc.

Japan. 23, 1093–8

Kojima H 1982 Fundamental properties of hexagonal ferrites.

In: Wohlfarth 1982, Chap. 5, pp. 305–91

Kools F 1992 Hard magnetic ferrites. In: Bever M B (ed.) En-

cyclopedia Mater. Sci. and Eng (2nd edn.) Pergamon Press,

Oxford, UK

Kools F, Morel A, Tenaud P 2001 LaCo-substituted ferrite

magnets: increased coercivity and improved microstructure.

In: Euro PM2001, Proc. European Powder Metallurgy Con-

gress. Nice, France, Vol. 2

Figure 6

Remanence factors vs. x for Sr

1x

12x

magnets (reproduced by permission of Kools et al.

(2002) from J. Magn. Magn. Mater., 242–245 (Part 2),

1270–6).

178

Ferrite Ma gnets: Improved Performance

Kools F, Morel A, Gro

ssinger R, LeBreton J M, Tenaud P

2002 LaCo-substituted ferrite magnets, a new class of high-

grade ceramic magnets: intrinsic and microstructural aspects.

J. Magn. Magn. Mater. 242–245 (Part 2), 1270–6

Lotgering F K 1974 Magnetic anisotropy and saturation of

LaFe

and some related compounds. J. Phys. Chem.

Solids. 35, 1633–9

Morel A, Tenaud P 2002 International Patent Applications (1)

WO 02/085810 A1 and (2) pending

Morel A, Kools F, Tenaud P, Gro

ssinger R, Rossignol M 2000

Modelling of LaCo substituted M-type ferrite coercivity. In:

Ferrites, Proc. Int. Conf. on Ferrites, ICF8, Kyoto 2000, pp.

434–6

Morel A, LeBreton J M, Kreisel J, Wiezinger G, Kools F,

Tenaud P 2001 Sublattice occupation in Sr

1x

12x

hexagonal ferrite analysed by Mo

ssbauer

spectrometry and Raman spectroscopy. J. Magn. Magn.

Mater. 242–248, 1405–7

Pieper M, Kools F, Morel A 2002 NMR characterization of

Co-sites in La þCo Sr hexaferrites with enhanced magnetic

anisotropy. Phys. Rev. B 65 (184402), 1–5

Taguchi H, Iida K, Masuzawa K, Minachi Y 1998 Eur. Patent

Application EP 0 905 718 A1

Takami H, Kubota Y, Ogata Y 1999 Eur. Patent Application

EP 0 964 411 A1

Wiezinger G, Mu

ller M, Gro

ssinger R, Pieper M, Morel A,

Kools F, Tenaud P, LeBreton J M, Kreisel J 2002 Substituted

ferrites studied by nuclear methods. Phys. Stat. Sol. (a) 189

(2), 499–508

Wohlfarth E P (ed.) 1982 Ferromagnetic Materials North-

Holland, Amsterdam, Vol. 3

F. Kools

Carbone Lorraine-Ferrites, Evreux, France

A. Morel

St Pierre d’Allevard, France

Ferrites

Since their commercial introduction in 1948 by Phi-

lips, soft ferrites have found widespread use in elec-

tronic applications as inductor or transformer cores,

because of their high resistivity in comparison to

metallic soft-magnetic materials. This makes soft-

magnetic ferrites considerably better suited for appli-

cations at frequencies X10 kHz. Soft-magnetic ferrites

belong to the class of ferrites which have a cubic,

spinel lattice structure. These ferrites have the struc-

tural formula MeFe

with Me being a divalent

metal ion from the 3d transition elements: manganese,

iron, cobalt, nickel, copper, zinc, or combinations of

these. In addition, also other ions such as Li

,Mg

2 þ

3 þ

,Ti

4 þ

,orSb

5 þ

can be incorporated in the spinel

lattice. There is also a class of soft-magnetic ferrites

with a hexagonal crystal structure, which has soft-

magnetic properties. However, this class of soft fer-

rites has found limited application thus far, and is not

treated here. The reader is referred to the treatise by

Smit and Wijn (1959).

The spinel-type lattice structure characterizing the

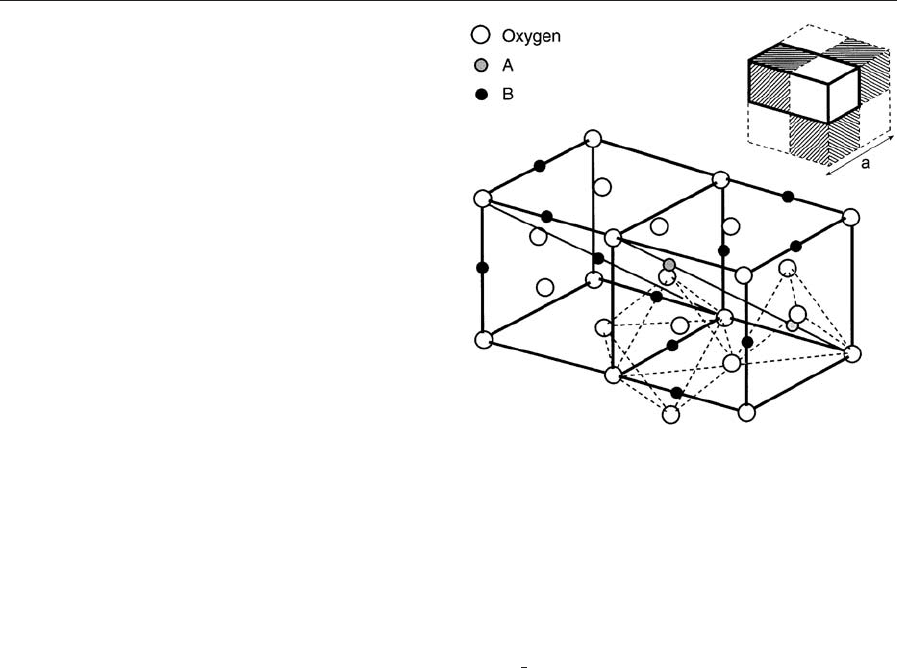
conventionally applied ferrites is depicted in Fig. 1.

This lattice structure has a lattice parameter a in the

range 8.30–8.50 A

depending on the composition of

the ferrite (Smit and Wijn 1959). In the unit cell, of

which

is drawn in detail in Fig. 1, the oxygen ions

(O in Fig. 1) form a close-packed face-centered cubic

lattice. There are 64 possible tetrahedral (or A) and

32 possible octahedral (or B) interstices or sites in

which metal ions can be incorporated. Only eight of

the octahedral and 16 of the tetrahedral sites are ﬁlled

with metal cations. The magnetic interactions are

such that the two neighboring magnetic ions on the

B-site are ferromagnetically (that is parallel) coupled,

whereas the much larger coupling between the mag-

netic ion on the A-site and the ions on the B-sites is

antiferromagnetic (antiparallel). Since, there are two

ions antiparallel coupled to each magnetic ion on the

A-site, a net magnetic moment still results.

This gives rise to the so-called ferrimagnetism, a

net magnetic moment in a magnetic material in which

the dominant magnetic interaction is antiferromag-

netic. This behaviour can be understood on the basis

of super exchange interaction between the magnetic

ions as explained by Anderson (1963) and Good-

enough (1963).

As shown in Fig. 1 the magnetic ions in ferrites are

separated by oxygen ions, which precludes a direct

exchange interaction between the magnetic ions.

Since, in addition, ferrites are insulators (or very

poor semiconductors) exchange interaction by itiner-

ant electrons is also not possible. The explanation for

Figure 1

The spinel lattice structure.

179

Ferrites