Buschow K.H.J. (Ed.) Concise Encyclopedia of Magnetic and Superconducting Materials

Подождите немного. Документ загружается.

magnetoresistance and temperature-dependent resis-

tivity in ﬁxed ﬁelds, and are found to agree with

earlier studies.

2.2 Erbium

This introduction to the magnetic phase diagrams of

erbium forms an overview, and the reader is encour-

aged to follow the references below for more detail of

this fascinating element.

The magnetic phase diagrams for the c (McMor-

row et al. 1992) and a-axes (Jehan et al. 1994) are

presented in Figs. 2(b) and 2(c). When compared with

thulium, it is clear that erbium has a greater number

of magnetic structures and, unlike thulium, a moment

develops parallel to the a-axis. However, as with

thulium and other heavy rare earths, the structures

are modulated along the c-axis. Where fractions ap-

pear in each of these ﬁgures, the denominator rep-

resents the fundamental periodicity. In the region

marked CAM, the periodicity is similar to that ob-

served for thulium of Q ¼2/7c*.

Referring to Fig. 2(b), there appears a region sep-

arated and marked by ‘‘2/7’’; this region of the phase

diagram differs in that a moment has developed

along the a-axis at these temperatures and ﬁelds,

and this is also reﬂected in the a-axis phase diagram

(Fig. 2(c)). In both ﬁgures there are regions marked

‘‘INC,’’ and these regions are described as incom-

mensurate. This refers to the fact that the modulation

wave vector parallel to the c-axis bears no simple re-

lation to the crystal lattice. In the a-axis phase dia-

gram (Fig. 2(c)) there are three other terms. These are

‘‘cone,’’ ‘‘fan,’’ and ‘‘ferromagnetic.’’ They all refer to

the orientation of the moment parallel to the a-axis,

since the moments parallel to the c-axis are aligned

ferromagnetically. The ‘‘cone’’ phase refers to the

structure in which the moments are parallel to both

the a-axis and the b-axis. These moments are ar-

ranged in a helix about the c-axis, which, when pro-

jected onto a single lattice point, would appear as a

‘‘cone.’’ The term ‘‘fan’’ is used to describe a struc-

ture in which the moments on the a-axis have pro-

jected moments aligned parallel to the a-axis, but

from one site to the next the angle of tilt away from

the a-axis varies. When this arrangement of moments

is projected onto a single lattice position, the mo-

ments appear to make a ‘‘fan’’ pattern parallel to the

a-axis. The ‘‘ferromagnetic’’ phase has all the mo-

ments parallel to the a-axis.

For both phase diagrams there is a region between

TB20 K and 55 K, and in this temperature range

there is a host of structures. These structures are col-

lectively known as ‘‘cycloidal’’ structures (Cowley

and Jensen 1992), and may be ‘‘viewed’’ as moments

modulated along the c-axis, forming an ellipse with

the major axis parallel to the c-axis and the minor

axis along the a-axis. This is an extremely difﬁcult

series of structures to visualize, and the reader is re-

ferred to Cowley and Jensen (1992), for a complete

description.

Having outlined the magnetic phase diagrams ob-

tained from neutron diffraction experiments, it is now

possible to consider the results of magnetoresistance.

There are two ﬁgures, presenting the effects of mag-

netic ﬁeld for two crystal directions.

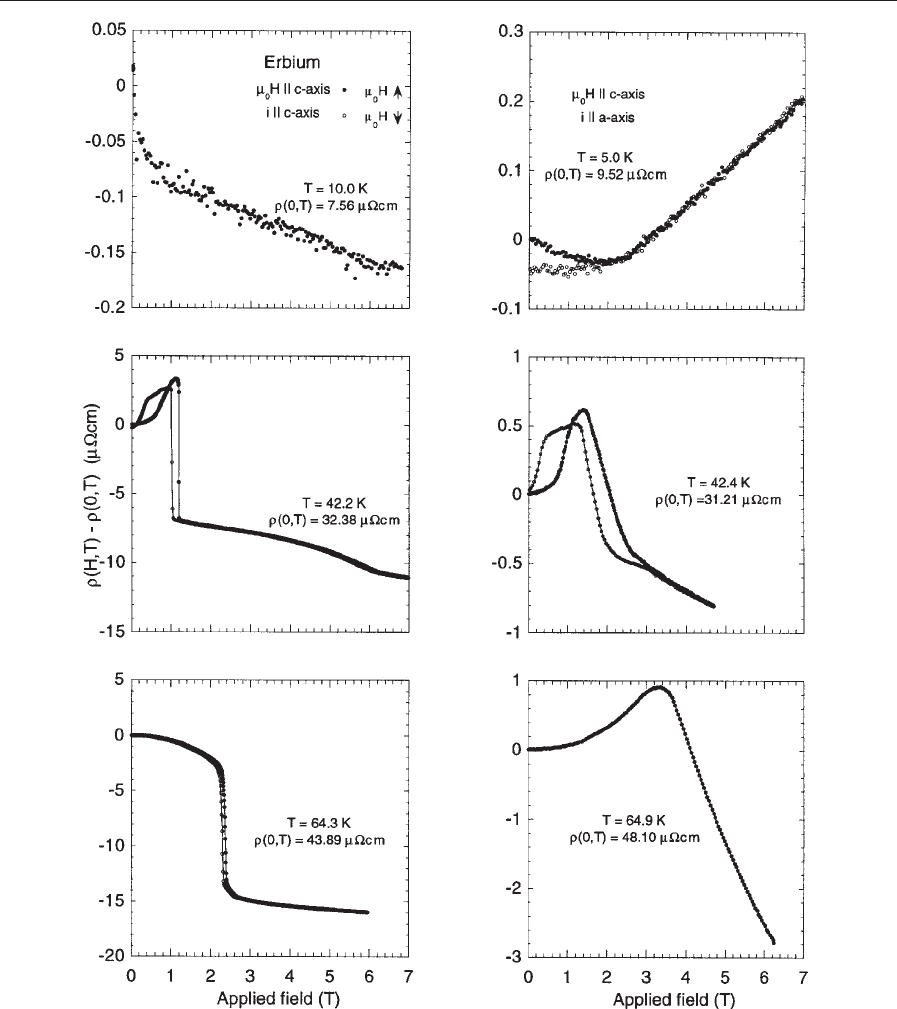
Figure 4 presents the results for the ﬁeld parallel to

the c-axis and measurement of the resistivity parallel

to the c-axis (longitudinal c-axis on left) and parallel

to the a-axis (transverse a-axis on right). For

T ¼10 K, erbium is in the ‘‘cone’’ phase, and for

the longitudinal geometry there is a small decrease in

the resistivity at low ﬁelds, associated with the re-

moval of magnetic domains. As the ﬁeld increases,

there is a linear decrease associated with the suppres-

sion of spin ﬂuctuations (Yamada and Takada 1973).

In the transverse geometry at T ¼5 K, the resistivity

at ﬁrst decreases as spin ﬂuctuations are frozen.

However, at approximately 2 T, the magnetoresist-

ance increases linearly resulting from the Lorentz

force (Pippard 1989) acting on the motion of the

electrons in the applied magnetic ﬁeld. At T ¼42.2 K,

the longitudinal measurement reveals several fea-

tures. For ﬁelds less than 1.2 T, the magnetoresistance

increases, revealing two regimes: 0-0.4 T and 0.4-

1.2 T. These regimes accord well with the passage

through 3/11c* and 2/7c* phases.

The behavior in both may be viewed from the per-

spective outlined by Yamada and Takada (1973), in

which the moments antiparallel to the applied ﬁeld

are being turned in the ﬁeld. At 1.2 T there is a large

decrease in the resistivity passing from the 2/7c*

phase to the incommensurate phase (INC). This is

interpreted as the removal of the superzone bound-

aries and the consequent replacement of Fermi sur-

face (Elliott and Wedgwood 1963). Above 1.2 T, the

moments of the incommensurate phase collapse

smoothly about the c-axis, until at 6.2 T erbium en-

ters the ferromagnetic phase. The transverse meas-

urement at this temperature is interesting in that the

behavior is very similar. This suggests that at this

temperature there is strong coupling of the spin ﬂuc-

tuations along each axis. For T ¼64.3 K, the mag-

netic structure is similar to that observed for thulium,

with a CAM arrangement of the moments, and the

dominant term in the anisotropy is that which ‘‘pre-

fers’’ the c-axis. The behavior at this temperature is

described by the same argument used for thulium at

T ¼53 K, and this represents the ﬁrst appearance of

‘‘canonical’’ behavior in the magnetoresistance for

these two different elements.

Figure 5 shows the inﬂuence of the magnetic ﬁeld

on the a-axis resistivity. The graphs on the left rep-

resent the longitudinal a-axis magnetoresistance, and

those on the right represent the transversal c-axis re-

sistivity. For the longitudinal magnetoresistance at

T ¼4 K, there is a steady increase of resistivity in the

160

Elemental Rare Earths: Magnetic Structure and Resistance, Correlation of

‘‘cone’’ phase, consistent with the Lorentz force dis-

torting the motion of the electrons (Pippard 1989).

This is observed for both geometries. When the mo-

ments ﬂip into the ‘‘fan’’ phase, there is a removal of

Fermi surface. As the magnetic ﬁeld increases there is

smooth collapse of the ‘‘fan,’’ formed by moments on

the a- and the b-axes, onto the a -axis. There is no

model for this process of moment collapse coupled

Figure 4

Magnetoresistance for erbium B8c-axis. Longitudinal c-axis on the left and transverse a-axis on the right. The symbols

(*) and (J) represent increasing ﬁeld and decreasing ﬁeld, respectively.

161

Elemental Rare Earths: Magnetic Structure and Resistance, Correlation of

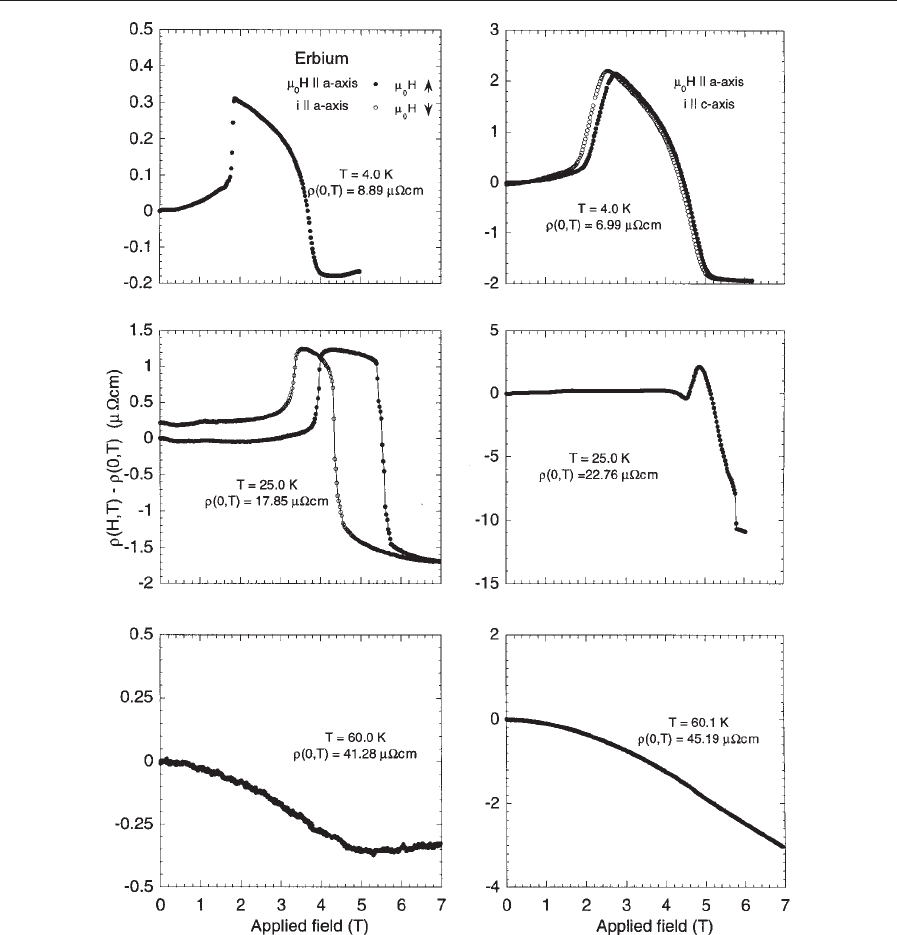
with a change in Fermi surface. Theoretical consid-

eration of the results for erbium (Ellerby et al. 2000)

has found that there are gaps in sections of the Fermi

surface normal to both the a and c-axes, and this is

certainly responsible for the decrease of the resistivity

in the transverse c-axis above 5 T. This replacement

of Fermi surface arises from the fact that a ﬁeld par-

allel to the a-axis eventually drives erbium to a fully

ferromagnetic state, as indicated in the phase dia-

gram, and this in turn produces a modulation

Q ¼0c* and therefore G

¼0.

The temperature-dependent resistivity for erbium

in these two axes (Fig. 1) may be ﬁtted, using Eqn.

(4), with values for G which have a temperature de-

pendence (Ellerby et al. 2000), and values of G

0.71 and G

¼0.14 for m

H ¼0 T. The value of G

Figure 5

Magnetoresistance for erbium B8a-axis. Longitudinal a-axis on the left and transverse c-axis on the right.

162

Elemental Rare Earths: Magnetic Structure and Resistance, Correlation of

similar to that found for thulium, where the structure

is Q ¼2/7c*. At a temperature of T ¼25 K, the mag-

netoresistance remains unaffected along both axes

until 4 T, and thus the model of Yamada and Takada

(1973), does not apply. The resistivity increases

sharply at 4 T as erbium enters the Q ¼2/7c* phase,

this being in accordance with the removal of a por-

tion of the Fermi surface. As the ﬁeld is increased

further, there is a sharp decrease in both geometries

as erbium enters the ferromagnetic phase. As in the

case at 4 K, there is no modulation of the magnetic

moment, and consequently the superzone bounda-

ries cease to exist abruptly at this boundary, whilst

increasing the available Fermi surface. There is

significant hysteresis at this transition, suggesting a

ﬁrst-order transition. The results at T ¼60 K can

be understood through the model of Yamada and

Takada (1973), in which erbium is paramagnetic

along the a-axis, and therefore an applied ﬁeld sys-

tematically suppresses the spin ﬂuctuations along this

axis. This is consistent with the dominance of the

strong uniaxial anisotropy along the c-axis.

The summary of this section highlights the corre-

spondence of magnetic phase diagrams with the mag-

netoresistance of erbium. The experimental results

presented map well onto the magnetic phase dia-

grams; however, there are some differences worthy of

note. The most prominent derives from the effects of

the demagnetizing factor usually present in neutron

diffraction studies, which can be of the order 0.5,

whilst in longitudinal magnetoresistance the demag-

netizing factor can be less than 0.1. The factor results

in discrepancies of boundary position, and correc-

tions for this effect can be determined (Stoner 1945).

The low-temperature behavior of erbium is dominat-

ed by the motion of the conduction electrons in an

applied ﬁeld, with the effects of Fermi-surface mod-

iﬁcation superposed. A further aspect of phase dia-

grams concerns the nature of the phase transition.

The observation of hysteresis at a transition is a

strong indication of a ﬁrst-order transition, and this

can be important in some studies.

3. Concluding Remarks

The preceding sections presented a series of results

for the rare earths, chosen to exhibit different an-

isotropy and exchange. In both cases it has been

possible to apply some form of Eqn. (2), incorporat-

ing the superzone effects through Eqn. (4) as for the

c-axis of thulium and erbium. There is, however, one

proviso in the case of erbium. Eqn. (4) requires the

inclusion of a temperature dependence in G

which

represents the effects of the Fermi surface on the re-

sistivity (Ellerby et al. 2000). In addition to this, the

a-axis of erbium appears to lose a small portion of the

Fermi surface in the cycloidal phase. This is recov-

ered on entry into the cone phase at T ¼20 K (Fig. 1).

Indeed, Eqn. (2) is particularly versatile in its ability

to describe excitations in magnetic systems, and may

also be used to analyze systems exhibiting gaps in the

spin-wave spectrum.

There were two sets of canonical behavior ob-

served in the magnetoresistance. The ﬁrst concerned

the prominent correlation for the c-axis modulated

structures (CAM) of thulium and erbium. The second

was found in the magnetoresistance for the ‘‘fan’’

phase in erbium and exhibited in the a-axis measure-

ments a T ¼4 K. This behavior has also been ob-

served in the resistivity for the holmium b-axis in the

‘‘fan’’ phase, where there is quadratic collapse in the

resistivity associated with the collapse of the ‘‘fan.’’

These responses may be added to the schema derived

by Yamada and Takada (1973), to understand the

magnetoresistance in spin-ﬂop systems, and the in-

ﬂuence of spin/moment ﬂuctuations in ferromagnetic

and paramagnetic materials. In both systems dis-

cussed, the inﬂuence of the magnetic superzones

(Mackintosh 1962, Elliott and Wedgwood 1963,

Miwa 1963) was found to be of prime importance

in the study of the c-axis of these elements. This is

true for many of the heavy rare-earth elements.

In comparing results of magnetoresistance with

those of neutron diffraction studies, caution is re-

quired. In the neutron diffraction studies there is of-

ten a large contribution to the position of the phase

boundary coming from the demagnetizing ﬁeld. This

can lead to ambiguities. Furthermore magnetoresist-

ance, whilst being one of the most sensitive probes of

magnetic systems, can often fail to reveal subtle

changes in structural modulation; this is the case with

incommensurate structures. Magnetoresistance can

only assist in a qualitative fashion when composing

magnetic phase diagrams, and will provide allu-

sions as to the type of magnetic structure. However,

accurate positions of the phase boundaries may

be derived, particularly when using a longitudinal

geometry.

Bibliography

Cowley R A, Jensen J 1992 Magnetic structures and interac-

tions in erbium. J. Phys.: Condens. Matter 4 (48), 9673–96

Ellerby M, McEwen K A, Bauer E, Hauser R, Jensen J 2000

Pressure-dependent resistivity and magnetoresistivity of

erbium. Phys. Rev. B 61 (10), 6790–7

Ellerby M, McEwen K A, Jensen J 1998 Magnetoresistance and

magnetization of thulium. Phys. Rev. B 57 (14), 8416–23

Elliott R J, Wedgwood F A 1963 Theory of the resistance of the

rare-earth metals. Proc. Phys. Soc. 81, 846–54

Hessel Andersen N, Gregers-Hansen P E, Holm E, Smith H,

Vogt O 1974 Temperature-dependent spin-disorder resistivity

in a Van-Vleck paramagnet. Phys. Rev. Lett. 32 (23), 1321–4

Hessel Andersen N, Jensen J, Smith H, Spittorf H, Vogt O 1980

Electrical resistivity of the singlet-ground-state system

1c

Sb. Phys. Rev. B 21 (1), 189–202

Jehan D A, McMorrow D F, Simpson J A, Cowley R A,

Swaddling P P, Clausen K A 1994 Collapsing cycloidal

163

Elemental Rare Earths: Magnetic Structure and Resistance, Correlation of

structures in the magnetic phase diagram of erbium. Phys.

Rev. B 50 (5), 3085–91

Jensen J, Mackintosh A R 1991 Rare Earth Magnetism. Claren-

don, Oxford

Mackintosh A R 1962 Magnetic ordering and electronic struc-

ture of rare-earth metals. Phys. Rev. Lett. 9 (3), 90–3

Mackintosh A R 1963 Energy gaps in spin-wave spectra. Phys.

Rev. Lett. 4 (2), 140–2

McMorrow D F, Jehan D A, Cowley R A, Eccleston R S,

McIntyre G J 1992 On the magnetic phase diagram of erbium

in a c-axis magnetic ﬁeld. J. Phys.: Condens. Matter 4 (44),

8599–608

Miwa H 1963 Energy gaps and electrical resistance associated

with screw-type spin arrangements. Prog. Theor. Phys. 29 (4),

477–93

Pippard B 1989 Magnetoresistance in Metals. Cambridge Uni-

versity Press, Cambridge

Stoner E C 1945 The demagnetizing factors for ellipsoids. Phil.

Mag. 36 (263), 803–21

Watson R E, Freeman A J, Dimmock J P 1968 Magnetic or-

dering and electronic properties of the heavy rare-earth met-

als. Phys. Rev. 167 (2), 497–503

Yamada H, Takada S 1973 Magnetoresistance due to electron-

spin scattering in antiferromagnetic metals at low tempera-

tures. Prog. Theor. Phys. 49 (5), 1401–19

M. Ellerby

University College, London, UK

ESR Dosimetry: Use of Rare Earth Ions

The trapped electrons (or holes) that are produced

in thermoluminescence (TL) phosphors owing to

irradiation are thermally released and then recom-

bined with emitting centers, resulting in TL. There-

fore, the trapped electrons (or holes) reﬂecting

an accumulated dose are completely released after

measuring the TL.

The signal intensity of ESR owing to unpaired

electrons produced in irradiated crystals is propor-

tional to the exposure dose. The ESR signal intensity

is hardly affected by the measurement because the

dose reading with ESR does not require heating, es-

sentially different from the case of TL. Thus, the

memory of the irradiation is accurately retained in

the crystal after the dose reading. The dose reading

can be carried out repeatedly so that the signal/noise

ratios are increased. Thus, ESR dosimetry is prefer-

able as a low-dose method to TL dosimetry. Alanine

(Regulla and Defﬁner 1982), sucrose (Nakajima and

Otsuki 1987), and gadolinium ion-doped K

Na(SO

)

(Ohta et al . 1997) are known as ESR dosimetry sen-

sors, of which gadolinium ion-doped K

Na(SO

)

the most sensitive.

ESR and TL properties have been described in

Na(SO

)

doped with rare earth (Ln ¼Y, La, Pr,

Nd, Sm, Eu, Gd, Tm, Lu) ions after x-ray irradiation.

ESR and TL spectra of Ln ion-doped K

Na(SO

)

suggest that these dopants predominately substitute

for sodium ions in the K

Na(SO

)

matrix, and the

formation of SO



radicals is promoted by the cation

vacancy that is produced by the charge compensa-

tion, owing to the presence of the trivalent ion. The



radical is isotropic and thermally stable. The

absorption dependence on the ESR signal intensity

of the SO



radical indicates that the ESR signal in-

tensity is proportional to the absorbed dose of x rays

from 10

4

Gy to 10

Gy in yttrium ion-doped

Na(SO

)

and from 10

5

Gy to 10

Gy in gadolin-

ium ion-doped K

Na(SO

)

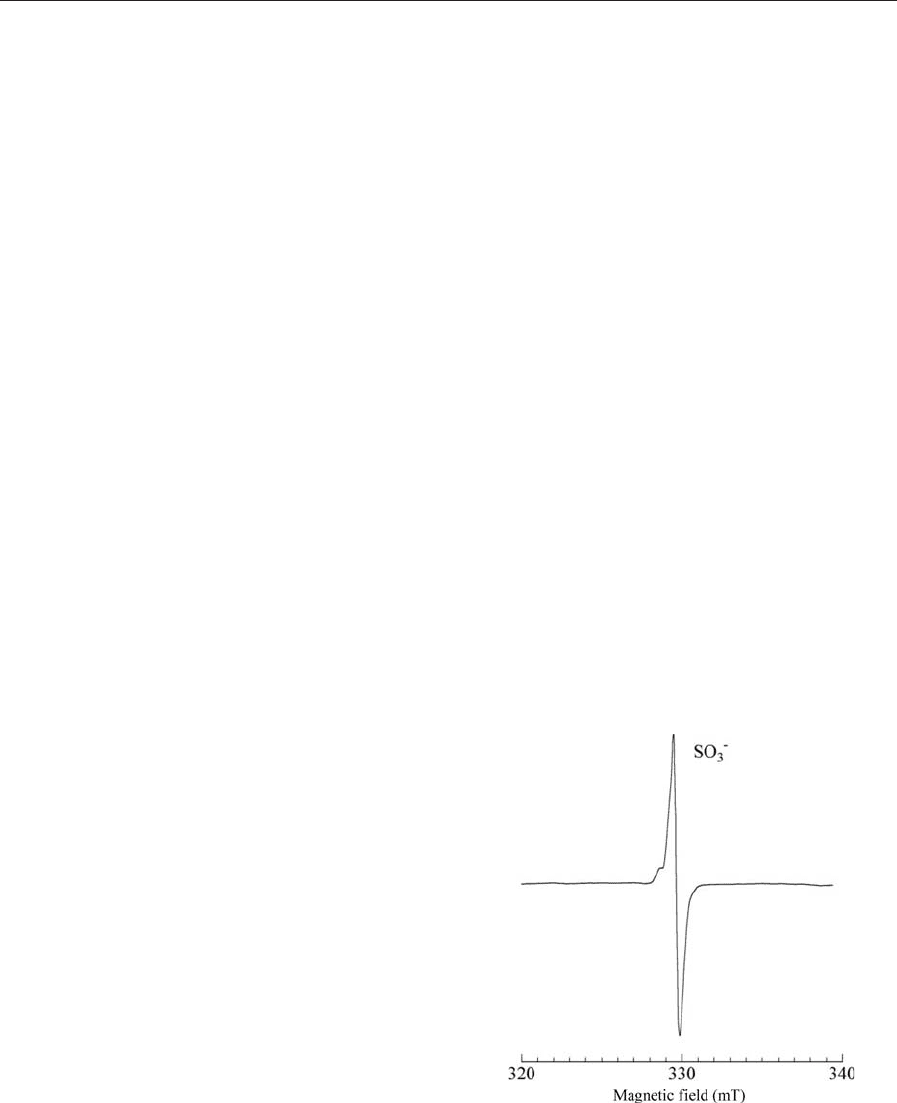
1. ESR Spectra

The typical ESR spectrum of Ln ion-doped K

(SO

)

after x-ray irradiation of about 70 Gy (Fig. 1)

consists of a signal at g ¼2.003, assigned probably to

isotropic SO



radicals (Gromov and Morton 1966,

Luthra and Gupta 1974). This SO



radical is ther-

mally stable up to about 450 K. Furthermore, the

fading of this radical at room temperature is less than

1% yr

1

(Ohta et al. 1992a).

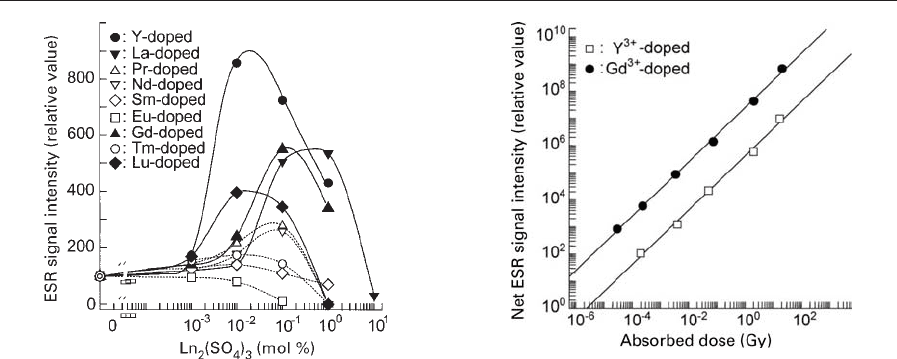
Figure 2 shows the effect of an amount of blended

(SO

)

on the ESR signal intensity. The ESR

signal intensity of SO



radical in stable trivalent

yttrium, lanthanum, gadolinium, or lutetium ion-

doped K

Na(SO

)

is higher than that in praseodym-

ium, neodymium, or thulium ion-doped K

Na(SO

)

and much lower than that in samarium or europium

ion-doped K

Na(SO

)

(Ohta et al. 1997).

Figure 1

Typical ESR spectrum of Ln ion-doped K

Na(SO

)

without ﬁeld gradient after x-ray irradiation of about

70 Gy (after Ohta et al. 1997).

164

ESR Dosimetry: Use of Rare Earth Ions

2. TL Spectra

TL spectra have been measured in order to investi-

gate the valence of the Ln ion-doped K

Na(SO

)

matrix. The TL spectrum of yttrium, lanthanum, or

lutetium ion-doped K

Na(SO

)

consists of a broad,

weak peak (about 400 nm) owing to the K

Na(SO

)

matrix. In praseodymium, neodymium, gadolinium,

or thulium ion-doped K

Na(SO

)

, the TL spectrum

consists of peaks assigned to the f–f transitions of

each Ln

3 þ

ion, i.e., the

transition of Pr

3 þ

the

5/2

13/2

and

5/2

9/2

transitions of

3 þ

, the

7/2

S transition of Gd

3 þ

, and the

, and

transitions of Tm

3 þ

. The TL intensity of

the f–f transition peaks varies according to the fol-

lowing sequence: Gd

3 þ

5Pr

3 þ

,Nd

3 þ

oTm

3 þ

. This

is in contrast to the ESR signal intensity (Fig. 2).

The TL spectrum of samarium ion-doped K

(SO

)

is affected by the glow peak temperature,

i.e., a broad peak owing to the 4f

5d-4f

transition

of Sm

2 þ

and three sharp peaks owing to the

5/2

7/2

, and

5/2

9/2

transitions of

3 þ

are observed near 380 K and near 430 K, res-

pectively. The TL spectrum of europium ion-doped

Na(SO

)

consists of a broad, strong peak owing

to the 4f

5d-4f

transition of Eu

2 þ

3. Formation Mechanism of SO



Radicals

The formation mechanism of SO



radicals can be

interpreted on the basis of the ESR and TL charac-

teristics (Ohta et al. 1992b, 1997). Ln ion-doped

Na(SO

)

after x-ray irradiation reveals that the

higher the ESR signal intensity, the lower the TL

intensity. Since Ln substitutes mainly for potas-

sium or sodium in Ln ion-doped K

Na(SO

)

cation vacancies are created. Consequently, the

2

ion located in the neighborhood of the cation

vacancy can easily capture the free hole released by x-

ray irradiation, resulting in an SO



radical. Most of

the unstable SO



radicals change immediately into



radicals, and some revert to SO

2

ions with TL

emission owing to the electron–hole recombination.

The highest ESR signal intensity probably corre-

sponds to a smaller distortion in the K

Na(SO

)

matrix when it is doped with yttrium or gadolinium,

because the ionic radii of yttrium and gadolinium are

close to that of sodium.

4. Application of SO



Radicals to ESR

Dosimetry

Figure 3 shows the ESR signal intensity of SO



rad-

ical dependence on the absorption dose in yttrium

and gadolinium ion-doped K

Na(SO

)

. The net ESR

signal intensity, which eliminates the intensity before

x-ray irradiation, depends on the absorbed dose of

x rays from 10

4

Gy to 10

Gy in yttrium ion-doped

Na(SO

)

and from 10

5

Gy to 10

Gy in gadolin-

ium ion-doped K

Na(SO

)

(Ohta et al. 1997).

Bibliography

Gromov V V, Morton J R 1966 Paramagnetic centers in irra-

diated potassium sulfate. Can. J. Chem. 44, 527–8

Hayakawa T, Ohta M 1999 Role of dopant on the formation of



radical induced by x-ray irradiation in radical forms in

Na(SO

)

crystals. J. Lumin. 81, 313–9

Luthra J M, Gupta 1974 Mechanism of thermoluminescence in

Sm- and Eu-doped barium sulfate. J. Lumin. 9, 94–103

Figure 2

Effect of amount of blended Ln

(SO

)

on ESR signal

intensity after x-ray irradiation (after Ohta et al. 1997).

Figure 3

ESR signal intensity dependence on x-ray absorbed dose

(after Ohta et al. 1997).

165

ESR Dosi metry: Use of Rare Earth Ions

Nakajima T, Otsuki T 1987 Development of sucrose radiation

dosimeter with free radical. Ouyo Butsuri (Japan) 57, 277–80

Ohta M, Hayakawa T, Furukawa H 1997 Application of lan-

thanide ion doped alkaline metal sulfates to ESR imaging. J.

Alloys Compds. 250, 431–4

Ohta M, Kuroi S, Sakaguchi M 1992a ESR study of x-ray

irradiated rare earth (Ln) ion-doped glaserite and Ln ion-

doped langbeinite. Radioisotopes. 41, 302–7

Ohta M, Sakaguchi M, Sato M 1992b ESR and luminescence

characteristics of glaserite and langbeinite crystals doped

with rare earth ion. Denki Kagaku (Japan) 60, 881–6

Regulla D F, Defﬁner U 1982 Dosimetry by ESR spectroscopy

of alanine. Int. J. Appl. Radiat. Isot. 33, 1101–14

M. Ohta

Niigata University, Niigata City, Japan

166

ESR Dosimetry: Use of Rare Earth Ions

Faraday and Kerr Rotation:

Phenomenological Theory

In 1845 Michael Faraday carried out a series of ex-

periments to determine whether linearly polarized

light, when passed though a transparent insulator,

was inﬂuenced by strong electric ﬁelds. Despite

Faraday’s renowned experimental skills, he failed to

observe any effects. Frustrated, he turned instead to

the use of magnetic ﬁelds. After some initial failures,

on the 13th of September he was able to detect a

small, though dubious, change when using a poor-

quality lead borate glass (Thomas 1991). Fortunately,

some 20 years earlier, between 1825 and 1831, Fara-

day had carried out extensive research into the pro-

duction of optical-grade glass. Although at the time

Faraday considered his research into glasses tedious,

his efforts were now to be handsomely repaid. Using

one of his own optical-quality glasses he had a suf-

ﬁciently perfect medium to demonstrate clearly the

effect that bears his name to this day. The Faraday

effect as it is known, demonstrates that the polariza-

tion state of electromagnetic radiation may be

changed by its passage through an insulating medi-

um when there is a strong magnetic ﬁeld present

(Faraday 1845).

Amazingly, 30 years later in 1875, John Kerr, a

close collaborator of William Thompson (later Lord

Kelvin), repeated Faraday’s quest to demonstrate

that electric ﬁelds can inﬂuence the polarization state

of optical radiation as it passes through a transparent

material. It is a tribute to the keen experimental skills

of Kerr that, where Faraday had failed, he was suc-

cessful. Using a variety of materials, including glass

and later a number of liquids, he demonstrated

the electrooptic effect. On the 26th August 1876, at

the annual meeting of the British Association for the

Advancement of Science held in Glasgow, UK, Kerr

announced a further discovery of an effect that has

since become known as the Kerr magnetooptic effect

(Kerr 1877). Using linearly polarized light from a

narrow parafﬁn ﬂame, Kerr showed that a change in

polarization state occurred on reﬂection from a pol-

ished, soft iron pole-piece of a strong electromagnet.

Given that the changes produced by this effect are

usually very small and are difﬁcult to observe, even

with modern laser sources, the achievement of Kerr

was spectacular. In announcing his discovery Kerr

acknowledged the dependence of his success on the

earlier work of Faraday and later Verdet, who in

1854 had demonstrated the Faraday effect in semi-

transparent paramagnetic media (Verdet 1854).

The Kerr and the Faraday effects are now collec-

tively known as magnetooptical effects and their mi-

croscopic origins are well understood (Freiser 1968).

This article is a phenomenological description of the

various categories of magnetooptic effects as they

may be observed in the laboratory for magnetized

media. For obvious historical reasons magneto-

optical effects that are observed in transmission are

known as Faraday effects. Conversely, effects ob-

served in reﬂection are referred to as Kerr effects.

Often, there is some confusion in referring to the Kerr

effect in reﬂection from materials that are not opti-

cally opaque and where radiation may have traveled

through the material and back again several times,

eventually appearing on the side of reﬂection as a

multiply reﬂected beam. However, it is convention to

refer to effects observed in the reﬂected ﬁeld as Kerr

effects and in transmission as Faraday effects.

In describing magnetooptical effects it is convenient

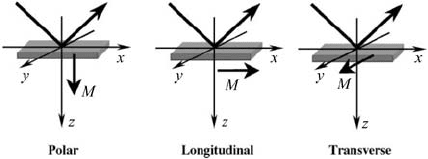
to categorize them into three principal conﬁgurations

deﬁned by the orientation of the magnetization

vector (M) relative to the plane of the reﬂecting sur-

face and to the plane of incidence of the incident

radiation. The three conﬁgurations are referred to as

the polar, longitudinal, and transverse orientations

(Fig. 1).

1. Polar and Longitudinal Effects

In the polar and longitudinal cases, effects occur for

incident radiation polarized either in the P-plane

(electric vector parallel to the plane of incidence) or

the S-plane (electric vector perpendicular to the plane

of incidence). Radiation incident in either of these

linearly polarized states is, on reﬂection, converted to

elliptically polarized light. The major axis of the el-

lipse is often rotated slightly with respect to the prin-

cipal plane and this is commonly referred to as the

Kerr rotation. There is also an associated ellipticity

and this is called the Kerr ellipticity. At the same

time, similar effects occur in transmission, in this case

producing Faraday rotation and ellipticity. To ﬁrst

order, the size of these effects is directly proportional

to the magnitude of the magnetization vector, M.

Furthermore the sense of rotation and ellipticity is

reversed if the magnetization direction is changed by

Figure 1

The three principal magnetooptical conﬁgurations.

167

1801. In each case the magnitudes of the effects vary

with angle of incidence. For the longitudinal case the

effect is zero at normal incidence, which is not true

for the polar conﬁguration.

It is useful to look at these effects in a little more

detail by considering the electric ﬁeld (E) vectors as-

sociated with incident and reﬂected ﬁelds. It should

be noted that it is the interaction between E and M

(indirectly through spin–orbit coupling) that gives

rise to the observed magnetooptical effects. The mag-

netic component of the wave plays no part at optical

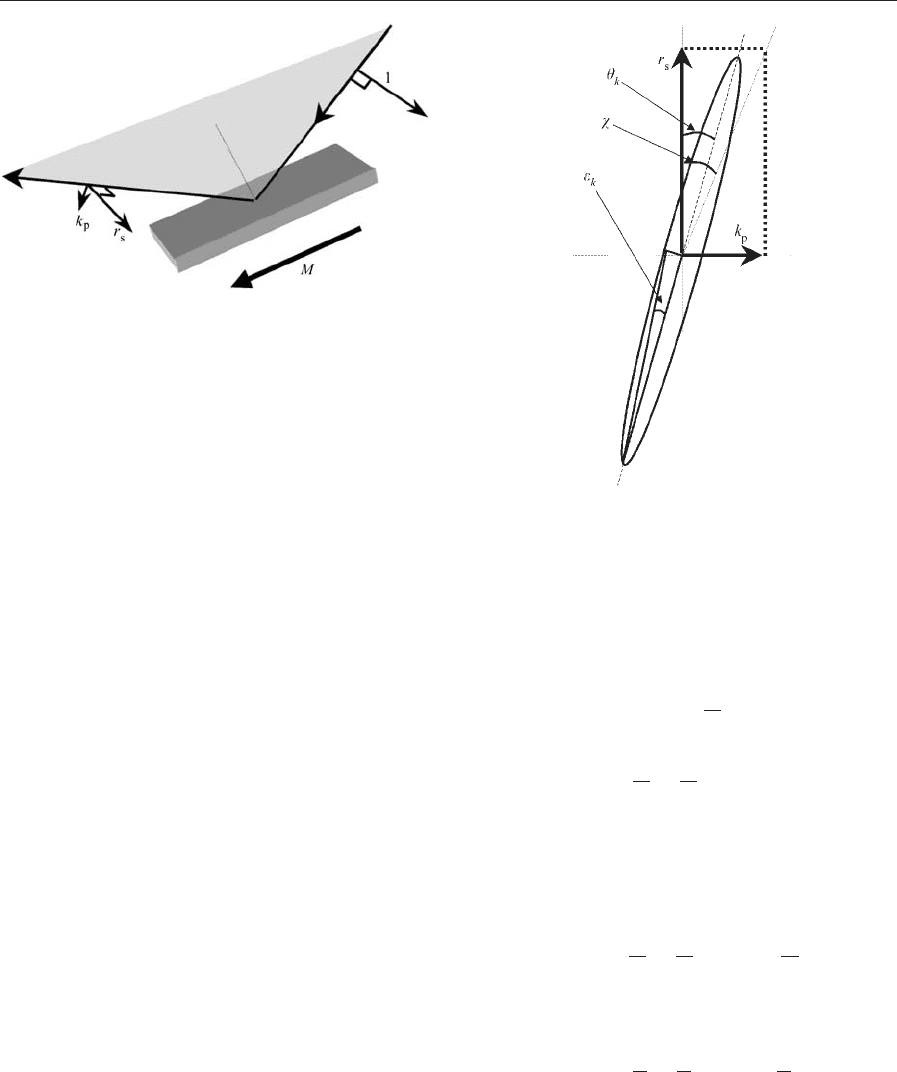
frequencies. As an example, Fig. 2 shows the longi-

tudinal conﬁguration although the discussion also

applies to the polar case. One can see the specific case

of the E vector incident in the S-plane. If the incident

ﬁeld amplitude is taken as unity, the reﬂected beam

will consist of two orthogonal complex vectors. One

is the usual Fresnel amplitude reﬂection coefﬁcient,

, while the other is a small component, k

, called the

Kerr coefﬁcient. The subscripts p and s refer to the

directions parallel and perpendicular to the plane of

incidence, respectively. In general, these two vectors

represent the amplitudes of oscillating electromag-

netic ﬁelds and may be out of phase with each other.

Together they give rise to elliptically polarized light

as illustrated in Fig. 3, where the observer is looking

along the reﬂected beam towards the sample surface.

In this case the Kerr rotation, y

, is in a clockwise

direction and is counted as positive. Likewise, if the

locus of the resultant E vector rotates in a clockwise

direction in time, as indicated in Fig. 3 the ellipticity,

, is positive. In a similar way, the transmitted beam

may also become elliptically polarized with amplitude

transmission coefﬁcient t

and Faraday coefﬁcient f

leading to a rotation y

and ellipticity e

In general, and with reference to Fig. 3, the Kerr

rotation and ellipticity are given by the following

ellipsometric expressions:

tan 2y

¼ tan2wcosD

ð1Þ

and

sin 2e

¼ sin2wsinD

ð2Þ

where

tan w ¼



ð3Þ



ð4Þ

and D

is the angular phase difference between the

two orthogonal vectors. In many instances the mag-

netooptical coefﬁcients are very small; consequently,

when 7k

757r

7 a simple complex Kerr rotation,

may be deﬁned as

¼ y

þ ie



cos D

þ i



sin D

ð5Þ

Similarly, if 7f

757t

7 a complex Faraday rotation,

, may be deﬁned as

¼ y

þ ie



cos D

þ i



sin D

ð6Þ

It should be noted that similar expressions apply for

light incident in the P-plane, in which case the

associated coefﬁcients are k

, f

, r

, and t

. In addi-

tion, by reversing the magnetization, the signs of the

Figure 2

Electric ﬁeld amplitudes associated with the longitudinal

Kerr effect.

Figure 3

Elliptically polarized light showing Kerr rotation, y

and ellipticity, e

168

Faraday and Kerr Rotation: Phenomenological Theory

magnetooptical coefﬁcients are changed and so too is

the sense of the complex Kerr rotation.

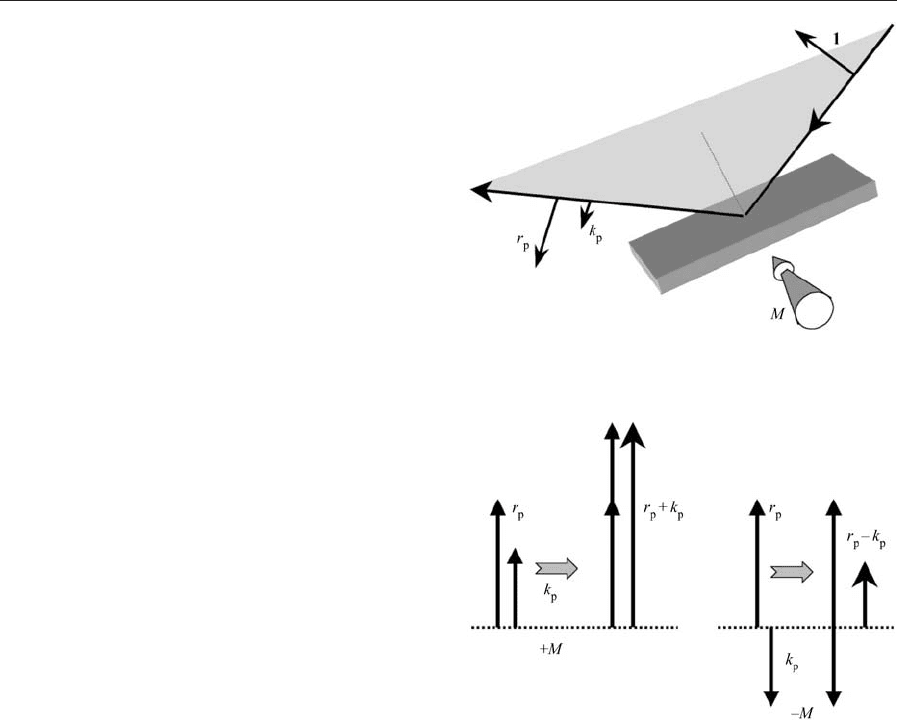
2. Transverse Effect

The transverse situation is quite different from that

described above. First, an effect is only observed for

radiation polarized in the P-plane. Second, the radi-

ation remains linearly polarized after reﬂection, al-

though the reﬂected intensity changes by a small

amount on reversal of the magnetization. This effect

varies with angle of incidence and is zero at normal

incidence. The situation in reﬂection is illustrated in

Fig. 4 where the incident unit amplitude in the P-plane

gives rise to the usual Fresnel amplitude reﬂection co-

efﬁcient, r

,togetherwithasmallKerrcomponent,k

The combination of these two vectors, which are not

necessarily in phase, results in an intensity reﬂectivity

that changes as the magnetization is switched between

the two antiparallel states, 7M.Thisisillustrated

schematically in the amplitude diagram of Fig. 5 where

the resultant amplitudes are shown for the two cases.

Since the measurable intensity reﬂectance is equal to

the square of the modulus of the resultant amplitude

reﬂectance, the two reﬂectances, R

, are given by

¼ 7r

þ k

and R



¼ 7r

 k

ð7Þ

Hence, on magnetization reversal a change, DR,

occurs with a mean intensity reﬂectance, R,where

DR ¼ R

 R



and R ¼ðR

þ R



Þ=2 ð8Þ

3. Permittivity Tensor

As already mentioned, it is the interaction of the

electric ﬁeld vector with the medium that gives rise to

magnetooptical effects and for this reason the intrin-

sic material properties are contained within a skew-

symmetric permittivity tensor, [e]. The form of this

tensor may be determined on symmetry grounds since

a rotation of the Cartesian coordinate system around

the magnetization direction should leave the material

properties unchanged. The tensor, for an otherwise

isotropic medium, is given below for the magnetiza-

tion vector pointing along the positive z-direction:

½e¼e

1 iQ 0

þiQ 10

001

ð9Þ

where e

is the permittivity of free space and n ( ¼n

) is the complex refractive index of the material. Q

( ¼Q

þiQ

) is the magnetooptic parameter that

gives rise to the previously described effects. It should

be noted that the positions of the plus and minus

signs in this tensor depend upon the particular sign

convention chosen to carry out magnetooptical cal-

culations. Moreover the choice of convention has

implications for the sense of the complex magneto-

optical rotations. For this reason it is important

to adopt a clearly deﬁned system. The various op-

tions are described in the literature (Atkinson and

Lissberger 1992) and it should be noted that the self-

consistent preferred scheme described in this refer-

ence is used here.

4. Normal Incidence Polar Case

In magnetooptical recording applications the normal

incidence polar conﬁguration is most commonly used

because the Kerr and Faraday effects are relatively

large and normal incidence is convenient from a

practical point of view. In such situations the mag-

netooptical effects can also be understood from the

Figure 4

Electric ﬁeld amplitudes associated with the transverse

Kerr effect.

Figure 5

Electric ﬁeld amplitudes associated with the transverse

Kerr effect.

169

Faraday and Kerr Rotation: Phenomenological Theory