Burton T. (et. al.) Wind energy Handbook
Подождите немного. Документ загружается.

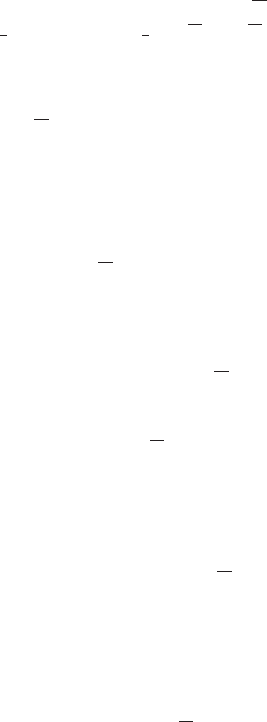
A5.3 Resonant Displacement Response Ignoring Wind
Variations along the Blade
A5.3.1 Linearization of wind loading
For a fluctuating wind speed U(t) ¼ U þ u(t), the wind load per unit length on the
blade is
1
2
C
f
rU
2
(t)c(r) ¼
1
2
C
f
r[U
2
þ 2Uu(t) þ u
2
(t)]c(r), where C
f
is the lift or drag
coefficient, as appropriate, and c(r) is the local blade chord dimension. In order to
permit a linear treatment, the third term in the square brackets, which will normally
be small compared to the first two, is ignored, so that the fluctuating load q(r, t)
becomes C
f
rUu(t)c(r).
A5.3.2 First mode displacement response
Setting q(r, t) ¼ C
f
rUu(t)c(r), the first mode tip displacement response to a sinusoi-
dal wind fluctuation of frequency n (¼ ø=2) and amplitude u
o
(n) given by Equa-
tion (A5.3) becomes
f
1
(t) ¼
ð
R
0
1
(r)C
f
rUc(r)dru
o
(n)jH
1
(n)jcos(2nt þ
1
)
¼ C
f
rU
ð
R
0
1
(r)c(r)dru
o
(n)jH
1
(n)jcos(2nt þ
1
) (A5:5)
Hence power spectrum of first mode tip displacement is
S
1x
(n) ¼ C
f
rU
ð
R
0
1
(r)c(r)dr
"#
2
S
u
(n)jH
1
(n)j
2
(A5:6)
where S
u
(n) is the power spectrum for the along wind turbulence. Thus the
standard deviation of the first mode tip displacement is given by
2
1x
¼ [C
f
rU
ð
R
0
1
(r)c(r)dr]
2
ð
1
0
S
u
(n)jH
1
(n)j
2
dn (A5: 7)
A5.3.3 Background and resonant respons e
Normally the bulk of the turbulent energy in the wind is at frequencies well below
the frequency of the first out-of-plane blade mode. This is illustrated in Figure A5.1,
where a typical power spectrum for wind turbulence is compared with the square,
jH
1
(n)j
2
, of an example frequency response function for a 1 Hz resonant frequency.
The power spectrum is that due to Kaimal (and adopted in Eurocode 1, 1997):
RESONANT DISPLACEMENT RESPONSE IGNORING WIND VARIATIONS 315
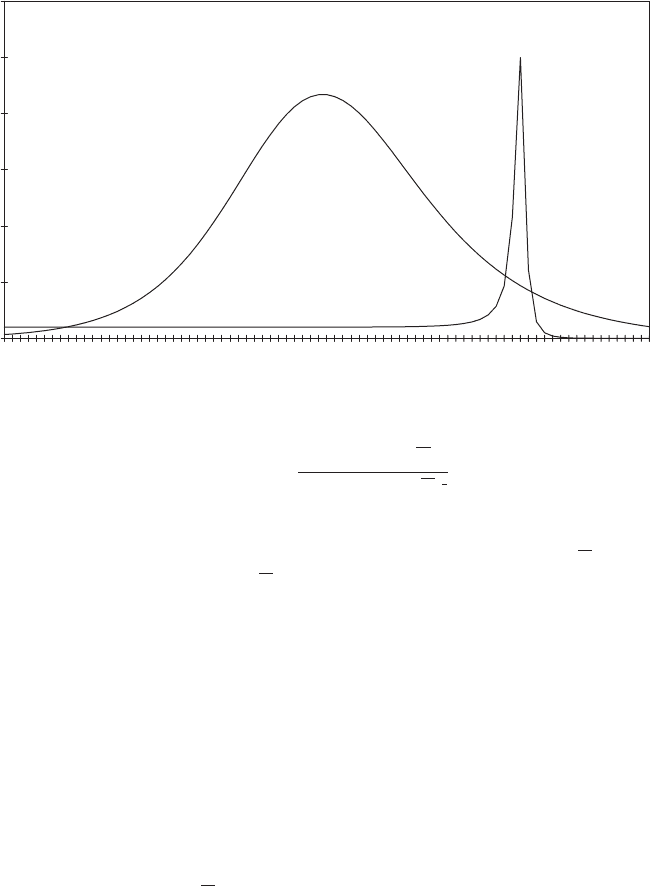
nS
u
(n) ¼
2
u
0:1417nL
x
u
=U
(0:098 þ nL
x
u
=U)
5
3
(A5:8)
and is plotted as the non-dimensional power-spectral density function, R
u
(n) ¼
nS
u
(n)=
2
u
, against a logarithmic frequency scale. The time scale, L
x
u
=U, chosen is
5 s, based on a mean wind speed,
U,of45m=s and an integral length scale, L
x
u
,of
225 m.
In view of the fact that the resonant response usually occurs over a narrow band
of frequencies on the tail of the power spectrum, it is normal to treat it separately
from the quasistatic response at lower frequencies, and to ignore the variation in
nS
u
(n) on either side of the resonant frequency, n
1
(see, for example, Wyatt (1980)).
The variance of total tip displacement then becomes:
2
x
¼
2
B
þ
2
x1
in which the variance of the first mode resonant response,
x1
, is given by
2
x1
¼ C
f
rU
ð
R
0
1
(r)c(r)dr
"#
2
S
u
(n
1
)
ð
1
0
jH
1
(n)j
2
dn (A5:9)
and the re sonant response of higher modes,
2
x2
,
2
x3
etc are ignored. The non-
resonant response,
B
, is termed the background response, and can be derived from
simple static beam theory.
It has been shown by Newland (1984) that
Ð
1
0
jH
1
(n)j
2
dn reduces to
(
2
=2)(n
1
=k
2
1
), where is the logarithmic decrement of damping. The logarithmic
decrement, ,is2 times the damping ratio,
1
, defined as
1
¼ c
1
=2m
1
ø
1
. Hence
Equation (A5.9) becomes
0
0.05
0.1
0.15
0.2
0.25
0.3
0.0001 0.001 0.01 0.1 1 10
Frequency (Hz, logarithmic scale)
Power spectral density,
nSu(n)/su
2
=
0.1417nT/(0.098 +
nT )
5/ 3
with T = 5 s
Square of frequency
response function,
x1/100, for damping ratio
of 0.1 and natural
frequency of 1 Hz
(stiffness, k, taken as
unity)
Figure A5.1 Power Spectrum and Frequency Response Function
316
DESIGN LOADS FOR HORIZONTAL-AXIS WIND TURBINES

2
x1
¼ C
f
rU
ð
R
0
1
(r)c(r)dr
"#
2
S
u
(n
1
)
2
2
n
1
k
2
1
(A5:10)
For comparison, the first mode component,
x
1
, of the steady response is obtained by
setting ø ¼ 0 and q
0
(r) ¼
1
2
rU
2
C
f
c(r) in Equation (A5.3), yielding
x
1
¼
1
2
rU
2
C
f
1
k
1
ð
R
0
1
(r)c(r)dr (A5:11)
Hence the ratio of the standard deviation of the firs t mode resonant response to the
first mode component of the steady response is
x1
x
1
¼ 2
u
U
ffiffiffiffiffiffi
2
p
ffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffi
n
1
S
u
(n
1
)
2
u
s
¼ 2
u
U
ffiffiffiffiffiffi
2
p
ffiffiffiffiffiffiffiffiffiffiffiffiffiffi
R
u
(n
1
)
p
(A5:12)
Note that towards the upper tail of the power spectrum of along wind turbulence,
where n
1
is likely to be located,
ffiffiffiffiffiffiffiffiffiffiffiffiffiffi
R
u
(n
1
)
p
tends to
ffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffi
0:1417=(nL
x
u
=
U
)
p
1
3
.
A5.4 Effect of Across-wind Turbulence Distribution on
Resonant Displacement Response
In the foregoing treatment, the wind was assumed to be perfectly correlated along
the blade. The implications of removing this simplifying assumption will now be
examined.
The fluctuating load on the blade, q(r, t), becomes C
f
rUu(u, r)c(r) per unit length,
and the generalized fluctuating load with respect to the first mode becomes
Q
1
(t) ¼
ð
R
0
1
(r)q(r, t)dr ¼ C
f
rU
ð
R
0
u(r, t)c(r)
1
(r)dr (A5:13)
The standard deviation,
Q
,ofQ(t) is given by
Q1
2
¼
1
T
ð
T
0
Q
2
1
(t)dt ¼ (rUC
f
)
2
1
T
ð
T
0
ð
R
0
u(r, t)c(r)
1
(r)dr
"#
ð
R
0
u(r9, t)c(r9)
1
(r9)dr9
"#
dt
¼ (rUC
f
)
2
ð
R
0
ð
R
0
1
T
ð
T
0
u(r, t)u(r9, t)dt
"#
c(r)c(r9)
1
(r)
1
(r9)dr dr9 (A5:14)
Now the expression within the square brackets is the cross correlatio n function ,
k
u
(r, r9, ) ¼ Efu(r, t)u(r9, t þ )g with set equal to zero. The cross correlation
function is related to the cross spectrum, S
uu
(r, r9, n), as follows:
EFFECT OF ACROSS-WIND TURBULENCE DISTRIBUTION 317

k
u
(r, r9, ) ¼
1
2
ð
1
1
S
uu
(r, r9, n) exp(i2n)dn
giving
k
u
(r, r9,0)¼
1
T
ð
T
0
u(r, t)u(r9, t)dt
"#
¼
ð
1
0
S
uu
(r, r9, n)dn for ¼ 0 (A5:15)
Hence
Q1
2
¼ (rUC
f
)
2
ð
R
0
ð
R
0
ð
1
0
S
uu
(r, r9, n)dn
c(r)c (r9)
1
(r)
1
(r9)dr dr9 (A5:16)
The normalized cross spectrum is defined as S
N
uu
(r, r 9, n) ¼ S
uu
(r, r9, n)=S
u
(n), and
like S
uu
(r, r9, n), is in general a complex quantity, because of phase differences
between the wind speed fluctuations at different heights. As only in-phase wind
speed fluctuations will affect the response, we consider only the real part of the
normalized cross spectrum, known as the normalized co-spectrum, and denoted by
ł
N
uu
(r, r 9, n). Substituting in Equation (A5.16), we obtain:
Q1
2
¼ (rUC
f
)
2
ð
R
0
ð
R
0
ð
1
0
S
u
(n)ł
N
uu
(r, r9, n)dn
c(r)c(r9)
1
(r)
1
(r9)dr dr9 (A5:17)
From this, it can be deduced that the power spectrum of the gene ralized load with
respect to the first mode is
S
Q1
(n) ¼ ( rUC
f
)
2
ð
R
0
ð
R
0
S
u
(n)ł
N
uu
(r, r9, n)c(r)c(r9)
1
(r)
1
(r9)dr dr9 (A5:18)
Note that the power spectrum for the along wind turbulence shows some variation
with height, and so should strictly be written S
u
(n, z) instead of S
u
(n). However,
the variation along the length of a vertical blade is small, and is ignored here.
As for the initial case when wind loadings along the blade were assumed to be
perfectly correlated, the power spectrum for first mode tip displacement is equal to
the product of the power spectrum of the generalized load (with respect to the first
mode) and the square of the frequency response function, i.e.,
S
1x
(n) ¼ S
Q1
(n)jH
1
(n)j
2
(A5:19)
As before, S
Q1
(n) is assumed constant over the narrow band of frequencies
straddling the resonant frequency, and the standard deviation of resonant tip
response becomes:
2
x1
¼ S
Q1
(n
1
)
ð
1
0
jH
1
(n)j
2
dn ¼ S
Q1
(n
1
)
2
2
n
1
k
2
1
(A5:20)
318 DESIGN LOADS FOR HORIZONTAL-AXIS WIND TURBINES
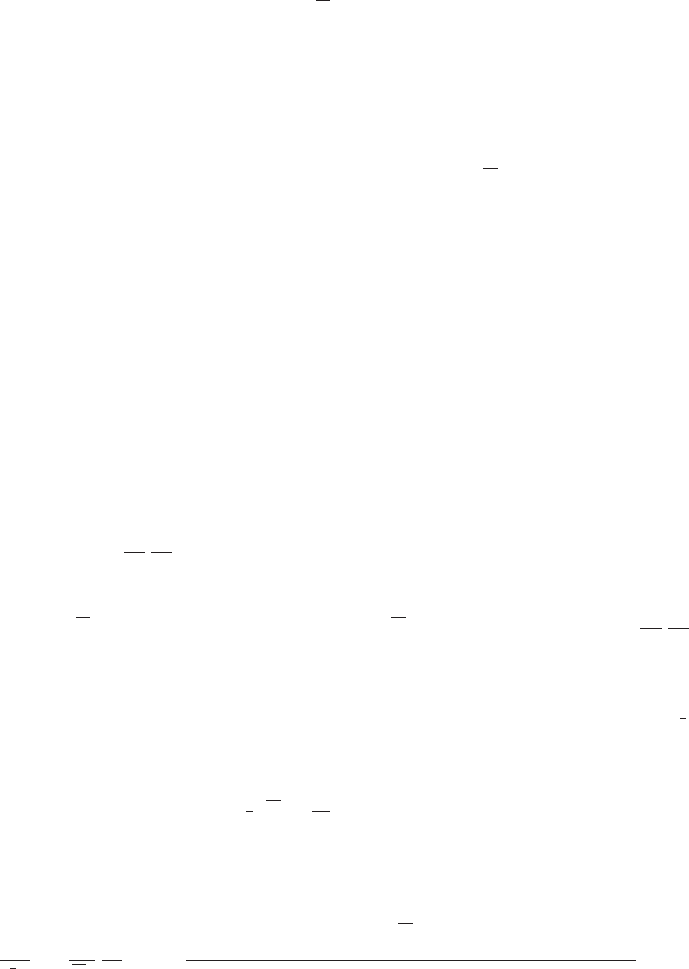
A5.4.1 Formula for normalized co-spectrum
It remains to evaluate S
Q1
(n
1
) ¼ (rUC
f
)
2
S
u
(n
1
)
Ð
R
0
Ð
R
0
ł
N
uu
(r, r9, n) c(r)c(r9)
1
(r)
1
(r9)dr dr9. The normalized co-spectrum, ł
N
uu
(r, r9, n), must decrease as the spacing
[r r9] between the two points consid ered increases, and intuitively it is to be
expected that the decrease would be more rapid for the higher frequency compo-
nents of wind fluctuation. On an empirical basis, Davenport (1962) has proposed an
exponential expression for the normalized co-spectrum as follows:
ł
N
uu
(r, r 9, n) ¼ exp[Cjr r9jn=U] (A5:21)
where C is a non-dimensional decay constant. Davenport noted that measurements
by Cramer (1958) indicated values of C ranging from 7 in unstable conditions to 50
in stable conditions, but recommended the use of the lower figure as being the more
conservative despite the likeliho od of stable condi tions in high winds. Dyrbye and
Hansen (1997) quote Riso measurements reported by Mann (1994) which indicate a
value of C of 9.4, and they recomm end a value of 10 for use in design. A value of 9.2
is implicitly assumed in Eurocode 1 (1997).
There is an obvious inconsistency in the exponential expression for the normal-
ized co-spectrum – when it is integrated up over the plane perpendicular to the
wind direction, the result is positive instead of zero as it should be. This has led to
the development of more complex expressions by Harris (1971) and Krenk (1995).
However, the Davenport formulat ion will be used here, giving
2
x1
¼ S
Q1
(n
1
)
2
2
n
1
k
2
1
¼ (rUC
f
)
2
S
u
(n
1
)
ð
R
0
ð
R
0
exp[Cjr r9jn
1
=U]c(r)c(r9)
1
(r)
1
(r9)dr dr9
2
2
n
1
k
2
1
"#
(A5:22)
The resonant response can be expressed in terms of the first mode component,
x
1
,of
the steady response,
1
2
rU
2
C
f
1
k
1
ð
R
0
1
(r)c(r)dr
from Equation (A5.11) giving
2
x1
x
2
1
¼ 4
2
u
U
2
2
2
R
u
(n
1
)
ð
R
0
ð
R
0
exp [Cjr r9jn
1
=U]c(r)c(r9)
1
(r)
1
(r9)dr dr9
ð
R
0
c(r)
1
(r)dr
!
2
(A5:23)
Hence
EFFECT OF ACROSS-WIND TURBULENCE DISTRIBUTION 319

x1
x
1
¼ 2
u
U
ffiffiffiffiffiffi
2
p
ffiffiffiffiffiffiffiffiffiffiffiffiffiffi
R
u
(n
1
)
p ffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffi
K
Sx
(n
1
)
p
(A5:24)
where
K
Sx
(n
1
) ¼
ð
R
0
ð
R
0
exp [Cjr r9jn
1
=U]c(r)c(r9)
1
(r)
1
(r9)dr dr9
ð
R
0
c(r)
1
(r)dr
!
2
(A5:25)
is denoted the size reduction factor, which results from the lack of correlation of the
wind along the blade. As an example, the size reduction factor, K
Sx
(n
1
), is plotted
out against frequency in Figure A5.2 for the case of a 20 m blade with chord
c(r) ¼ 0:0961R 0: 06467r (Blade TR), assuming a decay constant C of 9.2, and a
mean wind speed
U of 45 m=s. The mode shape taken is the same as for the
example in section 5.6.3 (see Figure 5.3). Also shown for comparison is the
corresponding parameter for a uniform cantilever.
A5.5 Resonant Root Bending Moment
For design purposes it is the augmentation of blade bending moments due to
dynamic effects that is of principal significance. The ratio of the standard deviation
of the first mode resonant root bending moment to the steady root bending moment
(allowing for the lack of correlation of wind fluctuations along the blade) is derived
below.
0
0.1
0.2
0.3
0.4
0.5
0.6
0.7
0.8
0.9
1
0 0.5 1 1.5 2 2.5 3
First mode natural frequency (Hz)
Size redcution factor
Tapered blade ‘TR’
Blade of constant cross section
Figure A5.2 Size Reduction Factors for the First Mode Resonant Response due to Lack of
Correlation of Wind Loading along the Blade-Variation with Frequency for 20 m Blade
320
DESIGN LOADS FOR HORIZONTAL-AXIS WIND TURBINES

Defining M
1
(t) as the fluctuating root bending moment due to wind excitation of
the first mode, we have
M
1
(t) ¼
ð
R
0
m(r)
€
xx
1
(t, r)r dr ¼
ð
R
0
m(r)ø
2
1
x
1
(t, r)r dr ¼ ø
2
1
f
1
(t)
ð
R
0
m(r)
1
(r)r dr
(A5:26)
Hence the standard deviation of M
1
(t),
M1
¼ ø
2
1
x1
ð
R
0
m(r)
1
(r)r dr (A5:27)
The steady roo t bending moment,
M ¼
ð
R
0
1
2
rU
2
C
f
c(r)r dr ¼
1
2
rU
2
C
f
ð
R
0
c(r)r dr (A5:28)
Hence the ratio
M1
M
¼
ø
2
1
x1
ð
R
0
m(r)
1
(r)r dr
1
2
rU
2
C
f
ð
R
0
c(r)r dr
(A5:29)
Substituting the expression for
x1
from Equation (A5.22), we obtain
M1
M
¼
ø
2
1
rUC
f
ffiffiffiffiffiffi
2
p
ffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffi
n
1
S
u
(n
1
)
p
k
1
ð
R
0
m(r)
1
(r)r dr
ffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffi
ð
R
0
ð
R
0
exp[Cjr r9jn
1
=U]c(r)c(r9)
1
(r)
1
(r9)dr dr9
s
1
2
rU
2
C
f
ð
R
0
c(r)r dr
(A5:30)
Noting that R
u
(n) ¼ nS
u
(n)=
2
u
, and that k
1
¼ m
1
ø
2
1
, this simplifies to
M1
M
¼ 2
u
U
ffiffiffiffiffiffi
2
p
ffiffiffiffiffiffiffiffiffiffiffiffi
R
u
(n)
p
ð
R
0
m(r)
1
(r)r dr
m
1
ð
R
0
c(r)r dr
ffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffi
ð
R
0
ð
R
0
exp [Cjr r9j n
1
=U]c(r)c(r9)
1
(r)
1
(r9)dr dr9
s
(A5:31)
RESONANT ROOT BENDING MOMENT 321

where m
1
¼
Ð
R
0
m(r)
2
1
(r)dr is the generalized mass with respect to the first
mode, and the exponential expression within the double integral allows for
the lack of correlation of wind fluctuations along the blade. Substituting
(
Ð
R
0
c(r)
1
(r)dr):
ffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffi
K
Sx
(n
1
)
p
for the square root of the double integral, using Equation
A5.25, leads to
M1
M
¼ 2
u
U
ffiffiffiffiffiffi
2
p
ffiffiffiffiffiffiffiffiffiffiffiffi
R
u
(n)
p
ð
R
0
m(r)
1
(r)r dr
m
1
ð
R
0
c(r)r dr
ð
R
0
c(r)
1
(r)dr
!
:
ffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffi
K
Sx
(n
1
)
p
(A5:32)
Defining the ratio of the integrals,
ð
R
0
m(r)
1
(r)r dr
m
1
ð
R
0
c(r)r dr
ð
R
0
c(r)
1
(r)dr
!
¼
M1
M
x1
x
1
(A5:33)
as º
M1
we obtain
M1
M
¼ 2
u
U
ffiffiffiffiffiffi
2
p
ffiffiffiffiffiffiffiffiffiffiffiffiffiffi
R
u
(n
1
)
p ffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffi
K
Sx
(n
1
)
p
º
M1
(A5:34)
A5.6 Root Bending Moment Background Response
The root bending moment background response can be expressed in terms of the
standard deviation of the root bending moment excluding resonant effects. If the
wind is perfectl y correlated along the blade, this is given by
MB
¼ C
f
rU
u
ð
R
0
c(r)r dr (A5:35)
However, if the lack of correlation of wind fluctuations along the blade is taken into
account,
MB
¼ C
f
rU
u
ffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffi
ð
R
0
ð
R
0
r
u
(r r9)c(r)c(r9)rr9 dr dr9
s
(A5:36)
where r
u
(r r9) is the normalized cross correlation function between simultaneous
wind-speed fluctuations at two different blade radii, and is defined as
r
u
(r r9) ¼
1
2
u
Efu(r, t)u(r9, t þ )g (A5:37)
322 DESIGN LOADS FOR HORIZONTAL-AXIS WIND TURBINES

with set equal to zero. Measurements indicate that the normalized cross correla-
tion function decays exponentially, so it can be expressed as
r
u
(r r9) ¼ exp[jr r9j=L
r
u
] (A5:38)
where L
r
u
is the integral length scale for the longitudinal turbulence component
measured in the across wind direction along the blade, and is thus defined as
Ð
1
0
r
u
(r r)d(r r9). As the integral length scale for longitudinal turbulence meas-
ured vertically in the across wind direction (L
z
u
) is, if anything, less than that
measured horizontally (L
y
u
), it is conservative to treat it as being equal to that
measured horizontally, with the result that L
r
u
can be taken as equal to L
y
u
also.
Typically L
y
u
is approximately equal to 30 percent of L
x
u
, the integral length scale for
longitudinal turbulence measured in the along wind direction. Obse rving that
M ¼
1
2
rU
2
C
f
ð
R
0
c(r)r dr
we can theref ore write
MB
M
¼ 2
u
U
ffiffiffiffiffiffiffiffiffiffiffi
K
SMB
p
(A5:39)
where K
SMB
, the size reduction factor for the root bending moment background
response, is defined as
K
SMB
¼
ð
R
0
ð
R
0
exp[jr r9j=0:3L
x
u
]c(r)c(r9)rr9 dr dr9
ð
R
0
c(r)r dr
!
2
(A5:40)
For a blade with a uniform chord, the integral is straightforward, giving
K
SMB
¼ 4
2
3
1
2
þ
2
4
exp()
2
3
þ
2
4
where ¼
R
0:3L
x
u
(A5:41)
As an example, K
SMB
comes to 0.927 for the case of R ¼ 20 m and L
x
u
¼ 230 m,
indicating that the effect of the lack of correlation of the wind fluctuations is rather
small.
For blades with a normal tapering chord, K
SMB
can be evaluated numerically. In
the case of a blade with a tip chord equal to 25 percent of the maximum chord,
K
SMB
is 0.924 for the same value of as before. It is seen that the taper has a
negligible effect on the end result.
ROOT BENDING MOMENT BACKGROUND RESPONSE 323
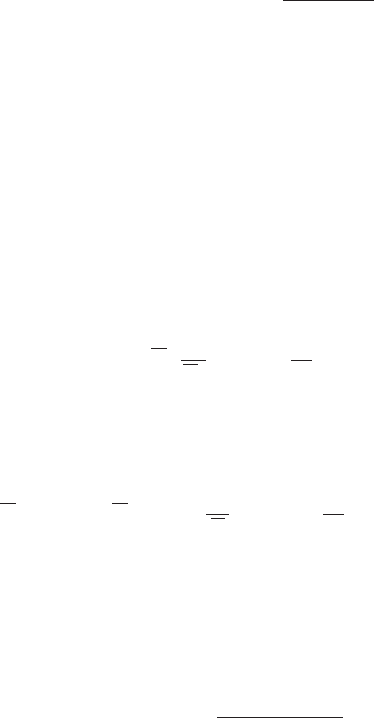
A5.7 Peak Response
One of the key parameters required in blade design is the extreme value of the out-
of-plane bending moment. The 50 year return moment is defined as the expected
maximum moment occurring during the mean wind averaging period wh en the
mean takes the 50 year return value. Treating the moment as a Gaussian process,
Davenport (1964) has shown that the expected value of the maximum departure
from the mean is the standard deviation multiplied by the peak factor, g, where
g ¼
ffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffi
2ln(T)
p
þ
0:5772
ffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffi
2ln(T)
p
(A5:42)
In this formula, is the mean zero-upcrossing frequency of the root moment
fluctuations, and T is the mean wind speed averagi ng period. The variance of the
root bending moment is, in the same way as for the tip displacement, equal to the
sum of the variances of the background and resonant root bending moment
responses, i.e.,
2
M
¼
2
MB
þ
2
M1
(A5:43)
Hence, from Equations (A5.39) and (A5.34), we obtain
2
M
¼
2
MB
þ
2
M1
¼ 4M
2
2
u
U
2
K
SMB
þ
2
2
R
u
(n
1
)K
Sx
(n
1
)º
2
M1
(A5:44)
Thus
M
max
¼ M þ g
M
¼ M 1 þ 2g
u
U
ffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffi
K
SMB
þ
2
2
R
u
(n
1
)K
Sx
(n
1
)º
2
M1
s
0
@
1
A
(A5:45)
The mean zero up-crossing frequency of the root moment fluctuations, , is defined
as
¼
ffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffi
ð
1
0
n
2
S
M
(n)dn
ð
1
0
S
M
(n)dn
v
u
u
u
u
u
t
(A5:46)
where S
M
(n) is the power spectrum of the root moment fluctuations. If we separate
the power spectrum of the background response from the first mode resonant
response at frequency n
1
, then the above expression can be written
324 DESIGN LOADS FOR HORIZONTAL-AXIS WIND TURBINES
