Burton T. (et. al.) Wind energy Handbook

Подождите немного. Документ загружается.

 ¼

ﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃ

(n)dn



þ n



þ 

(A5:47)

Now

(n) ¼ (C

rU)

(n)

(r, r9, n)c(r)c(r9)rr9 dr dr9 (A5:48)

and

M ¼ C

c(r)r dr (A5:49)

(n) ¼ 4

(n)

(r, r9, n)c(r)c(r9)rr9 dr dr9

c(r)r dr

(A5:50)

Deﬁning

SMB

(n) ¼

(r, r9, n)c(r)c(r9)rr9 dr dr9

c(r)r dr

(A5:51)

we obtain

(n) ¼ 4

(n)K

SMB

(n) (A5:52)

Substituting into Equation (A5.47) gives

 ¼

ﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃ

(n)K

SMB

(n)dn



þ n



þ 

(A5:53)

Noting from Equation (A5.52) that 

¼ (4M

)

(n)K

SMB

(n)dn, the ex-

pression for  becomes

PEAK RESPONSE 325

 ¼

ﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃ



þ n



þ 

(A5:54)

where

(n)K

SMB

(n)dn

(n)K

SMB

(n)dn

(A5:55)

Substituting ł

(r, r9, n) ¼ exp[C(r  r9)n=U] into the expression for K

SMB

(n)in

the numerator of Equation (A5.55) gives

(n)K

SMB

(n)dn ¼

(n)

exp[C(r  r9)n=U]c(r)c(r9)rr9 dr dr9

c(r)r dr

(A5:56)

For high frequencies, the double in tegral is, in the limit, inversely proportional to

frequency, so the integrand n

(n)K

SMB

(n) is proportional to n

5=3

1

¼ n

2=3

and the integral does not converge. Consequently it is necessary to take account of

the chordwise lack of correlation of wind ﬂuctuation at high frequencies and, if this

is done, it is found that, in the limit, the integrand is proportional to n

5=3

for which

the integral is ﬁnite. The evaluation of the integral

(n)K

SMB

(n)dn taking

chordwise lack of correlation into account is a formidable task, so the use of an

approximate formula for the frequency, n

, is preferable, especially as the inﬂuence

of n

on the peak factor, g, is slight. One formula is given in Eurocode 1 (1997), but

a simpler one due to Dyrbye and Hansen (1997) for a uniform cantilever is as

follows:

¼ 0:3

ﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃ

ﬃﬃﬃﬃﬃﬃ

(A5:57)

Here R is the blade tip radius and c is the blade chord, assumed constant. For a

tapering chord, the mean chord,

c, can be substi tuted.

A5.8 Bending Moments at Intermediate Blade Positions

A5.8.1 Background response

Denoting the standard deviation of the quasistatic or background bending moment

ﬂuctuations at radius r



as 



), it is apparent that

326 DESIGN LOADS FOR HORIZONTAL-AXIS WIND TURBINES





)



(0)

ﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃ

SMB



)

SMB

(0)



c(r)[r  r



]dr

c(r)r dr

(A5:58)

The ratio of the steady moment at radius r



to that at the root is



c(r)[r  r



]dr=

c(r)r dr, so the ratio of the standard deviation of the quasistatic

ﬂuctuations at radius r



to the steady value there is





)

M(r



)





)



(0)



(0)

M(0)

M(r



)



(0)

M(0)

ﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃ

SMB



)

SMB

(0)

(A5:59)

Generally, the square root will be close to unity, so 



)=M(r



) will be nearly

constant.

A5.8.2 Resonant response

In Section A5.5 it was shown that the standard deviation of the ﬁrst mod e resonant

root bending moment is equal to ø



m(r)

(r)r dr (Equation A5.27). The

corresponding quantity at other radii can be derived similarly, giving





) ¼ ø





m(r)

(r)[r  r



]dr (A5:60)

Hence the ratio of the standard deviation of the ﬁrst mode resonant root bending

moment at radius r



to the steady value there is





)

M(r



)





)



(0)



(0)

M(0)

M(r



)



m(r)

(r)[r  r



]dr

m(r)

(r)r dr

c(r)r dr



c(r)[r  r



]dr



(0)

M(0)

(A5:61)

References

Cramer, H. E., (1958). ‘Use of power spectra and scales of turbulence in estimating wind

loads.’ Second National Conference on Applied Meteororlogy, Ann Arbor, Michigan, USA.

Davenport, A. G., (1962). ‘The response of slender, line-like structures to a gusty wind.’ Proc.

Inst. Civ. Eng., 23, 389–408.

Davenport, A. G., (1964). ‘Note on the distribution of the largest value of a random function

with application to gust loading.’ Proc. Inst. Civ. Eng., 28, 187–196.

Dyrbye, C., and Hansen, S. O., (1997). Wind loads on structures. John Wiley and Sons.

REFERENCES 327

Eurocode 1, (1997). Basis of design and actions on structures – Part 2.4: Actions on structures –

Wind actions.

Harris, R. I., (1971). The nature of the wind. Proceedings of the CIRIA Conference, pp 29–55.

Krenk, S., (1995). ‘Wind ﬁeld coherence and dynamic wind forces.’ Symposium on the advances

in Non-linear Stochastic Mechanics. Kluwer, Dordrecht, Germany.

Mann, J., (1994). ‘The spatial structure of neutral atmospheric surface-layer turbulence.’ J.

Ind. Aerodyn., 1, 167–175.

Newland, D. E., (1984). Random vibrations and spectral analysis. Longman, UK.

Wyatt, T. A., (1980). ‘The dynamic behaviour of structures subject to gust loading’. Proceed-

ings of the CIRIA Conference, ‘‘Wind engineering in the eighties’’ pp 6-1-6-22.

328

DESIGN LOADS FOR HORIZONTAL-AXIS WIND TURBINES

Conceptual Design of Horizontal-

Axis Turbines

6.1 Introduction

Within the general category of horizontal axis wind turbines for grid applications

there exists a great variety of possible machine conﬁgurations, power control

strategies and braking systems. This chapter looks at the different areas where

design choices have to be made, and considers the advantages and disadvantages

of the more conventional options in each case. Inevitably there are situations in

which decisions in one area can impact on those in another, and some of these are

noted.

Alongside these discrete design choices there are several fundamental design

parameters, such as rotor diameter, machine rating and rotational speed, which also

have to be established at the start of the design process. Continuous variables such

as these lend themselves to mathematical optimization, as described in the opening

sections of the chapter.

6.2 Rotor Diameter

The issue of what size of turbine produces energy at minimum cost has been

ﬁercely debated for a long time. Protagonists of large machines cite economies of

scale and the increase in wind speed with height in their favour. From the other

camp, the ‘square-cube law’, whereby energy capture increases as the square of the

diameter, whereas rotor mass (and therefore cost) increases as the cube, is advanced

as an argument against.

In reality, both arguments are correct, and there is a trade-off between economies

of scale and a variant of the ‘square-cube law’ which takes into account the wind

shear effect. This trade -off can be examined with the help of simple cost modelling,

which is considered next.

6.2.1 Cost modelling

The sensitivity of the cost of energy to changes in the values of parameters

governing turbine design can be examined with the aid of a model of the way

component costs vary in response. The normal procedure is to start with a baseline

design, for which the costs of the various components are known. In a rigorous

analysis, the chosen parameter is then assigned a different value and a fresh design

developed, leading to revised component weights, based on which new component

costs can be assigned.

In general, the cost of a component will not simply increase pro rata with its mass,

but will contain elements that increase more slowly. An example is the tower

surface protective coating , the cost of which increases approximately as the square

of the tower height, if all dimensions are proportional to this height. If the design

parameter variation considered is only about þ/50 percent, it is usually sufﬁ-

ciently accurate to represent the relationship between component cost and mass as

a linear one with a ﬁxed component:

C(x) ¼ C



m(x)

þ (1  )



(6:1)

where C(x) and m(x) are the cost and mass of the component respectively when the

design parameter takes the value x, and C

and m

are the baseline values;  is the

proportion of the cost that varies with mass, which will obviously differ for differ-

ent baseline machi ne sizes.

The choice of the value of  inevitably requires considerable expertise as regards

the way manufacturing costs vary with scale, which may be limited in the case of

products at the early stage of development. In view of this, the effort of developing

fresh designs for different design parameter values may well not be justiﬁed, so

resort is often made to scaling ratios based on similarity relationships. This

approach is adopted in the investigation of optimum machine size which follows.

6.2.2 Simpliﬁed cost model for machine size optimization—an

illustration

The baseline machine design is taken as a 60 m diameter, 1.5 MW turbine, with the

costs of the various components taken from Fuglsang and Thomsen (1998). These

are given in Tab le 6.1 as a percentage of the total.

Machine desig ns for other diameters are obtained by scaling all dimensions of all

components in the same proportion, except in the case of the gearbox, generator,

grid connection and controller. Rotational speed is kept inversely proportional to

rotor diameter to maintain constant tip speed, and hence constant tip speed ratio at

a given wind speed. As a result, all machine designs reach rated power at the same

wind speed, so that rated power is proportional to diameter squared. Consequently

the low-speed shaft torque increas es as diameter cubed, which is the basis for

assuming the gearbox mass increases as the cube of rotor diameter, even though the

gearbox ratio changes. Hence, if a blanket value of  of 0.9 is adopted for simplicity,

330 CONCEPTUAL DESIGN OF HORIZONTAL-AXIS TURBINES

the cost of all components apart from gen erator, controller and the grid connection,

for a machine of diameter D, is given by:

(D) ¼ 0:8C

(60) 0:9



þ 0:1

(6:2)

where C

(60) is the total cost of the baseline machine.

The rating of the generator and the grid connection is proportional only to the

diameter squared. It is assumed that Equation (6.1) applies to the cost of these

components, but with mass replaced by rating. Thus, if  is taken as 0.9 once more,

the cost of the generator and grid connection are given by:

(D) ¼ 0:158C

(60) 0:9



þ 0:1

(6:3)

The controller cost is assumed to be ﬁxed. Hence the resulting turbine cost as a

function of diameter is:

(D) ¼ C

(60) 0:80:9



þ 0:1

()

þ 0:158 0:9



þ 0:1

()

þ 0:042

¼ C

(60) 0:72



þ 0:1422



þ 0:1378

(6:4)

As the tower height, along with all other dimensions, is assumed to increase in

proportion to rotor diameter, the annual mean wind speed at hub height wi ll

increase wi th rotor diameter because of wind shear. The energy yield should thus

be calculated taking this effect into account. The cost of energy (excluding opera tion

and maintenance costs) can then be calculated in A/kWh/annum by dividing the

turbine cost by the annual energy yield. The variation of energy cost with diameter,

Table 6.1 Component Costs Expressed as a Percentage of Total Machine

Cost for a 1.5 MW, 60 metre diameter Wind Turbine on Land (from Fuglsang

and Thomsen (1998))

Component Cost as a percentage

of total

Component Cost as a percentage

of total

Blades 18.3% Controller 4.2%

Hub 2.5% Tower 17.5%

Main shaft 4.2% Brake system 1.7%

Gearbox 12.5% Foundation 4.2%

Generator 7.5% Assembly 2.1%

Nacelle 10.8% Transport 2.0%

Yaw system 4.2% Grid connection 8.3%

TOTAL 100%

ROTOR DIAMETER 331

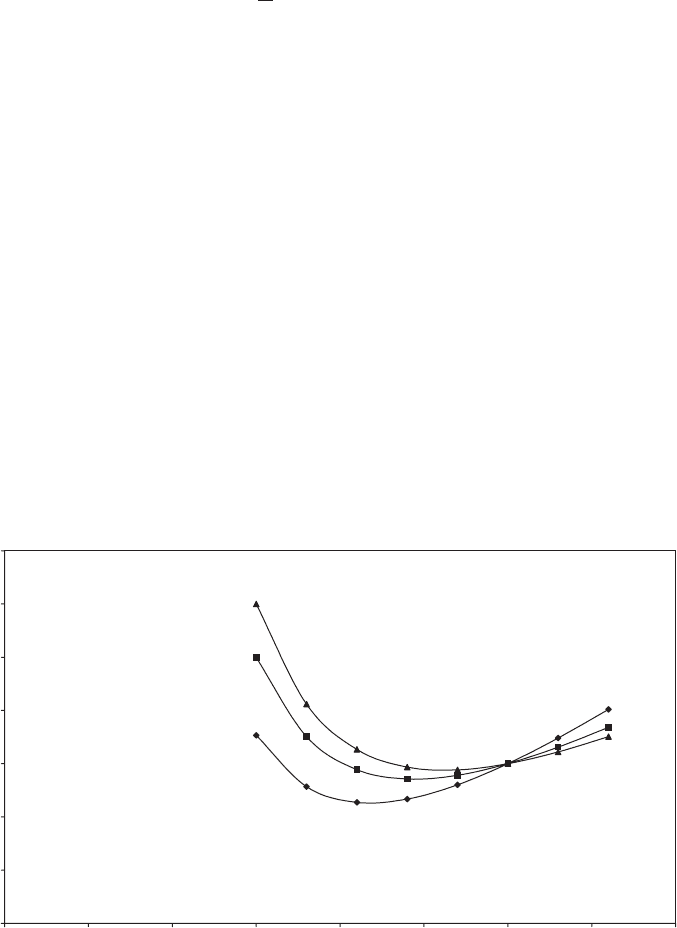
calculated according to the assumptions described above, is plotted in Figure 6.1 for

two levels of wind shear, corresponding to roughness lengths, z

, of 0.001 m and

0.05 m, the hub-height mean wind speed being scaled according to the relation

U(z) / ln(z=z

)(2:10)

(see Section 2.6.2). Also included is a plot for the case of zero wind shear. It is

apparent that the level of wind shear has a noticeable effect on the optimum

machine diameter, which varies from 44 m for zero wind shear to 52 m for the wind

shear corresponding to a surface roughness length of 0.05 m, which is applicable to

farmland with boundary hedges and occasional buildings. Strictly, the im pact of

the increased annual mean wind speed with hub height on the fatigue design of the

rotor and other components should also be taken into account, which would reduce

the optimum mach ine size slightly.

It should be emphasized that the optimum sizes derived abov e depend critically

on the value of  adopted. For example, if  were taken as 0.8 instead of 0.9, the

optimum diameter in the absence of wind shear would increase to 54 m, although

the minimum cost of energy would alter by only 0.3 percent. A more sophisticated

approach would allocate different values of  to different compone nts, as is done in

Fuglsang and Thomsen (1998). Ideally these would be based on cost data on

components of the same design but different sizes.

The co st model outlined above provides a straightforward means of investigating

scale effects on machine economics for a chosen machine design. In practice, the use

of different materials or different machine conﬁgurations may prove more econ-

omic at different machine sizes, and will yield a series of alternative cost versus

diameter curves.

100

110

120

130

140

0 1020304050607080

Rotor diameter (m)

Energy cost index

Zero wind shear

Wind shear corresponding to

= 0.001 m (open sea)

Wind shear corresponding to

= 0.05 m (agricultural land)

Figure 6.1 Variation of Optimum Turbine Size with Wind Shear (Assuming Constant Hub

Height to Diameter Ratio)

332

CONCEPTUAL DESIGN OF HORIZONTAL-AXIS TURBINES

6.3 Machine Rating

The machine rating determines the wind speed (know n as rated wind speed) at

which rated power is reached. If the rating is too high, the rated power will only be

reached rarely, so the cost of the drive train and generator will not be justiﬁed by

the energy yiel d. On the other hand, if the rating is reduced below the optimum

then the cost of the rotor and its supporting structure will be excessive in relation to

energy yield.

The investigation of the optimum relationship between rotor diameter and rated

power can be carried out with the he lp of the cost modelling technique described in

the previous section.

6.3.1 Simpliﬁed cost model for optimizing machine rating in relation

to diameter

Assuming that the blade planform and twist distribution are ﬁxed, the annual

energy yield can be calculated for a number of rated wind speeds, for a given

annual mean wind speed and Weibull shape factor. The turbine rotational speed is

assumed to vary in proportion to the rated wind speed for simplicity. The aim of

the optimization is to obtain the minimum cost of energy, which requires know-

ledge of how the costs of the various turbine components would be affected by the

rating change. Although, in theory, this could only be rigorously derived from

carrying out a series of detailed turbine designs, in practice it is possible to obtain a

useful indication of cost trends by identifying the parameters driving the design of

each component category and investigating their dependence on the rated wind

speed. If the cost split between various components is known for a baseline

machine, these cost trends can then be applied to it in order to determine the

optimum rating. In this case the cost shares given in Table 6.1 for a 60 m diameter,

1.5 MW machine are used once again. The machine is assumed to be pitch regulated.

The parameters determining the design of the majo r components are set out ﬁrst.

(1) Blade weight: the following assumptions are made:

• the blade planform is constant;

• the blade design is governed by out-of-plane bending moments in fatigue;

• the out-of-plane bending moment ﬂuctuations are proportional to the product

of the wind speed ﬂuctuation and the rotational speed (see Equati on (5.25) in

Section 5.7.5);

• the rotational speed is proportional to rated wind speed as already stated;

• the blade skin thickness is proportional to the out-of-plane bending moment

ranges.

Hence the blade skin thickness and therefore the blade weight are propor-

tional to the rated wind speed.

MACHINE RATING 333

(2) Hub weight: it is assumed that this is proportional to the blade out-of-plane

bending moments in fatigue, as in the case of the blade itself.

(3) Low speed shaft weight: this is assumed to be governed by the shaft bending

moment due to the cantilevered rotor and hub weights, which are taken as

proportional to rated wind speed

(4) Gearbox and brake: gearbox and brake design are governed by the rated torque ,

P=Ù. The rated power is pro portional to the cube of the rated wind speed, and

the rotational speed is proportional to the rated wind speed, so the torque

varies as the rated wind speed squared. The weights of the gearbox and brake

are therefore taken to be proportional to the rated speed squared.

(5) Generator: generator design is governed by rated power. The weight of the

generator is therefore assumed to be proportional to the cube of the rated wind

speed.

(6) Nacelle structure and yaw system: it is assumed that the design of these are

governed by the ﬂuctuating moment on the nacelle due to differential blade

out-of-plane root bending moments, which depend on blade out-of-plane

bending moment ﬂuctu ations. The weights are therefore taken to be propor-

tional to rated wind speed.

(7) Tower weight: the tower design may be governed either by fatigue loading

during operation or by extreme loads with the turbine shutdown, so both

possibilities will be considered. In the latter case the tower loading will be

independent of rated wind speed, while in the former it will be mainly

governed by rotor thrust ﬂuctuations, which are assumed to be proportional to

rated wind speed.

(8) Foundation: the foundation design is governed by extreme loads rather than by

fatigue, so it is independent of rated speed.

(9) Grid connection: the weight of cables, switchgear and transformers are assumed

to be proportional to rated power, and hence proportional to rated speed

cubed.

(10) Controller, assembly and transport: these are assumed to be ﬁxed.

The various components listed above are classiﬁed into different categories

according to the way in which their weights vary with rated wind speed in Table

6.2. Also tabula ted are the component costs as a percentage of the total for the

baseline machine, together with the sum for each category.

As noted in Section 6.2.1, the relationship between the cost of a component and

its mass can be approximated by a linear relationship of the form of Equation (6.1).

As before,  is assumed to take a value of 0.9 for all components. When the cost

functions for all the components are added together, the following expression is

334 CONCEPTUAL DESIGN OF HORIZONTAL-AXIS TURBINES