Булатов Н.К., Степановских Е.И. Физическая химия: Опыт решения задач на российских студенческих олимпиадах
Подождите немного. Документ загружается.


31
смешении чистых компонентов 1 и 2, если последние имеют мольные объемы
7,40⋅10
−5
и 9,69⋅10
−5
м
3
/моль.
Решение
1. Для определения v
1
воспользуемся хорошо известными соотношениями:
V
n
c
1
1
= и
V
n
c
2
2
= ,
V = v
1
n
1
+ v
2
n
2
,
21
11
v
сссn
V
+
=== ,
откуда имеем
2
22
1
22
1
v
1
v1v1
v
с
с
с
с
−
−
=
−
=
.
2. Для определения
m
vΔ − изменения мольного объема системы при смеше-
нии чистых компонентов 1 и 2 удобно использовать соотношения:
v = v
1
N
1
+ v
2
N
2
)v(vvvvv
2
o
2
1
o
1
om
NN +−=−=Δ .
c
c
N
k
k
= , v
1
=
c
,
k
k
cN v
=
.
Из них следует, что
⎥
⎦
⎤
⎢
⎣
⎡
−
⎟
⎠
⎞
⎜
⎝
⎛
−−=+−=Δ
2
2
2
o
1
2
o
2
1
o
1
m
v
v
1
v1 v)v(vvv cc
c
c
c
c
o
.
Задача 13
Жидкий тетрахлорметан (вещество k) переводится из начального со-
стояния с температурой
T
o
= 298 К и давлением p
o
=1 атм в конечное с
температурой
T =380 К и давлением p =30 атм. В начальном состоянии
мольный объем ),(v
o
pT
o
o
k
= 9,71⋅10
−5
м
3
/моль, мольная изобарная теплоем-
кость
),(
o
,
pTс
o
o
kp
= 131,7 Дж/(моль⋅К); коэффициент изобарной расширяемо-

32
сти ),(
o
pT
o
o
k
α = 3,08⋅10
−3
К
−1
, коэффициент изотермической сжимаемости
),(
o
pT
o
o
k
β = 9,9⋅10
−10
Па
−1
. Полагая, что мольная изобарная теплоемкость, ко-
эффициенты изобарной расширяемости и изотермической сжимаемости дан-
ного вещества остаются постоянными при этом переходе, вычислить измене-
ние мольной энтропии
o
k
sΔ .
Решение
Изменение любого мольного свойства )( p,Te
o
k
чистого вещества k в
рамках одного и того же агрегатного состояния описывается дифференци-
альным уравнением вида
dp
p
e
dT
T
e
de
T
o
k
p
o
k
o
k
⎟
⎟
⎠
⎞
⎜
⎜
⎝
⎛
∂
∂
+
⎟
⎟
⎠
⎞
⎜
⎜
⎝
⎛
∂
∂
= .
В частности для мольной энтропии имеем
dp
p
s
dT
T
s
ds
T
o
k
p
o
k
o
k
⎟
⎟
⎠
⎞
⎜
⎜
⎝
⎛
∂
∂
+
⎟
⎟
⎠
⎞
⎜
⎜
⎝
⎛
∂
∂
= .
Учитывая, что
T
c
T
s
o
k,p
p
o
k
=
⎟
⎟
⎠
⎞
⎜
⎜
⎝
⎛
∂
∂
, и принимая во внимание дифференциальное
соотношение взаимности
p
o
k
T
o
k
Tp
s
⎟
⎟
⎠
⎞
⎜
⎜
⎝
⎛
∂
∂
−=
⎟
⎟
⎠
⎞
⎜
⎜
⎝
⎛
∂
∂
v
, а также выражение для ко-
эффициента изобарической расширяемости
p
o
k
o
k
o
k
T
⎟
⎟
⎠
⎞
⎜
⎜
⎝
⎛
∂
∂
=α
v
v
1
, получаем
dpdT
T
Tñ
ds
o
k
o
k
o
k,p
o
k
v
)(
α−= .
Интегрирование этого уравнения дает:
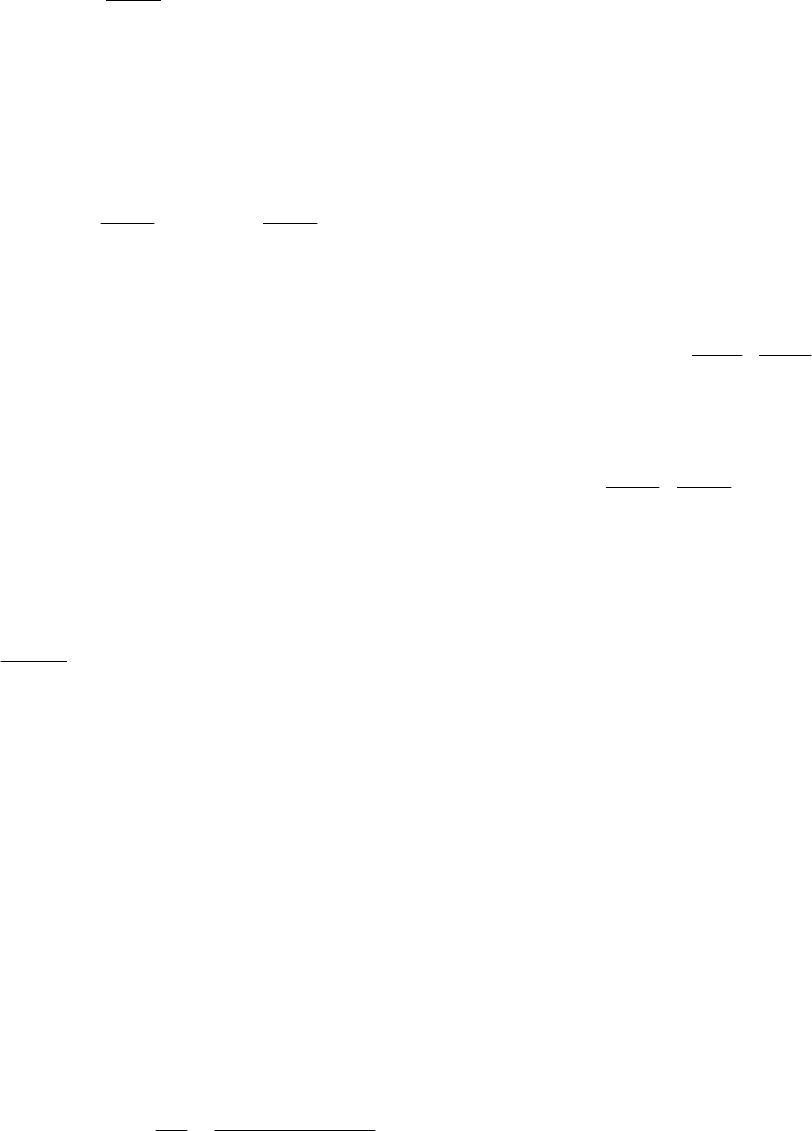
33
dpT,pdT
T
c
s
o
k
p
p
o
k
T
T
o
k,p
o
k
oo
)(v
∫∫
α−=Δ . (12)
Зависимость мольного объема от температуры и давления может быть найде-
на по уравнению
dp
p
dT
T
d
T
o
k
p
o
k
o
k
⎟
⎟
⎠
⎞
⎜
⎜
⎝
⎛
∂
∂
+
⎟
⎟
⎠
⎞
⎜
⎜
⎝
⎛
∂
∂
=
vv
v
,
которое с учетом коэффициента изобарного расширения
p
o
k
o
k
o
k
T
⎟
⎟
⎠
⎞
⎜
⎜
⎝
⎛
∂
∂
=α
v
v
1
и коэффициента изотермической сжимаемости
T
o
k
o
k
o
k
p
⎟
⎟
⎠
⎞
⎜
⎜
⎝
⎛
∂
∂
−=β
v
v
1
преоб-
разуется к виду
dpdT
o
k
o
k
o
k
o
k
β−α=
∂
v
v
или
=
o
k
d vln dpdT
o
k
o
k
β−α
.
Интегрируя это уравнение при условии
o
k
α = const и
o
k
β = const, получаем
[]
.)()(exp vexpvv
o
k
),(
),(
),(
o
o
oo
o
k
pT
o
k
p
p
o
k
T
T
o
k
pT
o
k
pT
o
k
ppTTdpdT
o
oo
o
−β−−α=
⎥
⎥
⎦
⎤
⎢
⎢
⎣
⎡
β−α=
∫∫
Подстановка этого выражения в (12) и интегрирование полученного уравне-
ния при условии
o
kp
с
,
= const приводят к следующему окончательному ре-
зультату:
()
()
[
]
()
[
]
{}
1
v
−−β−−α
β
α
+=Δ
o
o
k
o
o
k
o
k
o
k
oo
o
k
o
o
k,p
o
k
ppexpTTexp
T,p
T
T
lncs
.
Ответ:
o
k
sΔ
= 30,895 Дж/(моль⋅К).

34
Задача 14
Известно, что графит (например, из карандаша) при 298 К и 1 атм са-
мопроизвольно перейти в алмаз не может. Обоснованно ответьте :
1) как влияют давление ( при Т = соnst) и температура (при р = соnst) на
сродство реакции перехода графита в алмаз С
графит
= С
алмаз
;
2) рассчитайте минимальные значения давления (при Т
о
= 298 К) и темпе-
ратуры (при p
о
= 1 атм), при которых значение сродства реакции стано-
вится положительным.
Воспользуйтесь допущением о том, что в случае реакции перехода
графита в алмаз стандартный мольный объем реакции и стандартная мольная
энтропия реакции постоянны, а также приведенными в таблице данными.
Решение
1.
()
,ln,
граф
алм
о
a
a
RTTpAA
rr
−=
но 1
алм
=
a и 1
граф
=
a , поэтому
()
,,
о
TpAA
r
r
= что позволяет записать
=−−=Δ−=
⎟
⎟
⎠
⎞
⎜
⎜
⎝
⎛
∂
∂
=
⎟
⎟
⎠
⎞
⎜
⎜
⎝
⎛
∂
∂
)v(vv
o
граф
o
алм
o
r
T
o
r
T
r
p
A
p
A
−
⎟
⎟
⎟
⎠
⎞
⎜
⎜
⎜
⎝
⎛
ρ
−
ρ
о
граф
о
алм
11
M > 0,
0 )(
o
граф
o
алм
o
<−=Δ=
⎟
⎟
⎠
⎞
⎜
⎜
⎝
⎛
∂
∂
=
⎟
⎠
⎞
⎜
⎝
⎛
∂
∂
sss
T
A
T
A
r
p
o
r
p
r
.
Отсюда ясно, что повышение давления приводит к увеличению срод-
ства
A
r
, тогда как повышение температуры − к уменьшению A
r
.
Значение величин при 298 К и 1 атм Графит Алмаз
Плотность массы,
o
k
ρ , кг/м
3
2250 3510
Стандартная мольная энтропия,
o
k
s , Дж/(моль⋅К)
5,74 2,37
Стандартная мольная энтальпия образования,
o
k
f
hΔ , Дж/моль
0 1830
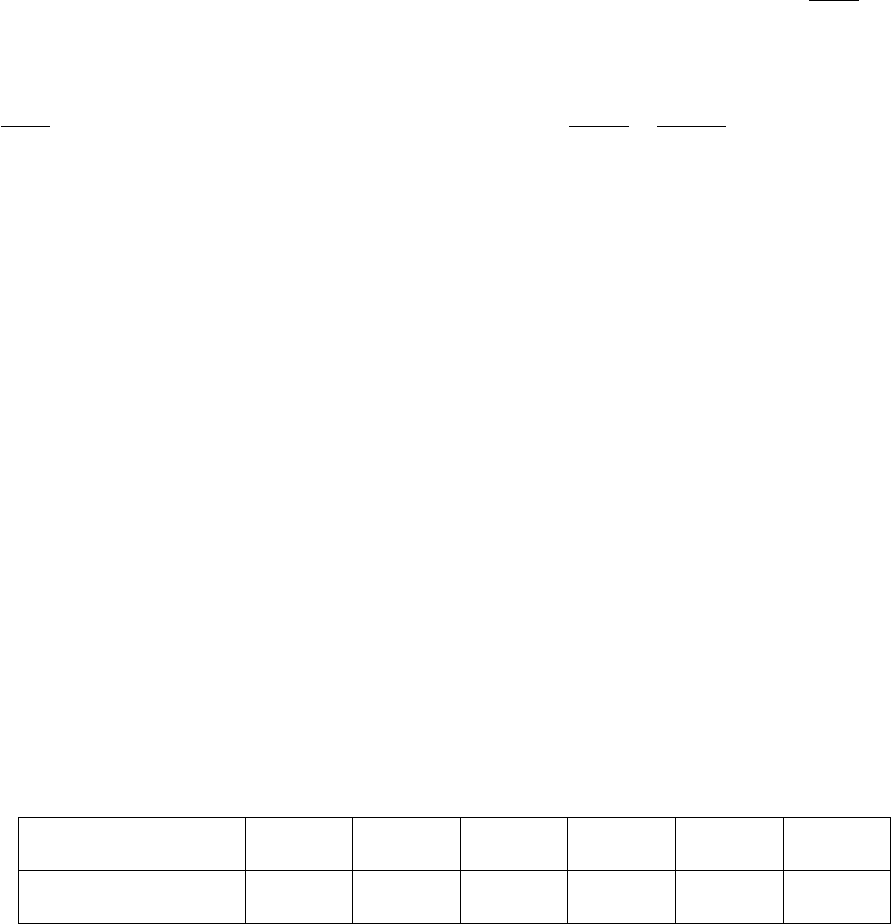
35
2. Найдем сначала
()
oo
r
p,TA :
()()
=Δ+Δ−== )()(
oo
o
r
ooo
o
r
oo
o
r
oo
r
p,TsTp,Thp,TAp,TA
=Δ−Δ+Δ−Δ−= )),(),(()),(),((
графалмграфалм
oo
o
foo
o
fooo
o
foo
o
f
pTspTsTpThpTh
= −2834 Дж/моль.
Отрицательное значение сродства A
r
говорит о том, что при Т
о
и р
о
течение
реакции С
графит
= С
алмаз
возможно лишь справа налево.
Перейдем теперь к поиску р ( при Т
о
= 298 К) и Т ( при р
о
= 1 атм),
удовлетворяющих условиям
(
)
0>p,TA
o
o
r
и
(
)
0>
o
o
r
p,TA соответственно.
Используя приведенные в п.1 выражения для производных
T
o
r
p
A
⎟
⎟
⎠
⎞
⎜
⎜
⎝
⎛
∂
∂
и
p
o
r
T
A
⎟
⎟
⎠
⎞
⎜
⎜
⎝
⎛
∂
∂
, получим
() ( ) ()
o
oo
koo
o
ro
o
r
ppMpTApTA −
⎟
⎟
⎟
⎠
⎞
⎜
⎜
⎜
⎝
⎛
ρ
−
ρ
−=
граф
алм
11
,,;
()( )
(
)
(
)
o
oo
oo
o
ro
o
r
TTsspTApTA −−+=
граф
алм
,,.
Откуда следует, что
()
0>p,TA
o
o
r
, если p >1,5⋅10
4
атм ( при Т=298 К), и
и
()
0>
o
o
r
p,TA , если Т < − 543 K ( при р = 1 атм). Последнее равенство сви-
детельствует, что условие
(
)
0>
o
o
r
p,TA не выполняется никогда при атмо-
сферном давлении
р = 1 атм , так как температура всегда положительная.
Задача 15
Для двухкомпонентного жидкого раствора вода Н
2
О (1-й компонент) −
этанол С
2
Н
6
О (2-й компонент) имеется в табличной форме зависимость
удельной изобарной теплоемкости
с
р,уд
от массы этанола m
2
при постоянной
массе воды
m
1
= 0,5 кг (Т = 298 К, р = 1 атм):
m
2
, кг 0,000 0,050 0,120 0,210 0,330
∞
с
р,уд
, Дж/(К⋅ кг)
4180 4320 4375 4294 4104 2440

36
Требуется: 1) перейти к зависимости изобарной теплоемкости раствора С
р
(Дж/К) от числа молей этанола
n
2
в табличной форме и построить ее график;
2) определить парциальные мольные изобарные теплоемкости обоих компо-
нентов
1,p
c
и
2,p
c
при мольной доле 2-го компонента N
2
= 0,10; 3) вычислить
для тех же компонентов при той же
N
2
парциальные мольные изобарные теп-
лоемкости смешения
m
p
с
1,
Δ и
m
p
с
2,
Δ .
Решение
1. Для построения зависимости изобарной теплоемкости раствора от числа
молей этанола )(
2
nС
p
достаточно использовать следующие формулы:
2
2
2
M
m
n =
;
)(
21уд,
mmcC
pp
+= .
Эта зависимость имеет характер возрас-
тающей функции, ее графический образ
дан на рис. 1.
2. В основе определения
1,p
c и
2,p
c ле-
жит система из двух уравнений вида
22,11,
ncncС
ppp
+
= ,
2,
,,
2
1
p
nTp
p
c
n
C
=
⎟
⎟
⎠
⎞
⎜
⎜
⎝
⎛
∂
∂
.
Найдем сначала по заданной мольной доле
1,0
2
=
N координаты
)( Ap
C
и
)(2 A
n точки А на кривой )(
2
nС
p
:
2
21
,2
1 N
Nn
n
A
−
=
=
)1(
21
21
NM
Nm
−
= 3,087 моль,
)A(p
C = (по графику) Дж/К.
n
2
, моль
p
С , Дж/К
Рис. 1
α
2
A
С
p(A)
n
2(A)

37
Затем определим
2,p
c в точке А графически через тангенс угла наклона каса-
тельной в этой точке: 7,176
22,
=
α
= tgс
p
Дж/(моль⋅К).
Теперь мы имеем возможность вычислить
1,p
c в той же точке А:
1
22,
1,
n
ncC
с
pp
p
−
=
= 81,86 Дж/(моль⋅К).
3. По определению
k
o
kp
kp
o
kp
kp
m
kp
Mcсcсc
,уд,
,
,
,
,
−=−=Δ
.
o
kp
c
уд,,
находим в таблице, приведенной в тексте задачи:
если
2
m = 0, то
о
p
p
cc
1уд,,
уд,
≡
= 4180 Дж/(кг⋅К);
если
2
m = ∞, то
о
p
p
cc
2,уд,
уд,
≡ = 2440 Дж/(кг⋅К);
После подстановки числовых значений получаем:
m
,p
c
1
Δ
= 6,62 Дж/(моль⋅К);
m
,p
c
2
Δ
= 64,46 Дж/(моль⋅К).
Задача 16
Известна зависимость мольной теплоты смешения реального
m
hΔ рас-
твора пропанол (1-й компонент) – бензол (2-й компонент) с мольной долей
бензола
N
2
= 0,45 от температуры Т .
Температура, К 288 298 308 319
m
hΔ , Дж/моль
7790 880 1040 1190
Мольные изобарные теплоемкости чистых компонентов при 298 К равны
o
p
с
1,
= 144,1 Дж/(моль·К),
o
p
с
2,
= 135,4 Дж/(моль·К), а мольная изобарная теп-
лоемкость раствора с
N
2
= 0,45 равна
p
с =153,2 Дж/(моль·К). Определите
двумя способами величину мольной избыточной изобарной теплоемкости
раствора
E
p
c при 298 К.

38
Решение
Разность между мольным экстенсивным свойством e неидеального (ре-
ального) раствора и таким же свойством
èä
e идеального раствора называют
мольной
избыточной функцией реального раствора относительно иде-
ального:
ид
eee
E
−= .
Следовательно, в нашем случае мольная избыточная изобарная тепло-
емкость
=−=
ид
pp
E
p
ccс
2
1,,2
2
,2
1
,1
)()( NcccNcNcc
o
p
o
p
p
o
p
o
p
p
−−=+−
и мольная избыточная энтальпия
−=−= hhhh
E ид
2
12
2
2
1
1
)()( NhhhNhNh
oooo
−−=+
.
Величина
E
h может быть выражена через мольные функции смешения ре-
ального и идеального растворов −
m
hΔ и
ид,m
h
Δ
:
ид,mmE
hhh Δ−Δ= ,
но
ид,m
hΔ = 0 всегда, поэтому
mE
hh Δ= .
Вместе с тем известно, что
{} {}
k
k
Np
m
Np
E
E
p
T
h
T
h
c
,,
⎟
⎟
⎠
⎞
⎜
⎜
⎝
⎛
∂
Δ∂
=
⎟
⎟
⎠
⎞
⎜
⎜
⎝
⎛
∂
∂
=
.
Отсюда появляется возможность определения
E
p
c двумя способами − расчет-
ным и графическим. Первый способ базируется на расчете
E
p
c по известной
p
c при определенной N
2
и известным
o
p
с
1,
и
o
p
с
2,
:
E
p
c =
2
1,2,
)( Nccc
o
p
o
p
p
−− .

39
Второй способ основан на графиче-
ском определении производной
{}
k
Np
m
T
h
,
⎟
⎟
⎠
⎞
⎜
⎜
⎝
⎛
∂
Δ∂
по угловому коэффици-
енту касательной
− тангенсу угла на-
клона касательной tg
α к кривой
)(
Th
m
Δ в точке А с координатой Т(А)
= 298 К (рис. 2).
Задача 17
Для двухкомпонентного жидкого раствора вода Н
2
О (1-й компонент) −
уксусная кислота С
2
Н
4
О
2
(2-й компонент) имеется полученная на опыте в таб-
личной форме зависимость изобарной теплоемкости
С
р
от массовой доли ки-
слоты φ
2
(Т = 298 К, р = 1 атм) при постоянной массе воды m
1
= 0,5 кг:
Требуется: 1) перейти к зависимости изобарной теплоемкости смешения рас-
твора
ΔС
р
m
от числа молей кислоты n
2
в табличной форме и построить ее гра-
фик, имея в виду, что удельные изобарные теплоемкости чистых компонентов
1 и 2 (
o
p
o
p
cc
уд,2,уд,1,
,) равны 4180 и 2056 Дж/(К⋅моль); 2) определить для
обоих компонентов их парциальные мольные изобарные теплоемкости сме-
шения
m
p
c
,1
Δ и
m
p
c
,2
Δ при мольной доле 2-го компонента N
2
= 0,07; 3) вы-
числить для тех же компонентов при той же
N
2
парциальные мольные изо-
барные теплоемкости
,1p
c и
,2p
c .
φ
2
0,057 0,088 0,125 0,161 0,260
С
p
, Дж/К 2238 2314 2398 2476 2682
α
∆h
m
,
Дж/моль
А
Рис. 2
T
,
K

40
Решение
1. Для получения зависимости ΔС
р
m
(n
2
) в табличной и графической фор-
мах необходимо преобразовать табличные данные по зависимости
С
р
(φ
2
) сле-
дующим образом:
)1(
22
21
2
2
2
ϕ−
ϕ
==
M
m
M
m
n
,
=+−=+−=−=Δ )( )(
2
2уд,,
1
1уд,,2,1,
mcmcCCCCCCC
o
p
o
p
p
o
p
o
p
p
o
pp
m
p
)
1
(
2
2
2уд,,1уд,,
1
ϕ−
ϕ
+−=
o
p
o
p
p
ccmC ,
где учтено, что
2
12
2
1 ϕ−
ϕ
=
m
m
.
Графический образ зависимости
ΔС
р
m
(n
2
)
приведен на рис. 3.
m
p
nTp
m
p
c
n
C
tg
2,
,,
2
2
1
Δ=
⎟
⎟
⎠
⎞
⎜
⎜
⎝
⎛
∂
Δ∂
=α
2. В основе определения
m
,p
c
1
Δ и
m
,p
c
2
Δ
лежит система из двух уравнений вида
1
1,
2
2,
ncncС
m
p
m
p
m
p
Δ+Δ=Δ ,
m
p
nTp
m
p
c
n
C
2,
,,
2
1
Δ=
⎟
⎟
⎠
⎞
⎜
⎜
⎝
⎛
∂
Δ∂
.
Сначала следует по заданной мольной доле найти координаты )(
2
An и
m
p
СΔ (А) в точке А на кривой
m
p
СΔ (n
2
) (рис. 3):
2
2
1
1
2
21
1
2
12
11
)(
N
N
M
m
N
Nn
N
N
nАn
−
=
−
==
.
m
p
СΔ (А) = (по графику) Дж/К.
n
2
, моль
m
p
СΔ ,
Д
ж/К
А
Рис. 3
n
2
(
А
)
m
p
СΔ (А)
α
2
