Бухвалов А.В. Финансовые вычисления для профессионалов. Настольная книга финансиста

Подождите немного. Документ загружается.

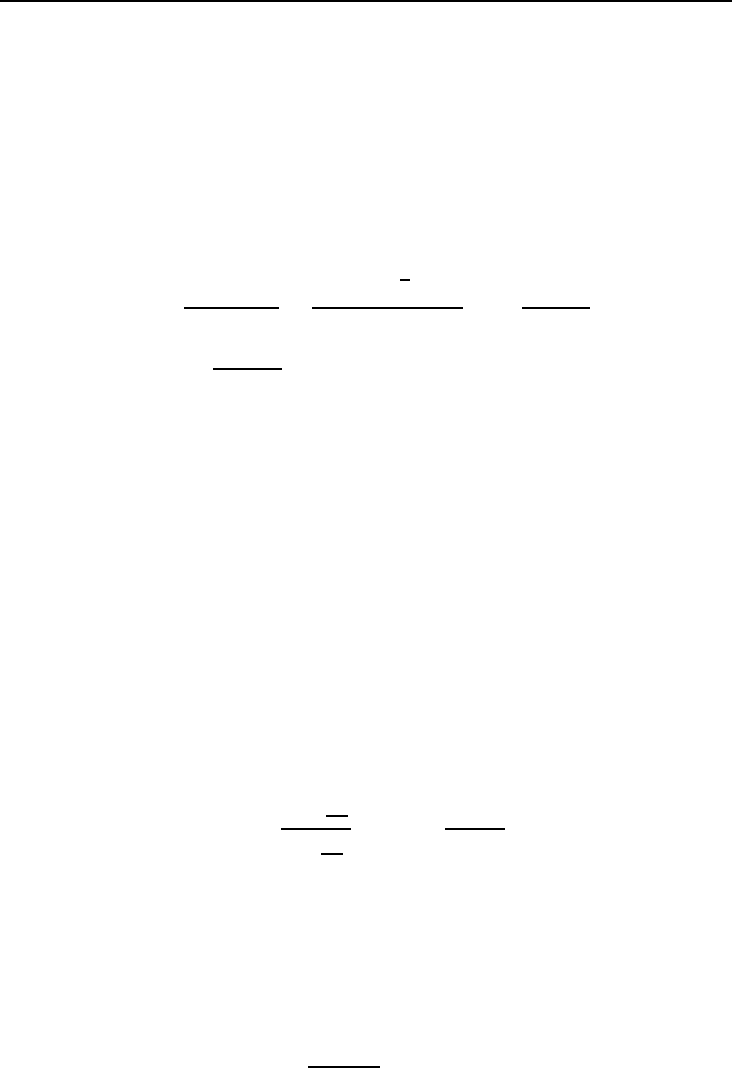
122 6. Финансовые ренты

также как там, после замены множителя (1+i)

на множитель e

δr

найдем

наращенную сумму данной ренты к моменту n:

S = R

+ R

δr

+ R

2δr

+ . . . + R

(n−r)δ

Слагаемые этой суммы являются членами геометрической прогрессии

с первым членом b

= R

, знаменателем q = e

δr

и числом членов k = n/r.

Сумма членов этой прогрессии равна:

S =

− 1)

q − 1



δr

)

− 1



δr

− 1

= R

δn

− 1

δr

− 1

S = R

δn

− 1

δr

−1

. (6.15)

Приведем примеры применения рассмотренных типов рент.

Пример 6.6. Для создания благотворительного фонда ежегодно вы-

деляется по 10 тыс. руб., которые вкладываются в банк, начисляющий

сложные проценты по годовой ставке 12%. Определим сумму, накоплен-

ную в фонде через 6 лет, если: а) взносы в фонд делаются в конце года,

проценты начисляются по кварталам; б) равные взносы делаются в конце

каждого квартала, проценты начисляются по полугодиям; в) взносы дела-

ются в конце каждого года, проценты начисляются непрерывно; г) равные

взносы делаются ежемесячно, проценты начисляются непрерывно.

Решение . а) Взносы образуют годовую ренту с начислением процентов

по ставке j

= 12%. Наращенную сумму вычисляем по формуле (6.9) при

m = 4, n = 6, j

/m = 12%/4 = 3% :

S = R

mn;

= 10 000

24; 3%

4; 3%

По Таблице 2 находим требующиеся значения функции s

n; i

24; 3%

= 34.4265; s

4; 3%

= 4.18363.

Подставив эти значения, получаем:

S = 100 000×

34.4265

4.18363

= 82 288.574 руб.

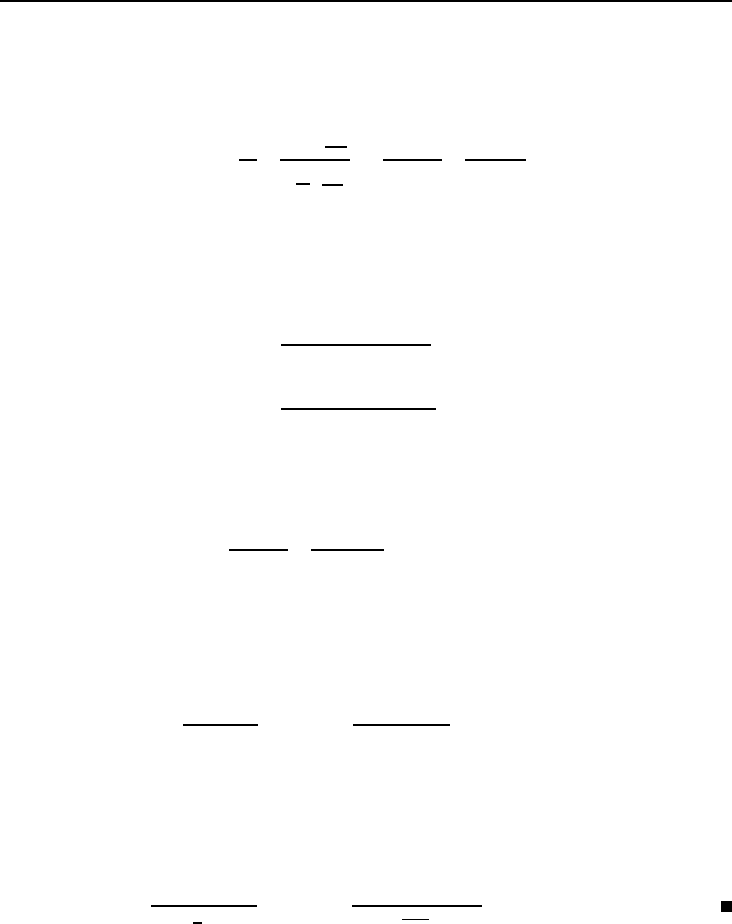
6.4. Виды финансовых рент 123

б) Взносы образуют p -срочную ренту с начислением процентов по

ставке j

= 12%. Наращенную сумму вычисляем по формуле (6.10) при

m = 2, n = 6, p = 4:

S =

mn;

;

10 000

12;6%

0.5;6%

В Таблице 2 нет требуемых значений коэффициента s

n;i

, поэтому вы-

числяем их значения по формуле (6.2):

12; 6%

(1 + 0.06)

− 1

0.06

= 16.8699,

0.5; 6%

(1 + 0.06)

0.5

− 1

0.06

= 0.49271.

Подставляем вычисленные значения и получаем ответ:

S =

10 000

16.8699

0.49271

= 85 597.51 руб.

в) В этом случае взносы образуют годовую ренту с непрерывным на-

числением процентов с силой роста δ = 0.12. Наращенную сумму вычис-

ляем по формуле (6.13) при δ = 0.12, n = 6:

S = R

δn

− 1

− 1)

= 10 000

0.12×6

− 1

0.12

− 1)

= 82 702.69 руб.

г) В этом случае взносы образуют p -срочную ренту с непрерывным

начислением процентов с силой роста δ = 0.12. Наращенную сумму вы-

числяем по формуле (6.14) при δ = 0.12, n = 6, p = 12:

S = R

δn

− 1



− 1



= 10 000

0.12×6

−1



0.12

− 1



= 87 430.82 руб.

Пример 6.7. Какую сумму надо выделять ежегодно для создания бла-

готворительного фонда, чтобы за 6 лет накопить 100 тыс. руб. в каждом

из случаев, описанных в предыдущем примере.

124 6. Финансовые ренты

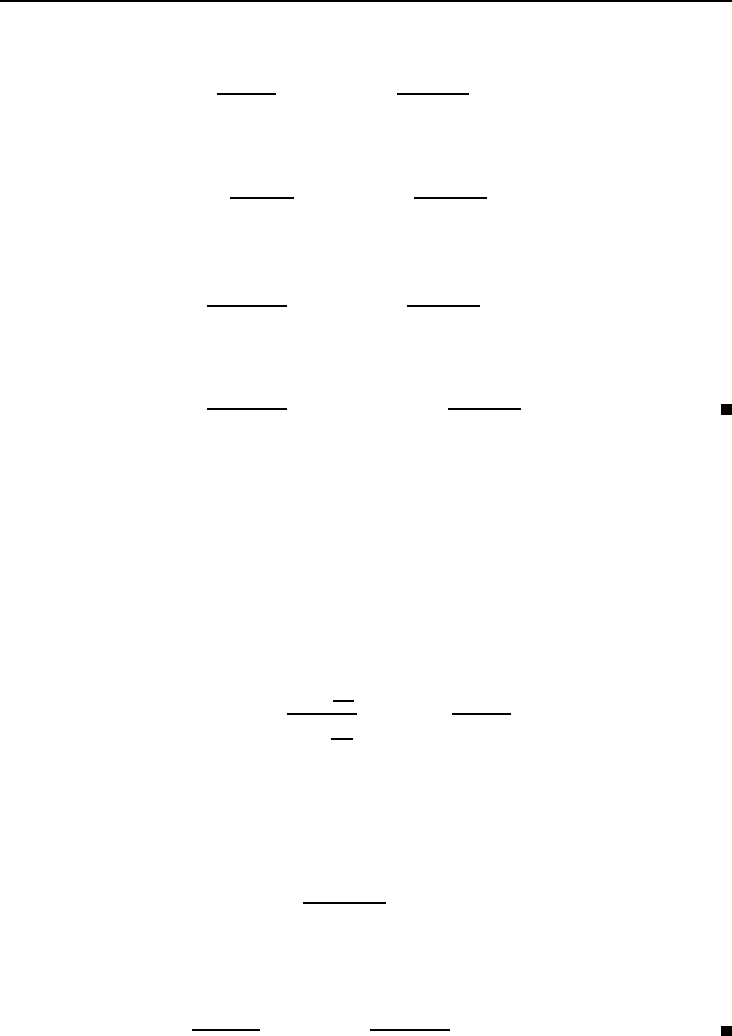
Решение . а) Из формулы (6.9) определяем значение R при S = 100000:

R = 100 000

4; 3%

24; 3%

= 100 000×

4.18361

34.4265

= 12 152.29 руб.

б) Из формулы (6.10) находим R при S = 1 000 000 и p = 4:

R = 100 000×4

0.5; 6%

12; 6%

= 400 000×

0.49272

16.8699

= 11 682.58 руб.

в) Из формулы (6.13) находим R при S = 100 000:

R = 100 000

0.12

− 1

0.72

− 1

= 100 000×

0.12750

1.05443

= 12 091.84 руб.

г) Из формулы (6.14) находим R при S = 100 000 и p = 12:

R = 100 000×12

0.01

− 1

0.72

− 1

= 100 000×12×

0.01005

1.05443

= 11 437.50 руб.

Пример 6.8. Владелец автомастерской кладет в банк в конце каждых

двух лет 10 тыс. руб. Какая су мма будет на счету владельца мастерской

через 10 лет, если: а) на деньги начисляются сложные проценты по ставке

= 12%, б) банк выплачивает непрерывные проценты с силой роста

δ = 12%?

Решение . а) В этом случае наращенную сумму находим по форму-

ле (6.12) при r = 2, m = 4, n = 10, j

/m = 12%/4 = 3%:

S = R

mn;

mr;

= 10 000

40; 3%

8; 3%

По Таблице 2 находим:

40; 3%

= 75.40126, s

8; 3%

= 8.89234.

Подставляем найденные значения и получаем ответ:

S = 10 000×

75.40126

8.89234

= 84 793.54 руб.

б) В этом случае наращенную сумму находим по формуле (6.15) при

δ = 12% = 0.12, n = 10, r = 2:

S = R

δn

−1

δr

− 1

= 10 000×

1.2

− 1

0.24

− 1

= 85 534.53 руб.

6.6. Инвестиции в предприятия 125

6.5. Погашение долгосрочной задолженности

единовременным платежом

Рассмотрим задачу погашения долгосрочной задолженности единовре-

менным платежом.

Должник взял ссуду, равную S руб., которую он должен вернуть через

n лет. Ежегодно он должен выплачивать кредитору проценты по ставке

q. Одновременно он создает погасительный (амортизационный или стра-

ховой) фонд, в который делает ежегодные взносы с целью накопить к мо-

менту возвращения долга необходимую сумму. На деньги, находящиеся в

фонде, должник получает i% в год. Требуется определить так называе-

мую срочную уплату α, то есть суммарные ежегодные затраты должника.

Срочная уплата состоит из выплачиваемых на долг процентов, кото-

рые равны Sq, и взноса в страховой фонд R. Взносы R являются членами

годовой ренты, состоящей из n членов, наращенная сумма которой в мо-

мент n должна быть равна S. По формуле (6.4) R = S/s

n;i

. Срочная

уплата равна:

α = Sq +

n; i

. (6.16)

Пример 6.9. Кредит в 1 млн. руб. получен фирмой в банке под 8%

годовых на 4 года. Одновременно с получением ссуды для ее погашения

создан страховой фонд, в который делаются равные ежегодные взносы.

На деньги, внесенные в фонд, выплачиваются 5% годовых. Найдем еже-

годную срочную уплату по долгу.

Решение . Из Таблицы 2 находим, что

4; 5%

= 4.310125.

По формуле (6.16) при S = 1 000 000, q = 0.08, n = 4, i = 0.05 находим

величину срочной уплаты:

α = 1 000 000×0.08 +

1 000 000

4.310125

= 312 011.83 руб.

При других сроках и условиях выплаты процентов могут быть исполь-

зованы те или иные виды рент, то есть формулы (6.2) – (6.15).

Погашение долгосрочной задолженности несколькими платежами рас-

сматривается в п. 7.4.

126 6. Финансовые ренты

6.6. Инвестиции в предприятия, использующие

невосполняемые ресурсы

Рассмотрим инвестиции в предприятия, использующие невосполняе-

мые ресурсы — таковыми, например, являются предприятия добывающей

промышленности. Капиталовложения делаются с таким расчетом, что-

бы получать в течение срока действия предприятия определенный еже-

годный доход и накопить к моменту истощения ресурсов, используемых

предприятием (запасов ископаемых, например), страховой фонд, равный

сумме инвестиций. Рассмотрим пример.

Пример 6.10. Г-н Макаров хочет купить золотой рудник, который по

прогнозам будет давать в течение следующих 10 лет по 200 000 руб. дохода

в год, после чего окажется полностью исчерпанным. Г-н Макаров хочет

получать 18% ежегодного дохода на вложенную сумму. Одновременно он

собирается установить страховой фонд, чтобы накопить к концу срока

действия рудника вложенную сумму. Сколько он должен заплатить за

рудник, если по вложениям в страховой фонд он может получать 10% в

год?

Решение . Обозначим искомую цену покупки буквой S. Ежегодные вкла-

ды R в страховой фонд образуют ренту, наращенная сумма которой равна

S. По формуле (6.4) имеем:

R =

n; i

10; 10%

Годовой доход от рудника, равный 200 000 руб., состоит из вклада в стра-

ховой фонд и дохода, составляющего 18% от вложенной суммы, то есть

равного 0.18×S руб. Следовательно, сумма S должна удовлетворять урав-

нению:

0.18S +

10; 10%

= 200 000.

По Таблице 2 находим s

10; 10%

= 15.9374. Подставляем это значение в

уравнение:

0.18S +

15.9374

= 200 000.

Решив последнее уравнение, находим цену покупки:

S = 823 908.50 руб.

6.7. Используем Excel 127

6.7. Используем Excel

Как следует из материала, изложенного ранее в этом разделе, количе-

ственный анализ регулярных потоков платежей сводится к вычислению

следующих основных его характеристик:

— текущая величина потока платежей,

— будущая величина потока платежей,

— величина отдельного платежа,

— норма доходности (процентная ставка),

— количество периодов проведения платежей.

В Excel имеется девять встроенных функций для вычисления этих ха-

рактеристик. Эти функции, как и большинство финансовых функций в

Excel, содержатся в Пакете анализа, поэтому перед выполнением примеров

и упражнений из этого раздела проверьте, что этот пакет установлен на

вашем компьютере

Многие финансовые функции имеют одинаковые аргументы из неболь-

шого, фиксированного набора. Для удобства чтения данного пункта ниже

в таблице приведен список аргументов, которые используются функция-

ми, осуществляющими анализ инвестиций.

Аргумент Назначение

ставка процентная ставка

кол_пер количество периодов проведения операции

период порядковый номер периода

(от 0 до кол_пер)

платеж величина периодического платежа

нач_сум начальная су мма

буд_ст будущая стоимость

тип тип начисления процентов

(1 — начало, 0 — конец периода)

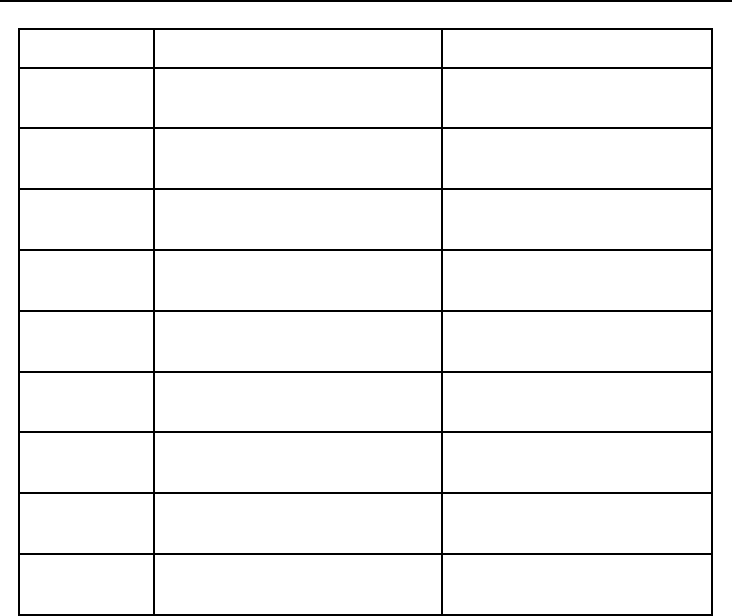
Приведем теперь таблицу, в которой содержатся имена функций (в ру-

сифицированной и англоязычной версиях) анализа регулярных потоков,

их аргументы и вычисляемые величины:

Если Excel установлен у вас в полном объеме, то Пакет анализа всегда доступен.

128 6. Финансовые ренты

Функция Аргументы Вычисляемая величина

БЗ (ставка;кол_пер;платеж будущая величина

FV [;нач_сум][;тип]) потока

КПЕР (ставка;платеж;нач_сум количество выплат

NPER [;буд_ст][;тип])

НОРМА (кол_пер;платеж;нач_сум процен тная ставка

RATE [;буд_ст][;тип][;прогноз])

ППЛАТ (кол_пер;платеж;нач_сум величина периодического

PMT [;буд_ст][;тип]) платежа

ПЗ (ставка;кол_пер;платеж; современная ценность

PV [;буд_ст][;тип]) потока платежей

ПЛПРОЦ (ставка;период;кол_пер; выплата по процентам

IPMT нач_сум;буд_ст[;тип]) в указанный период

ОСНПЛАТ (ставка;период;кол_пер ; величина основного

PPMT нач_сум;буд_ст[;тип]) платежа в указанный период

ОБЩПЛАТ (ставка;кол_пер;нач_сум; сумма накопленных

CUMIPT нач_пер;кон_пер;буд_ст;тип) процентов

ОБЩДОХОД (ставка;кол_пер;нач_сум; накопленная сумма

CUMPRINC нач_пер;кон_пер;буд_ст;тип) погашенного долга

С помощью данных функций можно легко решить не только ранее

разобранные примеры из этого раздела, но и выполнить вычисления в си-

туациях, трудных для ручного счета даже с помощью калькулятора. При-

мером такой ситуации является необходимость определения срока пога-

шения долга, взятого на определенных условиях. Рассмотрим конкретный

случай.

Пример 6.11. Г-н Сидоров получил заем в размере 100 000 руб. под

8% годовых и согласен выплачивать ежемесячно по 2 000 руб. в счет его

погашения. Сколько месяцев потребуется для выплаты всего заема?

Решение . В приведенной выше таблице находим функцию КПЕР, ко-

торая определяет необходимое для погашения заема количество выплат.

Введем в любу ю ячейку формулу:

=КПЕР(8%/12;-2000;100000)

и определим, что для выплаты заема потребуется 61 месяц. Для того что-

бы иметь возможность решать этот пример с другими данными (напри-

Упражнения 129

мер, может измениться процент, под который предоставляется кредит),

следует использовать в формуле в качестве параметров не числа, а отно-

сительные адреса.

На рис. 7 приведен фрагмент рабочего листа с решениями примеров

6.1, 6.3 и 6.11, в которых использовались функции БЗ, ППЛАТ и КПЕР с

относительными адресами ячеек.

Сделаем некоторые замечания, касающиеся применения функции КПЕР.

Аргумент платеж может оказаться слишком мал, чтобы можно было вер-

нуть заем. В этом случае в ячейке с формулой появится сообщение об

ошибке: # ЧИСЛО!. Для возврата заема необходимо, чтобы ежемесячные

выплаты были больше соответствующей процентной ставки, умноженной

на полную величину заема. В рассмотренном примере величина ежеме-

сячных выплат должна быть больше 666 руб.

Обратим внимание читателя на важное правило, которое следует со-

блюдать при задании аргументов, являющихся суммами денег. Оно каса-

ется всех функций из таблицы.

Если некоторые суммы денег являются платежами (расходами), то

соответствующие аргументы должны указываться со знаком минус. Знак

минус можно указывать либо в ячейках с данными, либо в формуле перед

соответствующими аргументами. Например, в примере 6.1 (рис. 7) вели-

чина платежа в ячейке B7 указана со знаком минус, а в примере 6.11

минус указан в формуле в ячейке B31 перед вторым аргументом.

Если значением формулы является величина платежа (как в примере

6.3 на рис. 7), то это значение выдается также со знаком минус. На экране

монитора в этом случае и число, и знак минус перед ним выделяются

красным цветом.

Упражнения

1. Торговая фирма вкладывает 25 000 руб. в конце каждого года в банк, вы -

плачивающий проценты по ставке 5% годовых (сложных). Какая сумма

будет на счет у фирмы: а) через 3 года, б) через 10 лет?

2. Решите упражнение 1 в предположении, что фирма делает вклады в конце

каждого квартала, и ба нк выплачивает проценты по ставке j

= 5%.

3. Фермер хочет накопить за 6 лет 40 000 ру б. для покупки трактора, делая

ежегодные равные вклады в банк, который выплачивает проценты по став-

ке i = 10% годовых (сложных). Какую сумму ежегодно должен фермер

вкладывать в банк?

130 6. Финансовые ренты

Рис. 7. Примеры анализа потока платежей

Упражнения 131

4. Решите упражнение 3 в предположении, что фермер делает ежемесячные

вклады в банк, который выплачивает проценты по ставке j

= 5%.

5. Акционерное общество по производству радиотехники образовало фонд

для покупки техники, вкладывая в него ежегодно 300 000 руб. При этом

каждое полугодие оно делает равные вклады в банк, который выплачивает

5% годовых (сложных). Какая сумма будет на счету АО через 4 г ода?

6. Какую сумму должно вкладывать АО из предыдущего упражнения еже-

годно, если ему необходимо накопить за 4 года 2 млн. руб .?

7. Предприятие создает фонд для постройки нового здания, вкладывая в

него каждые 4 года 15 млн. руб. Деньги кладутся в банк, выплачивающий

5% годовых (сложных). Какая сумма будет в фонде через 16 лет?

8. Какую сумму должно вкладывать в банк предприятие в условиях преды-

дущего упра жнения, чтобы через 20 лет накопить 1 20 млн. руб., необхо-

димых для постройки здания?

9. Судос троительная фирма кла дет в конце каждого года 120 000 руб. в банк,

который выплачивает сложные проценты по ставке j

= 8 %. Какую сумму

накопит фирма за 10 лет?

10. Какую сумму должна класть в банк в конце каждого года фирма из преды-

дущего упражнения, чтобы за 10 лет накопить 2 млн. руб.?

11. Фирма из упражнения 9 желает вносить в банк ежеквартально по 30 000 руб.

Какую сумму она накопит за 10 лет ?

12. Какую сумму должна вносить ежеквартально фирма из упражнения 9,

чтобы за 15 лет накопить 3 млн. руб.?

13. Банк выплачивает на вложенные в него деньги проценты по ставке j

3%. Клиент вкладыва е т в этот банк ежегодно 800 руб., делая равные вкла-

ды в конце каждого квартала. Какая сумма будет на счету э того клиента

через 5 лет?

14. Какую сумму должен вкладывать ежегодно клиент из предыдущего упраж-

нения, чтобы за 6 лет накопить 6 000 руб.?

15. Банк на вложенные в нег о деньги начисляет непрерывные проценты по

ставке (силе роста) δ = 8%. Клиент вкладывает в этот б анк в конце каж-

дого года 500 руб. Какая сумма будет на его счету через 7 лет 6 месяцев?

16. Клиент из предыдущего упражнения хочет вносить ту же годовую сум-

му поквартально равными взносами. Какую сумму он накопит з а 7 лет

6 месяцев?

17. Владелец мастерской вкла дывает каждые 2 года по 1.5 тыс. руб.в банк

из упражнения 15, накаплива я деньги для покупки обо рудования. Какую

сумму он накопит за 6 лет?