Бугров В.Г. Электромеханические переходные процессы в системах электроснабжения
Подождите немного. Документ загружается.


22
Рис.4.3. Схема замещения электрической системы с узловой точкой.
Из анализа множества изменяющихся параметров режима следует,
что существенной независимой переменной, определяющей состояние всех
элементов системы, является напряжение в узловой точке U
k
= var (пере-
менная δ в данном случае не существенна, т.к. она не определяет состояние
нагрузки).
Избыточная энергия системы, возникающая из-за возмущающих
воздействий, проявляется как изменение баланса реактивной мощности уз-
ла
ΔQ = Q
г рез
– Q
н
, (4.4)
где Q
г рез
= Σ Q
г i
– суммарная генерируемая реактивная мощность в
узле.
Взаимосвязь этих существенных переменных в установившемся ре-
жиме определяется уравнением:
(
)
()
(
)
Uxx
Q
U
Е
крезГрезГ
Г
к
qээ
P /2^2^
..
++=
∑
∑
=
=
n
i
ГiрезГ
xx
1
.
;
xx
EЕ
резГГi
n
i
qiqээ
.
1
/
∑
=
=
;
∑
=
=
n
i
Гi
P
P
1
Практический критерий статической устойчивости такой системы
имеет вид:
D(Q
г.рез
-Q
н
)/ dU
к
<0.
Он характеризует реакцию системы на изменение напряжения в узле.
Появление небаланса реактивной мощности в узле рассматривается как
малое возмущение, под действием которого изменяется напряжение.
Исследование системы уравнений по этому критерию заключается в
анализе по переменной U
к
уравнений установившегося режима:
(
)
хх
P
U
Е
U
Q
резгрезк
qээ
К
резГ
.
2
2
2
2
2
.
/
⎟
⎠
⎞
⎜
⎝
⎛
−+−= (4.5)
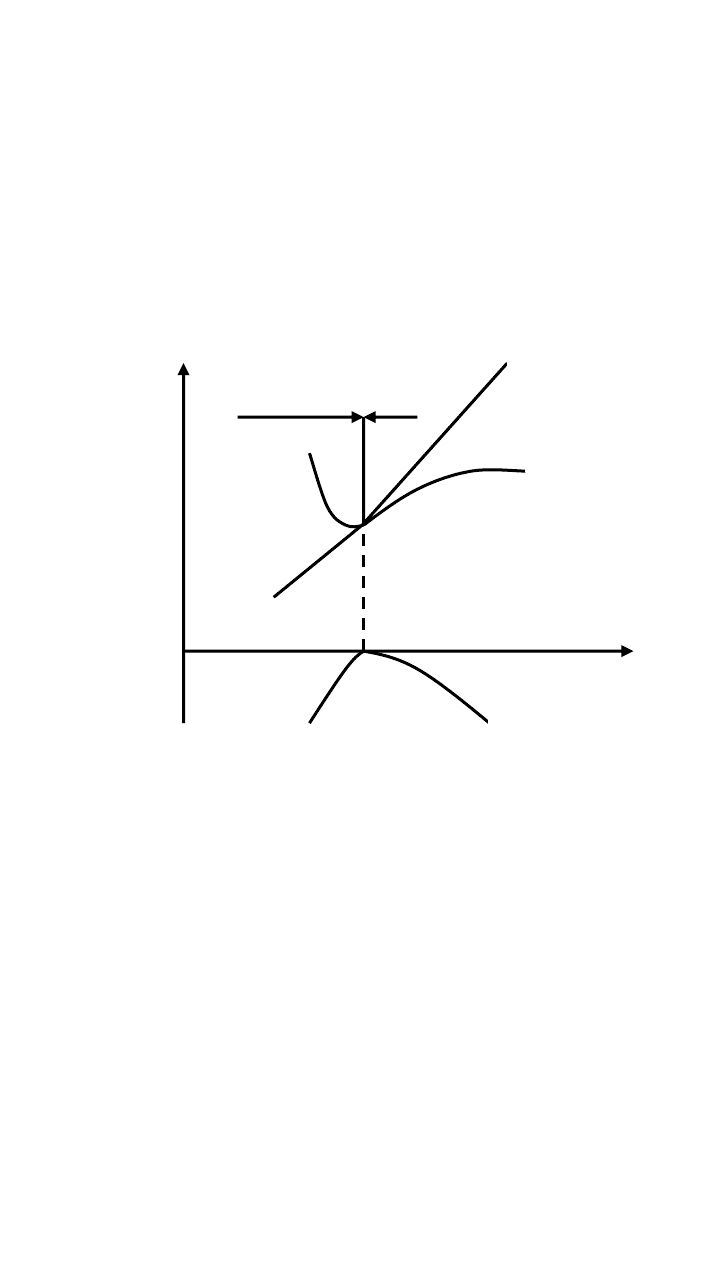
23
(
)
U
F
Q
к
Н
2
=
(4.6)
Систему уравнений решают аналитически или графически в зависи-
мости от способов задания статической характеристики нагрузки. Решение
соответствует следующим критическим значениям существенных пара-
метров режима: U
к.кр
и d∆Q/dU
к
=0 (рис. 4.4). На основе результатов вычис-
лений строят кривую небаланса реактивной мощности ∆Q(U
к
), на которой
выявляют экстремальную точку критического напряжения.
U
к.кр.
Коэффициент запаса статической устойчивости определяют через по-
казатели установившегося и предельного режимов:
К
зап.u
=(U
к
-U
к.кр
)100/U
к
Питание асинхронной нагрузки от мощной ЭЭС. Предполагается, что
последняя обладает бесконечной мощностью и имеет узловую точку неиз-
менного напряжения. В этом случае действие возмущений влияет только
на баланс активной мощности в точке включения нагрузки, Нарушение ко-
торого можно оценить по критерию
d(P
мех
-P)/ds<0,
где Р – электромагнитная мощность асинхронной нагрузки, Р
мех
–
мощность, определяемая моментом сопротивления рабочего механизма.
При Р
мех
(s)=const получаем:
dP/ds>0.
Q,
∆Q
d/dU
к
*∆Q>0 d/dU
к
∆Q<0
Q
н
=F(U
к
)
Q
2Σ
(U
к
)
d/dU
к
*∆Q=0
0
∆
Q(
U
к
U
к
Рис.4.4. Графическое решение системы уравнений (4.4;4.5;4.6.)
24
Система электроснабжения с эквивалентным источником, питаю-
щим комплексную нагрузку соизмеримой мощности.
В точке включения
нагрузки состояние равновесия характеризуется изменяющимися парамет-
рами режима U,Р
и
=F
1
(U), Q
н
=F
2
(U). В данном случае существенной пере-
менной является напряжение в узле подключения нагрузки, которое отра-
жает состояние всех элементов системы. Изменение всех переменных па-
раметров режима можно зафиксировать по показателям режима Е
эк
и Q
эк
,
по которым судят об избыточной энергии системы при возмущении.
Графический анализ зависимости
()
(
)()
U
r
Q
х
Р
х
Q
rР
U
Е
эк
н
эк
н
эк
н
экнэк
/2^2^
'
2
−+++=
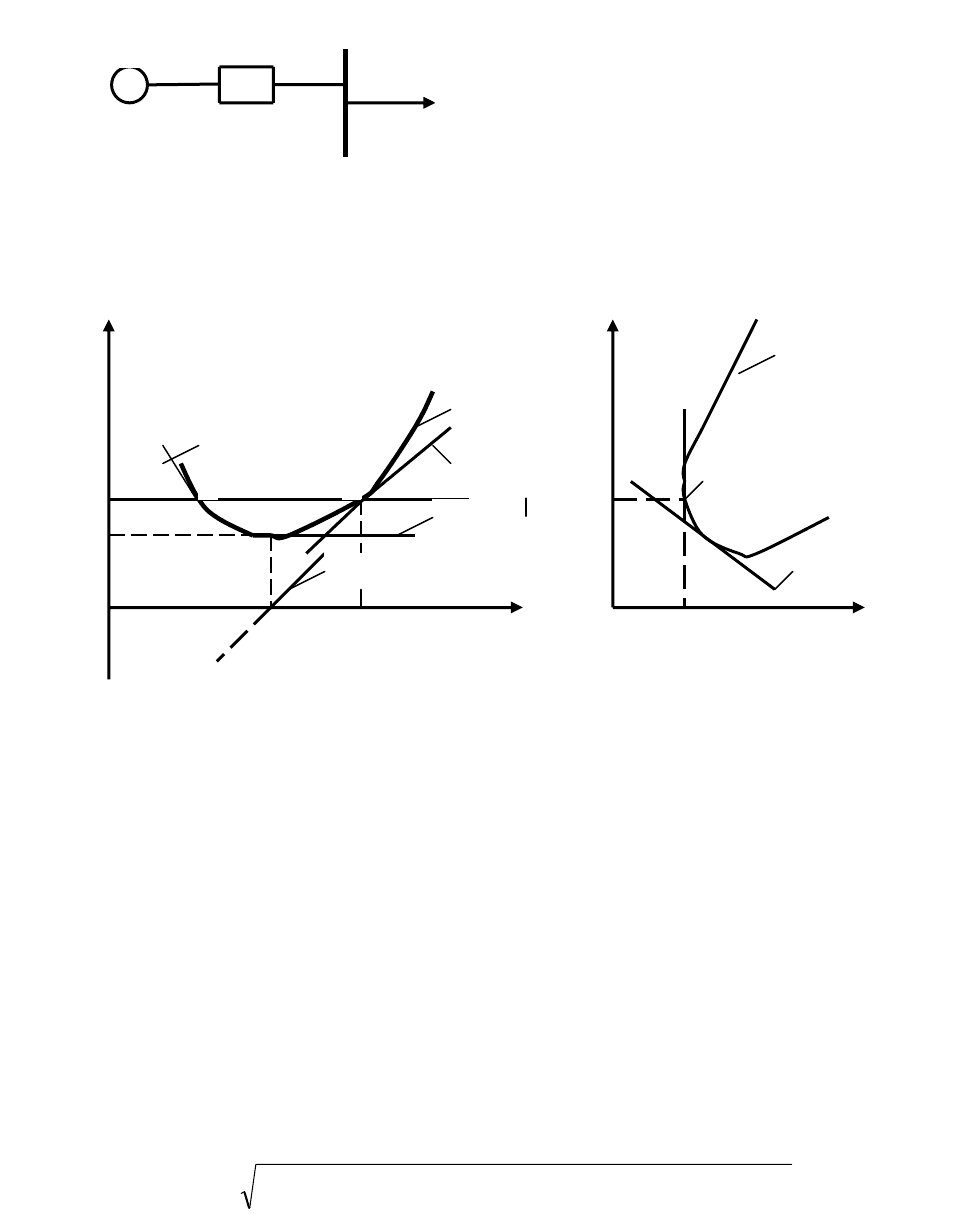
с утяжелением режима по переменной U показывает, что она имеет
минимум при dЕ
эк
/dU>0 с координатами, соответствующими предельному
режиму Е
эк min
, U
кр
(рис. 4.5.)
Критерий статической устойчивости в данном случае имеет вид
Рис. 4.5. Схема замещения СЭС комплексной нагрузкой (а) и зависимо-
сти её существенных переменных (б,в)
Е
эк
dЕ
эк
/dU<0
b a
Е
эк
(U)
dЕ
эк
/dU>0
dЕ
эк
/dU<0
dЕ
эк
/dU(U)
U
кр
U
0
0
U
Е
эк min
Е
эк0
б
Q
эк
0
Q
эк
(U)
dQ
эк
/dЕ
эк
= -∞
Е
эк.кр
Е
эк
в
Е
эк
R
эк
+jx
эк
U
Р
н
=F
1
(U)
Q
н
=F
2
(U)
ω
0
=const
a
dQ
эк
/dЕ
эк
<0
25
dE/dU>0 ( критерий устойчивости Жданова).
4.2. Исследование статической устойчивости
методом малых колебаний.
В отличие от оценки статической устойчивости по практическим кри-
териям суть этого метода заключается в исследовании уравнений движе-
ния, записанных в виде уравнений малых отклонений.
При установлении простейших условий статической устойчивости
(практических критериев) ответ получается только в форме «да - нет»,
«уйдёт – не уйдёт» режим изначального состояния при малом возмущении
системы
. При установлении критериев устойчивости, основанных на ис-
следовании уравнений движения – уравнений малых колебаний (малых от-
клонений), физическая природа происходящих явлений выясняется более
полно: устанавливается в любом случае (устойчивость, неустойчивость)
характер движения (апериодическое, колебательное – затухающее или на-
растающее).
Электрическая система при изучении переходных процессов описыва-
ется системой нелинейных дифференциальных уравнений вида
Σ(А
ij
d
2
х
i
/dt
2
+B
ij
dx
i
+C
ij
)=F
j
(t).
Коэффициенты А, В и С – действительные. Они определяются пара-
метрами системы и нелинейными функциями Ф(х
i
) от переменных Х
i
, ха-
рактеризующих состояние системы в каждый момент времени; F
j
– внеш-
ние (возмущающие) силы, переменные во времени, отражающие измене-
ние внешних условий системы.
При F
j
(t)=F
j0
система имеет решение
X
i
(t)=x
i0
;
Dx
i
/dt=0;
D
2
x
i
/dt
2
=0;
ΣC
ij
x
i0
=F
j0
.
Это решение соответствует состоянию равновесия, т.е. определяет па-
раметры установившегося режима электрической системы. При изучении
статической устойчивости рассматриваются переходные процессы при ус-
ловии малости отклонения всех переменных и внешних сил от состояния
равновесия. Математически это условие записывается так:
F
j
(t) – F
j0
=f
j
(t);
X
i
(t) – x
j0
=∆x
i
;
Dx
i
/dt=d∆x
1
/dt;
D
2
x
i
/dt
2
=d
2
∆x
i
/dt
2
.
26
Нелинейные функции Ф(x
i
), входящие в коэффициенты исходной сис-
темы уравнений, линеаризуется в точке, соответствующей состоянию рав-
новесия. Эта процедура заключается в разложении нелинейной функции в
ряд Тейлора, оставляет только линейные члены этого ряда.
Приведя линеаризацию по первому приближению, перейдём от сис-
темы нелинейных дифференциальных уравнений к системе линеаризован-
ной – линейной. Решение таких систем
уравнений с помощью так назы-
ваемого
характеристического уравнения известно из математики.
Будем далее пользоваться им, изучая процессы при действии внешних
сил, меняющихся во времени:
Σ(а
ij
d
2
x
i
/dt
2
+b
ij
dx
i
/dt+c
ij
∆x
i
)=f
j
(t).
Коэффициенты a,b,c включают в себя частные производные
(ðФ/ðх
ixi0
), взятые в точке исходного режима.
С помощью линеаризованных уравнений изучаются переходные про-
цессы:
- вынужденные, при действии внешней – возмущающей силы;
- свободные, после возникновения начальных отклонений и исчезно-
вения внешней силы, вызвавшей эти отклонения.
В первом случае при f
j
(t)≠0 ротор под действием заданной, например
малой синусоидальной возмущающей, постоянно действующей силы со-
вершает малые колебания.
Во втором случае ротор генератора, получивший под действием ка-
кой-то (не фиксированной) внешней (возмущающей) силы отклонение от
положения равновесия, т.е. от угла δ
0
на ∆δ, будучи предоставлен дейст-
вию только внутренних сил, будет совершать те или иные движения, «воз-
вращаясь» или «уходя» от положения равновесия δ
0
. При заданной внеш-
ней возмущающей силе f
j
(t) ≠0 условия статической устойчивости отлича-
ются от условий динамической устойчивости малостью, которая настолько
мала, что процесс практически
не зависит от её значения и места прило-
жения
f
j
(t). Это обстоятельство отражено в решении линеаризованного
уравнения,
из характеристического уравнения которого влияние значения
возмущения и места приложения его,
реально существующие, - в силу
сделанных допущений
исчезли.
Оценка устойчивости нелинейной системы возможна по виду корней
линеаризованных уравнений. Это было обосновано известным русским ма-
тематиком А.М. Ляпуновым. Им был предложен (1893) так называемый
метод первого приближения, предназначенный для обоснованного иссле-
дования тех линейных (линеаризованных) уравнений движения системы,
которые получаются после разложения в ряд линейной функции, Находя-
щейся в правой
части исходного уравнения. Для теоремы Ляпунова дали
строгое обоснование уравнений первого приближения.
27
Теорема 1 утверждает, что при характеристическом уравнении перво-
го приближения, имеющем корни только с отрицательными вещественны-
ми частями, невозмущённое движение устойчиво, и при том асимптотиче-
ски, каковы бы ни были нелинейные функции в правой части исходного
уравнения.
Теорема 2 утверждает, что если в числе корней характеристического
уравнения первого приближения имеются корни, вещественные части ко-
торых положительны, то невозмущённое движение неустойчиво, каковы
бы ни были нелинейные функции в правой части исходного уравнения.
Случай, когда характеристическое уравнение не имеет корней с поло-
жительной вещественной частью, но имеет хотя бы один корень с
нулевой
вещественной частью, является особым случаем.
В особых случаях по кор-
ням характеристического уравнения линеаризованной системы нельзя сде-
лать заключение об устойчивости исходной системы. Для получения тако-
го заключения необходимы дополнительные исследования вида нелиней-
ной функции.
4.2.1. Нерегулируемая система, рассмотренная без учёта электро-
магнитных переходных процессов.
Частный случай, когда в системе предполагается отсутствие регули-
рования возбуждения и не учитываются переходные процессы, представ-
ляется интерес для выяснения влияния этих факторов на предел переда-
ваемой мощности. Частный случай позволяет также выявить зависимость
характера процесса от начального режима.
Пусть система представлена схемой на
рис.4.6,а. Учтём демпферный
момент упрощённо, введя в уравнение движения член, пропорциональный
производной угла с постоянным коэффициентом P
d
.
В этой идеализации переходные процессы в электрической системе
будут описываться одним нелинейным дифференциальным уравнением
второго порядка
Т
j
p
2
δ+P
d
=P
т
- Р
эл.
Здесь P
т
=Р
0
=Р
m
sinδ
0
– мощность турбины, определяющая исходный
установившийся режим электрической системы (Р
0,
δ
0
) (рис. 4.4.), статиче-
ская устойчивость которого подлежит проверке; Р
эл
= Р
m
sinδ – электромаг-
нитная мощность синхронного генератора, являющаяся нелинейной функ-
цией одной переменной – угла δ.
Раскладывая Р
m
sinδ – в ряд Тейлора по малой величине ∆δ в окрестно-
сти δ
0
(т.е. полагая δ= δ
0
+∆δ ) и оставляя только два (нулевой и линейный)

28
члена разложения или, что то же самое, заменяя участок синусоиды в ок-
рестности δ
0
касательной, получим
Т
j
p
2
∆δ+P
d
p∆δ= Р
m
sinδ
0
- Р
m
sinδ
0
- dР
Эл
/dδ) ∆δ. (4.7)
Введя обозначение с
1
=d Р
эл
/dδ=(E
q0
U/x
dΣ
) cosδ
0
, получим линеаризо-
ванное по
первому приближению дифференциальное уравнение
Т
j
p
2
∆δ+P
d
p∆δ+с
1
∆δ=0 (4.8)
Величина с
1
(которую иногда называют синхронизирующей мощно-
стью) зависит от исходного режима и становится равной нулю в режиме,
соответствующем Р
m
(δ
0
=90°).Уравнение (4.7) имеет решение
∆δ=А
1
е
p1t
+A
2
e
p2t
Характеристическое уравнение для (4.8)
Т
j
p
2
+P
d
+ с
1
=0
а
)
х
с
Е U
Р
б
)
Tgε=c
1
=dP/dδ
∆P=c
1
∆δ
1
ε
P
эл
=φ(δ)
с
1
=dP/dδ
∆δ
δ
0
+∆δ
с
1
=0
δ
P
0
P
0
+∆P
Рис. 4.6. Основные соотношения при малых колебаниях простейшей системы:
а – схема; б – характеристика.

29
имеет два корня:
где
)/(
2
1
αγ
−=
j
Tc
- собственная частота колебаний ротора синхронной
машины,
)2(
/
T
P
j
d
−=
α
– декремент затухания.
При с
1
>0 система всегда будет устойчива. При с
1
/Т
j
<α
2
оба корня бу-
дут действительные отрицательные, процесс будет устойчивым, угол на-
грузки изменяется по экспоненциальному закону. При с
1
/Т
j
> α
2
оба корня
будут комплексными с отрицательными вещественными частями, процесс
будет устойчивым, характер процесса колебательный.
При с
1
<0 соотношение между с
1
/Т
j
и α не влияет на характер процесса.
Один корень всегда будет положительным, а другой отрицательным. Про-
цесс будет неустойчивый, угол нагрузки изменяется по экспоненциально-
му закону.. При с
1
=0 появляется один нулевой корень и один корень, рав-
ный –Р
d
/Т
j
. Наличие нулевого корня указывает, что для выяснения дейст-
вительного поведения системы нужно или провести дополнительные ис-
следования с учётом уточняющих факторов, или считать, что практически
система может получить некоторый единичный толчок, который приведёт
к нарушению устойчивости.
Рассмотрим устойчивость
без учёта электромагнитных переходных
процессов в контурах ротора и без учёта демпферного момента
(Р
в
=0).
Это частный случай, соответствующий исследованию простейшей системы
как консервативной, приводит к характеристическому уравнению
Т
j
р
2
+ с
1
=0, которое имеет два корня:
и всякое возмущение в системе будет приводить к незатухающим колеба-
ниям с собственной частотой, если с
1
>0 и оба корня мнимые.
Самораскачивание и самовозбуждение. Проведенное исследование
статической устойчивости было недостаточно полным, так как в нем не
рассматривались нарушения устойчивости, имеющие характер самораска-
чивания и самовозбуждения. Такие нарушения могут наступать при нали-
чии в сети, связывающей исследуемую станцию (эквивалентный генера-
(
)
Tc
р
j
j
/
1
2,1
±=
(
)
()
{}
(
)
,
2
/
2/
2/
2/
4
2
1
1
2
2,1
αγ
+±=−+−−±=
=
⎟
⎠
⎞
⎜
⎝
⎛
−±−=
j
dd
T
PTP
T
c
Тc
TPP
р
j
j
j
jdd
30
тор) с системой (в частности с шинами бесконечной мощности), или за-
метного активного сопротивления (r/x>0,05), или значительной емкости (-
Т
d
).В первом случае возникают установившиеся или нарастающие колеба-
ния -
самораскачивание, во втором происходит самопроизвольный рост
тока и напряжения генераторов, потребляющих емкостную реактивную
мощность, -
самовозбуждение.
4.2.2. Математические критерии устойчивости
Об устойчивости нелинейной системы судят по затуханию переход-
ного процесса, наличие которого устанавливают по виду корней характе-
ристического уравнения системы:
a
0
p
n
+a
1
p
n-1
+a
2
p
n-2
+…+a
n-1
p +a
n
=0.
Для устойчивости необходимо и достаточно чтобы корни характери-
стического уравнения имели отрицательные вещественные
части.
Наличие у корней отрицательной вещественной части можно устано-
вить прямым решением уравнений не выше четвертого порядка. При ана-
лизе уравнений более высоких порядков используют математические кри-
терии устойчивости, которые не требуют нахождения значений корней ха-
рактеристического уравнения.
Применяемые математические критерии устойчивости делятся на
ал-
гебраические
(Гурвица, Льенара –Шипара, Рауса) и частотные (Михайло-
ва, Найквиста, логарифмический). Используется также метод D - разбие-
ния. При этом выполняется анализ взаимосвязей отрицательного знака ве-
щественной части корней характеристического уравнения с его коэффици-
ентами a
i
(i=0,n). Необходимым, но недостаточным признаком устойчиво-
сти невозмущенного движения является наличие одинакового знака у ко-
эффициентов характеристического уравнения. Этот необходимый признак
устойчивости является достаточным для уравнений первого и второго по-
рядка.
5. ПРИБЛИЖЕННЫЕ МЕТОДЫ АНАЛИЗА ДИНАМИЧЕСКОЙ
УСТОЙЧИВОСТИ
Задачами анализа динамической устойчивости СЭС являются оценка
характера переходного процесса при сильных возмущениях, установление
критических параметров при изменении режима, а также расчет сущест-
венных параметров режима при переходе из одного состояния в другое.
Для решения этих задач используются приближенные методы, поскольку
точная оценка динамической устойчивости при учете всех переходных
31
процессов и изменений в СЭС, связанных с сильными возмущениями,
весьма сложна.
Приближенные методы анализа динамической устойчивости СЭС ос-
новываются на ряде допущений:
1)
мгновенное изменение электрической мощности при смене режимов;
2)
незначительное отклонение частоты вращения роторов генераторов от
синхронной;
3) неизменность вращающего момента первичных двигателей;
4)
ограниченный интервал времени протекания переходного процесса;
5)
сохранение симметрии трёхфазной системы источников при её наруше-
нии в электрической сети;
6) учёт только основных нелинейных характеристик и др.
Уровень принимаемых допущений должен соответствовать конечной
цели решаемой задачи. С этой точки зрения приближённые методы можно
разделить на
упрощённые и уточнённые, отличающиеся уровнем прини-
маемых допущений.
Уточнённые методы учитывают ряд факторов, не принимаемых во
внимание в упрощённых методах, но оказывающих существенное влияние
на переходный процесс:
⎯ автоматическое возбуждение, изменяющего ЭДС генераторов и, следо-
вательно, их электромагнитный момент;
⎯
автоматическое регулирование частоты вращения первичных двигате-
лей и их вращающий момент;
⎯
дополнительные тормозные моменты, возникающие в процессе КЗ от
периодической составляющей тока статора и токов, наводимых в успокои-
тельных обмотках ротора;
⎯
динамические характеристики узлов нагрузки.
Основными
упрощёнными методами анализа динамической устойчи-
вости СЭС являются:
⎯
метод площадей, используемый для определения предельных значений
угла и времени отключения КЗ;
⎯
численное решение нелинейных дифференциальных уравнений мето-
дом последовательных интервалов, применяемое для качественной оценки
характера переходного процесса по изменению угла нагрузки во времени.
