Brewster H.D. Fluid Mechanics
Подождите немного. Документ загружается.


292
Wave Motions in Fluids Freefrom Viscosity
With the above listed equations gravitational waves and capillary waves
can be treated, which usually represent small amplitudes.
PLANE
STANDING
WAVES
When considering wave motions, where the fluid particles move only in
parallel to the xl - x
2
-plane,
i.e.,
where the pressure P and the velocity
~
are
independent
of
x3
' so that the fluid motions in all areas parallel to the X I - x
2
-
plane take place
in
the same way, a plane wave motion with the following
potential results:
<I>(x,
y.
I) =
<I>(x,
y) cos(
<pI
+
E)
For the case
of
a standing wave to be dealt with in this section it stated:
<I>(x,
y) =
P(y)
sin[k(x-;)]
p
The potential
<I>
fulfills the Laplace equation.
a
2
<1>
a
2
<1>
-2+-2
=0
ax
By
a
2
<1>
2 . a
2
<1>
d
2
P
Mit
p-
=
-P(y)k
sln[k(x-;)]
and
P-2
=
P-sin[k(x-;)]
ax
2
By
di
one obtains the following differential equation:
d
2
P
_k2p
= 0
di
the solution
of
which is as follows:
y
P(y) = C
1
exp(ky) + C
2
exp(-ky)
fur -
00
~
y
~
0 -
00
~
+ x
~
+
00
"... c
2
exp (- ky)
'.
".
Fig. Illustration
of
the Decrease for y
--+
-
00
x
The
integration
COl1stant C
2
,
when
carrying
out
more
precise
considerations, results as C
2
=
0,
as otherwise
fOl
large depths y =~ -
00
the
P (y)-term would become very big, so that the solution:
<I>(x,y)
=
~l
exp(ky)sin[k(x-;)]

Wave Motions in Fluids Free from Viscosity
can
be
obtained,
or
<I>(X,
y,
t) =
~I
exp(ky)sin[k(x-~)]cos(cpt+
E)
293
When starting from the assumption that the occurring fluid motion is slow,
the equation
a<l>
P 1 2
-+-+-U·
+
gTJ
= 0
at
p 2 J
for y =
TJ
can
be
written as follows:
8<1>
P
- + - +
gTJ
= 0 for y =
TJ
at
p
A derivation to the time yields the relation indicated below, as the pressure
along the free surface does not change:
and
a
2
<1>
8Tj
a
2
<1>
-+g-
=
-+gu2
at
2
at at
2
acp
With u2 =
ay
it results:
When employing to
one obtains:
8
2
<1>
C
-2
=
__
I
exp(ky)sin[k(x-~)]cp2coS(CP+E)
at
p
: = +
~
exp(ky)sin[k(x-~)]cos(cp+
E)
cp2
=
kg
Thus for the remaining considerations the following fluid motion has
to
be examined which for the sake
of
simplicity is considered for
~
= 0 and E =
o.
or
<I>(x,
y, t) =
~I
exp(ky)sin(lex) cos(et)
For
the free surface it is computed from equation:
11
=
-..!..
a<l>
=
-..!..~<I>(x,O,t)
gat
gat
TJ
=
C1cp
sin(lex) sin(
cpt)
g
. h C1CP· (
).
ld
Wit A =
-sm
cpt
It
ho
s:
pg

294 Wave Motions in Fluids Free from Viscosity
T\
= A sin(kx)
m·1t
For x =
-k-
result for m = 0, ±1, ±2, ±
...
nodal points
of
a standing
wave. In the middle between these nodes are the "antinodal points"
of
the
wave motion. The wavelength
of
the sinusoidal fluid motion can be computed
as:
21t
t..=T
The amplitude
of
the wave motion is C
1
<P.
sin(<pt)
= A quency
of
the
g
wave motion it holds:
or
<p
1
j=-=-
21t
T
Taking into consideration and one obtains:
T=
~
=~2;k
g
t..=--
21tj2
yt
2
bzw.
A,=-
21t
The above relations show that the wavelength
of
standing fluid waves
decreases with increasing frequency
of
the motion.
PLANE
PROGRESSING
WAVES
For the considerations stated below it is assumed that the considered fluid
takes up the space as follows:
-
00
:S
Y
:S
0 and -
00
:S
x
:S
+
00
and at the point y = 0 occupies a free surface which for the considerations
carried out possesses a finite surface. The equations required for the treatment
of
progressing waves can be stated
as
follows:
a
2
g a
2
$
-+--0
ax2
ay2-
With Y =
T\(x
1
,
t) for the free surface it holds:
..Q.(Y-T\)
=
0-
u2
=(~+Ul
~)TJ
Dt
at
ax
1
Neglecting the term
of
second order it results:
8$
8TJ
ay=8i

Wave Motions in Fluids Free from Viscosity
295
For the pressure at the free surface it can be stated:
p =
_cr[_1
+_1
]
Rl
R2
where Rl and
~
represent the main radiuses
of
curvature
of
the disturbed
surface and
cr
indicates the surface tension. Linearized it can be written:
a
2
"
p=
-cr-
(}x2
where the pressure above the free surface is formulated with P = 0 Otherwise
P is to be replaced by (P = Po).
For plane progressing waves the following potential can be stated:
<j>(x,
y,
t) = C exp(ky) cos [k
(x
- ct)]
with
<j>
= 0 for y =
-00
The formulation for. fulfills the continuity equation in
the form.
The Bernouilli equation can be stated as follows:
P
8<l>
- =
---gy
p at .
Or transcribed:
From this follows:
and in consideration
of
a
2
<j>
= [cr
~
_
g]
8<l>
at
2
p (}x2
ag
For the left side
of
it can
be
written with:
a
2
<j>
at
2
=-cIc2c2 exp(ky) cos [k(x-ct)] =
--!t2c2<j>
so that it holds:
[
cr
a
2
]
8<l>
1c2c2<j>
= g - P (}x2
By
With : =
k<l>
and
~~
= _k
2
<j>
results from for the velocity
of
the progressing
wave:

296
21t
Wave Motions in Fluids Free from Viscosity
g ko
C2=
-+-
k p
With k = T it can be seen that for long waves the influence
of
the gravity
dominates:
c =
Jf
shear waves
For waves with small wavelengths the capillary e ects dominate:
c =
~
k;
capillary waves
Concerning wavelengths, often the path curves
of
the fluid particles are
also
of
interest, which occur at the water surface
or
in certain depths below
the water surface. In this respect the following considerations can be carried
out, where
Xo
and
Yo
are introduced as the coordinates which
From this result:
Or transcribed:
y
u =
8cI>
=
dx
=Ckexp(ky)sin[k(x-ct)]
x
Ox
dt
u =
Bcj>
= dy
=Ckexp(ky)cos[k(x-ct)]
Y
By
dt
x =
Xo
+ C . k exp(ky) cos [k(x - ct)]
(~~)
y =
Yo
+
ck
exp(ky) sin [k(x - ct)]
(~;)
x
Fig. Circular Paths
of
the Fluid Particle Motion
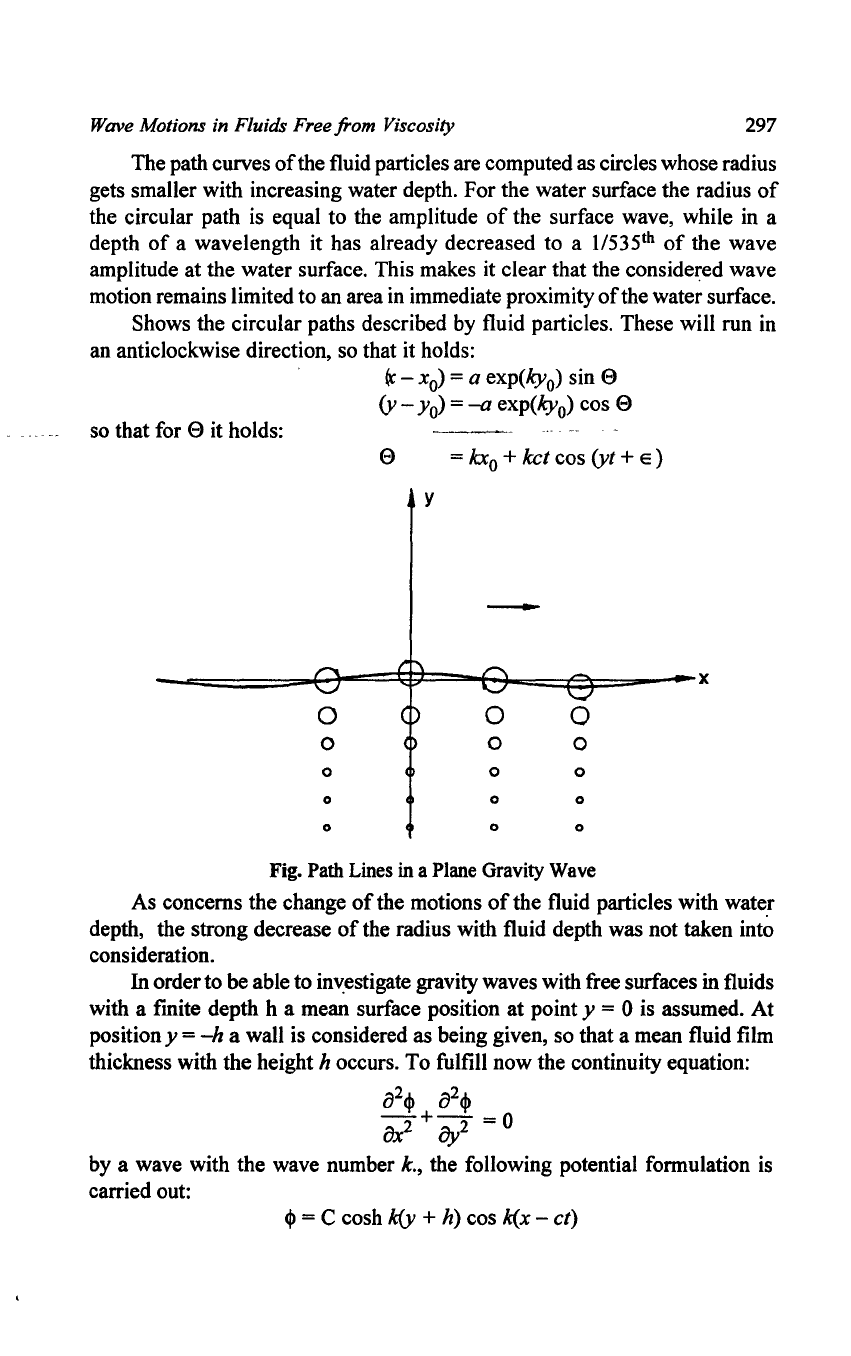
Wave Motions in Fluids Free from Viscosity
297
The path curves
of
the fluid particles are computed as circles whose radius
gets smaller with increasing water depth. For the water surface the radius
of
the circular path is equal to the amplitude
of
the surface wave, while in a
depth
of
a wavelength it has already decreased to a 1I535
th
of
the wave
amplitude at the water surface. This makes it clear that the considered wave
motion remains limited to an area in immediate proximity
ofthe
water surface.
Shows the circular paths described by fluid particles. These will run in
an anticlockwise direction, so that it holds:
so that for
e it holds:
o
o
o
(t
- x
o
) = a exp(kyo) sin e
(v -
Yo)
=
-a
exp(kyo) cos e
e
=
kxo
+ ket cos (vt + E )
y
-
o o
o o
o
o
Fig. Path
Lines
in
a Plane Gravity
Wave
As concerns the change
of
the motions
of
the fluid particles with water
depth, the strong decrease
of
the radius with fluid depth was not taken into
consideration.
In order to be able to inv:estigate gravity waves with free surfaces
in
fluids
with a fmite depth h a mean surface position at point
y = 0 is assumed. At
position
y =
-h
a wall is considered as being given, so that a mean fluid film
thickness with the height
h occurs. To fulfill now the continuity equation:
a
2
cj1
a
2
cj1
ax2+ay2
=0
by a wave with the wave number
k.,
the following potential formulation is
carried out:
cjI
= C cosh k(y + h) cos k(x - ct)

298
Wave Motions in Fluids Free from Viscosity
which does not only fulfill the continuity equation, but permits also to fulfill
the boundary condition at the bottom
of
the fluid layer:
8cI>
ay
= 0 for y =
-h
It then results a condition for the free surface that can be stated as below
indicated:
Icc'
cosh
kh
~
(g
+
k:r
J sinh
kh,
Or resolved to the wave velocity one obtains:
(
k2TJtanhkh
2=
g+--p
k
For
long-waved waves, i.e. for small
values
of
the
wave
number
k one obtains for the wave velocity:
2 = gh.
The waves moving with this velocity are essentially gravitation waves,
as the surface
curvature is so small that the influences
of
the surface tension
at the wave motion are not perceived.
For very short waves, i.e. for large values
of
the wave time k one obtains
on the other hand:
kT
2=
-
P
This
is
the propagation velocity
of
the capillary waves which this equation
shows for the velocity
of
the capillary waves, so that their propagation velocity
is not influenced by the height
of
the fluid layer.
REFERENCES
TO
FURTHER
WAVE
MOTIONS
The wave motions represent introducing considerations that experience
extensions in relevant manuals with emphasis on wave motions.
Nonetheless, manuals with general considerations on wave motions
in
fluids are missing, i.e. the treatment
of
wave motions is always limited
to
the
treatment
of
very special wave motions. The following wave motions in fluids
are dealt with:
• Gerstner waves
• Solitar waves
• Rossby-waves
• Stokes-waves
• Cnoidal-waves
•
Axisymmetric waves

Wave Motions in Fluids Free from Viscosity
299
So
if
one wants to find the introducing literature on the wave motion
observed in nature, it is necessary to perceive the physical causes
0 the
considered wave motion.
Thus one observes for example that a long .body
which
is moved
transversely to its linear expansion near the free surface forms waves mainly
in its wake. In front
of
the body one observes viewed from the amplitude smaller
surface waves, when the dimensions
of
the bodies
in
flow direction are smaller
as compared
to(cr/pg)1I2
Otherwise the gravity waves occurring behind the
body dominate and the capillary waves that can be observed in front
of
the
body are negligible.
So
when one has
~ecognized
the nature
of
the observed
wave motions.

Index
A
Aerostatics 155, 156, 185, 191
Arbitrary
plane
28
Area
changes 231, 234
Atmosphere
6,
11,23,24, 26, 169, 185,
186, 187, 188,
190, 193
B
Balance Considerations 58, 59, 60
Basic
equations
36, 59, 60,
67, 68,
96,
100, 105, 108, 116, 124, 131, 156,
158, 161, 163, 165, 178, 188, 189,
190, 194, 199, 201, 203, 221, 222,
241, 248, 264, 266, 278, 282, 287,
288
Basic laws
4,
7,
45, 59, 61, 68, 95, 160
Bernoulli equation
Ill,
114, 124,126,
127,
204, 206, 207, 209, 214, 215,
227, 229, 231, 248,
270, 273, 274,
276,290
Bubble formation 177, 178, 180, 181,
182, 183, 184
Buoyancy Forces
30, 276
C
Chemical Engineering 1
Chemical Species
7,
41, 59, 95, 96
Circulation 261,266,267,268,269,275,
276,277
Communicating
containers 166, 167,
168
Compensating flows 235, 240, 241, 243,
244
Conservation laws 58, 59, 67, 88, 95
Containers 158, 165, 166, 167, 168, 172,
175
Continuity
equation
59,
73,
83, 100,
105, 109,
115, 116, 117, 125, 132,
155, 194, 195, 196, 198,
201, 204,
206, 207, 209,
211, 214, 216, 218,
223, 224, 225, 229,
230,
231,"
244,
247, 248, 283, 284, 285, 288,
290,
295, 297, 298
Continuum
mechanics 37, 38, 40, 41,
45,47,48
Converging
nozzles 240
Coordinate
systems 116, 117
Crocco
equation
124, 127
Cross-section 179, 211, 221, 224, 225,
230, 231, 233, 234, 235, 239, 241,
242, 243, 244, 245
Curved
surface 15, 29,171,172
Cylinder
2, 4, 21, 22, 23, 30, 32, 33, 34,
162, 163, 164, 165, 175, 188, 189,
253, 256, 257, 263, 264, 265, 266,
268,269,270,275,276,277
D
Deformation
2,
4, 55, 86, 87, 88, 89, 90,
91, 92, 93, 94, 163
Density
7,8,9,
10, 13,23,24,25,26,27,
29, 31, 33, 36, 37, 38, 39,
40, 45, 47,
48,54,57,
61,
64, 65,
66,
67, 68, 97,
223, 224, 225, 231, 232, 233, 234,
243, 244, 245, 276, 279,
280, 281,
285
Derivations
36,
37, 38, 44,
45,
46, 48,

Index
50,51,52,59,65,73,84,85,95,96,
113, 115, 116, 117, 124, 127, 156,
196, 199,
203, 207,
222,
224,
241,
270,282,287
Dipole current flow 262,263,264,265,
266,267
Divergence 84,
85,
86,89,99, 100, 125
E
Edge 29, 45, 85,
209
Elevation
2,
17,
20, 21,
22, 25,
26, 27,
32,33
Energy 1,
2,
7,
14, 15,20,36,40,44,49,
53,54,55,
60, 61, 63,
65,
67, 69,
92,
129, 131, 155, 156, 160, 169, 172,
206, 221, 222, 223, 230, 231,
232,
235,280,282,283,284,285,286
Equation
8,
25, 60, 97, 101, 109, 111,
114, 115, 126, 127, 129,
130,
131,
216, 217, 223, 224, 225, 226, 227,
231, 247, 251, 283
Exit Velocity
204
F
Flow field 37, 50,
69,
70, 71, 73, 75,
77,
78,83,84,85,86,87,88,89,90,
107,
248, 249, 250, 252, 256, 261,
262,
267,268,269,273
Flow forces 273,274,275
Flow lines
77,
78,
79,
80,
81,
82,
214,
221, 249, 250, 251, 252, 256, 258,
259, 261, 263,
270
Fluid elements 36, 38,
60, 68, 69,
70,
71, 72,
77,
81, 86, 87,
89,
90, 91, 96,
97, 98, 157, 167, 170, 222
Fluid Hydrostatics 24
Fluid mechanics 1,
4,
6,
7,
35, 36,
37,
38,39,40,41,58,59,60,63,67,68,
69,73,90,95,96,101,104,108,
129,
131,165,171,246,266,278,282
Fluids 1,
3,
4,
5,
6,
8,
12, 13, 35, 36,
37,
38,
39,41,44,50,55,56,57,61,64,
180, 182, 185, 190, 228, 246,
247,
285, 287, 290, 297, 298
301
Force
1,
2,
4,
5,
6,
8,
11, 12, 14,
15, 17,
18,19,20,21,22,27,28,29,30,31,
209, 210, 213, 214, 215, 216, 229,
270,273,274,275,276
Free fluid surfaces
170
G
Gas
3,
8,
9,
10, 11, 13,
18, 25,
26,
28, 36,
37,40,44,45,47,48,50,51,52,54,
172,
173, 177, 178, 180, 181, 182,
185, 193,
201,
203, 236, 237, 245,
279,284
General Solution Set-up 287
H
Heat
13,
36, 41, 42,
44,
48, 51, 52, 53,
63,64,65,66,67,111,112,113,114,
115,192,199,202,228,282,284
Horizontal pressure 6
Hydro-Mechanical
229
Hydrostatic Force
29
Hydrostatics 156, 157, 158, 160, 163,
185,
189,
191
I
Incompressible Flows 229,
231
Instruments 165, 167
Integral
23,
27,
29,
38, 41, 57, 59,
60,
98, 179, 186, 194, 195, 197, 198,
208, 211, 212, 214, 216, 218, 219,
221, 223, 224, 229,
270, 274, 275,
277,278
J
Jet Deflection 209
K
Kinematic Quantities 77
L
Liquid
3,
8,
13, 14,
15,
16, 17, 18,
23,
27,28,29,30,31,32,33,34,35,36,
