Brewster H.D. Fluid Mechanics
Подождите немного. Документ загружается.

222
Stream Tube Theory
For the stationary stream tube theory it results that the fluid elements
appertaining to a stream filament appertain to this stream filament permanently.
Fluid particles that are located outside a stream filament at a certain point in
time, can never become components
of
the considered filament. Each fluid
particle
of
a stationary flow area belongs to a certain stream filament though,
so that it
is
possible to describe the properties
of
the flow area by the properties
of
the considered stream filaments.
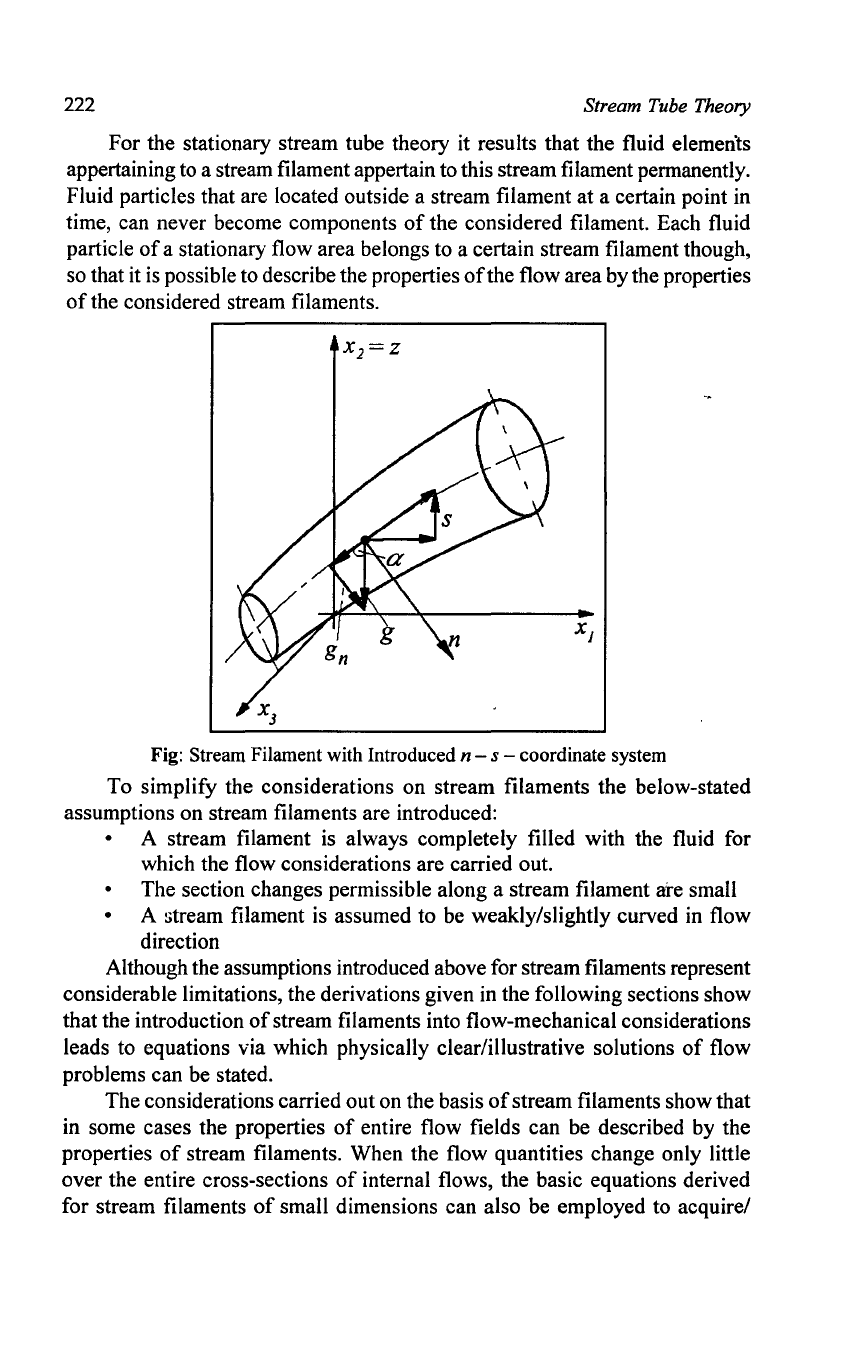
Fig: Stream Filament with Introduced n - s - coordinate system
To simplify the considerations on stream filaments the below-stated
assumptions on stream filaments are introduced:
• A stream filament is always completely filled with the fluid for
which the flow considerations are carried out.
• The section changes permissible along a stream filament are small
• A gtream filament is assumed to be weakly/slightly curved in flow
direction
Although the assumptions introduced above for stream filaments represent
considerable limitations, the derivations given in the following sections show
that the introduction
of
stream filaments into flow-mechanical considerations
leads to equations via which physically clear/illustrative solutions
of
flow
problems can be stated.
The considerations carried out on the basis
of
stream filaments show that
in some cases the properties
of
entire flow fields can be described by the
properties
of
stream filaments. When the flow quantities change only little
over the entire cross-sections
of
internal flows, the basic equations derived
for stream filaments
of
small dimensions can also be employed to acquire/

Stream Tube Theory
223
record the most important properties
of
internal flows by a one-dimensional
flow theory. To this purpose the internal flow is treated as a single stream
pipe.
The justification for this is given only, however, when friction influences
are small or can be neglected for first considerations
of
flows.
DERIVATIONS
OF
THE
BASIC
EQUATIONS
Continuity
Equation
The derivation
of
the continuity equation for a stream filament builds up
on the differential form
of
mass conservation and which, after integration over
a control volume, having employed Gauss' integral theorem:
ap
+
a(pu;)
= 0
'V'T
S(a
p
)
dV + S pU;dFj = 0
at
ax
j v
at
0
c c
Here
Vc
is equal to the volume
of
the considered control volume and
Oc
is its surface. Exchanging in the first term
of
the above equation integration
and differentiation, one obtains:
.§...
SpdV + SpU.dF..
=0
'V'T
aMc
=-
SpU.dF..
at
I I
at
I I
Vc
Oc
Oc
Applying the form
of
mass conservation to a stream filament and
considering that the flow passes only through the cross-sectional areas
of
the
. aM
stream filament, for
at
c = 0 (stationary flow conditions) it results that the
mass inflows and outflows for a stream filament are the same.
S
pUjdj
j
= S
pUjdj
j
'V'T
FAUs,APA
=
FBUs,BpB
FA FB
where the plane
of
the area F stands vertically to the flow direction s
Therefore it results that the mass flow
Til
= pF
Us
along a stream filament
is
constant.
In the considerations carried out above it was already said that because
of
small cross-sectional stream filaments F, p and
Us
can be set equally constant
over
F When one wants to apply the considerations also to stream pipes, the
considerations have to be carried out
in
a refined/improved way.They have to
consider that the assumption
of
constant density and velocity
in
the presence
of
large cross-sectional areas is only given conditionally. The introduction
of
cross-sectionally averaged quantities into the considerations carried out is
necessary as has been shown below.
When carrying out the following averaging, with employment
of
the
meanvalue theorem:

224
Stream Tube Theory
Stream
Tube
Theory
n
n
F(s)
Rohrstromung
Diisenstr0lpung
Fig. Flows which can be Computed
One-Dimensionally
by
the Approximation Method
pUs =
__
1 f pUsdfs
Fs
F:
a
it can be stated for stationary flow considerations :
=0
~
aM
c = _ f pUjdFj
-v-+
(pUS)A
FA
= (PiJ;)B
FB
at
v
c
This relation for the mass flows
is
often simplified further in stream-tube
theory by assuming
Pu; =
pUs
i.e. the relation is employed as follows:
PAUs,AFA
=
PBUs,BFB
= pUsFs
where
PA
and PB' as well as
Us,A
and
Us,B
are defined as follows:
The above derivations make clear that the employment
of
the simplified
integral form
of
the continuity equation
pUs~
= const is only justified for
such flows that have no strong variation in density or velocity over the flow
cross-section
of
a stream pipe. Equation finds employment in the following
sections on this assumption. As now strong variations
of
the quantities p and
U
l
over the cross section are excluded, it is also justified to introduce local
quantities in the above relation mechanics a number
of
questions arise that

Stream Tube Theory
225
aim at recording infinitesimal changes
of
a thermodynamic state
or
flow
quantity when infinitesimal changes
of
other parameters exist/take place/are
present. By differentiation
of
equation one obtains:
The division
of
equation leads to a further form
of
the continuity equation
which
is
employed in the following sections:
diS
+
drYs
+ dG = 0
is
Us
F
The equation expresses how e.g. the velocity
of
a fluid will change
relatively, when common relative changes in density and cross-section area
occur.
MomeRtum
Equation
Solutions
of
flow problems on the basis
of
the stream-tube theory requires
the inclusion ofthe momentum equations, however, these have to
be
transcribed
to the stream-filament coordinates. Starting from the general momentum
equations
[
aU
j
aUj
1 ap
mij
p
--+U;--
=-----+pgj
at ax;
ax
j ax;
and neglecting the molecular momentum-transport terms for the s-direction
of
the stream filament, the following form
of
the momentum equations results:
[
aU
au]
ap
.
p
a/
+U
s
ax:
=-a;+pgs
mltg
s
=-gcosa.
az
with cos
a.
=
as
' so that it holds:
p[au
s
+U
s
au
s
]
= _ ap
_pg
dz
at
as
as
ds
In an analogous way it can be stated in n - direction
U;
ap
dz
p-=---g-
R
an
dn
where z in
is
to be chosen in the negative direction
of
the gravitational
field. This equation expresses that for straight, non-curved stream filaments,
i.e
R
~
00
the pressure variation vertical to the flow direction is given only by
the gravitation. When the gravitational forces are negligible, the pressure over
the cross-section
of
a non-curved stream filament is constant.
Stream Tube Theory
Starting from the general momentum equation in
Euler's
form, i.e.
neglecting the molecular momentum-loss terms
226
Stream Tube Theory
a(pu
j)
a(puju
j )
ap
--'--~+
---+pg'
at ax; ax j J
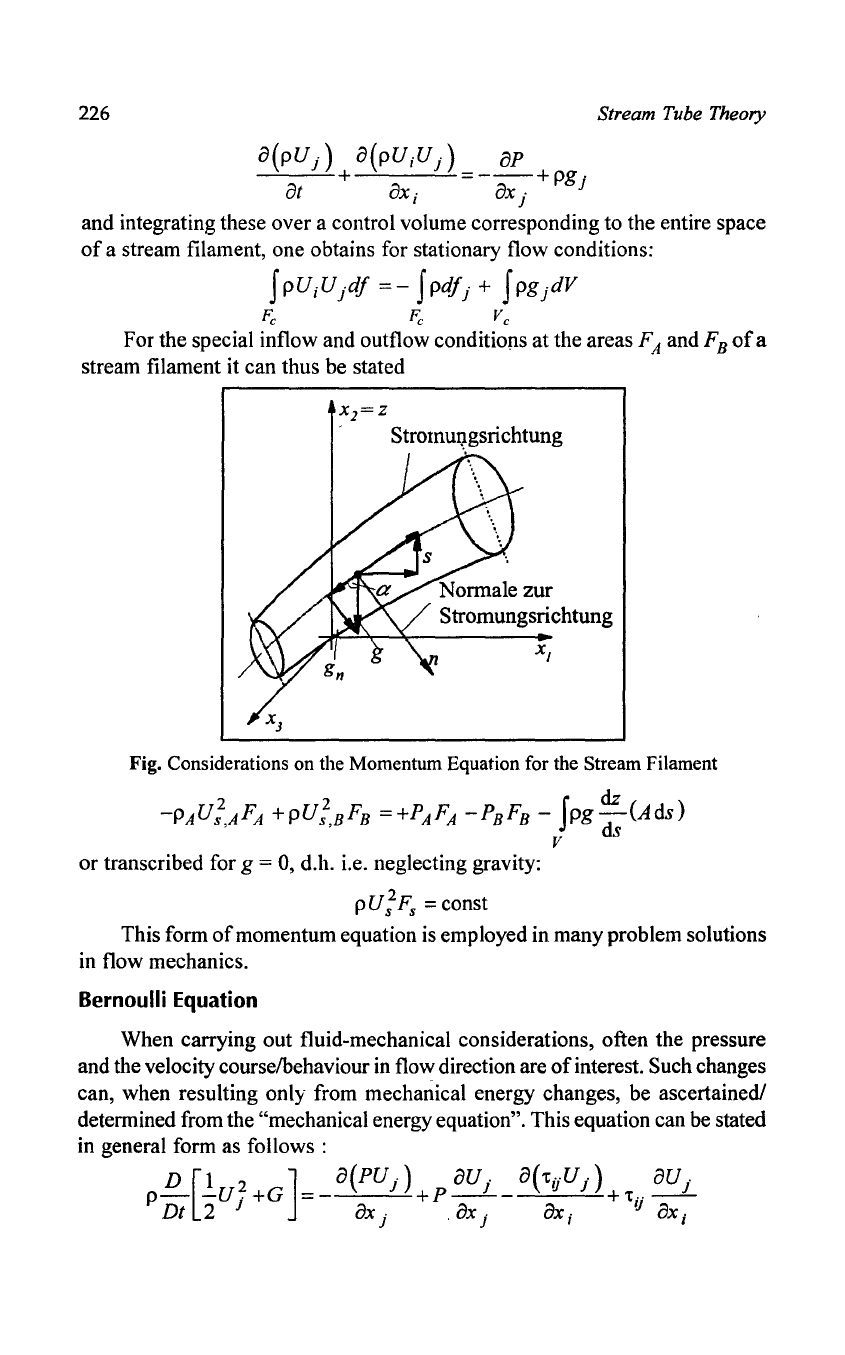
and integrating these over a control volume corresponding to the entire space
of
a stream filament, one obtains for stationary flow conditions:
J
pUjUjdf
=-
J
pdfj
+ J
pgjdV
Fe Fe
Ve
For the special inflow and outflow conditioflS at the areas
FA
and
FB
of
a
stream filament it can thus be stated
x]=z
,
Stromu~gsrichtung
Nonnale
zur
Stromungsrichtung
Fig. Considerations on the Momentum Equation for the Stream Filament
-PAul
AFA
+pu;
BFB
=+PAF
A
-PBF
B
-
Jpg
dz (Ads)
" ds
V
or transcribed for g = 0, d.h. i.e. neglecting gravity:
p
U;
Fs
= const
This fonn
of
momentum equation
is
employed in many problem solutions
in flow mechanics.
Bernoulli
Equation
When carrying out fluid-mechanical considerations, often the pressure
and the velocity courselbehaviour
in
flow direction are
of
interest. Such changes
can, when resulting only from mechanical energy changes, be ascertained!
determined from the
"mechanical energy equation". This equation can be stated
in general form as
follows:
D
[1
2 ]
a(pu
j
)
aUj
a
('tY'U
f
)
aUf
p-
-U·
+G
=-
+P---
+'t
..
--
Dt
2 J ax j . ax j ax j
IJ
ax i

Stream Tube Theory
227
When carrying out considerations neglecting the molecular-dependent mo-
mentum -transport terms, i.e. for
'tij
= 0, then one obtains for p = const and
au·
__
J =0
thus
Oxj
p~[!uJ+G]=_a(PUj)
-U.
ap
Dt 2
ax
j J
ax
J
In the presence
of
stationary pressure fields it holds:
DP = ap +U.
ap
=U.
ap
Dt
.§!..
I
ax
i I
ax
i
=0
so
that
under these conditions it holds:
p~[!U?
+GJ
= _ DP
Dt 2 J Dt
For G =
-Xj
~ thus can be written:
p~[!U2
+ P
-x.g
.]=0
Dt 2 J P J J
which leads for j =
s.
to the statement
of
the Bernoulli equation:
!U
2
+ P
_g
s
=const
2 s p s
Considering that
-g~
= gh one obtains the final form
1
2 P
-Us
+-+gh
=const
2 p
This equation can be interpreted physically such that the mass m, flowing
into a stream filament
per
time unit, introduces the kinetic energy
liz
±U;
,
'P
. P
the
pressure energy m u = m - and the potential energy MJgh as total
- p
energy, whose sum along the stream filament cannot change, i.e. the total
energy is constant along the stream filament. As at the same time m = const.
holds, equation results from this.
The
Total
Energy
Equation
The above considerations on the Bernoulli equation must experience
expansion/extension when carrying out energy considerations for compressible
media. The equation for the total energy has to be employed instead
of
the
above-treated mechanical energy equation. According to equation it can be
stated as follows:

228
Stream Tube Theory
pE-[e
+!U~
+GJ=-
arjj
_
a(pu
j
) _
('CijU
j
)
Dt 2 ] ax i ax j
xi
Neglecting the molecular-dependent heat and momentum transport, i.e
q i = 0 and
'tij
=
O,it
results for g
""
0:
~[pe+!pu~J+~[u.
+!Pu~J=~(PU.)
at
2 ]
ax
. I 2 ]
ax
. ]
I ]
For stationary flow processes then holds:
~[pe
+!Pu~J+~[u.
(pe
+!PU~)]
=~(PU.)
ax.
2 ]
ax·
I 2 ]
ax·
]
I I ]
Introducing the enthalpy h = e + P /p one obtains compressible media for
the energy equation for stationary flows:
(h
+~uJ
)=const
When carrying out the above considerations for stream pipes, one obtains
also the relation stated in equation, for area-averaged quantities though:
ii
+!UJ~
=const
2 .
The sum from the area-averaged enthalpy
of
a flowing fluid and the
areaaveraged kinetic energy available per kg
of
the fluid is a constant for
adiabatic flows free from viscosity in stream pipes, when gravity influences
are negligible. With this the following equations for the computation
of
flows
in stream pipes result.
Flows
of
incompressible fluids:
•
Mass conservation:
p~Us
=const
•
Momentum conservation:
pU;Fs
+PF
s
=const
•
{
I
-2
P -}
Mechanical energy equation:
""iUs
+ p + gh =const
Flows
of
compressible fluids:
•
Mass conservation:
p~Us
=const
•
Momentum conservation:
PsU;Fs
+PF
s
=const
. 1
-2
-
Energy equatIOn:
""iUs
+ h = const
•
Stream Tube Theory
229
INCOMPRESSIBLE
FLOWS
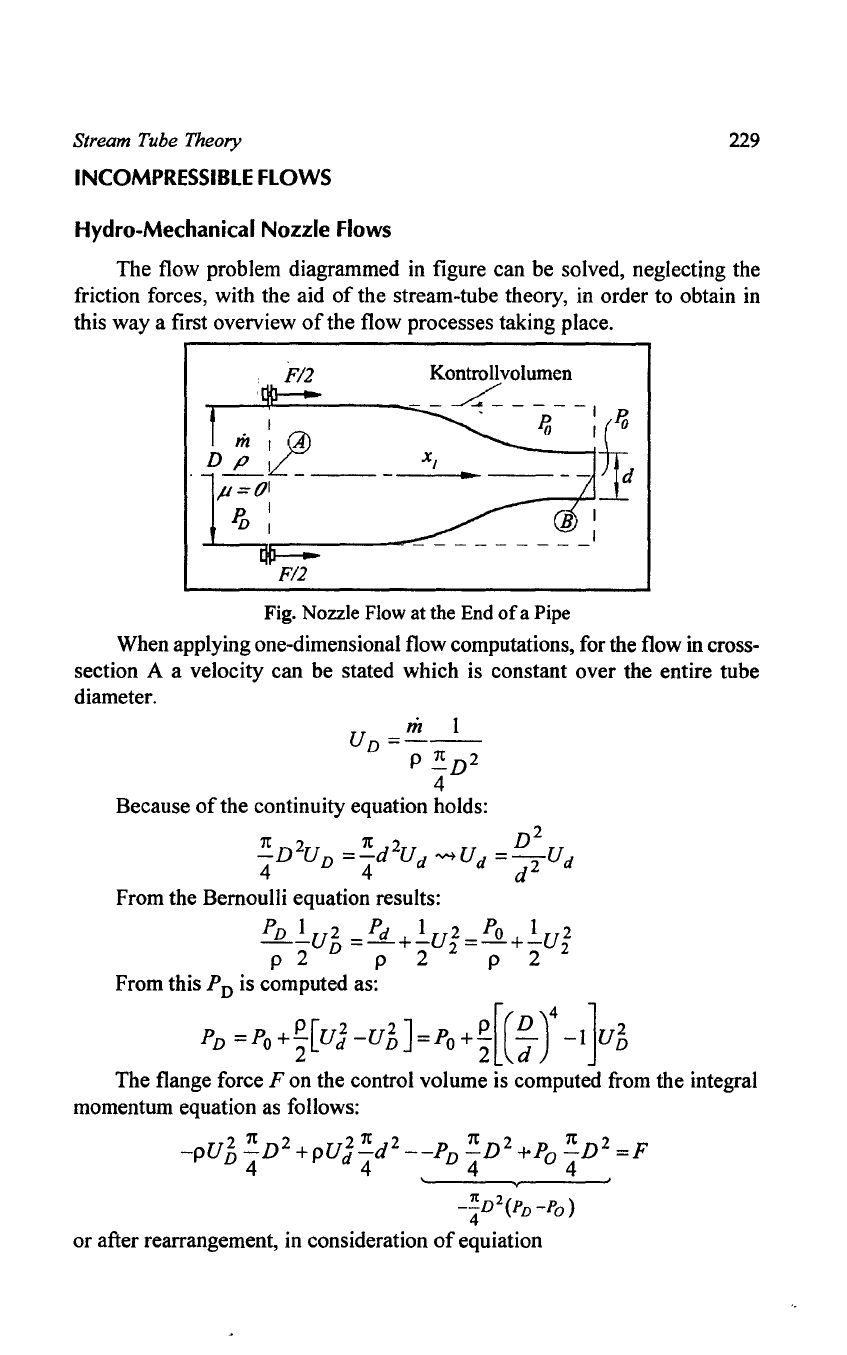
Hydro-Mechanical Nozzle Flows
The flow problem diagrammed in figure can be solved, neglecting the
friction forces, with the aid
of
the stream-tube theory, in order to obtain in
this way a first overview
of
the flow processes taking place.
D;
~
__
_
p=(}1
E I
D I
-'--06=;:.------
- - - - - - - -
FI2
Fig. Nozzle Flow
at
the End
of
a Pipe
When applying one-dimensional flow computations, for the flow in cross-
section A a velocity can be stated which is constant over the entire tube
diameter.
m 1
U
D
=---
P
~D2
4
Because
of
the continuity equation holds:
1t 2 1t 2
D2
-D
U
D
=-d
U
d
-U
d
=-U
d
4 4 d
2
From the Bernoulli equation results:
P
D
~u'i
= P
d
+~ui
=
Po
+~ui
p 2 p 2 p 2
From this P D is computed as:
PD
=Po+~[UJ
-u~J=Po+i[(~
r
-l]U~
The flange force F on the control volume is computed from the integral
momentum equation as follows:
-pu'A
1tD2+pU]
1t
d
2
__
PD!!..D2+PO
1t
D
2=F
4 4 4 4
\ v I
-'!!..D
2
(P
D
-po)
4
or after rearrangement, in consideration
of
equiation
230
Stream Tube Theory
[
2
2]
[ 2 1
p 1t 2 2 d U
d
1t 2 P D 2
---D
U
D
2-2--
--D
-
--1
U
D
=F
24
D2
U};
4 2 d
4
and after further rearrangement
P 1t 2 2 [
D2]2
-Z4
D
U
D
1-
d
2
=F
When inserting the corresponding relations U
D
'
one obtains for the flange
force
F:
F =
,;,2
[1-
D2]2
1t 2 d
2
P2
D
DThe force applied by the flange on the examined nozzle part proves to
be positive, so that the supporting surface
of
the flange is pressurized with a
negative force
F The screws in the flange can therefore be regarded to be
force-free.
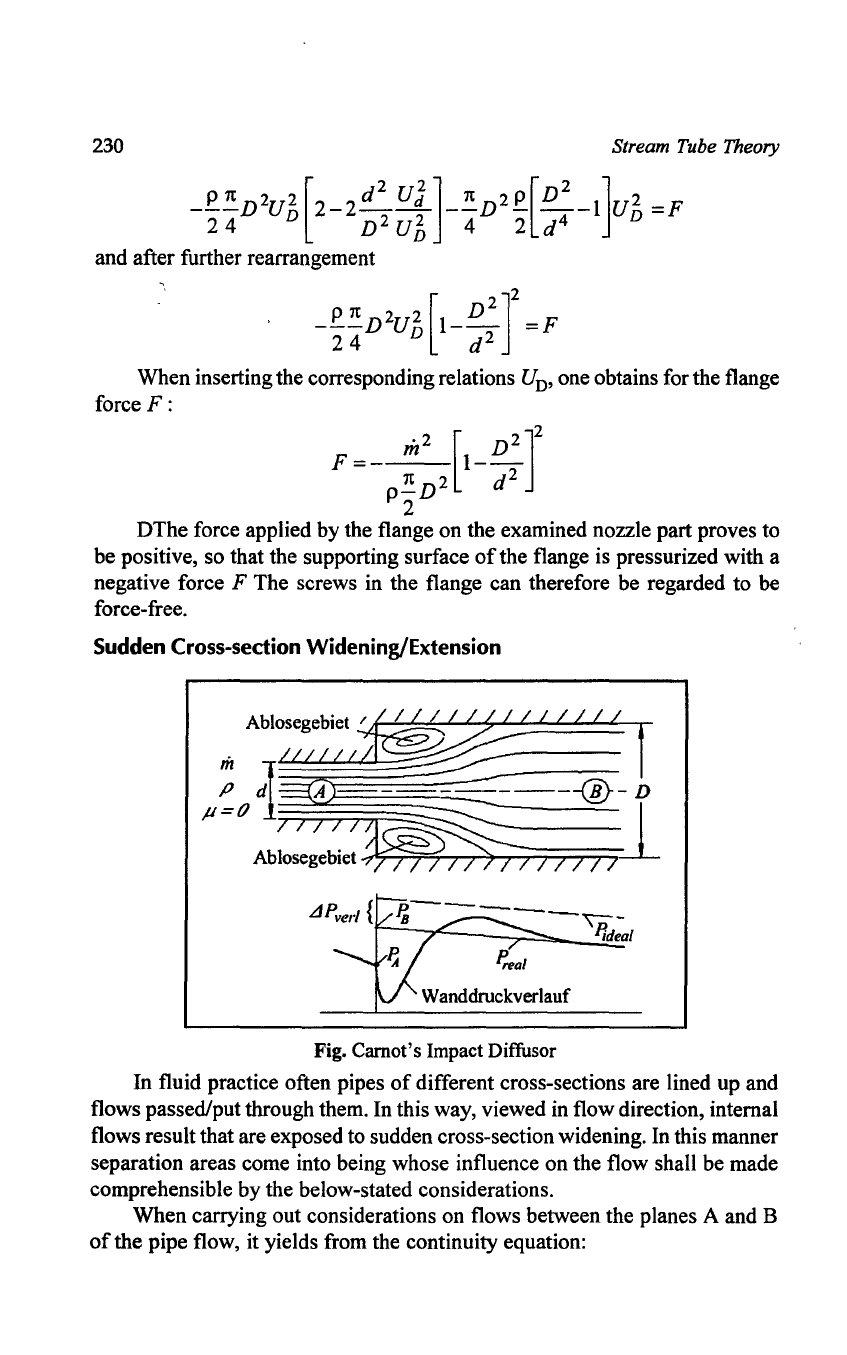
Sudden Cross-section Widening/Extension
AblOSegebiet~
/ / / / / / /
P~o1I1ifE--~1
Ablosegebiet
Jj~;;S
7 I I 7 7
II
Fig. Carnot's
Impact
DitTusor
In
fluid practice often pipes
of
different cross-sections are lined up and
flows passed/put through them. In this way, viewed in flow direction, internal
flows result that are exposed to sudden cross-section widening. In this manner
separation areas come into being whose influence on the flow shall be made
comprehensible by the below-stated considerations.
When carrying out considerations on flows between the planes A and B
of
the pipe flow, it yields from the continuity equation:

Stream Tube Theory
231
m
1t2
1t2
-=Ud-d
=UD-D
P 4 4
Thus the velocities U
d
and U
D
are known, they are determined by the
given mass flow.
In the case
of
flows passing through the measuring length without losses,
the following difference in pressure
wdnld result between A and B which can
be computed from the Bernoulli equation!'
P
2[
d
4
]
M'ideal
=(P
B
-P
A
)ideal
=2
Ud
1-
D4
Under real conditions, by the occurrence
of
the separation areas.
F
=pUJ
1t
-pUb
1t
D
2
+P
A
::"d
2
-P
B
1t
D
2
4 4 4 4
When one neglects the contributions to the force F by momentum losses
at the pipe walls, then the force
F.
is computed as the pressure force on the
ring surface after the sudden widening, i.e. as
F
=P
A
1t(D2
=d
2
)
4
Thus one obtains for the pressure difference
2 d
2
(
d
2
)
DP
real
=(P
A
-P
B
)real
=pU
d
D2
1-
D2
'
so that a pressure loss (Carnot's impact loss) can be determined as follows:
p
2(
d
4
)
P(
2
2)
M'Veri.
-M'ideal'=
M'real.
=2Ud
1-
D4
=2
U
d
-U
D
For D
~
00
results as a maximum value for
L1P
Veri.
::= £.U
J,
the discharge
2
pressure loss.
INCOMPRESSIBLE
FLOWS
Influence
of Area
Changes
on
Flows
In the present section general considerations shall be carried out which
give information on what effect cross-section changes in flow channels have
on fluid flows, i.e. to what extent area changes determine the distribution
of
velocity, pressure,
density
and
temperature
along
the channel. In
the
investigation the equations are employed, the continuity equation reads:
pU1F
=oonst
Equation can be written in differential form:
