Brewster H.D. Fluid Mechanics

252

Potential Flows

complex number plane. Inversely it can be said that for each analytical function

holds that its real part represents automatically the potential

of

a flow field

whose flow lines are described by the imaginary part

of

the complex function.

As a consequence it results that each real part

of

an analytical function and

also the imaginary part, each for itself, fulfil the two-dimensional Laplace

equation. Analytical functions as they are dealt with in function theory can

thus be employed for describing potential flows. When setting their real part

9{

(x,

y) equal to the potential function

(x,

y)

andJhe

imaginary part Im(x,

y)

equal to the stream function

'I'

(x,

y), it is possible to state the equipotential

and the flow lines.

By

proceeding in this way solutions to flow problems are

\ obtained without partial differential equations having to be solved. The inverse

way

of

proceeding that is thus sought here for the solution

of

flow problems,

namely interpreting a known solution

of

the potential equation as a flow is

regarded as acceptable because

of

the evident advantages

of

proceeding like

this.

From a complex potential

F (z) a complex velocity can be derived by

differentiation.

As

F (z) represents an analytical function, thus is steady and

steadily derivable, the derivation has to be independent

of

the direction in

which

it

is determined, as is shown in the following.

As

because

of

the

steadiness

of

F (z) holds

dF

= lim M = lim M

dz

&~O

&

&~o(z

+&

)-z

1

.

M

=

1m

&~O(X

+Llx

)+i

(y

+~y

)-(x

+iy)

and as one is free

to

choose the

way

on

which & goes towards zero (the

derivation has

to

be independent

of

the selected way), the following special

ways can also

be

taken into consideration:

~y

= 0:

dF

= lim M = lim M =

aF

dz

6x

.....

0 (x +

Llx

) + iy - (x + iy )

6x

.....

0

Llx

ax

Llx

=0:

dF

= lim M

dz

6y

.....

OX

+i

(y

+~y

)-(x

+iy)

. M

aF

.oF

=

hm

--=--=-1-

6y

.....

0 i

~y

i

8y 8y

The derivation

of

the complex potential F(z) thus reads for x =

Xl:

w

(z

) =

dF

(z

)

8

+ i

a'l'

dz

aXI

ax

l

or

expressed in velocity components:

w

(z)

=U

I

-iU

2

.

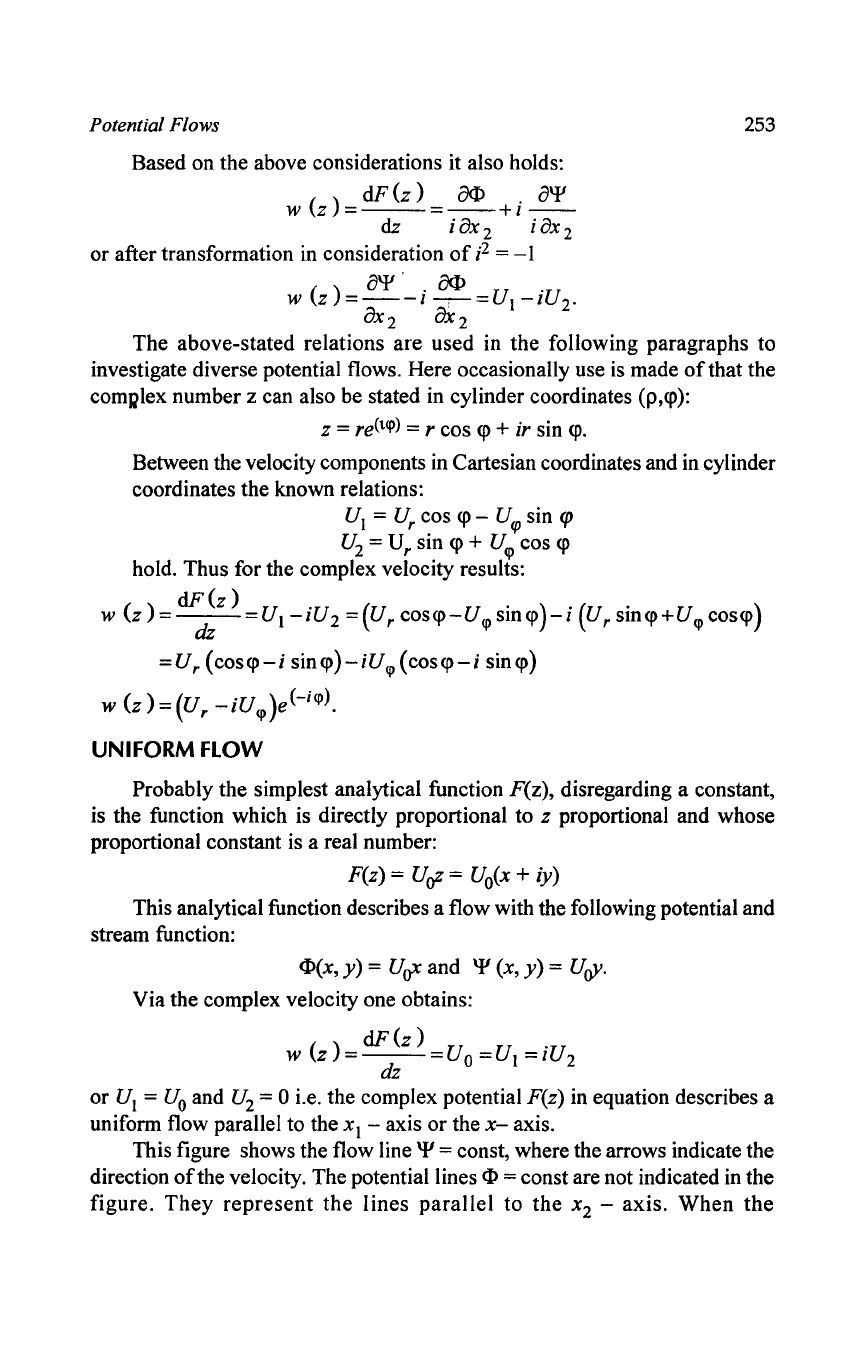
Potential Flows

Based on the above considerations it also holds:

w (z ) = dF (z ) =

8<1>

+ i 8'I'

dz

i8x2

or after transformation in consideration

of

P =

-1

w (z ) = 8'I'

'-i

8<1>

=U

I

-iU

2

.

8x2

8x

2

253

The above-stated relations are used in the following paragraphs to

investigate diverse potential flows. Here occasionally use

is

made

of

that the

coml2lex number z can also be stated in cylinder coordinates (p,q»:

z =

re(tcp)

= r cos

q>

+

ir

sin

q>.

Between the velocity components in Cartesian coordinates and in cylinder

coordinates the known relations:

U

I

= U

r

cos

q>

-

UqJ

sin

qJ

U

2

= U

r

sin

q>

+

Ulp

cos

q>

hold. Thus for the complex velocity results:

w (z ) =

dF

~z)

U

I

-iU

2 =

(U

r

cosq>-U

cp

sinq>

)-i

(U

r

sinq>+U

cp

cosq»

=U

r

(cosq>-i sinq»-iUIp(cosq>-i

sinq»

W (z

)=(U

r

-iUIp)e<-ilp).

UNIFORM FLOW

Probably the simplest analytical function F(z), disregarding a constant,

is the function which is directly proportional to

z proportional and whose

proportional constant is a real number:

F(z) =

Urf

= Uo(x + iy)

This analytical function describes a flow with the following potential and

stream function:

cI>(x,

y)

=

UoX

and

'I'

(x,

y)

= Ur}'.

Via the complex velocity one obtains:

)

dF(z)

.

W

(z

=

=U

o

=U

I

=zU

2

dz

or

U

I

= U

o

and U

2

= 0 i.e. the complex potential F(z) in equation describes a

uniform flow parallel to the

Xl

- axis

or

the

x-

axis.

This figure shows the flow line

'I'

= const, where the arrows indicate the

direction

of

the velocity. The potential lines

cI>

= const are not indicated in the

figure.

They

represent

the

lines

parallel

to

the

x

2

-

axis.

When

the

254

proportionality constant is imaginary, i.e. it holds:

F (z) =

iV

<f

= Vo(-y + ix)

then one obtains for the potential and stream functions:

(x,

y) = -

VoY

and

'¥

(x,

y)

=

VoX

For the complex velocity it is computed:

w(z)

=

iVo

= VI

-liV

2

Potential Flows

or VI = 0 and V

2

= - V

o

.,

i.e. in this case the complex potential describes a

flow parallel to the

x

2

-

axis or the

y-

axis which takes place in the direction

of

the negative axis.

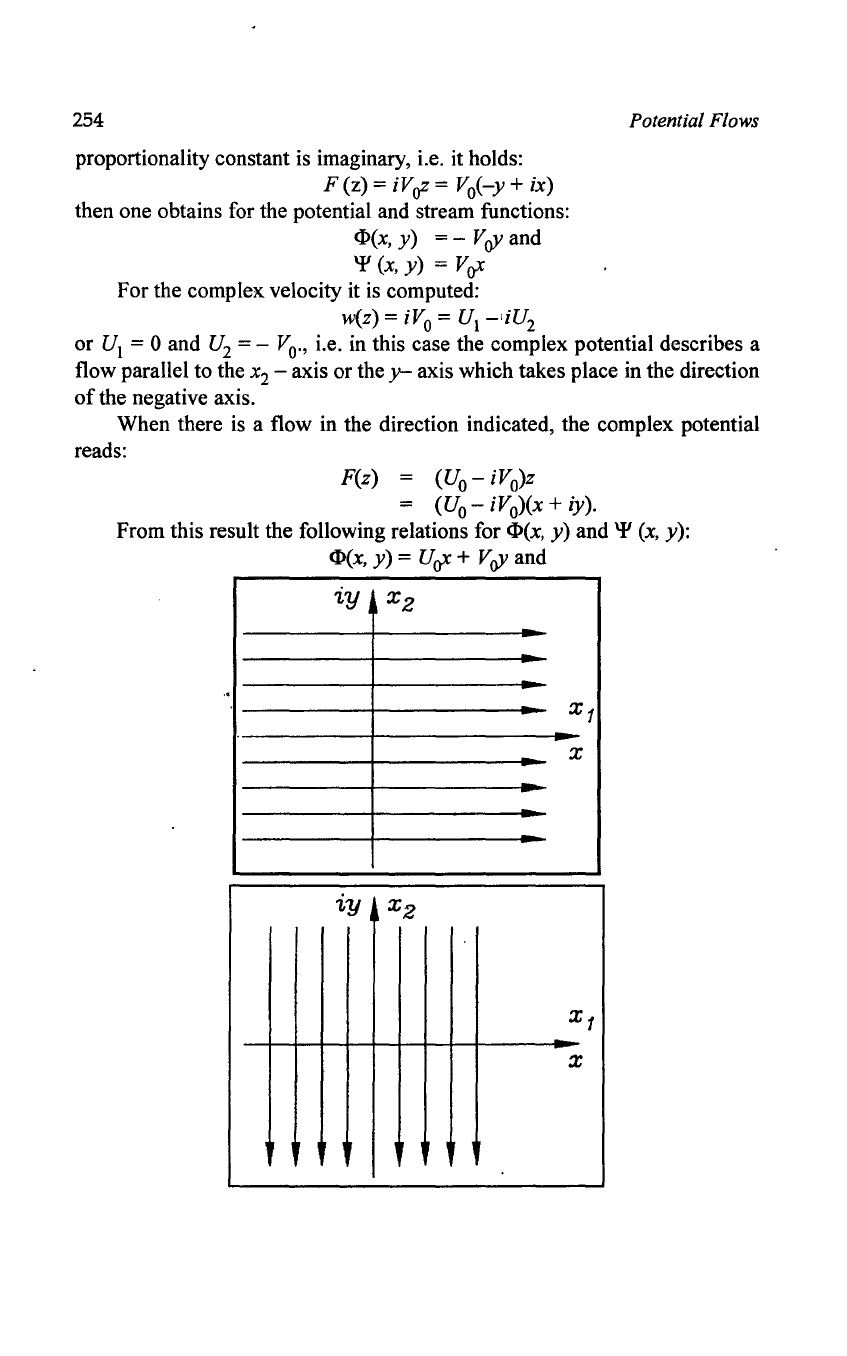
When there is a flow in the direction indicated, the complex potential

reads:

F(z) =

(Vo

-

iVo)z

= (Vo - iVo)(x + iy).

From this result the following relations for

(x,

y) and

'¥

(x,

y):

(x,

y) =

VoX

+

VoY

and

iy

x2

-,

x

t

x

~

iy

x2

x

t

X

Potential Flows

~,-~,-~~~,-~,-~~~X1

X

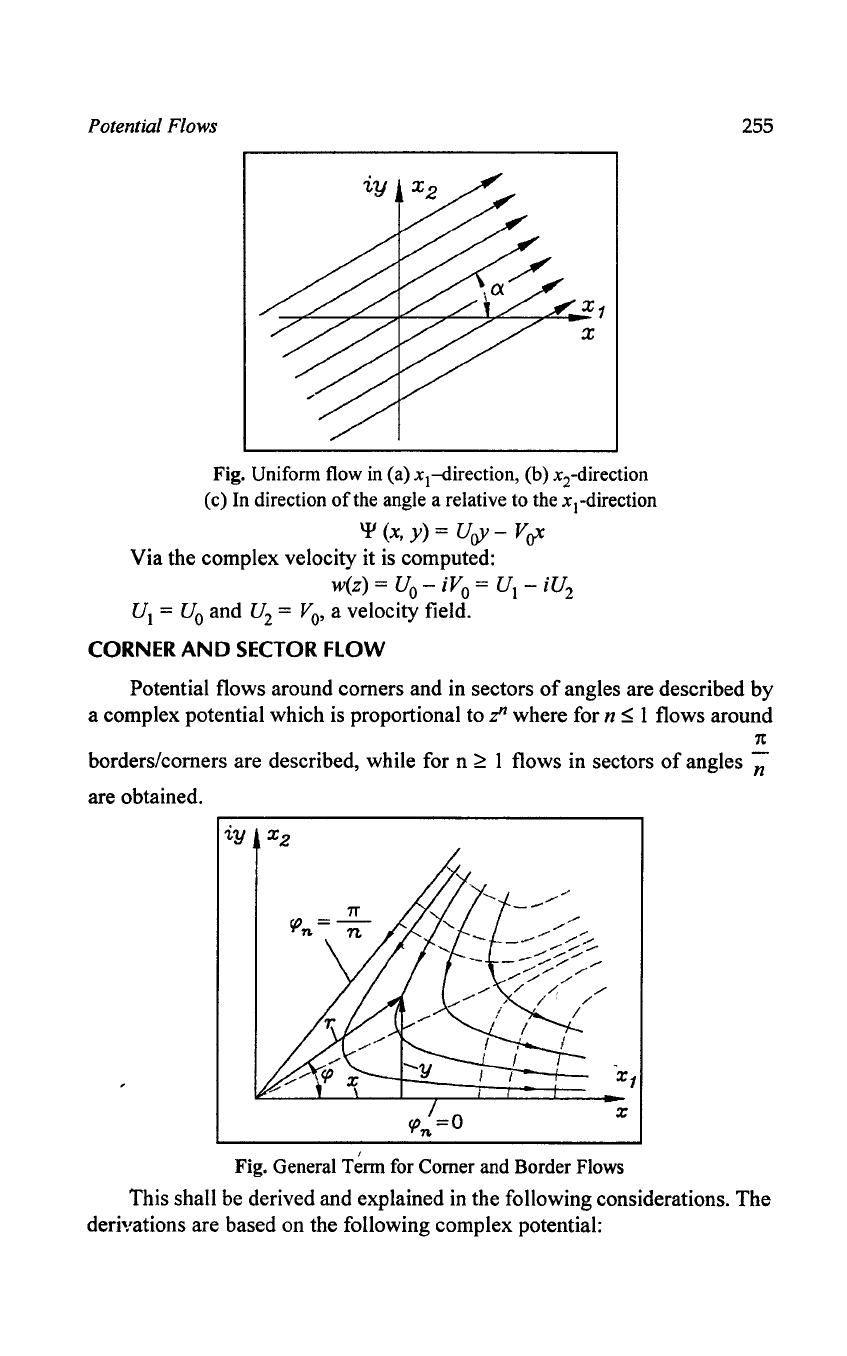
Fig. Unifonn flow in (a) xc-direction, (b) x

2

-direction

(c) In direction

of

the angle a relative to the xl-direction

'II

(x.

y)

=

Vr}!-

VoX

Via the complex velocity it

is

computed:

w(z) =

Vo

- iVo =

VI

-

iV

2

VI

=

Vo

and V

2

= V

o

'

a velocity field.

CORNER

AND

SECTOR

FLOW

255

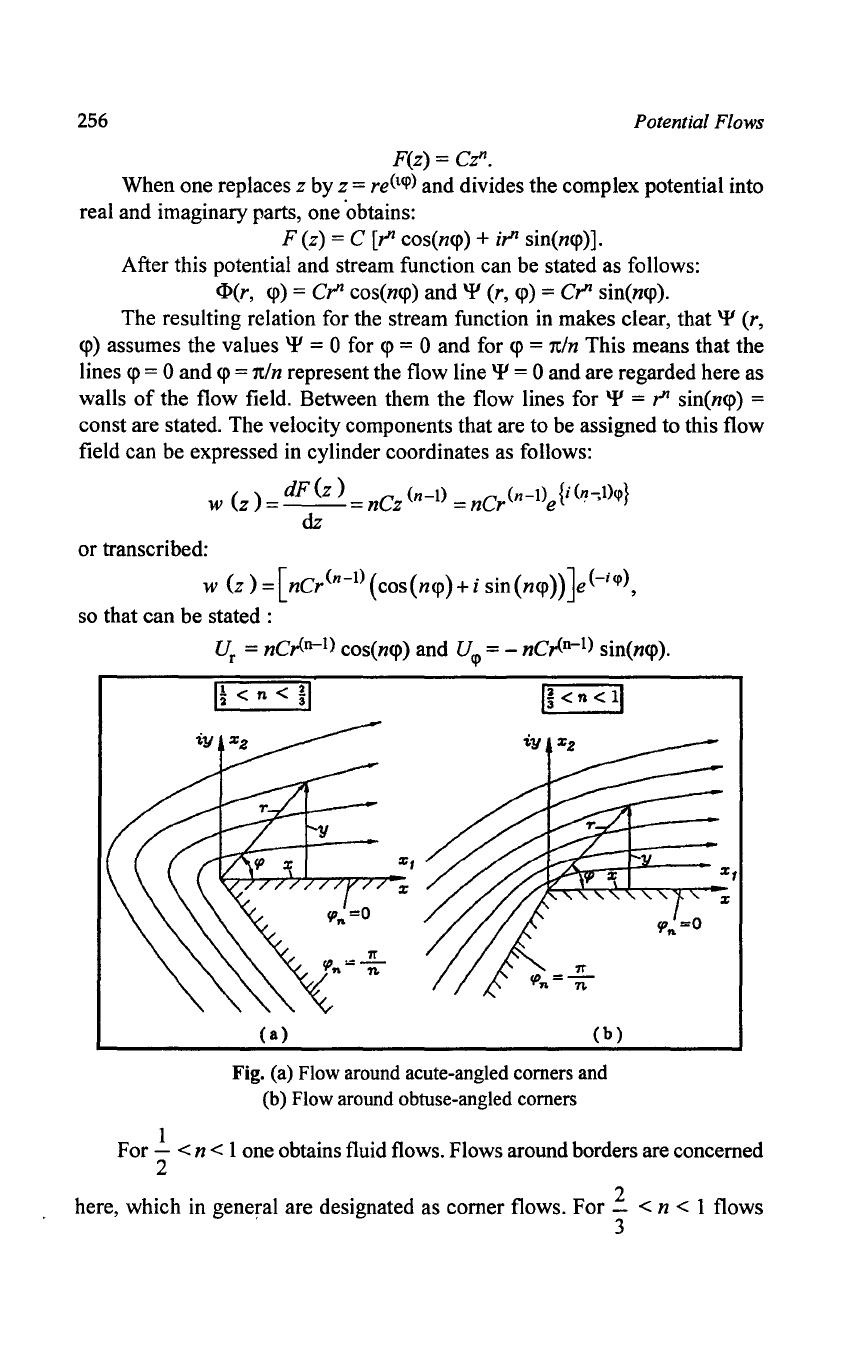
Potential flows around corners and in sectors

of

angles are described by

a complex potential which

is

proportional to z" where for n

$;

1 flows around

1t

borders/corners are described, while for n

~

I flows in sectors

of

angles -;;

are obtained.

({In

=0

x

Fig. General

T~nn

for Comer and Border Flows

This shall be derived and explained

in

the following considerations. The

derivations are based on the following complex potential:

256

Potential Flows

F(z) = Cz'l.

When one replaces z by z = re(up) and divides the complex potential into

real and imaginary parts, one ·obtains:

F (z) = C [r'l

cos(n<p)

+ ir'l

sin(n<p)].

After this potential and stream function can be stated as follows:

(r,

<p)

= Cr'l

cos(n<p)

and

'¥

(r,

<p)

= Cr'l

sin(n<p).

The resulting relation for the stream function in makes clear, that

'¥

(r,

<p)

assumes the values

'¥

= 0 for

<p

= 0 and for

<p

=

rein

This means that the

lines

<p

= 0 and

<p

=

rein

represent the flow line

'¥

= 0 and are regarded here as

walls

of

the flow field. Between them the flow lines for

'¥

= r'l

sin(n<p)

=

const are stated. The velocity components that are to be assigned to this flow

field can be expressed in cylinder coordinates as follows:

C

(n-l)

C

(n-l)

{i

(n-;l)cp}

n z

=n

r e '

or

transcribed:

w

(z

) = [

nC/n-l)

(cos(n<p) + i sin

(n<p»)

]e(-i

IP

),

so that can be stated :

U

r

= nCr<n-l)

cos(n<p)

and U

IP

= - nCr<n-l)

sin(n<p).

(a)

(b)

Fig. (a) Flow around acute-angled comers and

(b) Flow around obtuse-angled comers

For.!.

< n <

lone

obtains fluid flows. Flows around borders are concerned

2

here, which in general are designated as corner flows. For

~

< n < 1 flows

, 3

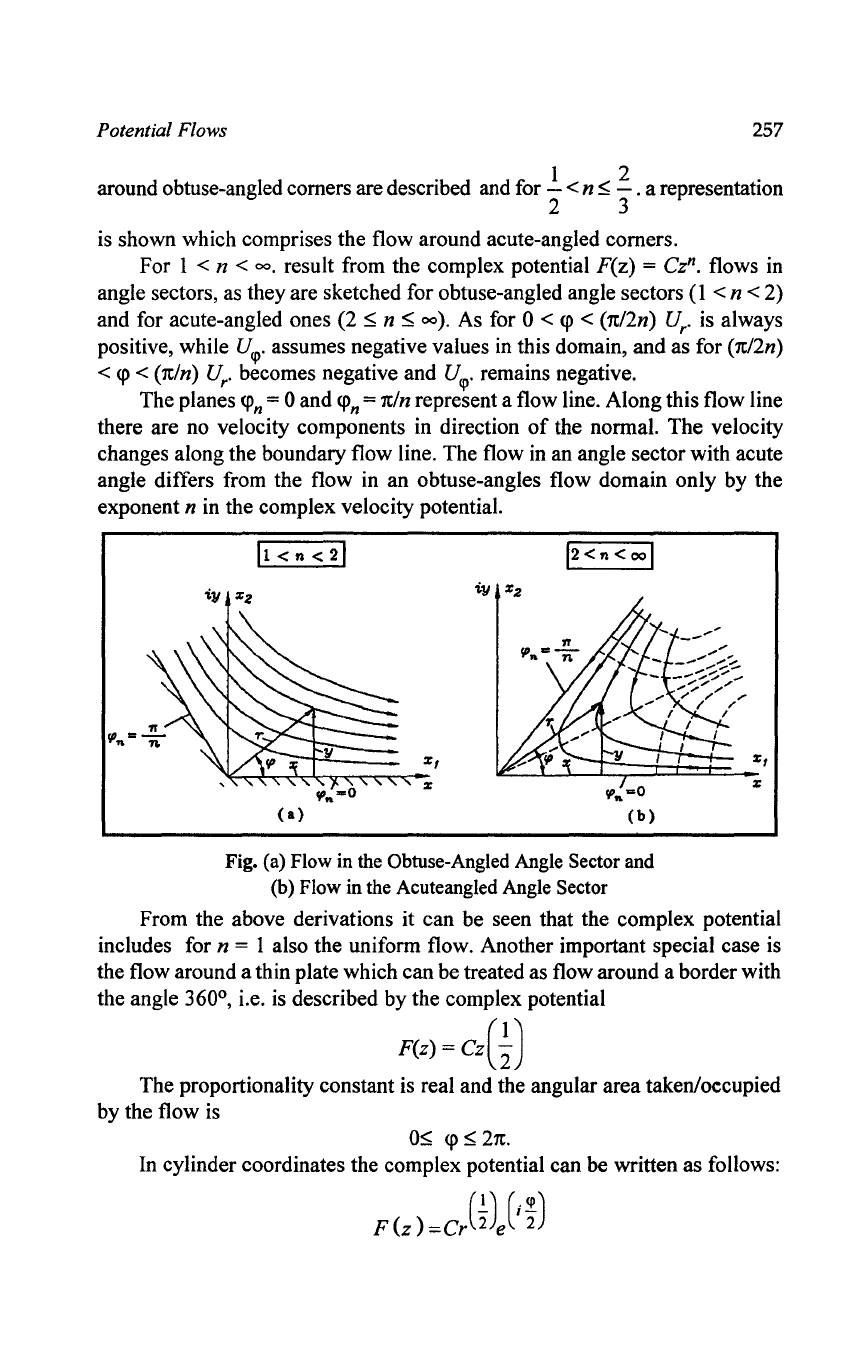
Potential Flows

257

around obtuse-angled comers are described and

for..!..

< n

~

. a representation

2 3

is shown which comprises the flow around acute-angled comers.

For 1

< n <

00.

result from the complex potential F(z) = Cz

n

.

flows

in

angle sectors, as they are sketched for obtuse-angled angle sectors

(1

< n < 2)

and for acute-angled ones (2

~

n

~

00).

As for 0 <

q>

< (1t/2n) U

r

•

is always

positive, while

Uf{>.

assumes negative values in this domain, and as for

(1t/2n)

<

q>

< (1tln) U

r

.

becomes negative and

Uf{>.

remains negative.

The planes

q>n

= 0 and

q>n

=

1tln

represent a flow line. Along this flow line

there are no velocity components in direction

of

the normal. The velocity

changes along the boundary flow line. The flow in an angle sector with acute

angle differs from the flow in an obtuse-angles flow domain only by the

exponent

n in the complex velocity potential.

%,

~~~~~~~~~%

<a>

iy

%2

(b)

Fig. (a) Flow in the Obtuse-Angled Angle Sector and

(b) Flow in the Acuteangled Angle Sector

From the above derivations it can be seen that the complex potential

includes for

n = 1 also the uniform flow. Another important special case

is

the flow around a thin plate which can be treated as flow around a border with

the angle

360°, i.e.

is

described by the complex potential

F(z) =

cz(~)

The proportionality constant is real and the angular area taken/occupied

by the flow is

O~

q>

~

21t.

In cylinder coordinates the complex potential can be written as follows:

258

Potential Flows

The potential and stream function can be stated as follows:

1 1

<t>(r,<p)=Cr

2

cos(~)

and

tJl(r,<p)=Cr

2

sin(~).

From the relation for the stream function can be derived that the lines

<p

= 0 and

<p

=

21t

correspond to the flow line

tJl

= 0 The flow lines for other

q>---

values are described by the stream function in equation. Also indicated are

the equipotential lines which are also computable. The complex flow velocity

is

conserved by derivation

of

the complex potential:

(

)

dF

(z)

C

w z =

=-(1)

dz _

2z

2

C

(-;!)

=--e

2

2r

G

)

or

transcribed:

w

(z

) =

C(~)

[cos (

~

) + i sin (

~

) } (-;

~)

.

2r

2

The velocity components thus are computed as follows:

C

(<PI

C .

(<p)

U r =

(~)

cos

"2)

and U

~

= -

(~)

sm

"2

.

2r

2

2r

2

iy.

Xl

Fig. Potential Flow Around the Border

of

an Infinitely Thin Plate

Potential Flows

259

These relations make it clear that the velocity component

Ucp

for 0 <

q>

<

21t

is negative, while U

r

for 0 <

q>

<

1t

is positive and for

1t

<

q>

<

21t

negative.

An important result

of

the above derivations it can be obtained that the

velocity field possesses a singularity in its origin. It is caused by the flow

around the plate border and characterized by extreme values

of

the velocity

field. The values

of

both velocity components approach the value r

~

0 for

00.

SOURCE

OR

SINK FLOWS

AND

POTENTIAL VORTEXES

When one chooses a complex potential F(z), which is proportional

to

the

natural logarithm

of

z., one obtains when selecting a real proportionality

constant and depending

on

whether one chooses a positive or negative sign,

the complex potential

of

a source

or

a sink flow:

F(z)

=

±C

In

z

or

with z = r .

e(icp)

F(z) = ±C [In r +

iq>]

=

<l>

+ i'P.

For

the potential and flow function one obtains thus:

<l>(r,q»=±C

In

r \jI(r,y)=±Cq>

<l>(x

,y

) = ±C

InJx

2 + Y 2 \jI(x

,y

) = ±C arctan

~

x

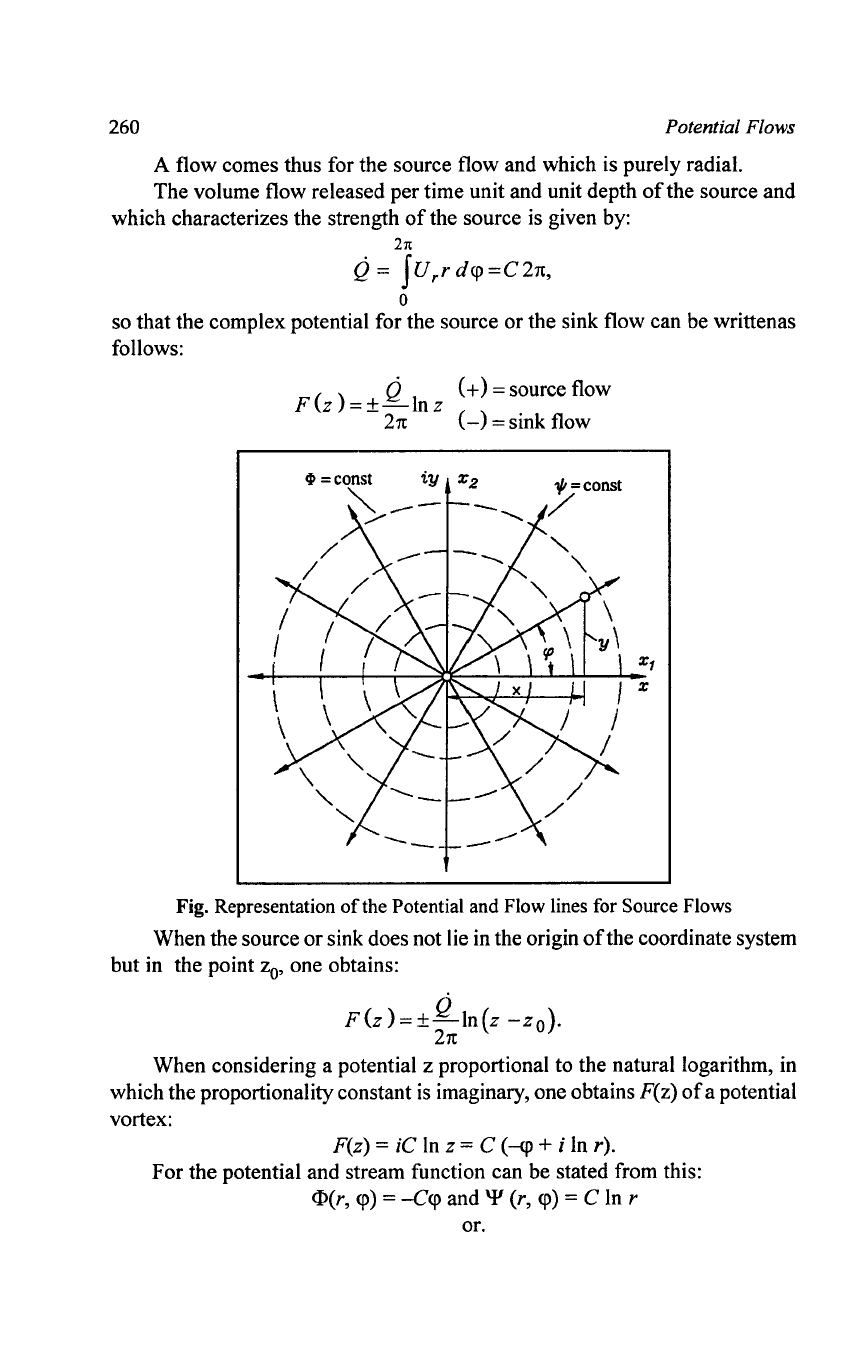
These equations show that the equipotential lines represent circles with r

= const while the flow lines represent radial lines with

q>

= const. When

computing the complex velocity:

w (z ) =

dF

(z

) = ±C

~

= ±C

(x

-

iy

) ,

dz z x

2

+y2

one obtains for the velocity components:

w

(z)=

2±C

2 (x

-iy

)=U

1

=-iU

2

x

+y

orU! =

~x

2 and U

2

=

~y

2.

x

+y

x

+y

In equation can also be written:

( )

±C

C (-iq»

W z

=-=±-e

z r

A comparison

of

equations shows that it holds:

C

U

r

=±-

and

Uq>

=0.

r

The velocity component U

r

decreases with lIr, has, however a singularity

in its origin

r =

O.

260

Potential Flows

A flow comes thus for the source flow and which is purely radial.

The volume flow released per time unit and unit depth

of

the source and

which characterizes the strength

of

the source is given by:

21t

Q =

fUrr

d<p

=C21t,

o

so that the complex potential for the source or the sink flow can be written as

follows:

Q (+ ) = source flow

F(z

)=±-Inz

21t

(-)

= sink flow

Fig. Representation

of

the Potential and Flow lines for Source Flows

When the source

or

sink does not lie in the origin

ofthe

coordinate system

but in the point zo' one obtains:

F(z

)=±

Q

In(z

-zo).

21t

When considering a potential z proportional to the natural logarithm, in

which the proportionality constant

is

imaginary, one obtains F(z)

of

a potential

vortex:

F(z) =

iC

In

z = C

(--<p

+ i

In

r).

For the potential and stream function can be stated from this:

(r,

<p)

=

-C<p

and

'¥

(r,

<p)

= C

In

r

or.

Potential Flows

<t>(z,y)

=-C'

arctan

L

and

\f(x,y)

=C

ln~x

2 + Y 2

X

261

These relations show that the equipotential radial lines represent

<p

= const

while the flow lines are circles with

r = const For the complex velocity can be

stated:

( )

_ dF

(z ) _

'C

1 _ . C (-;

<p)

w z - - I - - I

-e

.

dz z r

By comparing the equations, it results:

C

U

=0

and U

=--

r

<p

r

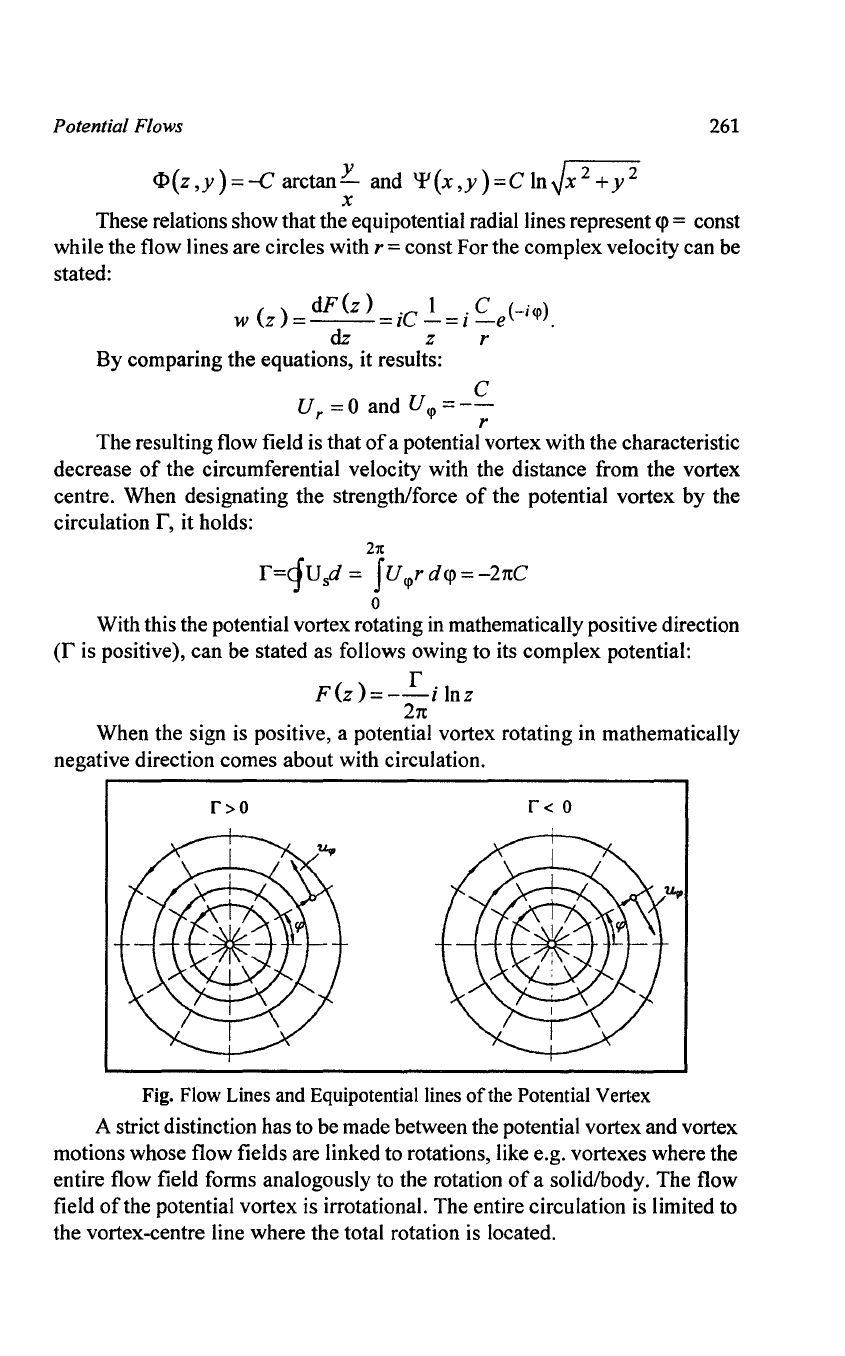
The resulting flow field is that

of

a potential vortex with the characteristic

decrease

of

the circumferential velocity with the distance from the vortex

centre. When designating the strength/force

of

the potential vortex by the

circulation

r,

it holds:

21t

r=4Usd

= JU<prd<p=-21tC

o

With this the potential vortex rotating

in

mathematically positive direction

(r

is positive), can be stated as follows owing to its complex potential:

F(z

)=-.i.-i

Inz

21t

When the sign is positive, a potential vortex rotating in mathematically

negative direction comes about with circulation.

r>o

r<

0

Fig. Flow Lines and Equipotential lines

of

the Potential Vertex

A strict distinction has to be made between the potential vortex and vortex

motions whose flow fields are linked to rotations, like e.g. vortexes where the

entire flow field forms analogously to the rotation

of

a solid/body. The flow

field

of

the potential vortex is irrotational. The entire circulation

is

limited to

the vortex-centre line where the total rotation is located.

Brewster H.D. Fluid Mechanics

Подождите немного. Документ загружается.