Brewster H.D. Fluid Mechanics
Подождите немного. Документ загружается.


232
Stream Tube Theory
dF + d P +
dq
1 = 0
F P U
1
The variation
of
the velocity in flow direction can be described in a first
approximation by Euler's equation, reduced for one-dimensional flows, i.e. it
holds:
PU
1
dU
1
=_
dP
=_
d~
dp
dx
1
dx
1
dp
dx
1
On the basis
of
the energy equation for reversible adiabatic fluid flows,
which for area-averaged quantities,
by way
of
approximation, holds as follows:
P
-=const
pX
the pressure diversion after the density is to be carried out under adiabatic
conditions. As it holds, however:
c
2
=(d~)
dp
ad
equation can also be written as follows:
-U-
dU
1
-2
dp
P
1--=-C
-
dx
1
dx
1
When one introduces the Mach number
Ma
of
the flow as:
M = U
1
IX
-
C
equation can be written:
dp
_ M 2
dU
l
-;--
IX
U
1
Inserting the result, we obtain:
dF
_M/
d
ql
+
dql
=0
F U
1
U
1
or
dU
1
1-
dF
U1 = (I-M/) F
When one takes into consideration that subsonic flows are given by
MIX
< 1 and supersonic flows by MIX> 1 the above relation expresses:
•
In
the presence
of
a subsonic flow (MIX < 1). a decrease
of
the
cross- sectional area
of
a flow channel in flow direction is linked to
an increase
of
the flow velocity. An increase
of
the channel cross-
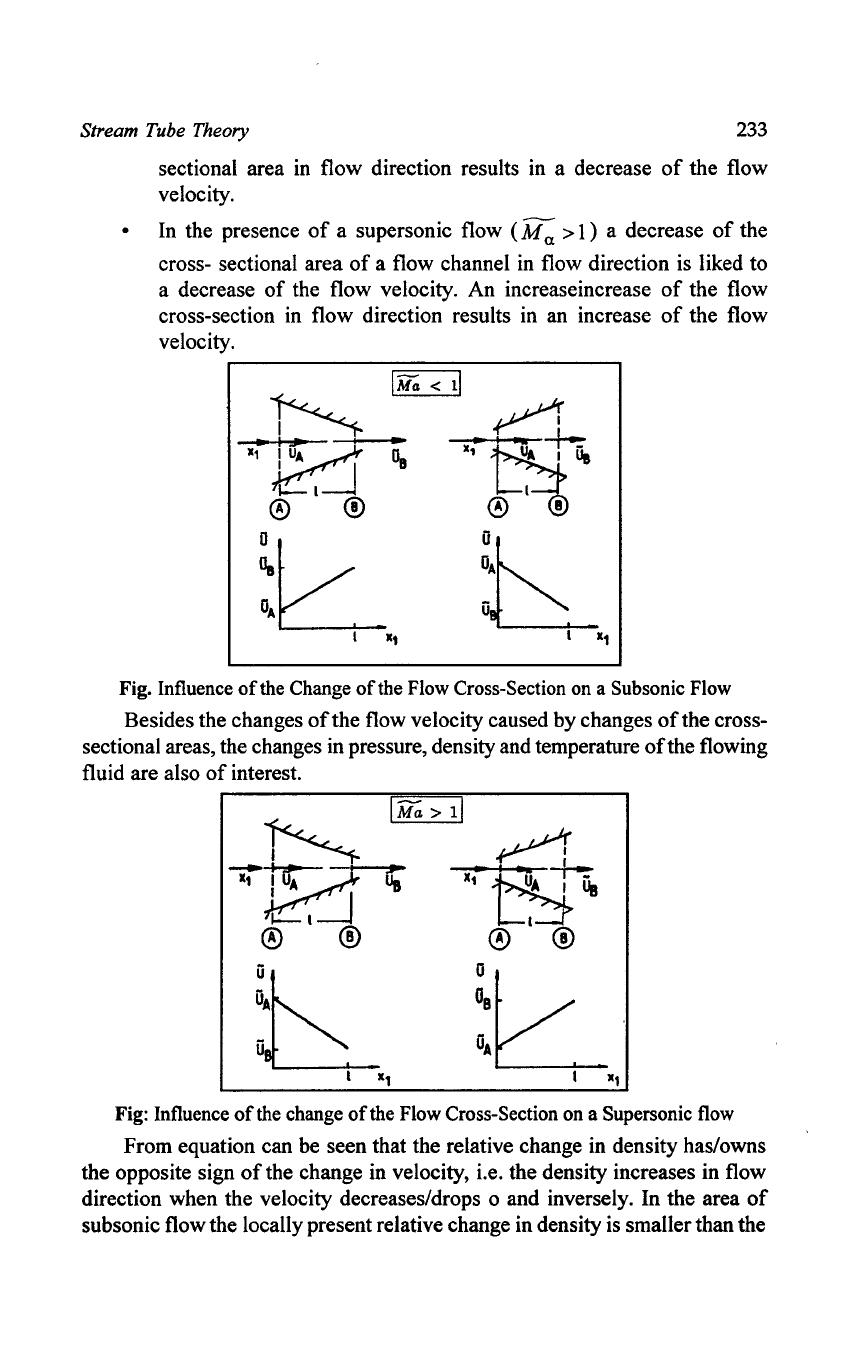
Stream Tube Theory
233
sectional area in flow direction results in a decrease
of
the flow
velocity.
• In the presence
of
a supersonic flow
(M
a > 1) a decrease
of
the
cross- sectional area
of
a flow channel
in
flow direction is liked to
a decrease
of
the flow velocity. An increase increase
of
the flow
cross-section in flow direction results in an increase
of
the flow
velocity.
Fig.
Influence
of
the
Change
of
the
Flow
Cross-Section
on
a Subsonic
Flow
Besides the changes
ofthe
flow velocity caused by changes
of
the cross-
sectional areas, the changes in pressure, density and temperature
of
the flowing
fluid are also
of
interest.
Fig:
Influence
of
the
change
of
the
Flow
Cross-Section
on
a Supersonic
flow
From equation can be seen that the relative change in density has/owns
the opposite sign
of
the change in velocity, i.e. the density increases in flow
direction when the velocity decreases/drops
0 and inversely. In the area
of
subsonic flow the locally present relative change in density is smaller than the

234
Stream Tube Theory
local relative change in velocity. In the area
of
supersonic flow the locally
present relative change in density is larger than the relative change in velocity.
As concerns the dependence from the cross- sectional area changes
of
the flow
channel, it results for the change in density:
dp
u:
2
elF
- =
-:---=-----,-
P
(I-
M
a
2
)
F
With regard to the pressure variation the following considerations can be
carried out. From the adiabatic equation follows:
d
-
P
d-
P
d-
'P
=-K-(
I)
P=K-
P
pK
P
K-
P
Thus it holds for the local relative change in pressure
~
=KMa
2dql
P U
1
or with regard to the local relative change
of
the cross-sectional area
of
the
flow:
~2
KMa
elF
(l-M
a
2)
F
Finally it is necessary to consider the variations in temperature. To this
end the state equation for ideal gases is differentiated:
_p
dp +
dP
=Rdf
dF
p2
p F
or transcribed:
dp
dP
df
--+---=---
p P T
Thus follows from the preceding relations
d~
=_(K_I)Ma2dqI
T U
1
The locally occurring relative change in temperature has the opposite sign
of
the local relative change in velocity. The occurring relative changes
in
temperature are weaker than the corresponding relative changes in density.
With regard to the relative area change
of
the flow cross-section it results:
-
~2
dT
(K-I)M
a
dFi
T=
(I-
M
a
2
)
F
The considerations stated for the flow-velocity variation in supersonic
and subsonic flows, can
also be carried out for the variations in pressure,

Stream Tube Theory
235
density and temperature with the aid
of
the above equations. Another important
consideration can be stated through rearrangement
of
the above-derived
relations such that it holds:
d~
=~(1-M(X2)
dV
I
VI
This relation expresses that the condition for achieving the sound velocity
is given by
dF
= 0, i.e.
~
= 1 As for the second derivation holds:
d
2
F
=~M2(M2
-2)
dUt
ut
(X
(X
for M (X = 1 holds a minimum
of
the flow cross-section.
Pressure-driven
Compensating
Flows
through
Converging
Nozzles
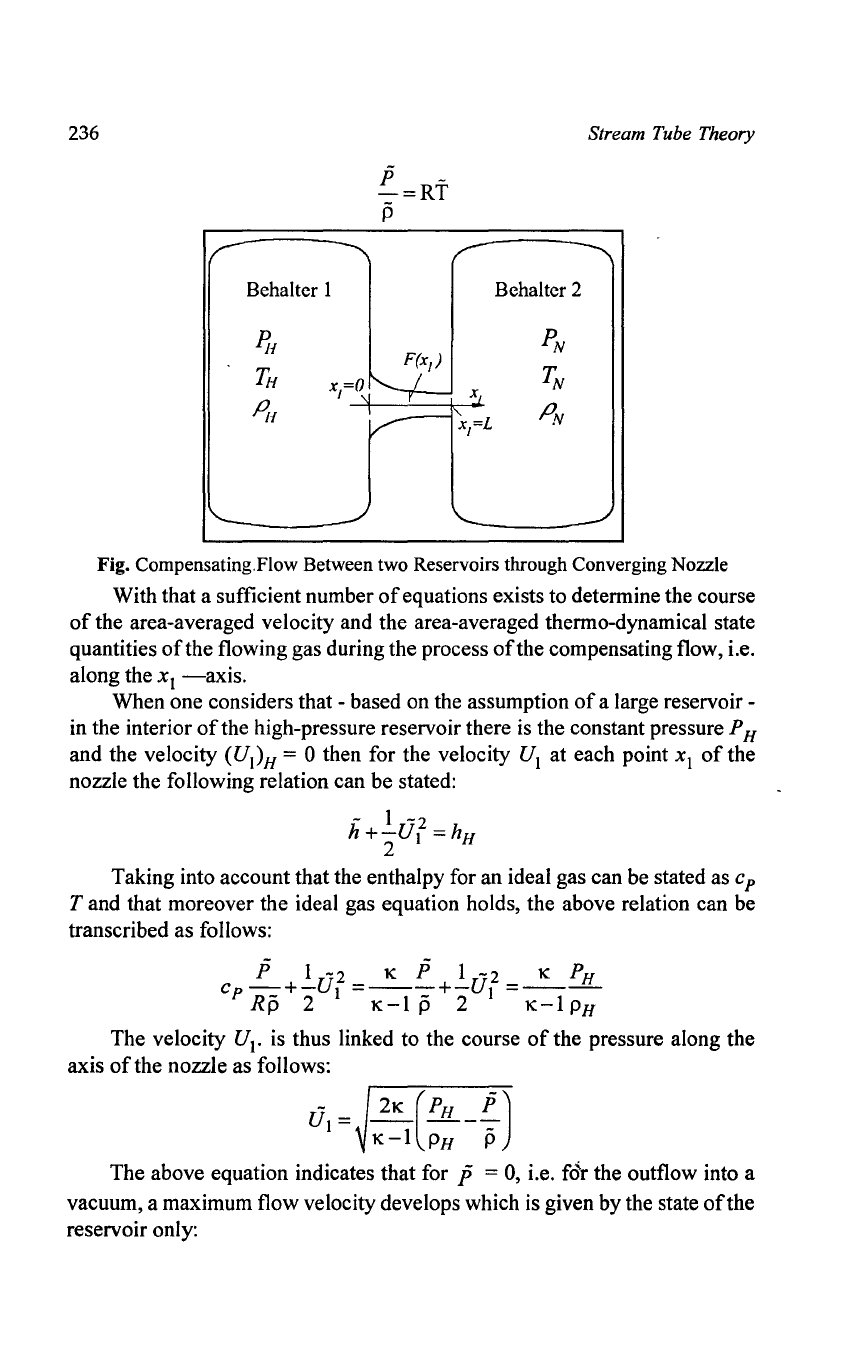
In many technical plants flows
of
gases occur which are to be classified
into the large group
of
compensating flows that can take place between
reservoirs with differing pressure levels. Thus gases e.g. are often stored under
high pressure in large storage reservoirs,
in
order to be led via correspondingly
dimensioned/designed openings with connecting aggregates and discharge
conduits to the intended purpose when need arises.
This discharge can idealized
be
understood as a compensating flow
between two reservoirs
or
two chambers
of
which one represents the storage
reservoir under pressure, while the environment represents the second reservoir.
In the following considerations it is assumed that both reservoirs are very large
so that constant reservoir conditions exist during the entire compensating flow
under investigation. These are assumed to be known and are given by the
pressure
PH'
the temperature T H etc. in the high-pressure reservoir, as well as
through the pressure
P
N
or.
TN
for the low-pressure reservoir. The compensating flow shall
take place via a continually converging nozzle, whose largest cross-section
represents thus the discharge opening
of
the large reservoir, whereas the
smallest nozzle cross-section represents the entrance/inlet opening into the
low-pressure reservoir.
When one wants to investigate the fluid flows taking place in the above
compensating flow more in detail, the final equations for flows through
channels, pipes etc.
pUIF
=const
- 1
-2
P
h +
-V
I = const; - = const
2
pK
236
Behaltcr 1
P -
-=RT
is
Stream Tube Theory
Bchaltcr 2
'----.---~
Fig. Compensating. Flow Between two Reservoirs through Converging Nozzle
With that a sufficient number
of
equations exists to determine the course
of
the area-averaged velocity and the area-averaged thermo-dynamical state
quantities
ofthe
flowing gas during the process
ofthe
compensating flow, i.e.
along the
XI
-axis.
When one considers that - based on the assumption
of
a large reservoir -
in the interior
of
the high-pressure reservoir there
is
the constant pressure
PH
and the velocity (UI)H = 0 then for the velocity U
I
at each point
XI
of
the
nozzle the following relation can be stated:
-
1-2
h+-U
I
=h
H
2
Taking into account that the enthalpy for an ideal gas can be stated as
c
p
T and that moreover the ideal gas equation holds, the above relation can be
transcribed as follows:
P 1
-2
K P 1
-2
K
PH
Cp
-+-U
I
=---+-U
I
=----
RiS
2
K-l
is
2
K-l
PH
The velocity
UI'
is
thus linked to the course
of
the pressure along the
axis
of
the nozzle as follows:
0
1
=
~(PH
_~)
K-l
PH
P
The above equation indicates that for P = 0, i.e. far the outflow into a
vacuum, a maximum flow velocity develops which is given by the state
of
the
reservoir only:

Stream Tube Theory 237
tK
PH
~
V
max
=
----=
2c
p
·T
H
K-l
PH
Standardizing the flow velocity VI' with V
max
'
existing
at
a Point
xI'
one
obtains:
u\
~~l_P'PH
V
max
PH
.p
or
transcribed
by
means
of
the ideal gas equation:
U
I
_
rr
V
max
f-r;;
Linking the adiabatic equation to the state equation the following relations:
f
(p
)K-I
f
(P
)K:I
T H =
PH
and T H =
PH
Thus
the
following equations hold:
~------=
l-(!
rl
V
max
and
VI
=
V
max
l-(~
fJ
When
choosing
the standardized velocity
(V
I I V max)
as
a parameter for
the
representation
of
the
flow in the nozzle, the course
of
pressure, density
and
temperature
can
be
stated as follows:
K
~=[1_(~)2lK-1
PH
V
max
K
.l..-=[1_(~)2lK-1
PH
V
max
:L=[1-(~)2l
TH
V
max
These relations are sated in Figure as functions
of
(VI
IV
max) Also stated
238
Stream Tube Theory
is, along the
(rJ
I I U max)
-axis,
the corresponding Mach number
of
the flow,
which in consideration
of
the
relation
c =
~(
dP
I dp
)ad
= .JKRT
can
be
computed as follows:
rJ?
=
rJ?
KRT
=M2
K-l(
T )
U
2
2c
T
KRT
al
2 T
max
P H H
When one considers the relation derived above for (TIT
H)
equation, one
obtains for the Mach number to be determined:.
Thus a Mach number
of
the flow is to be assigned to each statement
of
an area-averaged velocity standardized with the maximum velocity.
All quantities which are stated in the above equations can also be written
as functions
of
the Mach number 'if;. which in turn is to be considered as
an
area-averaged flow quantity describing the course
of
the flow along the
Xl
-
axis.
For
the derivation
of
the dependency
of
the pressure, the density and
the
temperature from the Mach number
of
the flow, equation is written as follows:
-
1-2
CpT
+-U
I
=cpT
H
2
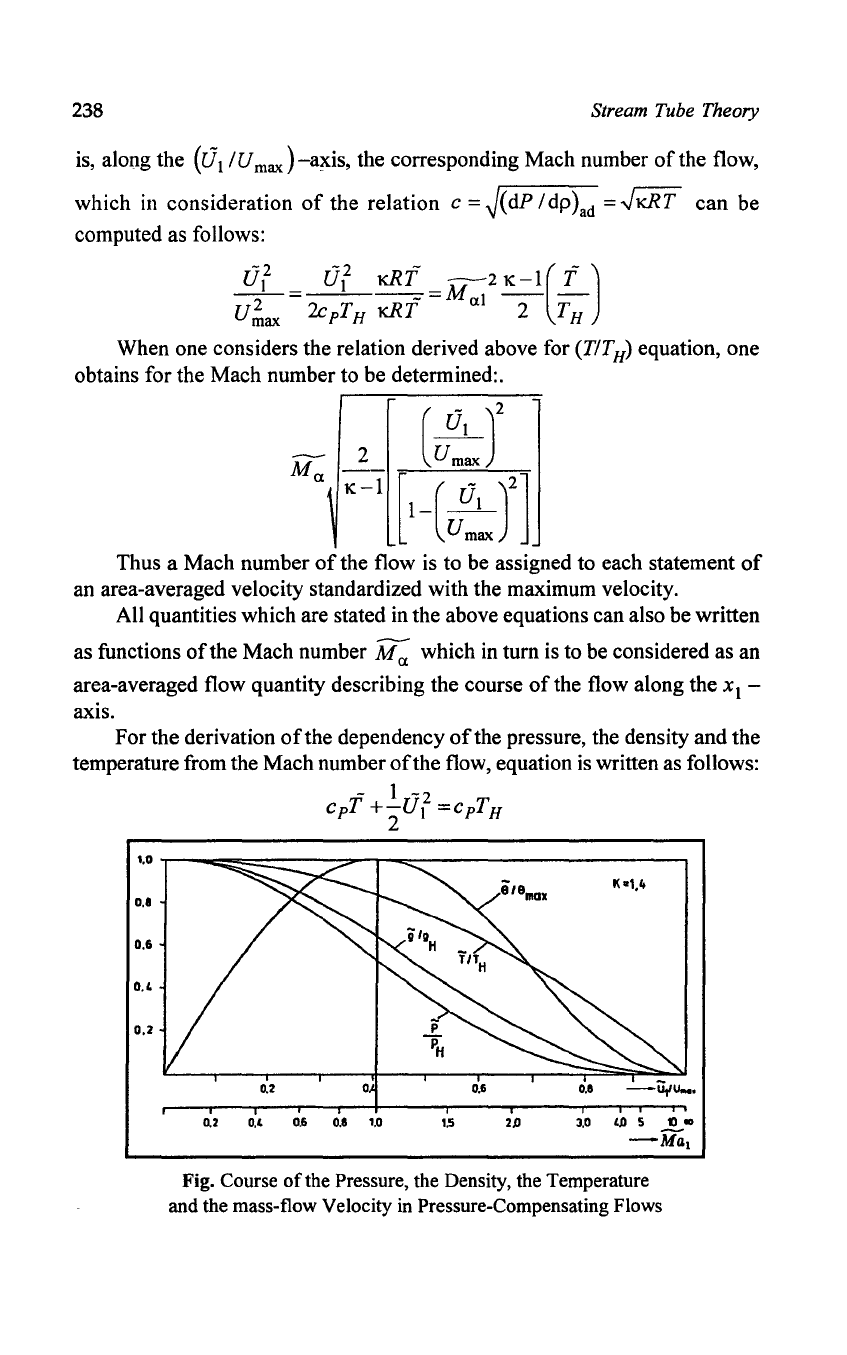
1.0
r--oc::::::~::::=---;:;::=-r-o:::;::------------'
D,I
0.&
0.4
0.2
0.2
0,4 0.6
D..
I,D
1.5
2JJ
Fig. Course
of
the Pressure, the Density, the Temperature
and the mass-flow Velocity
in
Pressure-Compensating
Flows

Stream Tube Theory
By
division with c
pi
one obtains:
-2
Tl!
=1+
U
I
_
KR
=1+
K-I
M
2
H
2c
p
T
KR
2
al
or
for the reciprocal:
i 2
-=-----:==
T H 2 + (K
-I)
M
af
239
This equation makes it clear that a relation is given between the area-
averaged temperature along the
x I - axis and the Mach number existing at the
same point
of
the flow.
With this for each
xI
- point the temperature can be computed, when
the
reservoir state is given and the Mach number
of
the flow known.
Taking into account the adiabatic equation, for the relation
of
pressure
and reservoir pressure results:
K
-
(-)~
[
]K-I
P T
K-I
2
PH
=
TH
=
2+(K-I)
Ma
r
and
"
p ( i
)K~I
[ 2
],,-1
PH
=
TH
=
2+(K-I)
Ma
r
The mass-flow density e =
Til
IF
=
pOI'
...
, i.e. the statement
of
the mass
flowing per area and time unit through a flow cross-section. The course
of
this quantity can be written as follows, using the relations for
VI
and
p:
"
- - U
I
-2
[
(
-
)21"-1
P.ol
=PH
1-
--
,U
I
U
max
J
or
for the standardized mass-flow density:
"
PIOI
_ 0
1
[I
( 0
1
)2]"-1
pHU
max
-
U
max
-
U
max
The relation indicated above for the mass-flow density makes it clear,
that for
U
I
= 0, e = 0 is achieved. The mass-flow density, however, assumes
the value zero also for
U
I
= U
max
as with setting the maximally possible
velocity the density
of
the fluid also contained in the mass-flow density has

240
Stream Tube Theory
dropped to p =
O.
Between these two minimal values the mass-flow density
has to traverse a maximum which can be computed by differentiation
of
the
above functions and by setting the derivation to zero. The value obtained by
solving the resulting equation has to be inserted for
CUI
IUmax)
in the above
equation for the mass-flow density
in
order to achieve the maximal value. It
is
computed:
~(
2
)K~I
9
max
=PH
·U
max
·V~
K+l
where for the velocity value it
is
obtained:
U
I
J§-l
--=
--
for9=9
max
U
max
K+l
With this the mass-flow density standardized with the maximal value can
be written as follows:
I
9
~
U
I
[K+l[
UI21lK-I
9
max
=
,,~
. U max
-2-
1-
U max
The course
of
this quantity with UIIU max
is
also represented. The
significance
of
the maximum
of
the mass-flow density for the course
of
compensating flows is dealt with more in detail further down. Its appearance
prevents the steady increase
of
the mass flow with the increase
of
the pressure
difference between pressure reservoirs when the compensating flow takes place
via steadily converging nozzles.
A representation
of
the compensating flows through converging nozzles
often regarded to be more simple is achieved by relating the quantities
designating the flow to the corresponding quantities
of
the "critical state",
which is designated by
Mu
= 1 To this state corresponds not only a certain
Mach number, i.e.
MCJ:;.
= 1, but also certain values
of
the thermo-dynamic
state quantities: These can be determined from the equations by setting
MCJ:;.
= 1 From this result the following values for thermo-dynamic state
quantities
of
the fluid in critical state, i.e. for
MCJ:;.
= 1 :
Stream Tube Theory
241
t* 2
-=--
TH
K+l
With these equations the pressure, density and temperature
of
a flowing
medium can be determined in that cross-section
of
a converging nozzle
in
which the sound velocity occurs.
According to the considerations carried out a minimum
of
the cross-section
has to exist at this point. As at this point the Mach number assumes the value
M
<XI
= 1 the equation can be written as follows:
-*2
( - )
U
I
_K-l
T
_K-l
U
2
max
-
-2-
T H - K + 1
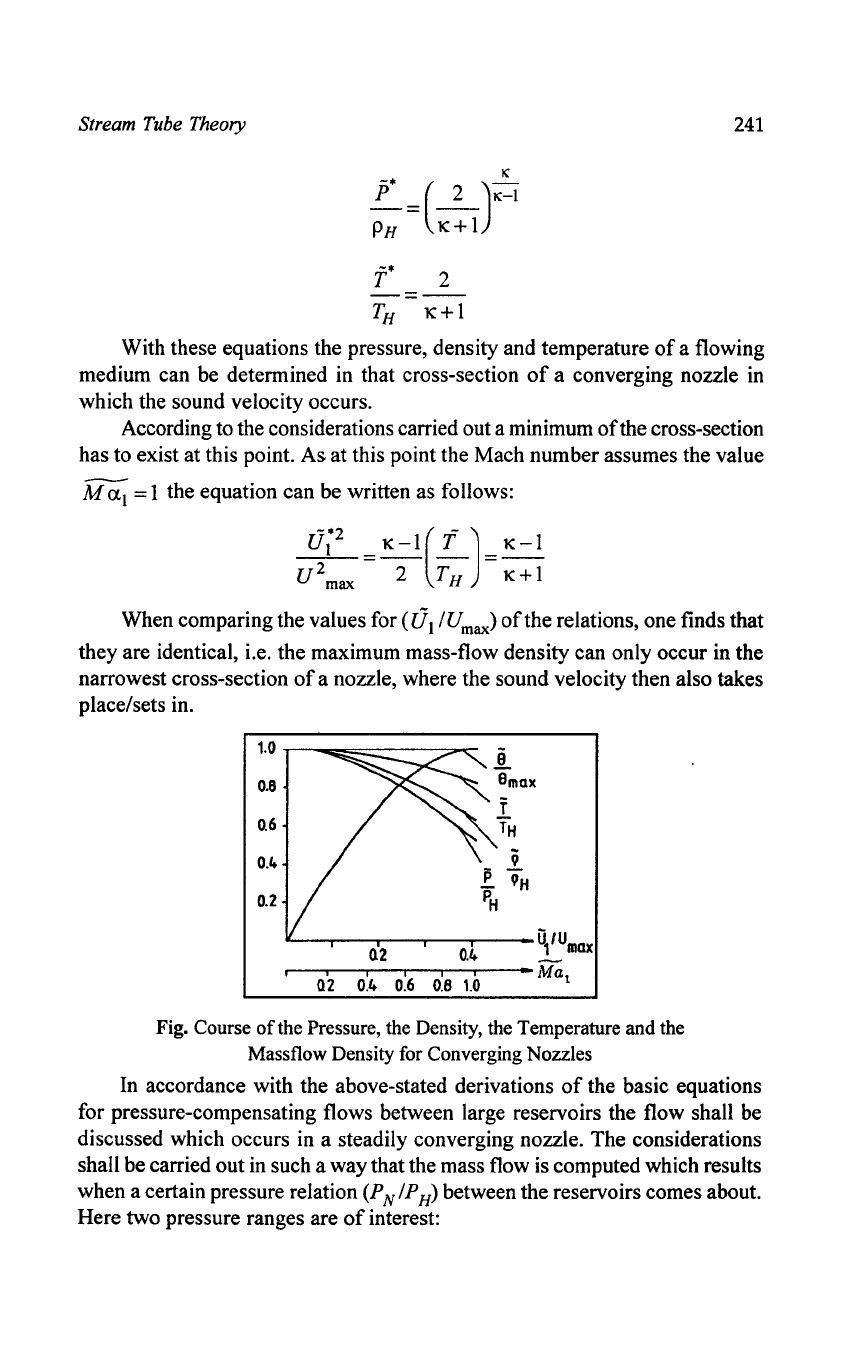
When comparing the values for (
rJ
I / U max)
of
the relations, one finds that
they are identical, i.e. the maximum mass-flow density can only occur in the
narrowest cross-section
of
a nozzle, where the sound velocity then also takes
place/sets in.
1.0
0.8
8
max
T
0.6
TH
0.4
0.2
Fig. Course
of
the Pressure, the Density, the Temperature and the
Massflow Density for Converging Nozzles
In accordance with the above-stated derivations
of
the basic equations
for pressure-compensating flows between large reservoirs the flow shall be
discussed which occurs
in
a steadily converging nozzle. The considerations
shall be carried out
in
such a way that the mass flow
is
computed which results
when a certain pressure relation
(P N / P H) between the reservoirs comes about.
Here two pressure ranges are
of
interest:
