Brewster H.D. Fluid Mechanics
Подождите немного. Документ загружается.

242
Stream Tube Theory
The relation
of
the reservoir pressures
is
larger than
the critical pressure relation
P
N
P * The relation
of
the reservoir pressures
is
smaller than
-<-
PH
PH
the critical pressure relation
When the pressure relation is larger than the critical value, a steady
decrease
of
the relation
of
the reservoir pressures leads to a steady increase
of
the mass-flow density.
L-
____________________
_
U,
u
....
"-1
----,~---.--~------,-
111
a.!
0.0
1.0
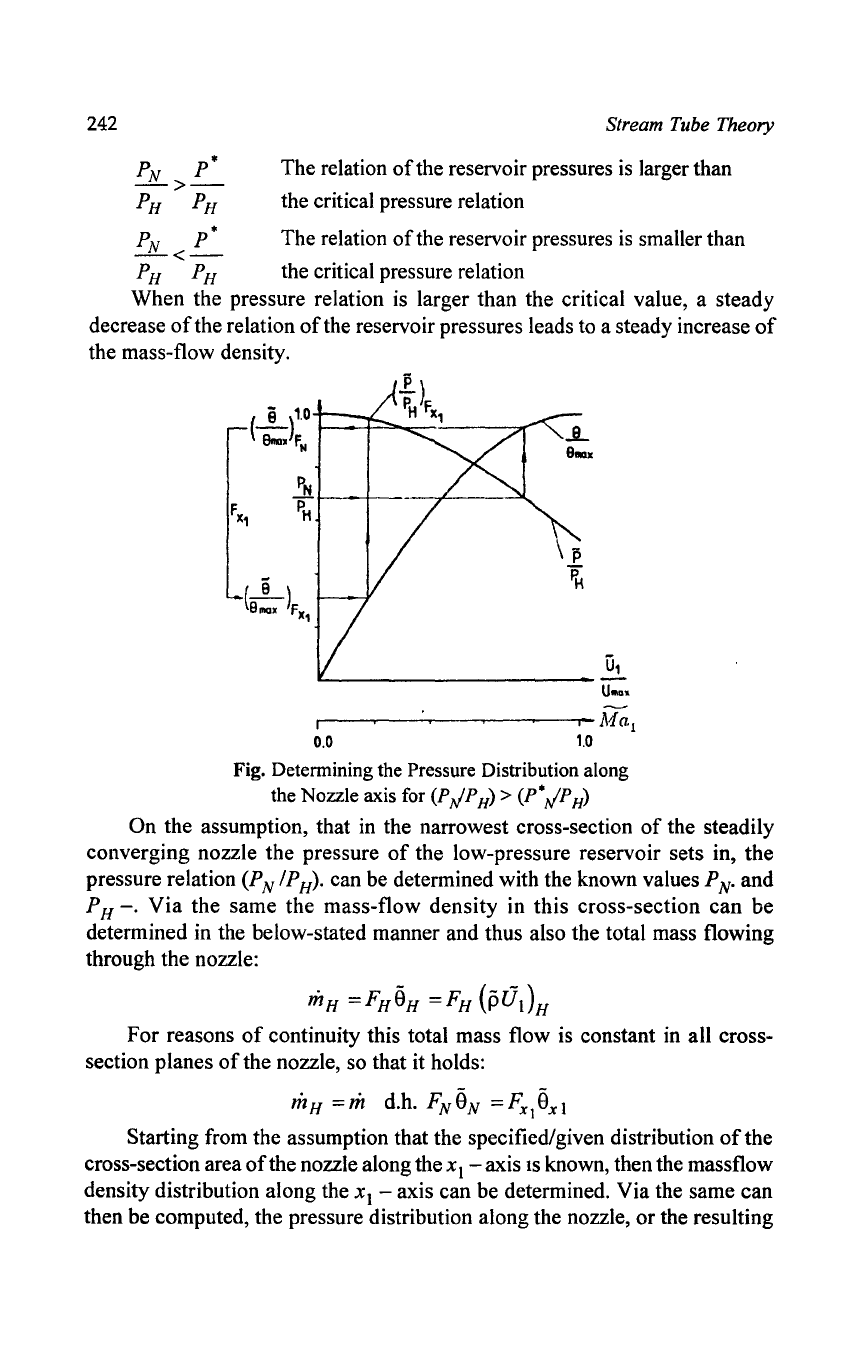
Fig. Determining the Pressure Distribution along
the Nozzle axis for
(P,IP
H
)
> (P*tlPH)
On the assumption, that in the narrowest cross-section
of
the steadily
converging nozzle the pressure
of
the low-pressure reservoir sets in, the
pressure relation
(P
N / PH)' can be determined with the known values P
N'
and
PH
-.
Via
the same the mass-flow density in this cross-section
can
be
determined in the below-stated manner and thus also the total mass flowing
through the nozzle:
mH
=FHe
H
=F
H
(pUI)H
For reasons
of
continuity this total mass flow is constant in all cross-
section planes
of
the nozzle, so that it holds:
mH
=m
d.h.
FNe
N
=Fxte
xi
Starting from the assumption that the specified/given distribution
of
the
cross-section area
of
the nozzle along the x I - axis IS known, then the massflow
density distribution along the
xl
- axis can be determined. Via the same can
then be computed, the pressure distribution along the nozzle, or the resulting
Stream Tube Theory
243
distributions
of
the density and the temperature, but also
of
the Mach number
and the flow velocity.
9
1.0-.---_
t
(g
..
••
)FN
!tt.
Fx
P.
~----~-~
1 H
~)
8"0>
Fx,
U,
L-
__
~________
UMI
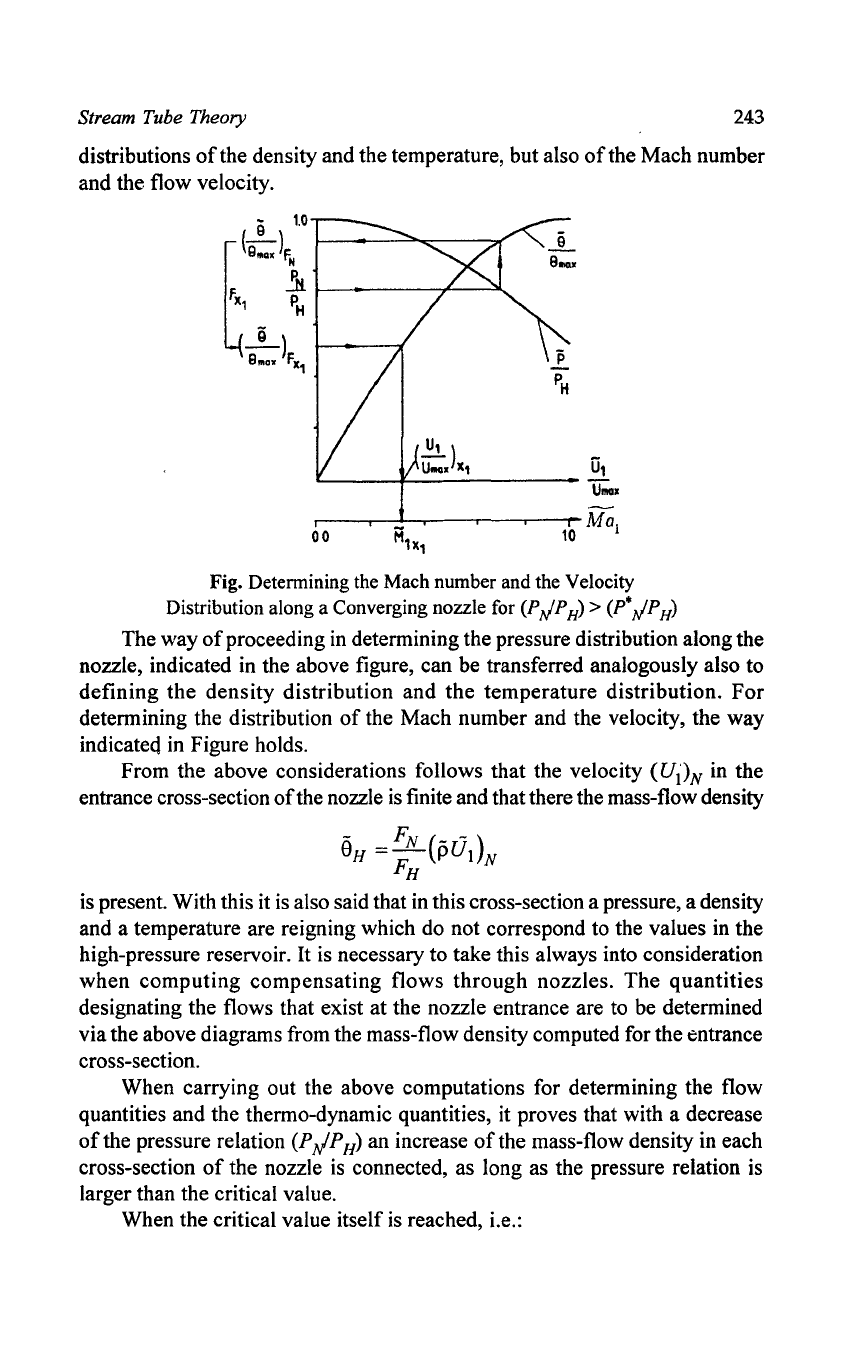
Fig. Determining the Mach number and the Velocity
Distribution along a Converging nozzle for
(P"; P
H)
> (p.,.; P
H)
The way
of
proceeding in determining the pressure distribution along the
nozzle, indicated in the above figure, can be transferred analogously also to
defining the density distribution and the temperature distribution.
For
determining the distribution
of
the Mach number and the velocity, the way
indicated in Figure holds.
From the above considerations follows that the velocity
(UDN in the
entrance cross-section ofthe nozzle
is
finite and that there the mass-flow density
9
H
=
FN
(pU\)N
FH
is present. With this it
is
also said that in this cross-section a pressure, a density
and a temperature are reigning which do not correspond to the values
in
the
high-pressure reservoir.
It
is
necessary to take this always into consideration
when computing compensating flows through nozzles. The quantities
designating the flows that exist at the nozzle entrance are to be determined
via the above diagrams from the mass-flow density computed for the entrance
cross-section.
When carrying out the above computations for determining the flow
quantities and the thermo-dynamic quantities, it proves that with a decrease
of
the pressure relation
(PJP
H
)
an increase
of
the mass-flow density in each
cross-section
of
the nozzle
is
connected, as long as the pressure relation is
larger than the critical value.
When the critical value itself
is
reached, i.e.:

244 Stream Tube Theory
K
~:
=(K!JK-l
=
;:
This value cannot be exceeded in the case
of
a further decrease
of
the
pressure relation
(P
J PH) i.e. for all pressure relations smaller than the critical value:
K
P
N
< P * =
(_2_)K-l
PH PH
K+l
in the steadily converging nozzle a flow comes about which is identical for all
pressure relations.
At
the exit cross-section
of
the nozzle, i.e. in the entrance
cross-section to the low-pressure reservoir, the pressure
P N does not come
about any more. In this cross-section the maximum mass-flow density rather
is reached:
emax
=
PH
~2cpT
H
The
total mass flow thus is computed:
m
=mmax
=FNe
max
Starting again from the assumption that the nozzle form is known, then
the mass-flow distribution existing along the axis can be computed via the
continuity equation. When this distribution is known, the corresponding
distributions
of
the pressure, the density, the temperature, the Mach number
and the flow velocity can be determined.
Of
importance is that for all pressure
relations
(P
N / PH)' that are equal
or
smaller than the critical relation, one and
the same flow comes about in the nozzle. In the exit cross-section
of
the nozzle
for an area-averaged pressure exists which is larger than the pressure
P
N'
existing in the low-pressure reservoir.
K
~v
< p * =
(_2_)K-l
PH PH
K+l
The pressure compensation takes place via fluid flows that form in the
open-jet flow, stretching from the nozzle tip to the interior to the low-pressure
reservoir.
Finally attention is drawn to important facts
of
the case which shall serve
the comprehension
of
the occurring compensating flow. The above represen
tations started from the state often existing in practice that compensating flows
are controlled via pressure differences between reservoirs. This means that it
..
Stream Tube Theory
245
was assumed that PH'
PH
or T H are known and constant and that they have an
influence on how the flow forms.
PH
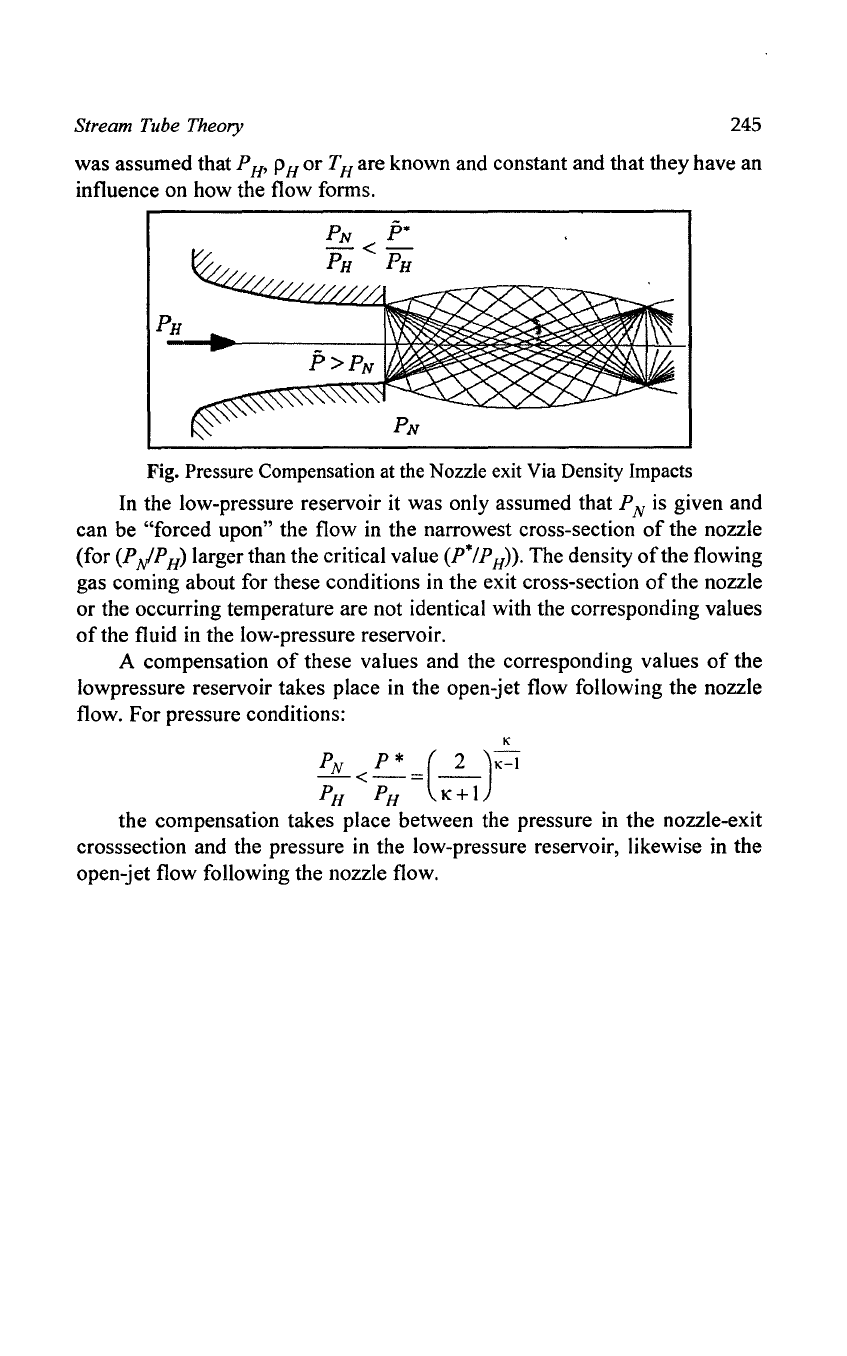
Fig. Pressure Compensation at the Nozzle exit Via Density Impacts
In
the low-pressure reservoir it was only assumed that P N is given and
can be
"forced upon" the flow in the narrowest cross-section
of
the nozzle
(for
(PJP
H
)
larger than the critical value (P*IP
H
».
The density
of
the flowing
gas coming about for these conditions in the exit cross-section
of
the nozzle
or the occurring temperature are not identical with the corresponding values
of
the fluid in the low-pressure reservoir.
A compensation
of
these values and the corresponding values
of
the
lowpressure reservoir takes place
in
the open-jet flow following the nozzle
flow. For pressure conditions:
I(
PN < P * =
(_2_)1(-1
PH PH
K+l
the compensation takes place between the pressure in the nozzle-exit
crosssection and the pressure
in
the low-pressure reservoir, likewise in the
open-jet flow following the nozzle flow.
Chapter 9
Potential
Flows
lJp
(p+
lJx2
AX2
)AF
2
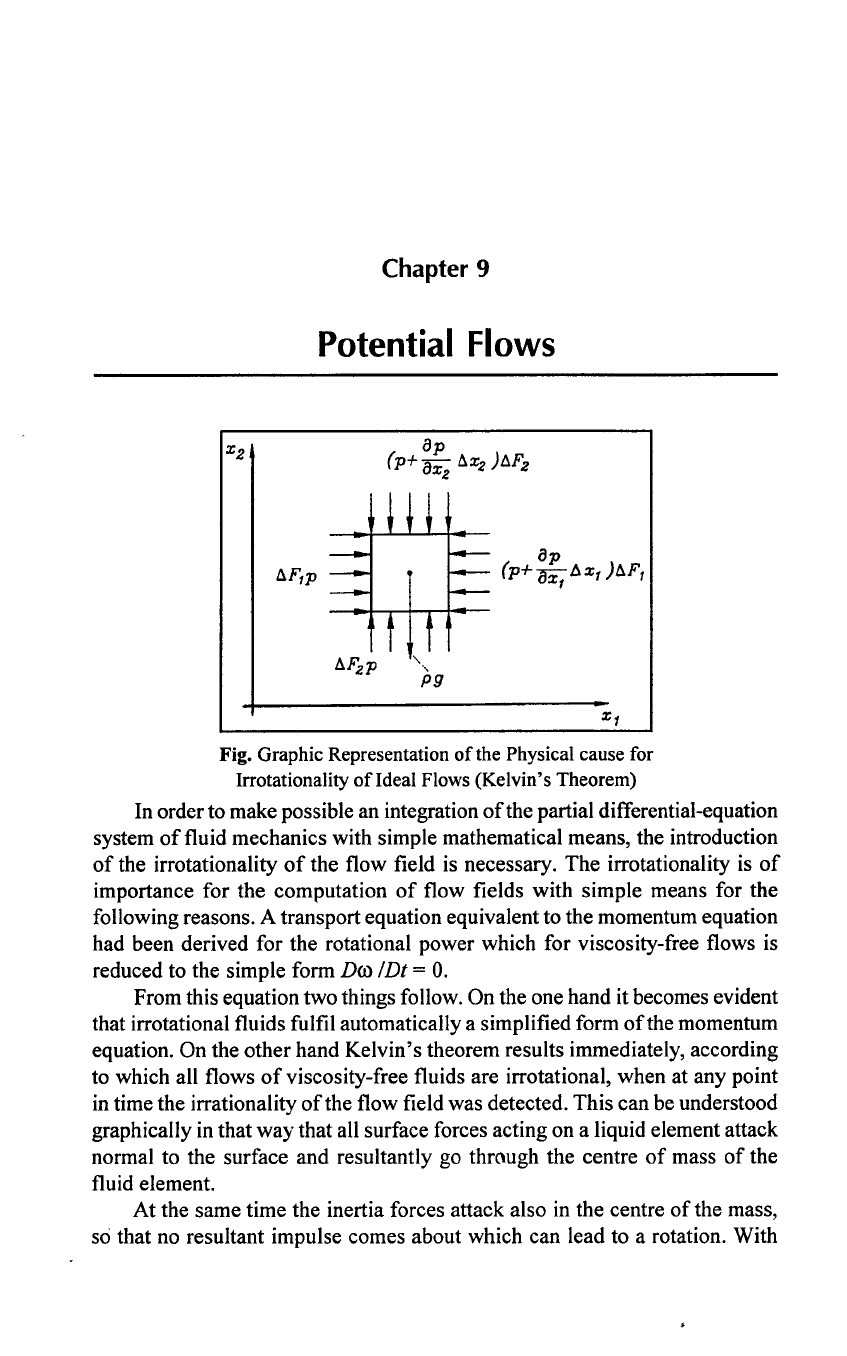
Fig. Graphic Representation
of
the Physical cause for
Irrotationality
ofIdeal
Flows (Kelvin's Theorem)
In order to make possible an integration
of
the partial differential-equation
system
of
fluid mechanics with simple mathematical means, the introduction
of
the irrotationality
of
the flow field is necessary. The irrotationality is
of
importance for the computation
of
flow fields with simple means for the
following reasons. A transport equation equivalent to the momentum equation
had been derived for the rotational power which for viscosity-free flows is
reduced to the simple form
DID
IDt
=
O.
From this equation two things follow. On the one hand it becomes evident
that irrotational fluids fulfil automatically a simplified form
of
the momentum
equation.
On the other hand Kelvin's theorem results immediately, according
to which all flows
of
viscosity-free fluids are irrotational, when at any point
in time the irrationality
of
the flow field was detected. This can be understood
graphically in that way that all surface forces acting on a liquid element attack
normal to the surface and resultantly go
through the centre
of
mass
of
the
fluid element.
At the same time the inertia forces attack also in the centre
of
the mass,
so that
no
resultant impulse comes about which can lead to a rotation. With

Potential Flows
247
this the conclusion is possible that rotating parts cannot receive an additional
rotation by the pressure and inertia forces acting on ideal fluids. In addition to
the above demand for irrotationality a further restriction shall now be made as
regards the properties
ofthe
flows, namely the exclusive consideration
of
two-
dimensional flows. This restriction is not a condition
of
the demand for
irrotationality; one can on the contrary very well imagine three-dimensional
flows
of
viscosity-free fluids that are irrotational. For twodimensional
irrotational flows there exists, however, a very elegant solution method which
is based
on
the employment
of
complex analytical functions and which is used
exclusively in the following.
When occupying oneself with two - dimensional flow fields, the only
remaining component
of
the rotational vector reads:
0)3
=!(au
2
_
au!)
2
ax!
aX2
When one assumes two-dimensional flow fields to
be
irrotational, it holds
co= 0 or:
au!
aU
2
--=~-
ax
2
ax!
This condition has to be fulfilled when two-dimensional flow problems
are to be solved.
Disregarding singularities, for irrotational flow fields the above relation
has to be fulfilled in all points
of
the flow field. This
is
tantamount to the
statement that for two-dimensional irrotational flows a velocity potential
driving the flow
<I>(x
l'
x
2
)
exists, to such an extent that the following relations
hold:
8<1>
8<1>
U
t
=-
and U
2
=-.
ax
t
aX2
Equation leads to the following relations:
au
1 a
2
<1>
au
2 a
2<1>
--=
=--=
,
ax
2
ax
lax
2
aXt
ax
taX
2
which for irrotational flow fields, i.e. for
co
3
= 0, confirm the reasonable
introduction
of
a potential driving the velocity field. When one inserts the
relations into the two-dimensional continuity equation for p
= const then one
obtains the Laplace equation for the velocity potential:
a
2
<1>
a
2
<1>
--+--=0
aXfaxi .
For determining two-dimensional potential fields it is sufficient to solve
equations, i.e. for determining the velocity field it is not necessary to solve

248
Potential Flows
the Navier-Stokes equation formulated in velocity terms. These equations have
to be employed, however, for determining the pressure field.
The solution
of
the partial differential equations for the velocity potential
requires at the boundary flow the boundary condition
acD
= 0
an
'
where n is the normal unit vector at each point
of
the boundary flow.
When the velocity potential or potential field
cD
has been obtained as a
solution
of
equation, the velocity components U
I
and U
2
can be determined
for each point
of
the flow field by partial differentiations, according to the
relations. After that determining the pressure via Euler's equations, i.e. via
the momentum equations for viscosity-free fluids takes place. Determining
the pressure can, however, also be done via the integrated form
of
Euler's
equations, which leads to the
"non-stationary Bernoulli equation".
The above representations make it clear that the introduction
of
the
irrotationality
of
the flow field has led to considerable simplifications
of
the
solution ansatz for the basic equations for flow problems. The equations that
have to be solved for the flow field are linear and they can be solved decoupled
from the pressure field.
The linearity
of
the equations to be solved is an essential property as it
permits the superposition
of
individual solutions
of
the equations in order to
obtain also solutions
of
complex flow fields. This solution principle will be
used extensively
in
the following sections.
In the derivations
of
the above equations for two-dimensional potential
flows the potential function was introduced in such a way that the irrotationality
of
the flow field was fulfilled identically. The introduction
of
the potential
function
cDi
into the continuity equation then led to the two-dimensional
Laplace equation; only such functions
cD,
which fulfil this equation can be
regarded as solutions
of
the basic equations
of
irrotational flows.
Via a procedure similar to the above procedure for the introduction
of
the potential function
<ll
"it
is
possible to introduce a second important function
for two-dimsnional flows
of
incompressible fluids, the so-called stream
function
'P. The latter is defined in such a way that through the stream function
the two-dimensional continuity equation is automatically fulfilled, i.e.:
a'P
a'P
U
I
=-
and U
2
=--.
aX2
aXI
This relation inserted into the continuity equation shows directly that the
stream function
'P. introduced according to fulfils this equation; per definition
this
is
the case for rotational and irrotational flow fields.
When one wants to define analytically or numerically the stream function

Potential Flows
249
of
an irrotational flow, a potential flow,
qI
has to be a solution
of
the Laplace
equation
a
2
qI a
2
qI
--+--=0
axfaxi
as can be derived by inserting the equations into the condition for the
irrotationality.
au
2
_au
l
=0
aXI
ax
2
The stream function for two-dimensional potential flows fulfils the
twodimensional Laplace equation, similar to the potential function
<1>.
The stream function has a number
of
properties that prove useful for the
treatment
of
two-dimensional flow problems. Lines
of
constant stream function
values for example are path lines
of
the flow field when stationary conditions
exist. This can be derived by stating the total differential
of
qI
:
aqI aqI
dqI=-dx
l
+-dx
2
·
ax
l
ax
2
For
qI
= const
is
d'I' = 0 and thus results:
%2
mp
(
dx
2
)
aXI
U
2
dx
I
'I'
=const = - aqI =
"'if;
ax
2
Fig.
Schematic
Representation
of
the
Flow
Between
Flow
Lines
This is the relation for the gradient
of
the tangent
of
the flow line, but
also for the gradient
of
the path line
of
a fluid element.
. Accordingly the total family
of
flow lines
of
a velocity field
is
described
by all sorts
of
qI
- values.
A further essential property
of
the stream function becomes clear by the
fact that the difference
of
the stream-function values
of
two flow lines indicates
the volume stream that flows between the flow lines. When computing the

250
Potential Flows
volume stream that passes the control area in flow direction for an area
AB
mit with the depth
1,
one ohtains:
B B B
Q=
JU
I
dx
2
-
JU
2
dx
I
=
J(U
I
dx
2
-U
2
dx
I
).
A A A
It
holds, however:
d'I'
= U
I
dx
2
-
U
2
dx
I
,
so that can be written:
B B
Q=
J(U
I
dx
2
-U
2
dx
I
)=
Jd'I'='I'B
-'I'A'
A A
It
is
remarked that from the statement that
'I'
= const are flow lines
of
the flow field follows
of
course immediately the condition that fixed walls
have
to
run tangentially
to
lines
'I'
=
const
From
the
orthogonality
of
equipotential and flow lines which is shown in the following section results at
once that equipotential lines always have to stand vertically on fixed walls.
When one considers the streamlines that can be stated for two-dimensional
potential flows in connection with the potential lines
of
the same flow field,
i.e. lines with
<I>
= const, one finds that these lie orthogonally to one another.
This can be shown by stating the total differential
d<l>,
8<1> 8<1>
d¢=-dx
I
+-
dx
2,
ax
i
8x2
or writing same under consideration
of
equation as follows:
d<l>
= U
I
.
dx
I
+ U
2
dx
2
.
The lines
<I>
=.
are thus given
by
(
8X2)
=_~
ax
1 !l>=const U 2
A comparison
of
the relations yields:
(:~t
=
1
As the gradient
of
the equipotential lines
is
equal to the negative reciprocal
ofthe
gradient
of
the flow lines, these lines form an orthogonal net. The velocity
along a stream can be computed as:
Us
=(:)~
This relation is often used in investigations
of
flow fields for which values
of
flow lines and equipotential lines have been computed
or
obtained from
measurements.
From the above derivations it is comprehensible that a stream function
'I'

Potential Flows
251
can be computed when the potential function
<l>
is known and that also inversely
the potential function
<l>
can be determined when the stream function
'II
is
available. The procedure for determining one function from the other
is
to be
regarded in accordance with the below-stated single steps for determining the
stream function:
• The known potential function
<l>(x,
y)
is examined with regard to
whether it represents a solution
of
equation.
• By partial deriving to
xI
and x
2
the velocity components U
I
and U
2
are determined, in accordance with relations.
• From this can be determined the gradient
of
the equipotential lines,
(:~)~
=-
~~
• Equation follows for the gradient
of
the flow lines:
(
dx
2
)
U2
dx
l
'I'
=
u-;
• By integration
of
this relation the course
of
the flow line IS
conserved. These are lines
of
constant 'II - values.
POTENTIAL
AND
COMPLEX
FUNCTIONS
The representations have shown that the velocities U
I
and U
2
can
be
stated
as partial derivations
of
the stream function and the potential function for
irrotational two-dimensional flows
of
incompressible and viscosity-free fluids:
and
8<I>
a'¥
U
I
=-=-
ax
l
ax
2
8<I>
a'¥
U
2
=-=--·
aX2
aXI
On the basis
of
their definition the stream and potential function satisfy
the Cauchy-Rieman differential equations:
8<I>
a'¥
ax
l
=
ax
2
'
8<I>
a'¥
--=--
aX2
ax
l
This gives expression to that a complex analytical function F (z) can be
stated
in
which
<l>(x,
y)
represents the real part and 'II (x,
y)
the imaginary part
of
the function F(z) is designated as the complex potential
of
the velocity
field F
(z) =
<l>(x,
y)
+
i'¥
(x,
y),
where x =
xI
and y = x
2
can be seen and z = x + iy indicates a point in the
