Brewster H.D. Fluid Mechanics
Подождите немного. Документ загружается.


262
Potential Flows
DIPOLE CURRENT
FLOW
In this section a potential flow shall be discussed which is defined as
dipole current flow and results as a borderline case
of
the superposition
of
a
source flow with a sink flow. Considered is a source with the strength
Q
which
is
located on the
x-axis
in
the distance (-a). from the origin
of
a
coordinate system and a sink
of
the same strength which has been arranged on
the x-axis in the distance
(+a).
(al
(bl
Fig. Flow Lines ofCa) Source and Sink Flows as well as (b) A Dipole Current Flow
When the distance a is reduced, source and sink move closer together
until for the borderline case
a
~
0 they both coincide in the coordinate origin
and thus result into the dipole current flow.
It is the task
of
the below-stated derivations to find the complex potential
of
the dipole current flow and to derive and discuss based on it the flow field
of
the dipole current flow.
The complex potential
of
the combined source and sink flow can
be
stated
as the sum
of
the complex potential
of
both flows:
F(z)=
Q In(z
+oJ-.fLln(z
-a)
2n 2n
or transcribed:
F(z)=
Q
[In(~)]=.fLln[l+a/z
J.
2n z
-a
2n
l-a/z
When carrying out a series expansion for the tenn
(1-
~
/ z ) one obtains:
F(z)~
;~
10[(1+:
)(1+:
+
:~
+
::
+
..
)]

Potential Flows
or after perfonned multiplication:
F(z
) =
~ln(l
+ 2
a)
21t
z
When one carries out another series expansion:
(
a)
a a
2
Sa
3
In
1+2--
=2--2-+-+···
z z z 2 3z 3
one obtains for small values (a/z)
Q a
F(z)=-2-.
21t
z
With the strength/force
of
the dipole current flow:
D=Qa
1t
results as complex potential:
F(z)=D
= D
z
(x
+ iy )
263
For the potential and stream function the following tenns can be derived:
(
Dx (
-Dy
<I>
r,
<p)
= 2 2 and
'¥
r,
<p)
= 2 2
x
+y
x
+y
(
D
-D
<I>
r
,<p)
=-
cos<p
and
'¥(r
,<p)
=
-sin<p
r r
The flow lines and equipotential lines are indicated. For the complex
velocity can be derived:
or transcribed:
w
(Z)=
dF(x)
_~=_~e(-i2<9)
dz
z 2 r2
w
(z
)=-~(COS<P-i
sin <p)e(-i
2<9)
r2
From this result the velocity components:
U
r
= -
~
cos<p
and U
<9
= -
~
sin<p.
r r
The signs
of
these velocity components confinn the direction
of
the flow
indicated.
POTENTIAL FLOWS
AROUND
A CYLINDER
The significance
of
the dipole current flow lies in the fact that its complex
potential can be superimposed with the complex potential
of
the unifonn flow
parallel to the x-axis and that thus a complex potential arises which describes
the flow around a cylinder. The simple superposition
of
the F (z)-functions
264
Potential Flows
of
flows
is
admissible as the partial differential equations derived from the
basic equations
of
flow mechanics are linear for the potential and stream
function. By addition
of
the complex potentials for the even flow parallel to
the x-axis and for the dipole
cl!rrent flow one obtains the following relation:
F (z ) = U
OZ
+ D = U
ore
(i
<p)
+ D e (-;
<p)
,
Z r
which is equivalent to
F (z ) = U
or
( cos
<p
+ i sin
<p)
+ D (cos
<p
- i sin
<p).
r
For the potential and stream function thus the following terms can be
found:
<I>(r.<p)=(
Uor
+
~
)cos<p and
'P(r,<p)=(
Uor
-
~
)sin<p.
When one inserts now the radius r = R
of
a cylinder, the stream function
along a cylinder wall results as:
'P(r
,<p)
=
(U
oR
-
~
)sin<p.
~~
______________
X1
x
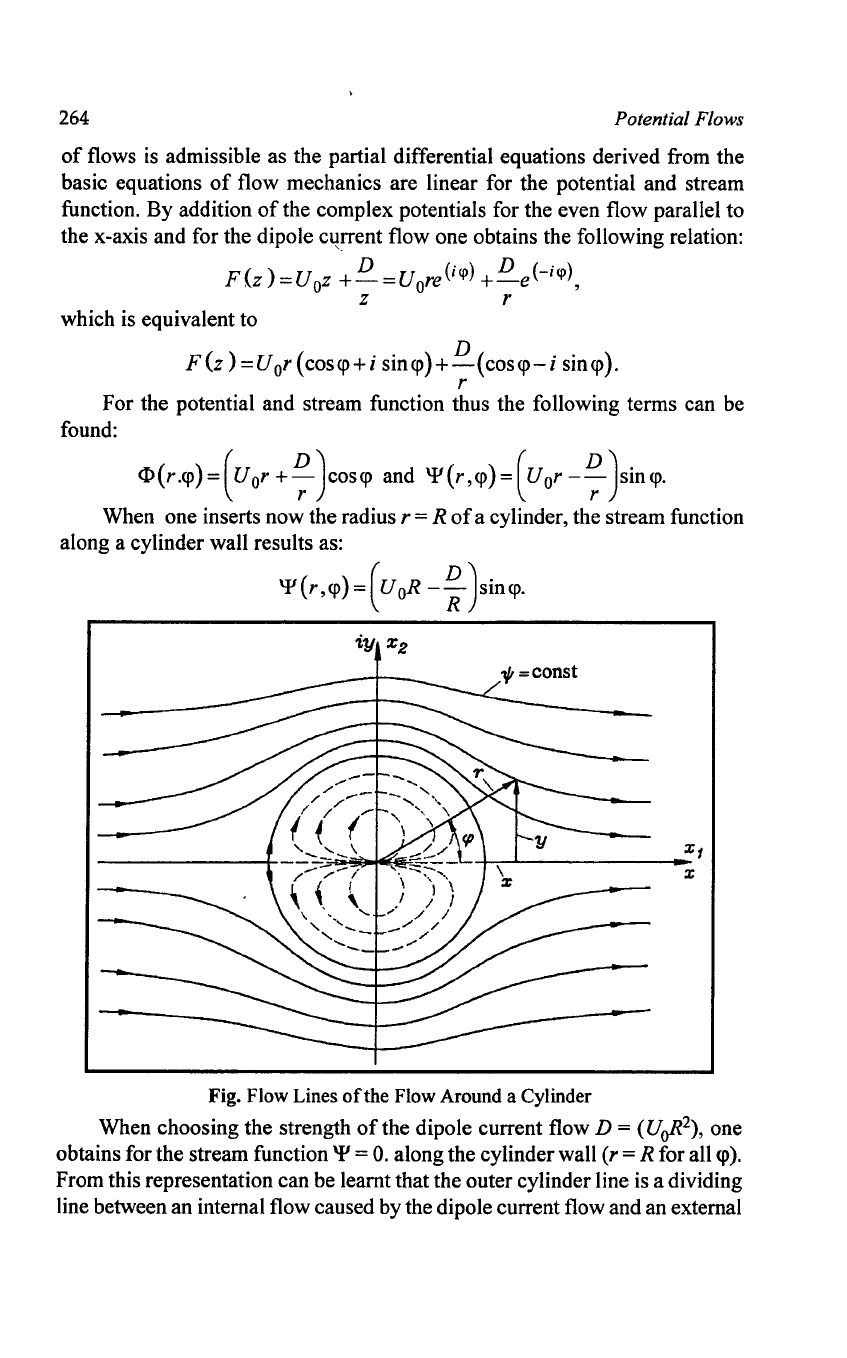
Fig. Flow Lines
of
the Flow Around a Cylinder
When choosing the strength
of
the dipole current flow D = (UoR
2
),
one
obtains for the stream function
'P
=
O.
along the cylinder wall
(r
= R for all
<p).
From this representation can be learnt that the outer cylinder line is a dividing
line between an internal flow caused by the dipole current flow and an external

Potential Flows
265
flow coming from the flow parallel to the x-axis. We thus have a flow whose
external flow can be interpreted as the flow resulting from a two-dimensional
flow
of
an incompressible viscose-free fluid around a cylinder.
When one takes into consideration the relation
D =
UoR
2
,
derived for the
strength
of
the dipole current flow, for the complex potential
of
the flow around
a cylinder
r
~
R can be stated:
F
(z
) = u 0
(z
+ :
2
).
In addition, for the potential and stream function holds:
<I>{r
,cp)
=U 0 (r +
~2
)coscp and 'I'{r
,cp)
=U 0 (r _
~2
)sincp.
For the complex velocity can be derived:
w
(z)=
dF(z)
=UO(I-
R
2
)=U
O
[I_
R2
e<-i2<P)].
dz z 2
r2
Further conversions yield:
w
(z
)~uo[e(iO)-
~:
e<-iO)]e
HO
),
=UO[{COSCP+i
sincp)-
~:
(coscp-i
sincp)].e<-i<P),
and lead to the following velocity components:
U
r
=UO(I-
~:}oscp
and
U<p
=-UO(I+
~:)sincp.
For the outer cylinder area
(r
= R)
result9:U
t
=
0;
along the circumferential
surface there
is
only a flow in circumferential direction. For the latter results
a velocity component:
U
<P
= -2U 0 sin
cp
for r = R
For
<p
= 1t thus a velocity component exists which
is
equal to twice the
2
value
of
the inflow velocity.
The indicated potential flow
around a cylinder results in a solution having
flow-o conditions which are equal to the inflow conditions, so that no force
resulting from the flow acts on the cylinder. This can also be derived from the
solution for the velocity
fiel<;l
itself. As concerns the quantity
of
the U
j-
component, there exists a symmetry to the x-axis, so that the pressure
distribution
is
also symmetrical and therefore no resulting buoyancy force
comes about. Because
of
a likewise existing symmetry
of
the pressure

266
Potential Flows
distribution
is
also symmetrical
and
therefore
no
resulting buoyancy force comes
about. Because
of
a likewise existing symmetry
of
the pressure distribution
to
the y-axis
no
resulting resisting force
is
produced either. As this result
is
contradictory to our experience (d'Alambert's paradox), this investigation shows
clearly the significance
of
the viscosity terms in the basic equations
of
fluid
mechanics. When these terms are
not
considered/included in fluidtechnical
considerations for obtaining relevant information with regard
to
fluid physics,
fluid forces
on
bodies can only be dealt with
to
some extent.
FLOW
AROUND
A
CYLINDER
WITH
CIRCULATION
When repeating the procedure where the complex potential
of
two potential
flows were added, in order
to
obtain after determining a free parameter, the
strength
D
of
the dipole current flow, the potential flow around a cylinder, one
can e.g. state the following complex potential:
(
R2)
T
F(z)=U
o
z
+-
+_l_lnz
+Ci.
z
21t
This complex potential results from the summation
of
the potential
of
the
flow around cylinder
and
the potential vortex, where the centres
of
both
flows
lie in the origin
of
the coordinates.
The
constant C was included in the above
equation
to
be
able
to
choose the quantity
of
the stream function again in a
way that
'¥
= 0 when r = R i.e. the outer cylinder
is
to
represent the flow line
'¥
= 0 in the final relation.
For
determining now the constant C we insert in the
above equation
z =
re(icp)
F(z
)=uo(re(/q» +
R2
e(-iq»
+i£ln(re(iq»))+Ci,
r
21t
Making use
of
the relation
eiq>
= cos
<p
+ i sin
<p
it results:
F(z)
=uo[(r
+
~2
)oOS'l' + ;
(r
-
~2
)sin 'I'
]-
~n
'1'+;
~n
Inr
+C"
from which follow the relations for the potential
and
stream function:
(
R2)
r
<1>(r,<p)=U
o
r+-
cos<p--<p
r
21t
(
R2)
r
q'(r,<p)=U
o
r
--
sin<p+-Inr
+C
r
21t
and
In
order
to
obtain
q'
= 0 for r = R and all
<p
one has to choose the constant
C
= -(
~)
In
R Thus results for the complex potential
of
the flow around a
cylinder with circulation:
(
R2)
r z
F
(z
) = U 0 z + - +
i-In
-.
z
21t
R
Potential Flows
267
This potential describes the even flow parallel to the x-axis, in connection
with a dipole current flow
and
a potential vortex located in the origin
of
the
coordinate system.
For
this flow the potential
and
stream function can be stated
as follows:
<I>
(r,
<j»
= U 0 (r + R 2
)COS<j>
_~<j>.
r
21t
'l'(r,<j»=uo(r -
R2)Sin<j>+~ln~.
r
21t
R
iy
X
z
iy
Xz
iy
X
z
(al
(b)
(c)
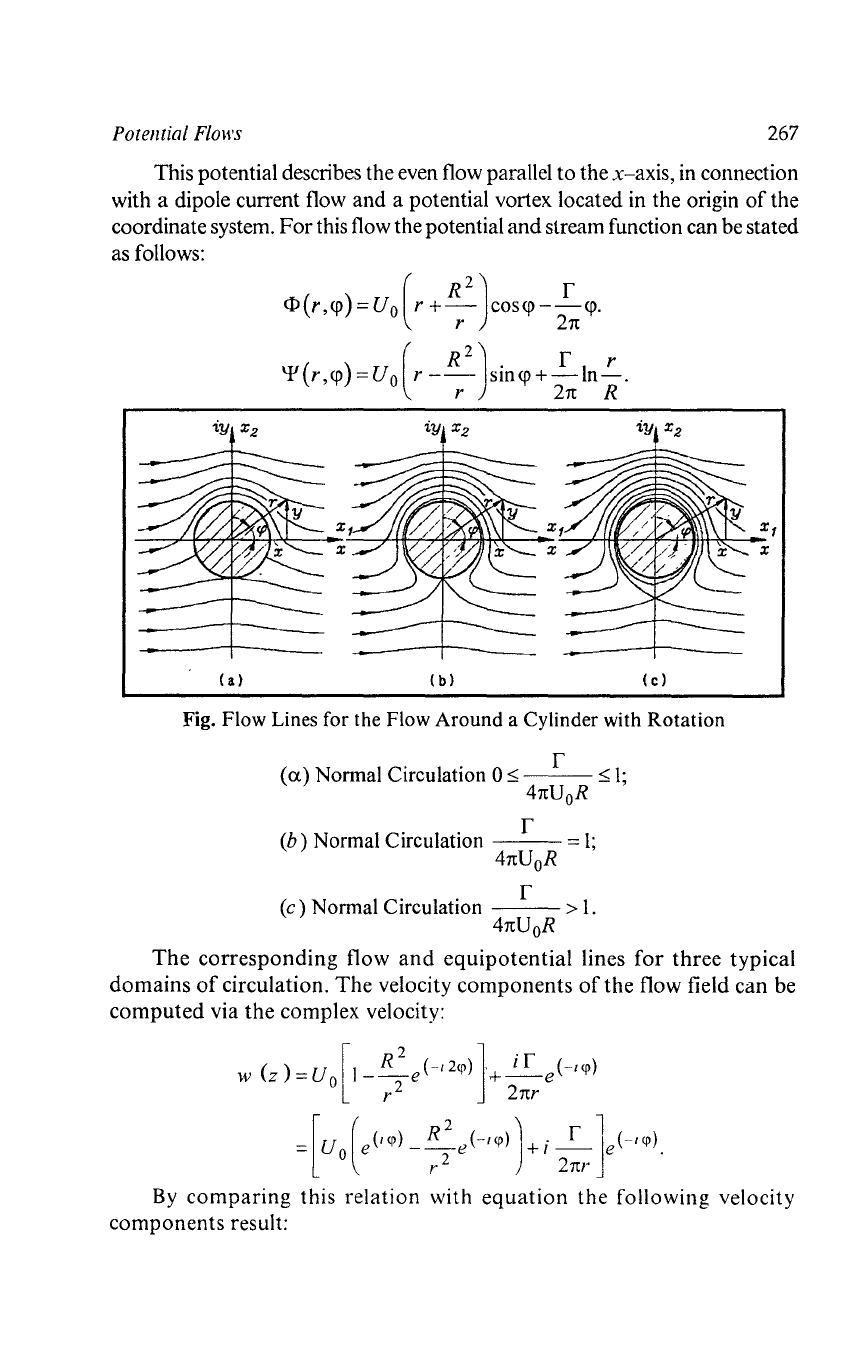
Fig. Flow Lines for the Flow Around a Cylinder with Rotation
(a)
Normal Circulation 0 s r s
I;
41tU
o
R
(b)
Normal Circulation r =
1;
41tU
o
R
(c)
Normal Circulation r >
l.
41tU
o
R
The
corresponding
flow
and
equipotential
lines
for
three
typical
domains
of
circulation.
The
velocity
components
of
the
flow field
can
be
computed
via
the
complex velocity:
(
)
-U
[1
R2
(-121p)],
ir
(-lip)
w Z - 0
--e
+--e
r2
21tr
-[u
((l~~)
R2
(-llp))+.
r
lJ
(-lip)
- 0 e
--e
/-
e .
r 2
21tr
By
comparing
this
relation
with
equation
the
following velocity
components
result:

268
Potential Flows
U
r
=UO(l+ R:)cosq>
and
UIfJ
=-UO(l+
R:)sinq>-~.
r r 2nr
For r = 0 the equations stated result for the potential flow around a
cylinder
withouJ circulation.
When setting
in
the r = R,
in
the above relation, one obtains the velocity
components
U
r
and
UIfJ
along the circumferential area
of
the cylinder:
U
r
=0
afid
UIfJ
=-2Uosinq>-~.
2nR,
As was to be expected, the flow line
\{1
= 0 fulfils the boundary condition
used with solid/body boundaries for the solution
of
Euler's equation. The
Ur.p-
component
of
the velocity has finite values along the cylinder surface.
However, a stagnation point forms in which
Ur.p
=
0;
these are the stagnation
points
of
the flow whose position
on
the outer cylinder area is obtained from
equation for
UIfJ
=
o.
Here the position on the outer cylinder surface
is
only
given for G
£ 4pU
o
R For r = 0 the stagnation points are located at
<j>s
= 0 and
n, d.h. i.e. on the x-axis. For finite r
-values
in the range
of
0 < r
/(
4nUoR)
< 1
<j>s
is
computed as negative, so that the stagnation points come to lie
in
the
third and fourth quadrant
of
the cylinder area. For r /(4nU
o
R) = 1 the
stagnation points
is
located
ill
the lower vertex
of
the outer cylinder area: for
n 3
this value
q>s
=
--
is
computed and
-.
2 2n
When the circulation
of
the flow
is
increased further, so that
r>
(4nU
o
R) holds, the stagnation point
of
the flow cannot form any more along the
outer cylinder area; the formation
of
a "free stagnation point"
in
the flow field
comes about. The position
of
this point for U
r
= 0 and
Ur.p
= 0 can be computed
from the above equations for the velocity components, i.e. from:
Uo(I<:}OS~,
~O
and
U
O
(l+
R2)sinq>s
=_~.
r;
2nrs
As
rs
"#
R, i.e.
the
formation
of
the
free
stagnation
point
on
the
circumferential area is excluded, the first
of
the above two equations can only
n 3
be fulfilled for
q>s
= -
or
-2
Thus the second conditional equation for the
2 n
position coordinate
of
the "free stagnation point" reads:
UO(l+
R2)=+~
r;
2nrs

Potential Flows 269
As
r>
0 can be assumed
in
the above equation, and as the left side
of
the
equation can only adopt positive values, only the positive sign
of
the above
equation with the requirements concerning the flow yields consistent values,
i.e. the conditional equation for
rs
reads:
Uo(l+~)=~
r}
21trs
2 I 2
or
transcribed
rs
---rs
+R
=0.
21tU
o
As a solution
of
this equation one obtains:
r
=_1_+
(_r_)2
_R2
s
41tU
o
-
41tU
o
.
With this the position coordinates
of
the free stagnation point result as:
=
37t
and
rs
= I
[1
+
1_(41tU
oR)2].
CPs
2 R 41tU
oR
I
The negative sign
of
the root
in
the solution for
rs
was omitted
in
the
statement
of
the position coordinates for the free stagnation point, as this would
lead to a radius which is located within the outer cylinder area. As only the
flow around the cylinder
is
of
concern, this second solution
of
the square
equation for
rs
holds no interest.
Moreover, it was also excluded from the solution for the position
coordinates
of
the free stagnation point that the angle
CPs
has also a solution
1t I
for
"2
The reason for this lies
in
the fact that for
41tU
oR
= 1 the stagnation
point appears as a solution only
in
the lower vertex
of
the outer cylinder area.
1t
An inclusion
of
the solution for
CPs
="2
would mean that a small increase
of
the circulation, to an extent that the standardized circulation
is
given a value
larger than
1,
would lead to a
jump
of
the stagnation point from the lower to
the upper vertex. Considerations on the stability
ofthe
position
of
the stagnation
31t
points show, however, 'hat only the lower stagnation point, i.e
CPs
= 2
can exist as a stable solution. Because
of
the superposition
of
the flow around
a cylinder with a potential vortex a flow field has come about, which again
is
symmetrical concerning the y-axis. With this
it
is
in tum determined that owing
to the flow the outer cylinder area obtains no resulting force acting in flow
direction, i.e. no resisting force occurs because
of
the flow. Owing to the
circulation
an
asymmetrical
flow
in
relation
to
the
x-axis
has
come

270
Potential Flows
about,however, and this leads to a buoyancy, i.e. to a resulting force on the
cylinder, directed upwards. As the velocity component on the upper side
of
the cylinder
is
larger than on the underside, because
of
the Bernoulli equation
an excess pressure results prevailing on the underside, which causes a flow
force directed upwards. The quantitative determination
of
this force requires
integral relations.
SUMMARY
OF
IMPORTANT
POTENTIAL
FLOWS
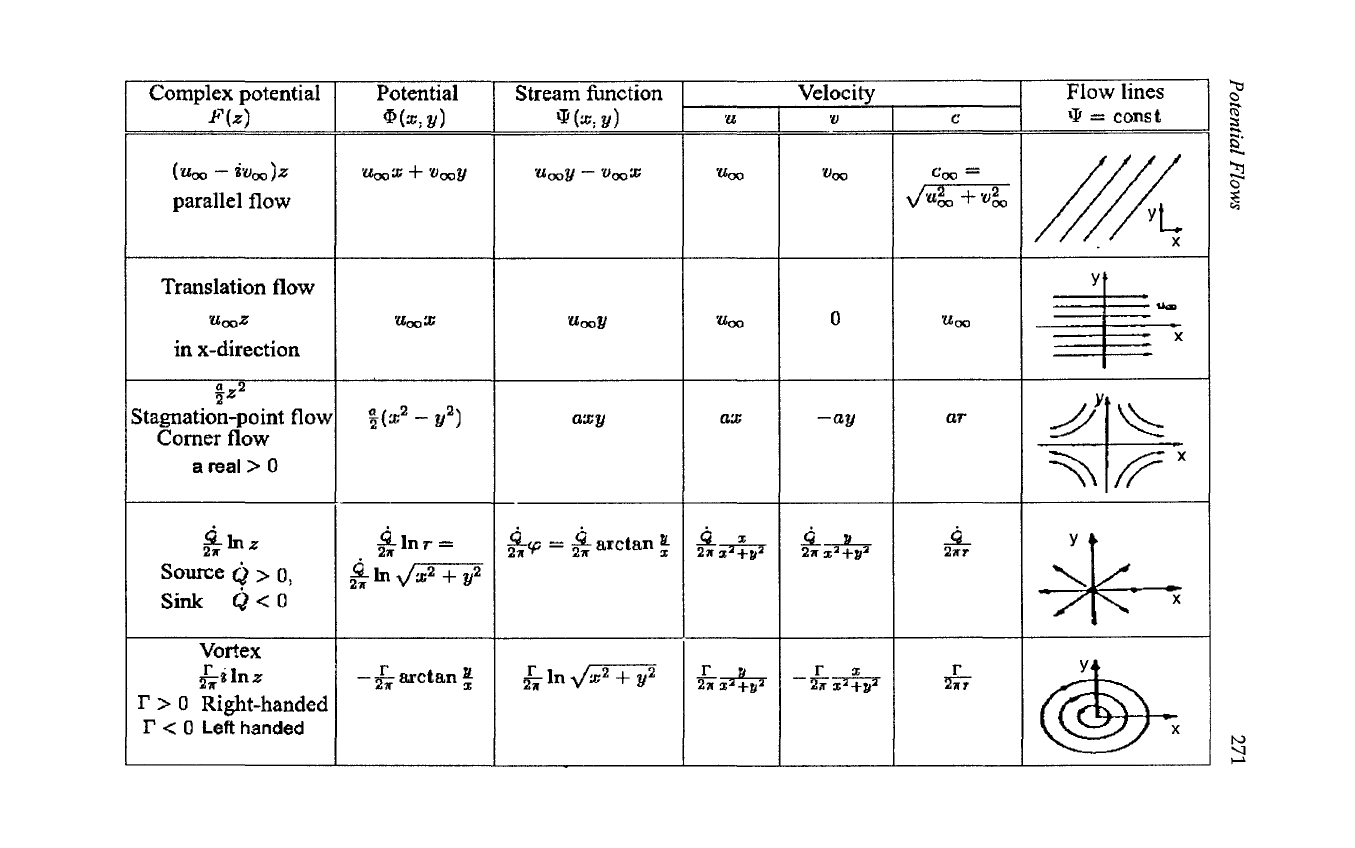
In
the preceding representations a number
of
potential flows was discussed
which are known as basic flows and whose treatment gives an insight into the
occurring flow processes.
In
the following table further analytical functions
are stated,
in
addition to the already extensively discussed examples, which
can
be
used for the derivation
of
potential and stream functions and the
corresponding velocity fields
of
potential flows. By equating the indicated
potential or stream-function values to a constant, the equipotential or flow
lines
of
the potential flow can be stated. The procedure concerning the
derivations
of
fluid-mechanically interesting quantities shall be represented
her once gain briefly with the aid
of
the sourcesink flow taken from the table.
. .
Example:
F
(z
) =
~
.In z =
~
(In r + i
<p);
z = x + iy =
re
i
<jl
2n 2n
<l>
=
~
In
r =
~
In
~
x 2 + Y 2
2n
2n
Potential:
S
f
'·
\TIQ
Q t
Y
tream unctIon: T
=-<p=-arc
an-
2n 2n x
Velocity:
a<l>
Q x a'I'
u=-=
=-
ax
2n x 2 + Y 2
ay
a<l>
Q y a'I'
u---
=
-
ay
- 2n x 2 + Y 2
ax
Equipotential lines:
~
2n
2
y =
e--;-.K<l>-x
<p=K
<I>
Stream Lines: Y
=X
tan(~n
JK'P
'I'=K
'P
Q
Complex potential Potential Stream function
Velocity
Flow lines
P(z)
cI>(:c,y)
1J!(:c,
y)
'U
'l)
C
\Ii
= const
(u
oo
- i'l)oo)z
uoo:c + vooy
uooy-voo:c
'U
oo
'l)oo
Coo
=
~
parallel flow
J'u
2
+'l)2
00 00
. x
Translation flow
..
UooZ
uoo:c 'uooy
U
oo
0
U
oo
in
x-direction
~z2
~r~
Stagnation-point flow
~(:c2
_ y2)
a:cy
a:c
-ay
aT
Corner flow
a
real> 0
~
;?x
&'lnz
~lnT=
SLcp
=
SL
arctan
fL
SL
x
SL--1L-
~
*-'
211'
2-x
211'
x
211'
X
2
+fJ2
211'
X
2
+fJ2
211'r
Source Q >
0,
~ln
J:c
2
+
y2
Sink
Q < 0
Vortex
rl
-
f,;:
arctan
1L
Ji-In
J:c
2
+ y2
i: X
2
!fJ2
r x
r
~
21ft
nz
II'
x
-2/1' X
2
+fJ2
"2iT
r > 0 Right-handed
r < 0 Left handed
