Brewster H.D. Fluid Mechanics
Подождите немного. Документ загружается.


202
Integral Forms
of
the Basic Equations
C dotT
ap
+c
T
a(pU;)
0
u
at
u ax.
I
one obtains the initial equation for the derivation
of
the integral form
of
the
thermal energy equation:
a(pcuT) a (pcuTU
j
) _
aq;
au; aU
j
--'-----'-'--'-+
-----p---'tij
--.
at
aX
I
ax;
ax;
ax;
With cvT = e (inner energy) one obtains:
a(pe)
a(peu;)
aq;
au;
aU
j
--+
=----p---'tij
--.
at
ax; ax; ax; ax;
The integration
of
equation over a control volume yields:
f a(pe) dV + f
a(peu;)
dV
=-
f
aql
dV
V
at
v
ax
i
v
aXi
KKK
J
au·
J aU
j
"(")
- p
__
1 dV -
'tij
--dV
+
L...J
Q +E .
v
K
ax; v
K
ax;
Transcribed, in consideration
of
Gauss'
integral theorem
and
the
reversibility
of
the sequence
of
integration and differentiation, one obtains:
! ( J pe
dV)+
J peU
i
<iF;
=-
J
qi<iF;
v
K
OK
OK
,
,~
'---v---'
i
11
ill
- J
p.
au;
dV
-
J'tij
pU
j
dV
+ L(Q+E).
vax;
0 ax;
~
,K
v
"K
v ' VI
IV V
The terms
of
the resulting equation can be interpreted as follows:
I:
Temporal change
of
the inner energy within the control volume
V
K
•
II:
Convective outflow and inflow
of
inner energy per time unit over
the surface
OK
of
the control volume.
III: Molecular heat flow per time unit, i.e. the sum
of
the outflow
and inflow,
over the surface
OK
of
the control volume.
N:
The work done during expansion
by
the total volume per time
unit
V:
The mechanical energy dissipated per time unit in the total volume
VI: External heat and energy flow per time unit which is supplied to
the total volume

Integral Forms
of
the Basic Equations 203
The above equation holds likewise for an ideal fluid, but term IV is equal
to zero, as no work can be done during expansion because
of
p = const.
APPLICATIONS
OF
THE
INTEGRAL
FORM
OF
THE
BASIC
EQUATIONS
The importance
of
the integral forms
of
the basic equations
of
flow
mechanics becomes clear from applications that are listed below. Many
manuals on the basics
of
flow mechanics treat flow problems
of
this kind.
Typical examples are treated that make clear that the derived integral form
of
the basic equations represent the basis for a variety
of
problem solutions, where
attention has to be paid to that solutions often can be derived only by employing
simplifications.
Reference
is made to these
simplifications
and
their
implications for the obtained solutions in the framework
of
the derivations.
In order to introduce the reader into the methodically correct handling
of
the integral form
of
the equations, each
of
the problems treated below is solved
by starting from the employed basic equation in each case. Then those terms
in the integral form
of
the used basic equation are deleted which are equal to
zero for the treated problem. In addition, by introducing simplifications terms
are removed which have very little influence on the treated problem, so that
easily comprehensible solutions are obtained.
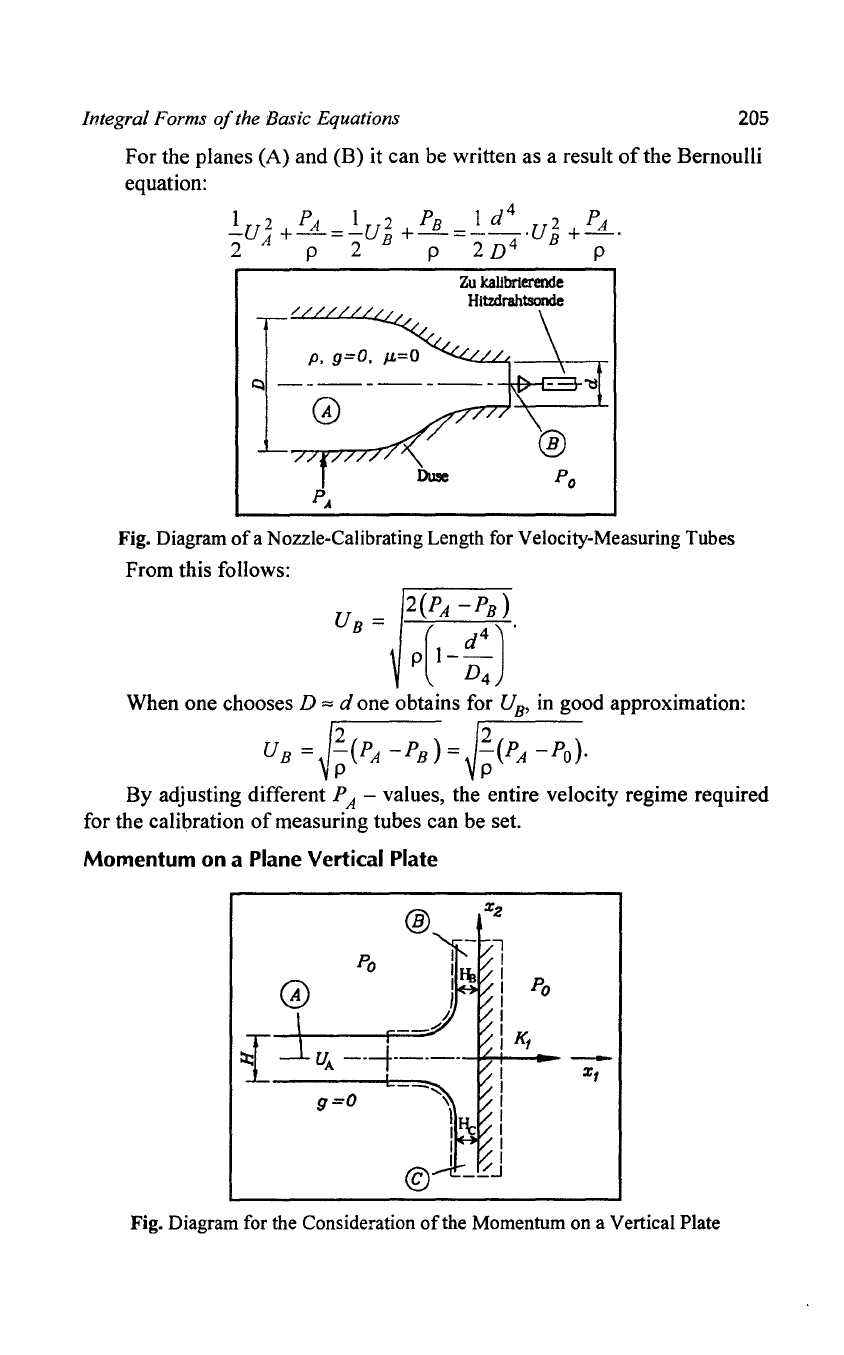
Outflow from Containers
.--
______
-;Ausstromoffnung
T
H
1
Fig. Diagram
for
the
Treatment
of
Outflows
from
Containers
In Figure a simple container is sketched, having the diameter D, which is
partly filled with a fluid and is assumed to be closed at the top. Between the
fluid surface and the container lid there is a gas having the pressure
PH'
The fluid height is H and at the bottom
of
the container there is an opening
with the diameter d. Sought is the outflow velocity from the container, i.e. the
velocity U
d
.

204
Integral Forms
a/the
Basic Equations
From the opposite diagram, i.e. from Figure it can be seen that the water
surface is moving downwards with the velocity
U
D
.
because
of
the fluid flowing
out, which exits with U
d
from the exhaust/escape opening. Via the integral
form
of
the continuity equation holds:
--
1t21t2rn2
pUF
=const-pU
D
-D
=pU
d
-d
- U
D
=-2
U
d
·
4 4 D
By
employment
of
the Bernoulli equation between the points (A) and
(B) one obtains:
1 2
PH
1 2
Po
-U
D
+-+gH
=-U
d
+-.
2 p 2 P
Thus it results:
1 2 1 2
1(
)
-U
d
=-U
D
+gH
+-
PH
-Po,
2 2 P
or
after insertion of:
1
2 1
[d
4
)
2 1 ( )
-U
d
=-
- U
d
+gH
+-
PH
-Po,
2 2 D4 P
1 2 1
[d
4
)
2 1 ( )
-U
d
=-
- U
d
+gH
+-
PH
-Po,
2 2 D4 P
2
2gH
+-(P
H
-po)
p
Exit Velocity from Nozzles
In flow mechanics it is necessary to calibrate indirectly working measuring
processes (stagnation-pressure tubes, hot-wire anemometry etc.) in flow fields
in which the flow velocity is known.
By
letting flows stream into nozzles it
can be achieved that at the nozzle exit the flow velocity required for calibration
can be adjusted via the pressure in the input pipe
of
the nozzle.
The integral form
ofthe
continuity equation holds in the following form:
.
-UrI;"
U
1t
D
2 U
1td2
m = p r = const - p A - = P B - ,
4 4
i.e. one can write for U
A:
Integral Forms
o/the
Basic Equations
205
For the planes (A) and (B) it can be written as a result
of
the Bernoulli
equation:
1 2 P
A
1 2 P
B
1 d
4
2 P
A
-UA
+-=-U
B
+-=--,U
B
+-.
2 P 2 P 2 D4 P
Zu
kaUbrierende
Hitzdrahtsonde
Fig. Diagram
ofa
Nozzle-Calibrating Length for Velocity-Measuring Tubes
From this follows:
2(P
A
-P
B
}
P(l-~J
When one chooses D
:::::
d one obtains for U
B
,
in
good approximation:
U
B
=
f3..(P
A
-P
B
}=J3..(P
A
-po}·
~p
P
By adjusting different P A - values, the entire velocity regime required
for the calibration
of
measuring tubes can be set.
Momentum on a Plane Vertical Plate
®
{-I::==....
g=O
©
:-j
I
I
I
Po
I
I
IRt
Fig. Diagram for the Consideration
of
the Momentum on a Vertical Plate
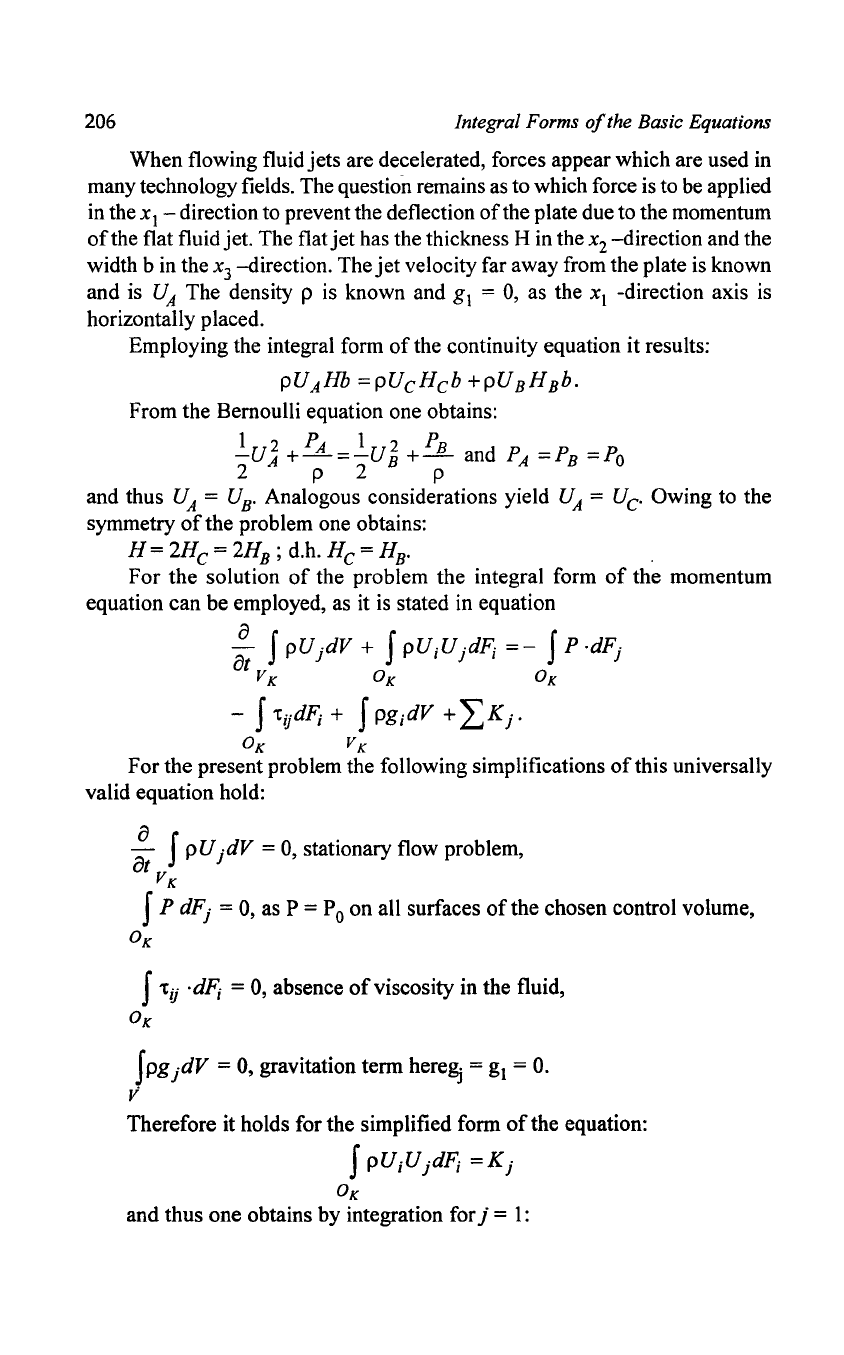
206
Integral Forms
of
the Basic Equations
When flowing fluid
jets
are decelerated, forces appear which are used in
many technology fields. The question remains as to which force is to be applied
in the
xl
- direction to prevent the deflection
of
the plate due to the momentum
of
the flat fluid jet. The flat
jet
has the thickness H in the x
2
-direction and the
width b in the
x3
-direction. The
jet
velocity far away from the plate is known
and is
U
A
The density p is known and g I =
0,
as the
xl
-direction axis
is
horizontally placed.
Employing the integral form
of
the continuity equation
it
results:
pUAHh
=pUeHeh+pUBHBh.
From the Bernoulli equation one obtains:
1
2 P
A
1 2 P
B
-UA
+-=-U
B
+-
and P
A
=P
B
=P
o
2 P 2 P
and thus U
A
=
UB.
Analogous considerations yield U
A
=
Uc-
Owing to the
symmetry
of
the problem one obtains:
H = 2He =
2HB
; d.h. He = H
B
. .
For
the
solution
of
the problem the integral form
of
the momentum
equation can be employed, as it
is
stated in equation
~
r pU .dV + r
pU·U
.dF
=-
r P ·dF-
atJ
1
Jill
J }
V
K
OK
OK
-
ftifdF;+
fpgjdv+LK
j
.
OK
v
K
For the present problem the following simplifications
of
this universally
valid equation hold:
~
f
pU
jdV
= 0, stationary flow problem,
at
v
K
f P dF
j
= 0, as P =
Po
on all surfaces
of
the chosen control volume,
OK
f
tif
·dF;
= 0, absence
of
viscosity in the fluid,
OK
f pg
jdV
= 0, gravitation term
here~
= gI = 0.
v
Therefore it holds for the simplified form
of
the equation:
f pUjUjdF;
=K
j
OK
and thus one obtains
by
integration for j =
1:
Integral Forms
of
the Basic Equations
207
Kl
=-pU'iHB.
The result
of
the above derivations shows that K
1
•
must act in the negative
xl
-direction, in order to prevent the deflection
of
the plane plate by the
incoming flat fluid jet. This gives an example
of
which kind the force terms
are
~
that occur in equation. All forces are included that act on the considered
control volume.
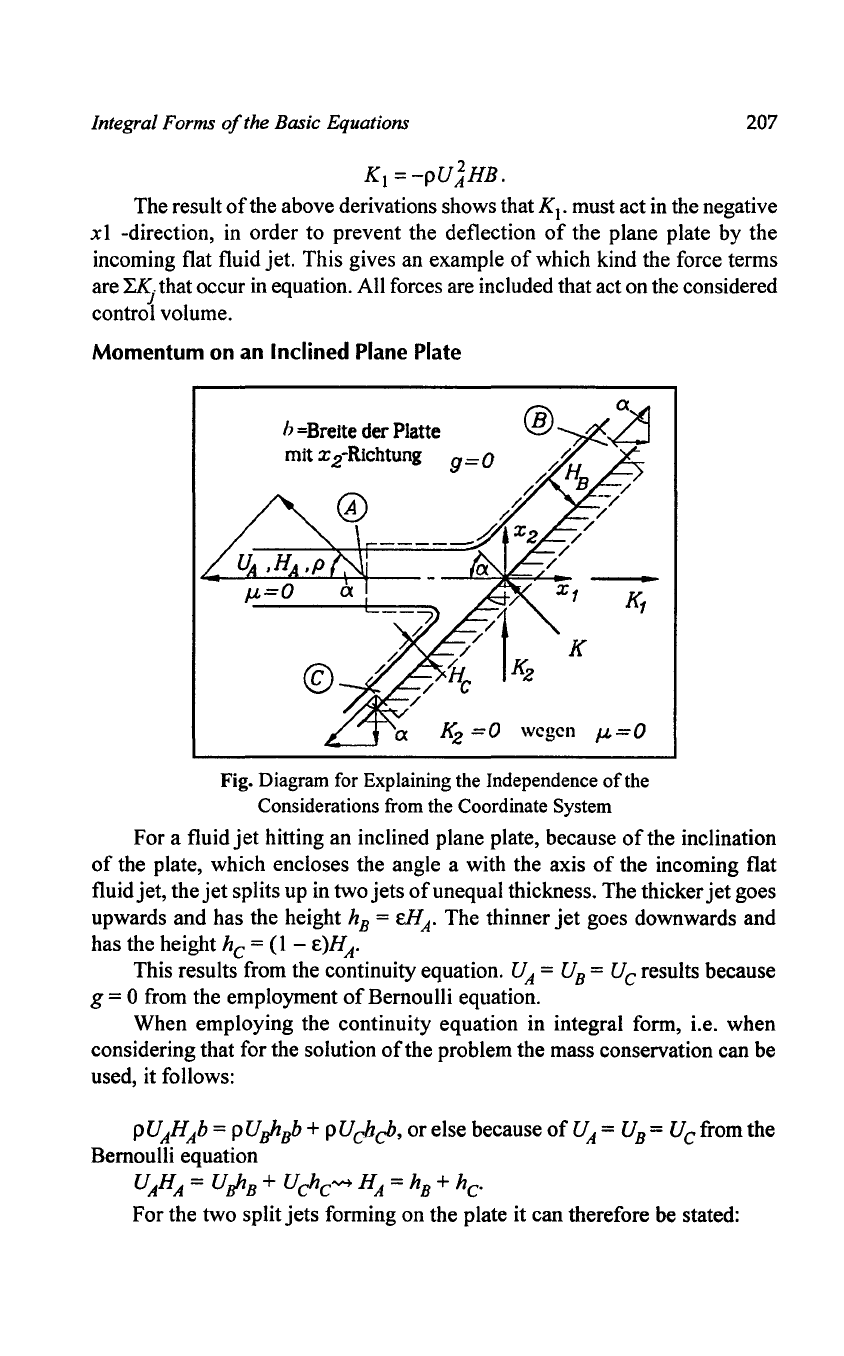
Momentum on an Inclined Plane Plate
h
=Brelte
der
Platte
mit
x 2-Richtung g = a
~
=0
wcgcl1
f.L
=0
Fig. Diagram for Explaining the Independence
of
the
Considerations from the Coordinate
System
For a fluid
jet
hitting an inclined plane plate, because
of
the inclination
of
the plate, which encloses the angle a with the axis
of
the incoming flat
fluid jet, the
jet
splits up in two jets
of
unequal thickness. The thicker
jet
goes
upwards and has the height
hB
=
EllA'
The thinner
jet
goes downwards and
has the height
he
=
(1
-
E)H
A
.
This results from the continuity equation. U
A
= U
B
= U
e
results because
g = 0 from the employment
of
Bernoulli equation.
When employing the continuity equation in integral form, i.e. when
considering that for the solution
of
the problem the mass conservation can be
used, it follows:
pUAHAb
=
pUshB
b
+ pUchch, or else because
of
U
A
= U
B
= U
e
from the
Bernoulli equation
UAH
A
=
UshB
+
Uche-
HA
=
hB
+ he'
For the two split
jets
forming
on
the plate it can therefore be stated:

208
Integral Forms
of
the Basic Equations
hB
=
EllA
and
he
=
(1
-
E)H
A
·
When one employs the integral momentum equation:
~
fpU.dV
+
fpU.U.dF
=-
f
PdF
.
at
J
IJI
J
V
K
OK
OK
- f'tijdF;+
fpgjdV+LKj'
OK
V
K
the following simplifications can be introduced:
: f
pUjdV
= 0, stationary problem,
t V
K
f P
dF
j
= 0, as P = Po on all surfaces
of
the chosen control volume,
OK
f
'tijdF;
=
0,
viscosity-free fluid,
OK
f
pgjdV
= 0, insignificant term
or
gj
= °
v
K
For
the simplified form
of
the above integral momentum equation thus
holds:
f pUjUjdF;
=K
j
.
OK
When one chooses a coordinate system oriented by the plate, then for K
result by integration over the planes (A), (B) and (C) three contributions which
are stated below:
Kp
=-pU'jHAb
sinu+pU'jEHAb
-pU'j
(I-E)HAb.
As in the present problem
Il
= ° was set, for the force
Kp
= 0. acting
along
the plate attacked by flow, From this results from equation
or
one obtains for
E:
-1-sinu+2E
=0,
E·=
.!.(l + sin
a).
2
For
the force acting vertically to the plate it is computed
Ks:
K s = pU'j H A b cos
u.
It
is
evident
that
the
considerations
carried
out
above
have
to
be
Integral Forms
of
the Basic Equations
209
independent from the chosen coordinate system. When
one
chooses
the
coordinate
system
one obtains for
Kl
the
below-stated contributions
by
integration over the planes (A), (B) and (C):
Kl
=-pU'jHAb
+pU'jeHAb
sina-pU'j
(I-&)HAb
sina.
For the-force
K2
yields:
K2 = pU'jEHAb
cosa-pU'j
(l-&)HAb
sina.
As because
of
J..L
= 0 the total force
on
the plate K resulting from
Kl
and
K2
has to
act
on the plate vertically, it holds:
K sin a K 2 2 E cos a -
cosa
tan a = = =
------
-Kl
K
cosa
1-2Esina+sina
From this
-it
is computed 2£ cos
2
a - cos
2
a = sin
a.
- 2£ sin
2
a.
+ sin
2
a.
or
for
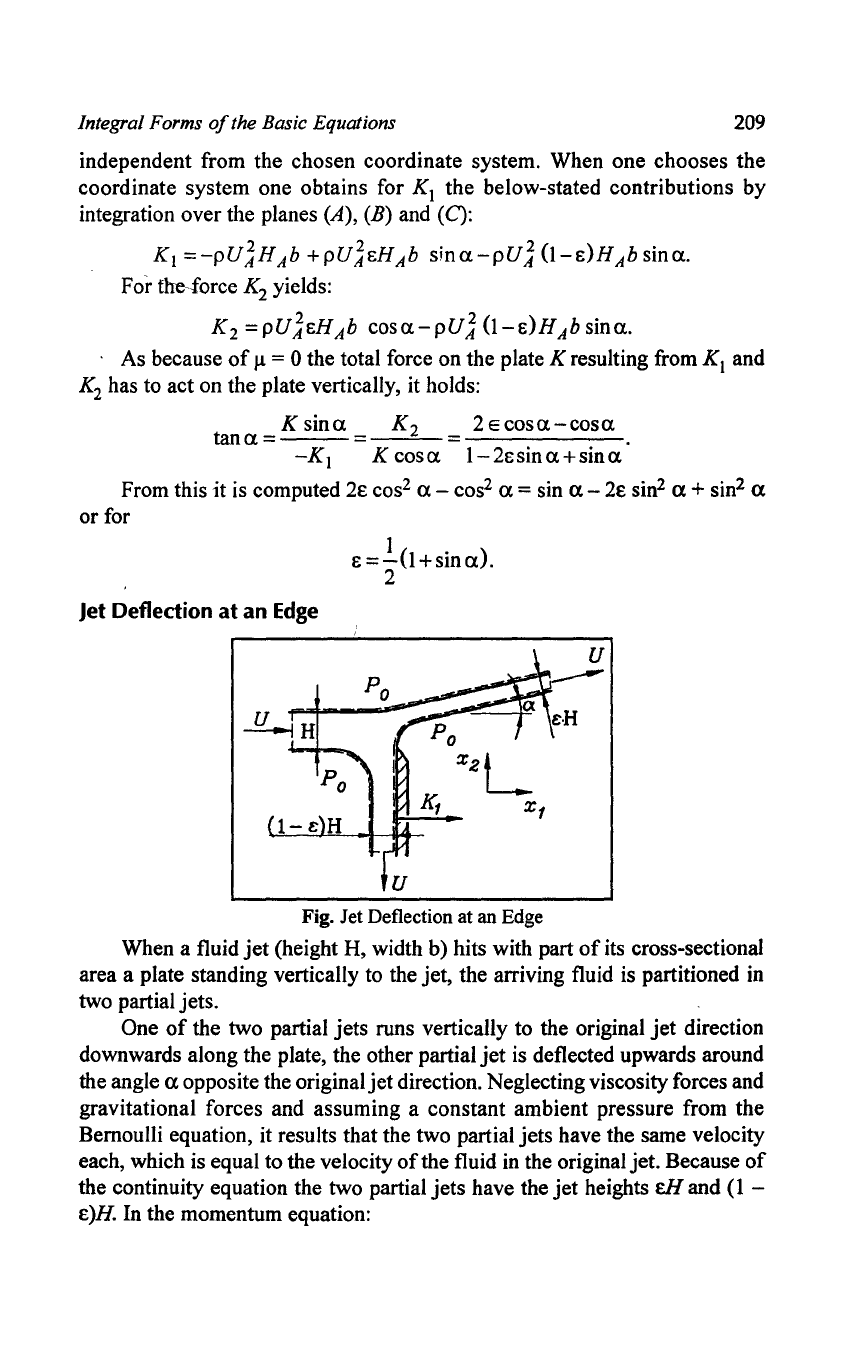
Jet
Deflection at
an
Edge
~H
E = .!.(l + sin
a).
2
Fig. Jet Deflection at an Edge
When a fluid
jet
(height H, width b) hits with part
of
its cross-sectional
area a plate standing vertically to the
jet,
the arriving fluid is partitioned in
two partial
jets.
One
of
the two partial
jets
runs vertically to the original
jet
direction
downwards along the plate, the other partial
jet
is deflected upwards around
the angle
a.
opposite the original
jet
direction. Neglecting viscosity forces and
gravitational forces and assuming a
constant
ambient pressure from
the
Bernoulli equation, it results that the two partial
jets
have the same velocity
each, which is equal to the velocity
of
the fluid in the original
jet.
Because
of
the continuity equation the two partial
jets
have the
jet
heights
Elf
and
(1
-
£)H.
In the momentum equation:

210
Integral Forms
a/the
Basic Equations
~
JPU
·dV
+ J
pU·U
·dF
=
at
) , ) ,
V
K
OK
-
JPdF
j
-
J'tijdF
j
+
JpgjdV+LKj
OK
OK
V
K
the following simplifications can be made:
: J
pUjdV
= 0, stationary problem,
t v
K
J P
dF
j
= 0, constant pressure along the surface
of
the control volume,
OK
J
'tij
dF;
=
0,
viscosity forces are neglected,
OK
J
pg
jdV
= 0, gravitation is neglected
..
OK
It results the following simplified momentum equation:
J
pUjUjdF;
=
LK
j
.
OK
The force exerted on the fluid can be determined by the equation for the
xl
- components.
-pUU
(bH)+p(U
cosa)U
(ebH)
=K
1
.
Kl
=-pU
2
bH(1-ecosa)
The negative value
of
the force
Kl
results from the fact that the force
exerted
on
the plate is computed.
From the equation
for
K2
pU(l-E)Hb(-U)
+ pUEbH(Usin
a)=
0, results for
K2
= ° the connection
between the deflection angle
a and the ratio
E:
-pU
2
bH
[(1
- E)
~
E sin
a]
= 0,
1
e=---
l+sina
Thus the splitting up
of
the
jet
in can be determined from the deflection
of
the
jet
from the horizontal position, i.e. by measuring the angle
a.
Mixing Process in a Pipe of Constant Cross-section
In a pipe two flows
at
a constant velocity
(U
A
'
UB)' each are mixed with

Integral Forms
of
the Basic Equations
211
one
another(~
= 0). The pressure at point 1 and the partial areas
(U
A
,
UB).
and
A
B
.
shall
be
given. Sought is the pressure
Plat
point 2 where a constant velocity
U c . over the pipe cross-section has set-in.
Fig. Diagram for Explaining the Mixing Process
From the integral form
of
the continuity equation one obtains:
b(-pHAU
A
-pHBU
B
+P(H
A
+HB
)U
c
)=0,
or
rearranged for U c :
-
UAHA+UBH
B
U C =
~~~--=--
HA
+HB
The momentum equation
~
f
pU
·dV
+ f
pU·U
·dF
=-
f PdF-
at
J
IJI
}
V
K
OK
OK
-f 'tijdF; + f pgi
dV
+
L,K
j.
OK
V
K
can be simplified as follows:
: f
pUjdV
= 0, stationary flow problem,
t v
K
f 'tijdF; =
O,~
= 0, i.e. the assumption
of
absence
of
viscosity,
OK
f
pg
jdV
= 0, no component
of
gravitation in horizontal direction,
v
K
L,K
j = 0, no external forces act on the control volume.
From this follows:
f
pUiUjdFf
=-
f
PdF
j
.
OK
OK
For the present problem this results in:
