Brewster H.D. Fluid Mechanics
Подождите немного. Документ загружается.


172
Hydrostatics and Aerostatics
carried out here
is
the swface tension. This surface tension can be proven by
immersing a strap, in a fluid. When pulling the strap through the free swface
upwards, one observes that this requires an action offorces which
is
proportional
to the distance between the strap arms. The proportionality constant describing
this fact
is
defined
as
swface constant.
The
surface tension represents thus
an action
of
forces
of
the free surface per unit linear measure.
It
can also
be introduced as the energy that
is
required to build up the tension in the
liquid film in figure. Both introductions are identical as in
both
types
of
energy equation formulated in this way the length
of
the liquid film in the
direction in which the strap
is
pulled
is
introduced from the energy set-
up. This makes it clear
that
both possibilities
of
introduction
of
the surface
tension, one as the action
of
forces per unit linear measure and other as
the energy
per
unit area, are identical.
In concluding these
introductory
considerations
the
effect
of
the
surface tension
on
the
areas above
and
below a free surface shall be
investigated.
From
observations
of
free surfaces in the middle
of
large
containers one can infer
that
the surface tension there has
no
influence
on
the fluid
and
the gas area lying above it, as the free surface forms vertically
to the field
of
gravity
of
the earth, as stated in Figure.
From
this, it follows
that
considerations
of
fluids with free surfaces can be carried
out
far away
from fluid boundaries (container walls) without consideration
of
the wall
effects. When one considers a curved surface element, one understands
that
as a consequence
of
the occurring surface tensions actions
of
forces
are directed to the side
of
the surface
on
which the centre points
of
the
"circles
of
curvature" are located.
The
forces attacking
on
sides
AD
and
Be
of
the surface element are computed for each element dsl and the action
offorces resulting from them in direction
of
the centre points
of
the circles
of
curvature
is:
cr
cr
dK
=
-ds}
ds
2
=-dO
I
R2
R}
Accordingly the action offorces
dK
2
is
computed as
cr cr
dK
=
-ds
2
ds}
=
-dO
2
R2 R2
This shows that as a consequence
of
the surface tension pressure effects
occur that are directed (in direction of) towards the centre points
of
the circles
of
curvature. This pressure effect
is
computed
as
force per unit area, i.e. a
differential pressure
that
is
caused by the surface tension:

Hydrostatics and Aerostatics
h---
0---
----
r
-d
--
....+....-L-"':""- 0
-=-
~
p
--
- - - -
gb--=--_
---
p---
------
g---
--------
Fig. Diagram for the Consideration
of
Pressure in Bubbles
When there
is
a spherical surface it holds
20'
R} =
R2
=
~
I1pcr
=R'
173
This relation means
that
the gas pressure in a spherical bubble
is
larger
than
the fluid pressure imposed from outside:
20'
PF+
R
= P
g
.
For
very small bubbles this pressure difference can be very large.
When one considers the equilibrium state
of
a surface element
of
a bubble,
the following relation can be written for the pressure in the upper apex:
Po
+ PFgho +
0'(
~)
= Pg,o
For
a surface element
of
any height the following pressure equilibrium
holds:
Po
+ P Fg(ho +
y)
+
0'(_1
+
_1_)
= P 0 +
rvy.
Rl
R2
g,
guo
When
one
now forms the difference
of
these pressure relations
one
obtains:
(
1
1)
2 1
-+-
--+-(PF
+pg)gy=O.
Rl
R2 R2
0'
Thus
the characteristic quantity for the standardization
of
equation
is
to
be introduced
174 Hydrostatics and Aerostatics
20'
U=
g(PF
- P
g
) .
which
is
known as Laplace constant
or
capillary constant.
It
has the
dimension
of
a length
and
indicates in orders
of
magnitude when a
perceptible influence
of
the surface tension on the surface shape
of
a
medium exists.
It
holds:
• When the Laplace constant
of
a
free
surface
of
a liquid
is
comparable
with the dimensions
of
the fluid body, an influence
of
the surface
tension on the fluid shape
is
to be expected.
•
In
the proximity
of
fluid rims (container walls) an influence
of
the
surface tension on the shape
of
the "fluid surface"
is
to be expected
in areas that are
of
the order
of
magnitude
of
the Laplace constant.
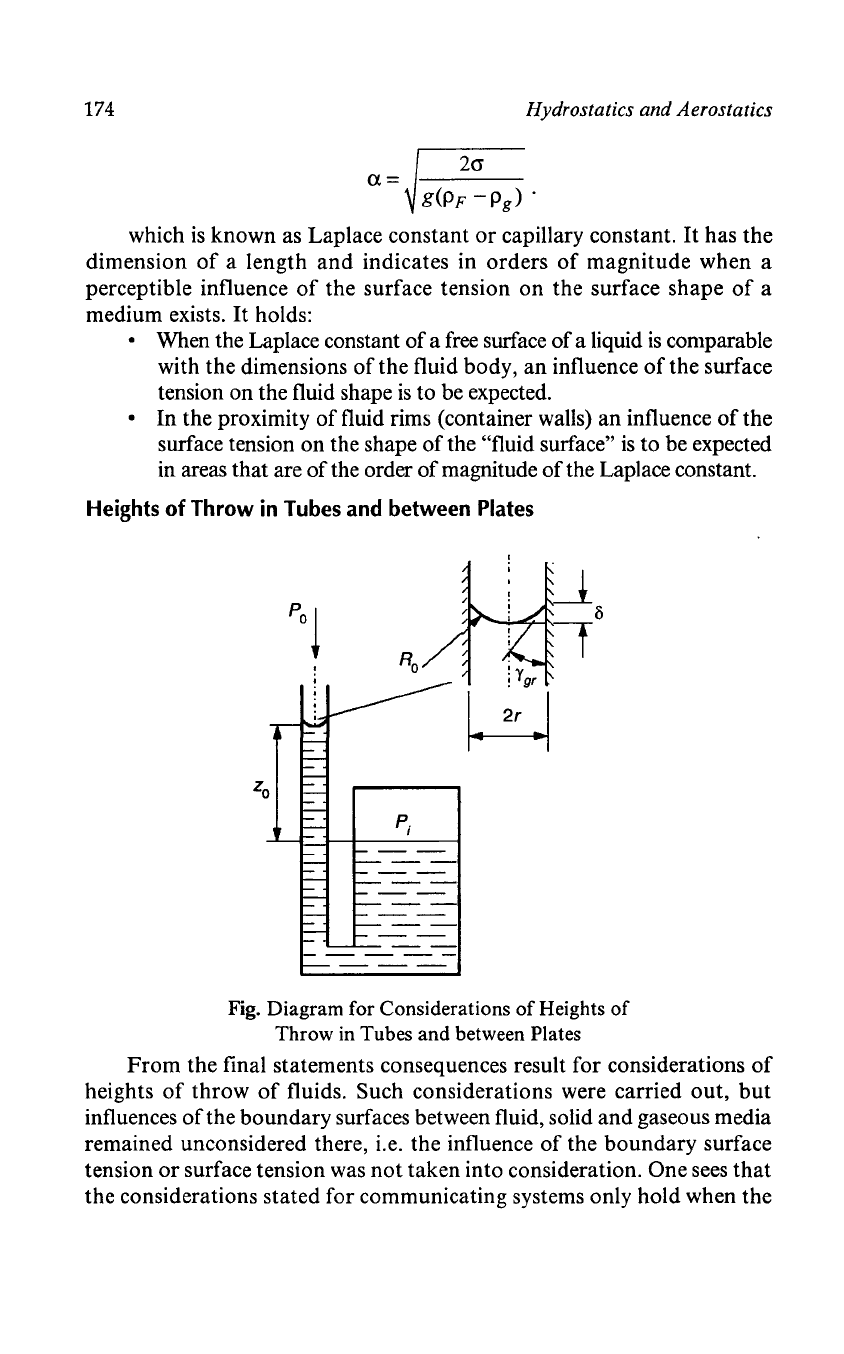
Heights
of Throw
in
Tubes
and
between
Plates
Fig. Diagram for Considerations
of
Heights
of
Throw in Tubes and between Plates
From
the final statements consequences result for considerations
of
heights
of
throw
of
fluids. Such considerations were carried out,
but
influences
of
the boundary surfaces between fluid, solid and gaseous media
remained unconsidered there, i.e. the influence
of
the boundary surface
tension
or
surface tension was
not
taken into consideration. One
sees
that
the considerations stated for communicating systems only hold when the

Hydrostatics and Aerostatics
175
dimensions
of
the systems are larger
than
to
the Laplace constant
of
the
fluid
boundary
surfaces. Moreover,
the
considerations only hold far away
from fluid rims. In the immedi.ate proximity
of
the rim there exists
an
influence
of
the surface tension which remained unheeded.
The
processes taking place in fluid containers
of
small dimensions
can be treated easily when carrying
out
a division
of
the container walls
in as
"wetting"
ones
and
"non-wetting"
ones.
When
making
the
considerations
at
first for wetting walls, experiments show
that
for such
surfaces, in small tubes
and
between plates with small distances/gaps, the
fluid in the tube
or
between the plates assumes a height which
is
above
the height
of
the surface
of
a larger container.
From
equilibrium considerations it follows:
0-
Pressure between plates
Po
-
~
=
PF
= Pi
-PFgzo,
Pressure in tubes
or
in other form:
1
0-
Height
ofthrow
between plates
Zo
=
--(Pi
- Po)
+-n.
'
PFg
PFg~'O
1 20-
Height
of
throw in tube
Zo
=
--
(Pi - Po) +
.-n.
.
PFg
PFg~'O
Here the radius
of
curvature
Ro
is
to be considered as an unknown for the
determination
of
which two possibilities exist.
To
simplify the derivations one
can assume with a precision that
is
sufficient in practice that the surface in the
rising pipe adopts the form
of
a partial sphere for the tube and that
of
a partial
cylinder for the gap
of
plate. The angle
of
contact between fluid surface
and
tube wall
or
plate wall has
to
be known from statements on the possibility
of
wetting. When one defines this angle as
Yo
r
' one obtains the following relation:
r =
Ro
cosY,.
For
the final relation
of
the height
of
tfuow
Zo
for the plates and the tube
thus holds:
Plates
1
0"
Zo
=
--(PI
-
po)+--cosYgn
PFg PFgr
1
20"
Tube Z =
--(PI
-
Po)+--cosYgr'
o PFg PFgr
This final relation now shows
that
even in the case
of
pressure equality,
176
Hydrostatics and Aerostatics
1t
i.e,Pi =
PO'
the
height
of
throw
assumes finite values
ifY
gr
< 2'
This
fact
has
to
be
considered
when
employing
communicating
systems
for
measurements
of
the
height
of
throw
and
when
measuring
pressures.
The
second
possibility
to
compute
the
height
of
pressure
is
given
by
the
fact
that
it is experimentally possible,
although
with a bigger inaccuracy,
to
determine
the
quantity
8
by
means
of
the
following
considerations.
r2
+8
2
,2
+ (R -
8)2
=
R2
R =
--
o 0 0
28
The
height
of
throw
Zo
is
computed
from
this as follows:
1
4cr8
Zo
=
-(Pi
- Po) + 2
2'
pg
PFg(r
+8
)
Po
L------"'
/.------,
1-------------,
c..-=-=-=-
z~-=-J
!-
-_=_-
=_-
=_-=_-
=_-
=
-_=
- - - - - - - 1
_ _ _ _ _ _ _
=-------
---=-J
1_______
-
--
0
__
1
~==============
=
-=-=-=-=
=-===~
~~=-==-=-~-=-~-=-~-=-~-=~=-=-::=-=~=-j
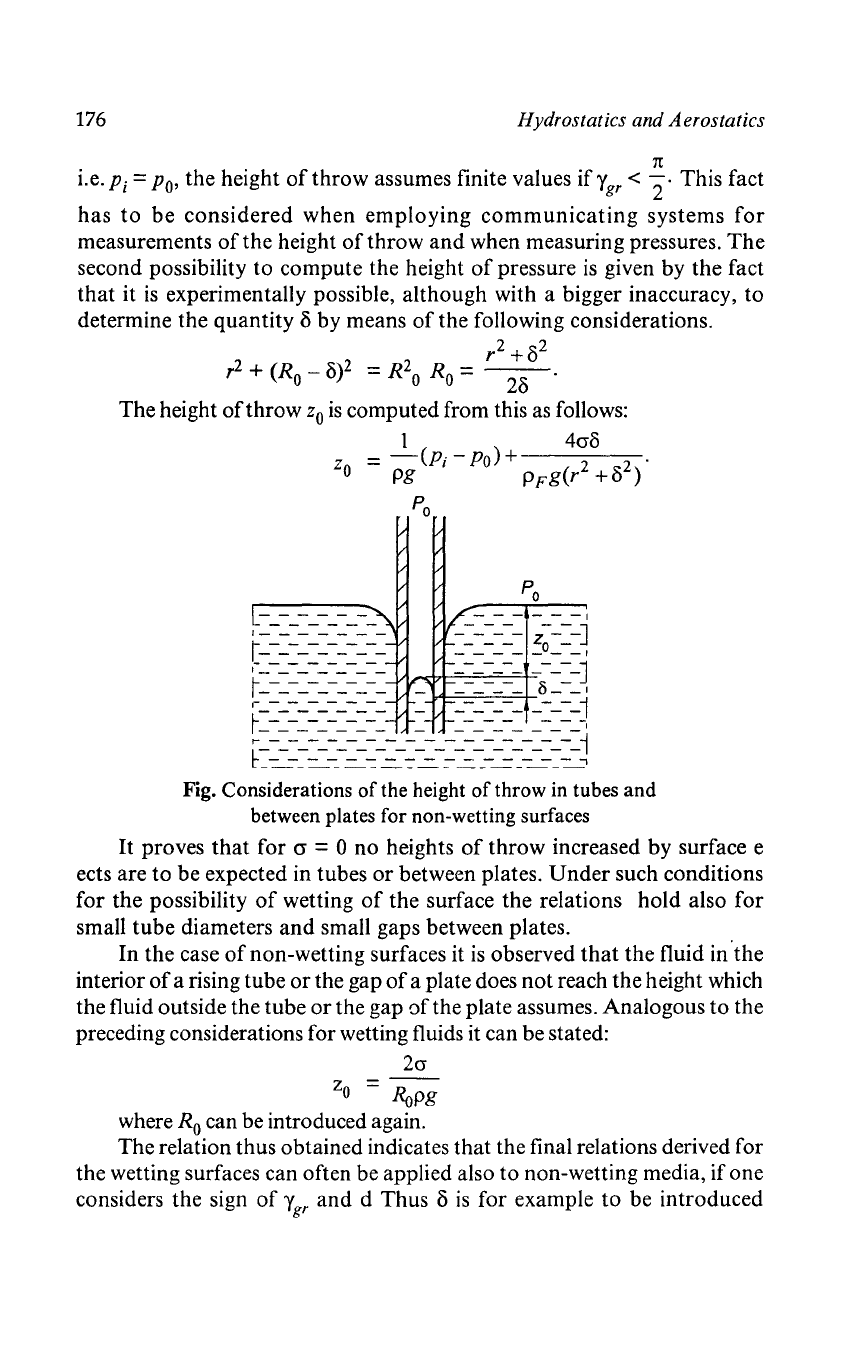
Fig. Considerations
of
the height
of
throw in tubes
and
between plates for non-wetting surfaces
It
proves
that
for
cr
= 0
no
heights
of
throw
increased
by
surface e
ects
are
to
be
expected in
tubes
or
between
plates.
Under
such
conditions
for
the
possibility
of
wetting
of
the
surface
the
relations
hold
also
for
small
tube
diameters
and
small gaps
between
plates.
In
the
case
of
non-wetting
surfaces it is
observed
that
the
fluid
in'the
interior
of
a rising
tube
or
the
gap
of
a
plate
does
not
reach
the
height which
the
fluid
outside
the
tube
or
the
gap
of
the
plate
assumes.
Analogous
to
the
preceding considerations
for
wetting fluids it can
be
stated:
2cr
z
=--
o Ropg
where
Ro
can be introduced again.
The
relation
thus
obtained
indicates
that
the
final relations derived
for
the
wetting surfaces can
often
be
applied also
to
non-wetting
media,
if
one
considers
the
sign
of
Ygr
and
d
Thus
8
is
for
example
to
be
introduced
Hydrostatics and Aerostatics
177
positively for wetting fluids in the above relations, whereas for non-wetting
surfaces d has
to
be
inserted negatively.
Bubble Formation at Nozzles
The
injection
of
gases
into
fluids
for
chemical reactions
or
for
an
exchangeof-materials represents a process which
is
employed in many fields
of
process engineering. Thus bubble formation
on
nozzles as
an
introducing
process
is
of
interest for these applications. Moreover, the simulation
of
boiling
processes, where the steam bubbles are replaced by gas bubbles, represents
another field, where precise knowledge
of
bubble formation
is
required.
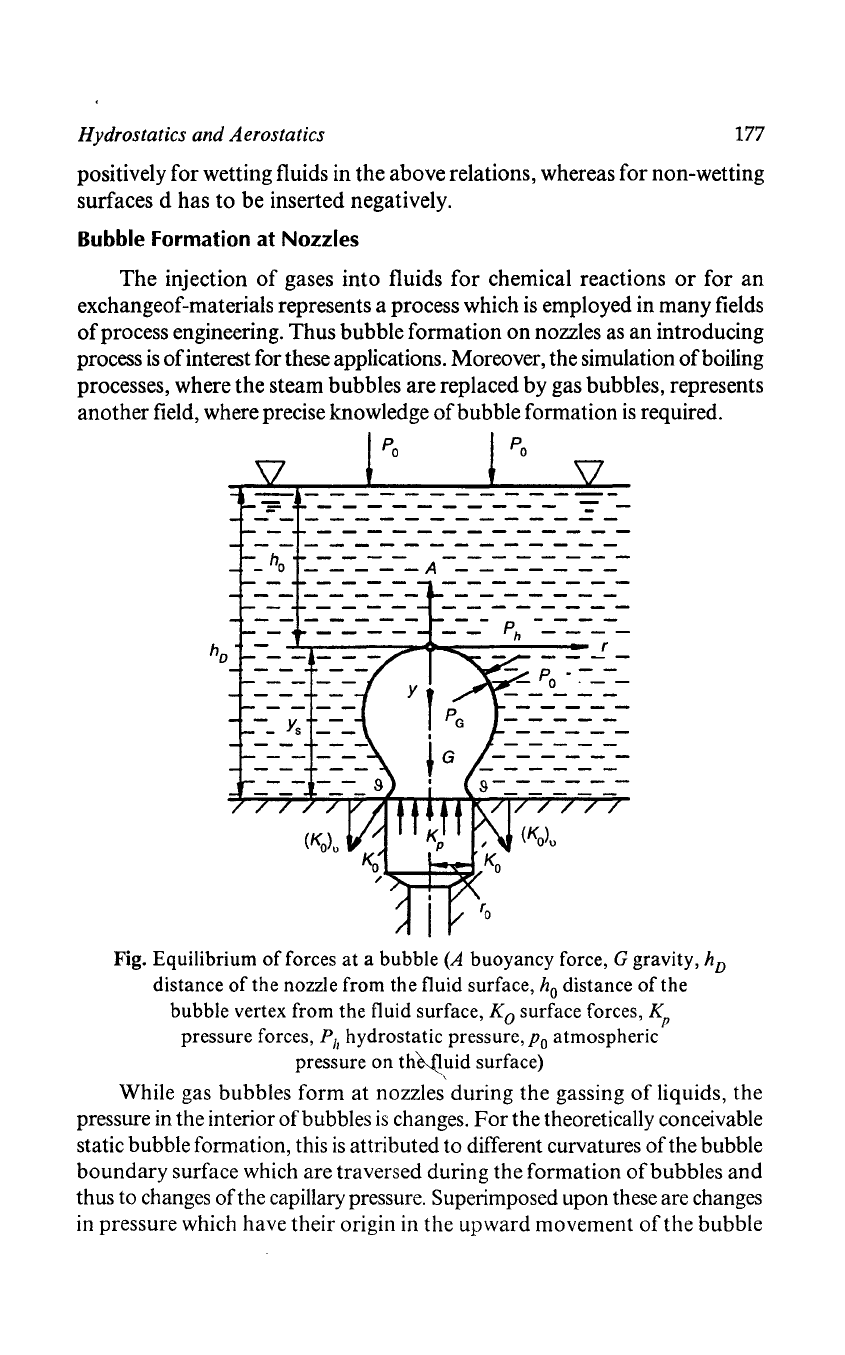
Po
_
ho
_-_-_-_-_
A
-_-_-_-_-_-_-_-
----
Ph
--------
r
Fig. Equilibrium
of
forces
at
a bubble
(A
buoyancy force, G gravity,
hD
distance
of
the nozzle from the fluid surface,
ho
distance
of
the
bubble vertex from the fluid surface,
Ko
surface forces,
Kp
pressure forces,
Ph
hydrostatic pressure,
Po
atmospheric
pressure on
th~~id
surface)
While gas bubbles form at nozzles during the gassing
of
liquids, the
pressure in the interior
of
bubbles
is
changes.
For
the theoretically conceivable
static bubble formation, this
is
attributed to different curvatures
of
the bubble
boundary
surface which are traversed during the formation
of
bubbles
and
thus to changes
of
the capillary pressure. Superimposed upon these are changes
in pressure which have their origin in the upward movement
of
the
bubble

178
Hydrostatics and Aerostatics
vertex
taking
place during the formation. With the dynamic formation
of
bubbles additional changing pressure e ects are
to
be
expected which
are
essentially based
on
accelerative
and
frictional forces.'
By
static bubble formation one understands the formation
of
bubbles under
pressure conditions, which allow
to
neglect the pressure effects
on
an element
of
the interface
boundary
surface due
to
accelerative
and
frictional forces.
Although in practice this
is
the case only
to
a very limited extent,
the
static
bubble formation has a certain importance.
As
it
is
theoretically conceivable, some important basic knowledge can
be gained from it
whi'ih contributes
to
the general understanding
of
bubble
formation.
Furthermore,
knowledge
is
required
on
the static bubble formation
in order
to
investigate the influences
of
the accelerative
and
frictional forces
in the case
of
dynamic formation
of
the
bubbles.
The
essential basic equations
of
static bubble formation can be derived
from the equilibrium conditions for the pressure forces
at
a boundary-surface
element.
For
the
pressure equilibrium
at
an
element
of
the interface
boundary
surface holds, that the gas pressure in the bubble
PG
has to be equal
to
the sum
of
the hydrostatic pressure
Ph
and
the capillary pressure P
cr
PG=Pcr+Ph =
(~1
+
;2)cr+PO+PFg(ho+Y).
Here the gas pressure
is
PG
=
PG,O
+ P($Y
When
one
considers the definition for the radii
of
curvature, with a as
Laplace constant
and
R
j
= R j / a, r = r / a y = Y / a the following differential
equation can be derived:
Y + Y
=2
__
Y
-w
-,
(1)
(l +
).1'2)3/2
r(1
+ y,2)1/2
Ro
.
By
the substitution
of
-,
- Y .
fI
Z =
=Slncr
~1+
y,2
the differential equation
of
second order can be replaced by a system
of
two differential equations
of
first order
-
rz)=
r
-=--y
,
d
(--
2-(
1
-)
~
Ro

Hydrostatics and Aerostatics
179
ciy
z
-=
~=tanS,
ar
"'1-
z2
which are used for integration.
The
desired bubble volume V
is
obtained in dimensionless form by the following partial integration
y y
V =
1t
fr2ciy
=
1tr2y
-
21t
fryar
o 0
and with the use
of
equation
V
=1tr[z
+r(y -
R~o)l
If
one introduces again dimension-possessing quantities, the equation
can be written
as
follows:
~
~~(~)[z
+~(~
-
~)l
V
~a3nr[
Z +
:'
(Y-
~Jl
With a
and
equation the bubble volume V can be written as:
V=
2cr
1tr{sins+~g(pF
-po)[Y-
2cr
]}.
g(PF
-Po)
2cr
g(PF
-Po)Ro
Equation represents an integral form
of
the differential equation
system which allows considerations
on
the equilibrium
of
forces
on
bubbles.
For
the forces acting on a bubble, the equilibrium condition can
be written in the form
VgPF
- Vgpo +
1tr2
[~
- g(PF -
Po)y
] = 21tr<JsinS
where the first two terms represent the buoyancy force and the weight
of
the bubble and the third term on the left side
is
the pressure force on
the bubble crosssection
1tr2 and the height y The surface forces are indicated
on the
right side. Equation should be employed in such cases where the
bubble volume
is
to be computed from the conditions
of
the equilibrium
of
forces.
For
the computation
of
the pressure changes the pressure in the
bubble vertex, owing to a transformation
of
the equations, can be expressed
as
stated below:
2cr
Po,o
=
Ro
+
Po
+
PFg(h
D
-
Y
s
);
For
the pressure at the nozzle mouth varies according to equations

180
Hydrostatics
and
Aerostatics
2cr
PG,D
=
Ro
+
Po
+
{JFgh
D
-
g({JF
-
{Jg)Ys;
Equation can be written in dimensionless form:
- 1 [
h]
1_
iY.PD
=
'2
( )
PG,D
- Po -
{JFg
D =
p_
- ys-
"
gcr
{JF
-
{JG
A'Q
Although the differential-equation system permits the com-putation
of
all bubble forms
of
the static bubble formation
and
by means
of
equations, the corresponding bubble volumes and pres-sure differences
can be obtained as important quantities
of
the bubbles, the problem with
regard to the single steps
of
the bubble formation
is
indefinite/uncertain.
The solution
of
the equations only allows the computation
of
a one-
parameter set
of
curves, where the vertex radius
Ro
is
introduced into the
derivations as a parameter.
It does not permit to predict in which order
the
different values
of
the
parameter
are traversed. This has
to
be
introduced into the considerations as an additional information in order
to obtain a set
of
bubble forms that are traversed in the course
of
the
bubble formation. Theoretically it
is
now possible to choose any finite,
ordered quantity
of
Ro
i values and to compute for these the corresponding
bubble forms.
Ofpract'ical importance, however,
is
only one
Ro
i variation,
which
is
given by most
of
the experimental conditions and' for which
conditions have been formulated
as
follows:
• All bubbles form above a nozzle with the radius
rD
.
,..
-
•
Ro,i
=
00.
As starting point
of
the static bubble formation the
horizontal position
of
the interface boundary surface above the
nozzle
is
chosen.
All further vertex radii are selected according to the condition
V
D
[Ro,l+l]
~
V
D
[Ro,l
]
This means that the theoretical investigations are restricted to the
bubble formation which comes about through a slow
and
continuous gas
feeding through nozzles having a radius
of
rD
. Gas refluxes through the
nozzles, and thus a decrease
of
the bubble volume with mounting vertex
radius,
as
equations would make possible, are excfuded by relation
c)
from
the considerations. The consequent application
of
this relation leads to
the formation
of
a maximum bubble volume. Same has to be considered
as
volume
of
the bubble at the start
of
the separation process, i.e.
- -
VA
=
(VD)max'
In the computations the differential equation system was solved
numerically for different vertex radii, considering the indicated conditions,
Hydrostatics and Aerostatics 181
and
thus the bubble form was ascertained. They can be consulted for the
comprehension
of
the static bubble formation
on
nozzles in fluids.
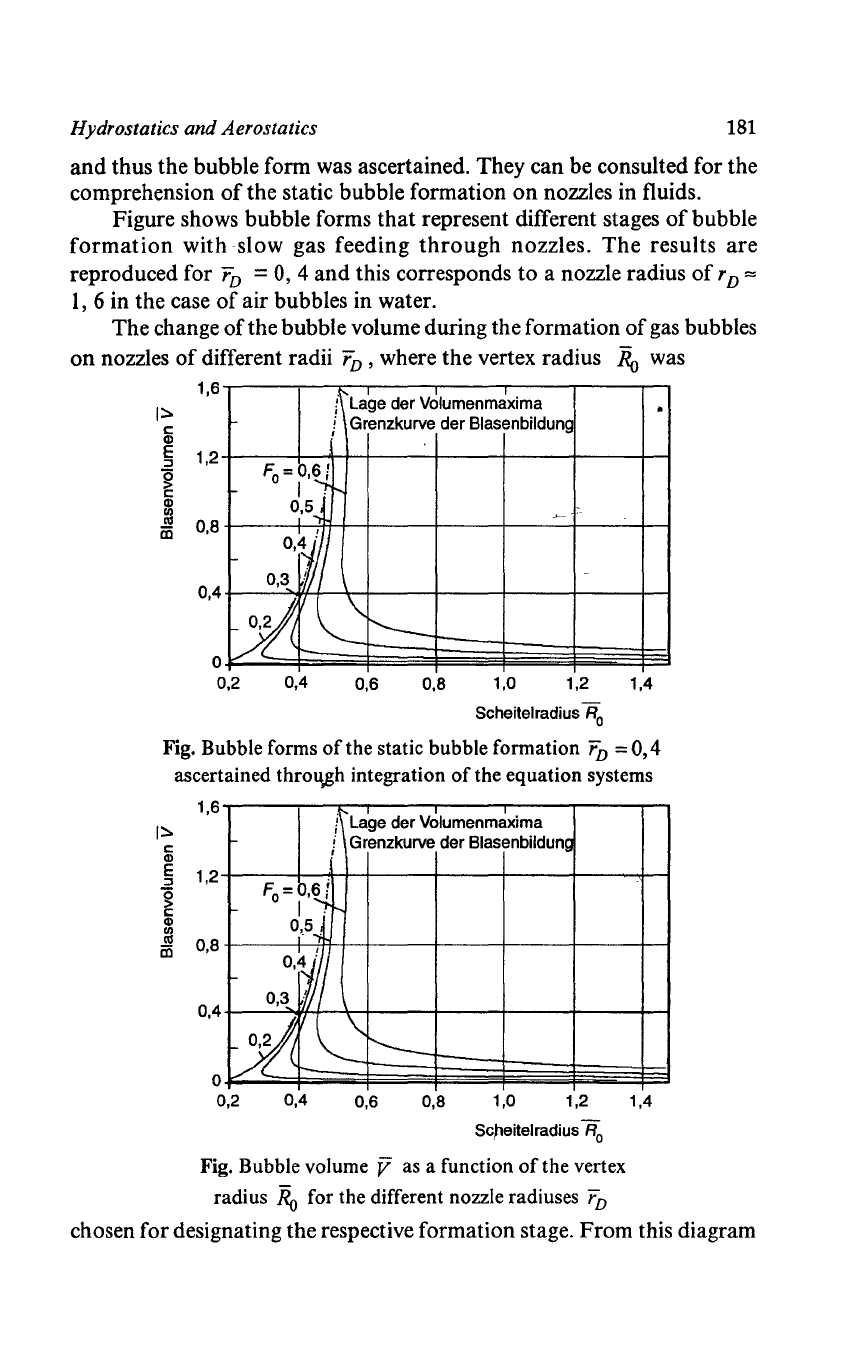
Figure shows bubble forms that represent different stages
of
bubble
formation
with slow gas feeding
through
nozzles.
The
results are
reproduced for
rD
=
0,
4
and
this corresponds to a nozzle radius
of
r
D
::=
I, 6 in the case
of
air bubbles in water.
The change
of
the bubble volume during the formation
of
gas bubbles
on
nozzles
of
different radii
rD
' where the vertex radius
Ro
was
1::'-
C
Ql
1,6~----.--.~~
•
.---~-----.-----r-----r1
i\
Lage der Volumenmaxima •
f Grenzkurve der Blasenbildung
§
1,24----f-+++-----jr----+---t---+-I
"0
Fo=O,~
£:
I
!"t--
~f-_
.-
~
0,5-.;
M
0,8+-----~,~~~--~-----+----~----~~
...
O'N)
0,3
Wi
0,2
0,4
0,6 0,8
1,0 1,2 1,4
Scheitelradius
Ro
Fig. Bubble forms
of
the static bubble formation
rD
=
0,4
1::'-
c
Ql
E
:l
~
Ql
~
10
ascertained
thro~h
integration
of
the equation systems
1,6
-r------r---.;'\':--,,.------,----.....,.------.-----r--,
II
Lage der Volumenmaxima
f Grenzkurve der Blasenbildung
1,2
0,8
0,4
O,~
0,3
W,
0,2
0,4
0,6 0,8
1,0
1,2
Screitelradius
Ro
Fig. Bubble volume V as a function
of
the vertex
radius
Ro
for the different nozzle radiuses
rD
1,4
chosen for designating the respective formation stage. From this diagram
