Brewster H.D. Fluid Mechanics
Подождите немного. Документ загружается.


92 Basics
of
Fluid Kinematics
+
{~(aU3
_
aU
2
)8x
2
+
~(aU3
_
au!
)8X!}
2
aX2
aX3
2
ax!
aX3
The
expressions
in
front
of
the
rectangular
brackets
represent
the
translation
which
is given
by
the following
velocity
vector:
~(Xl'
t) =
{U!'
U
2
' U
3
}
In
the
square brackets the
product
of
the
deformation
tensor:
au]
ax!
~(aU2
+ aul.)
2
ax!
aX2
~(aU3
+ au])
2
ax!
aX3
and
of
the
'"
distance
vector'"
{8xJ =
{8x!,
oX
2
'
OX
3
}
is
shown,
while in
the
curved brackets
the
vector
product
of
{8xJ =
{8x!,
oX
2
'
8x
3
}
and
is shown.
Thus
it can
be
written:
~(x
+ dx
i
, t) =
~(xi'
t) + D/xi' t)
oX
i
+ cijkwk
(Xi'
t)
oX
i
This
relation
again expresses
the
facts ofthe-
case
that
the
total motion
of
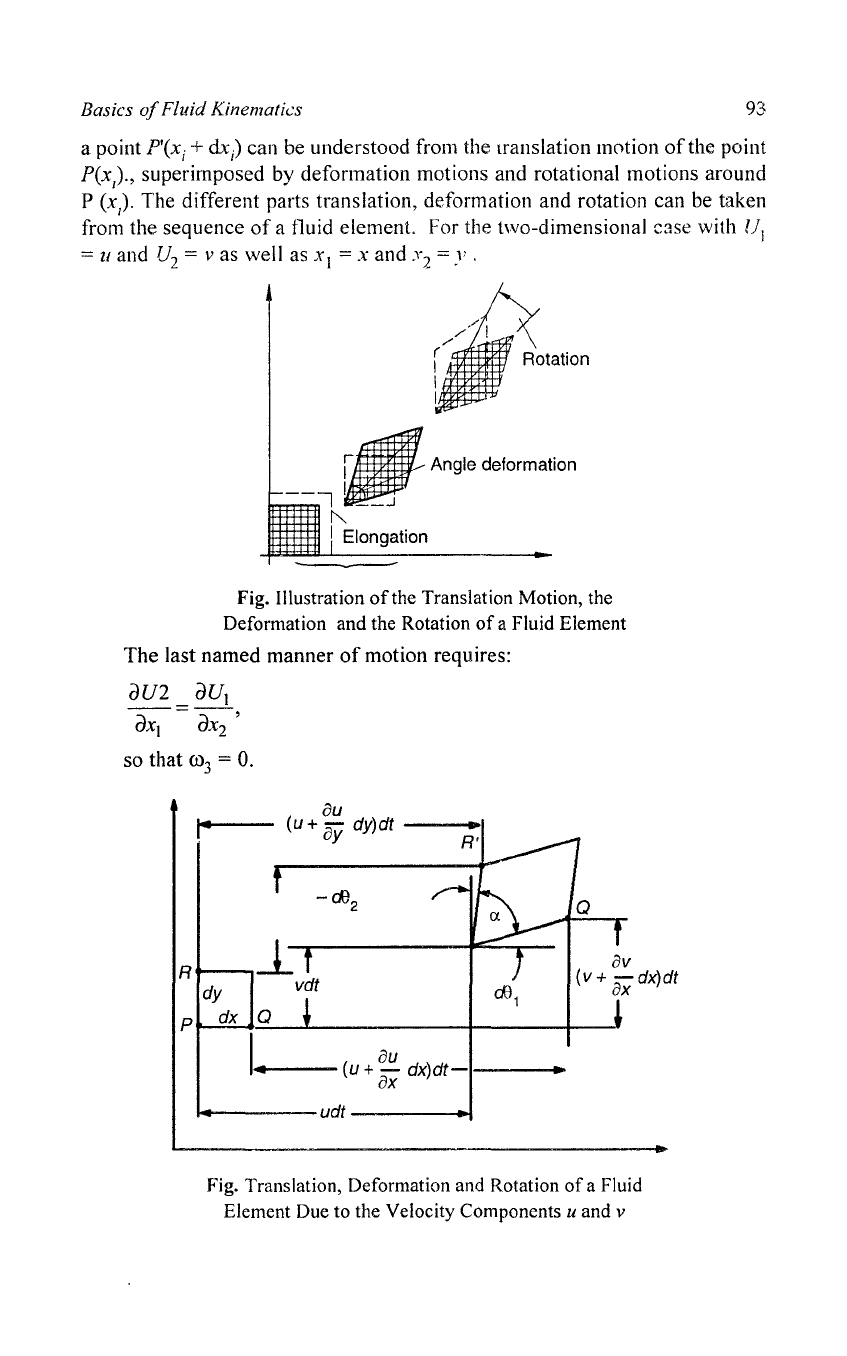
Basics
of
Fluid Kinematics
93
a point P'(x
j
+
ill)
can be understood from the lranslation motion
of
the point
P(xJ,
superimposed by deformation motions and rotational motions around
P (x). The different parts translation, deformation and rotation can be taken
from the sequence
of
a fluid element. For the two-dimensional case with
lJ
l
= u and U
2
=
vas
well as
xI
= x
and.l
2
= y .
II
I Angle deformation
__
, I
• I
__
..1
'"
I Elongation
Fig. Illustration
of
the Translation Motion, the
Deformation and the Rotation
of
a Fluid Element
The last named manner
of
motion requires:
aU2
au!
ax!
aX2
'
so that
00
3
=
o.
au
(u+
ay dy)dt
---1;"',1
av
(v+
ax dx)dt
~~~~-------+----~~
Fig. Translation, Deformation and Rotation
of
a Fluid
Element Due to the Velocity Components
u and v
94 Basics
of
Fluid Kinematics
y
p
~--------------------
..
x
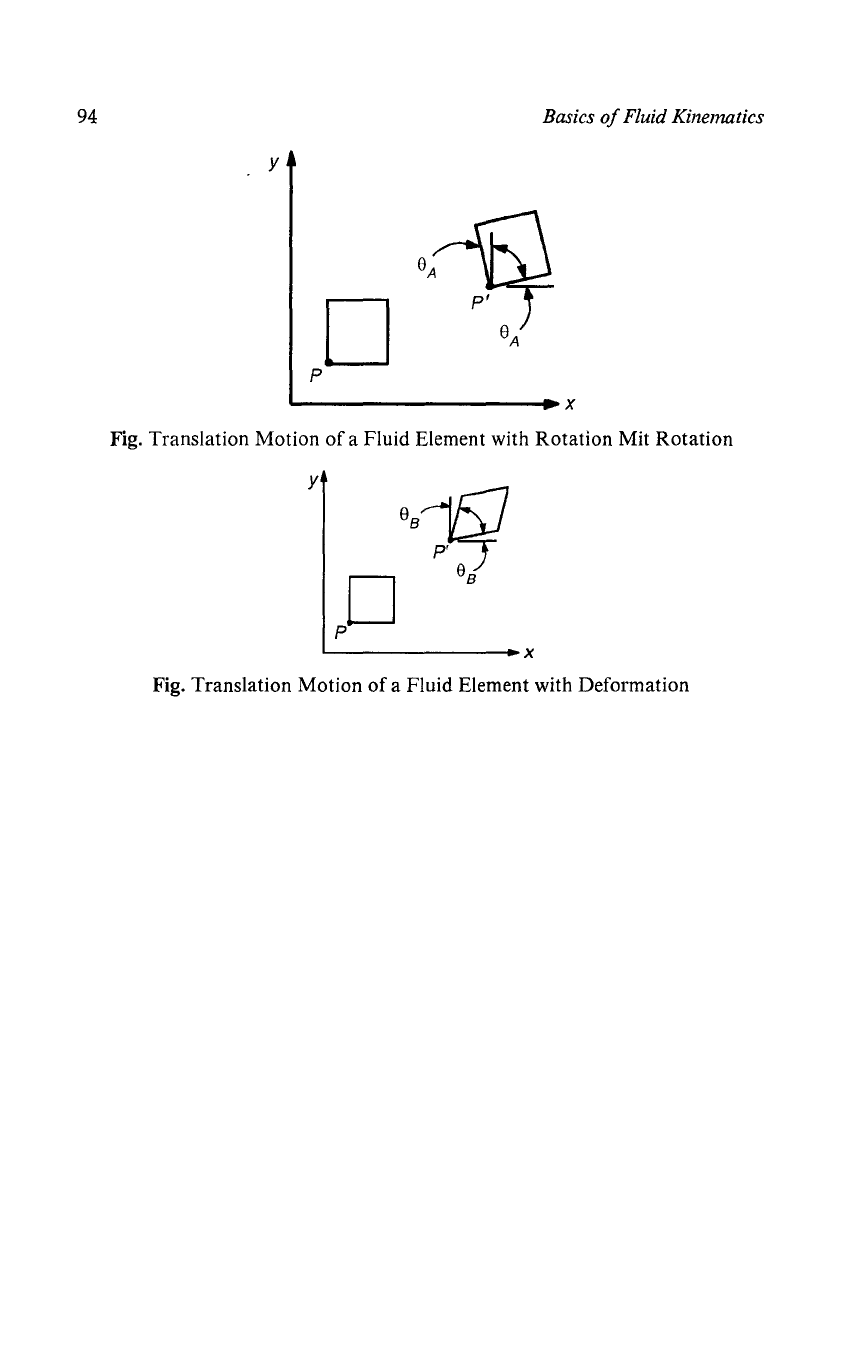
Fig.
Translation Motion
of
a Fluid Element with
Rotation
Mit
Rotation
y
L--------
..
x
Fig. Translation
Motion
of
a Fluid Element with Deformation

Chapter 4
Basic
Equations
of
Fluid
Mechanics
GENERAL CONSIDERATIONS
Fluid mechanics considerations are carried
out
in many domains,
especially in the fields
of
engineering. Below there
is
a list which clearly
indicates the far-reaching application
of
fluid-mechanics knowledge. The list
lends itself to show the importance
of
fluid mechanics. While it was usual in
the
past
to
carry out special fluid-mechanics considerations
on
each
of
the below-listed domains, today one strives increasingly at developing
and
introducing
generalized
ways
of
consideration
that
are
applicable
unreservedly
to
all below-cited domains. This makes it necessary
to
derive
the basic laws formulated for the application
of
solving flow problems so
generally
that
they fulfill the requirements
for
broadest
applicability
indicated in the below-cited list.
The
objective
of
the derivations in this
section
is
to
formulate the conservation laws for mass, momentum, energy,
chemical species etc. such
that
they can be applied to all the flow problems
occurring in the following domains:
•
Heat
exchanger, cooling
and
drying technology
• Reaction technology and reactor layout
• Aerodynamics
of
vehicles and aero planes
• Semiconductor-crystal production, thin-film technology, vapour-
phase separation processes
• Layout
and
optimization
of
pumps, valves
and
nozzles
• Usage
of
flow aggregates like bent pipes, junctions
etc.
• Development
of
measuring instruments and production
of
sensors
• Ventilation, heating
and
air-conditioning techniques, function
of
labora-tory vents
• Problem solutions
in
roof ventilation and flows around buildings
•
Production
of
electronic components, micro-systems analysis
engineering
• Layout
of
stirrer systems, propellers and turbines
• Sub-domains
of
biomedicine
and
medical engineering
• Layout
of
baking ovens, melting furnaces
as
well
as
other fire places

96
Basic Equations
of
Fluid Mechanics
• Development
of
engines, catalyzers and exhaust systems
•
Combustion
and
explosion
processes,
energy
generation,
environmental
engineering
Sprays, atomizing and coating technologies
Concerning the formulation
of
the basic equations
of
fluid mechanics it
is
easy to formulate the conservation equations for mass, momentum, energy
and chemical species for a fluid element, i.e. to derive
in
the "Lagrange form"
of
the equations.
In
this way the derivations can be represented
in
an easily
comprehensible way and it
is
possible to build the derivations upon the basic
knowledge
of
physics. Derivations
of
the basic equations
in
the Lagrange form
are usually followed by transformation considerations whose aim
is
to strive
at local formulations
of
the conservation equations and to introduce field
quantities into the mathematical representations, i.e. the
"Euler form"
of
the
conservation equations
is
sought for solutions
of
flow-mechanical problems.
This requires to express temporal modifications
of
substantial quantities as
temporal modifications
of
field quantities or to complement them in a
deepening way.
M = Gesamtmasse
des betrachteten
Fluids
M = L!jldmg; = const
Fig. Division
of
a fluid in fluid elements
The considerations to be carried out apart from the assumption that at a
certain point in time
t = 0 the mass
of
a fluid
is
subdivided
in
fluid elements
of
the mass
om9\
i.e.
M=
Lom9\
9\
Here for each fluid element
om9\
is
to
be
chosen large enough to make
the assumption
om9\
= const possible with sufficient precision in spite
of
the
molecular structure
of
the matter, it also allows to assign a arbitrary thermo-
dynamical and fluid-mechanics properties
<X9\(x9\(t),
f) =
<X9\(t)
for a fluid
element and with a satisfactory precision for fluid-mechanics considerations.
The
statement
<X9\(x9\,
t),
with
x9\
=
x9\
(t),
expresses
that
the
thermodynamical or fluid-mechanics property, which is assigned to the
considered fluid element and thus only represents a substantial quantity,
is
only a func-tion
of
time. This property
of
the element
is
changing with time,

Basic Equations
of
Fluid Mechanics
97
also due to the motion
of
the fluid element and for the description
of
this
modification it
is
important that one follows the mass om9\' i.e. knows x9\(t)
and also takes it into consideration as known.
It
is
assumed that this motion
of
particles
is
constant and unequivocal, i.e. that the considered fluid element
does not split up during the considerations
of
its motion. The fluid pertaining
to the considered fluid element at the moment
in
time t = 0 remains also at all
later moments
in
time. This signifies that it
is
not possible for two different
fluid elements to take the same point in space at an arbitrary time:
x9\(t) =
xL(t) for
9\
*-
L.
When a fluid element
9\
is at the position xi' at the time t i.e. xi = (x9\(t»i
at the time
t,
then the substantial thermodynamic property or fluid property
u9\(t)
is
equal to the field quantity u at the point x; at time
t:
~(t)
= U(xi' t) when (x9\(t»i = xi at t
For the temporal change
of
a quantity u9\ (t) results:
dU9\
au au
(dx;
)
Tt=-at+
ax;
dt
9\
With (dx/dt)9\ = (U)9\ =
U;
holds:
dU9\
=
Da
=
au
+u
au
dt
Dt
at
I ax;
The operator
u(Xj'
t) applied to the field quantity
D/Dt
= u,iJ/ax
j
is often
defined
as
the substantial derivatve and will be applied in the subse-
quent derivations. Significance
of
individual terms are:
a/at = (a/at)x; = change with time at a fixed location,
partial differentiation with respect to time
d/dt= total change with time (for a fluid element),
total differentiation with respect to time
for e.g. for a fluid when
~
=
P9\
= const i.e. the density
is
constant, then
it holds:
dp9\
= Dp
=0
or
ap
=-U,.~
dt
Dt
at
ax;
When at a certain point in space a/at (u)xj = 0 indicate
of
stationary condi-
tions, i.e. the field size
u(x
j
,
t)
is
stationary and thus has no time dependency.
On the other hand
d(~)/dt
=
Du/Dt
=
0,
is
u9\ (t) =
u(Xj
, t) = const. i.e the
field
is
independent
of
space and time.
MASS
CONSERVATION
(CONTINUITY
EQUATION)
For fluid-mechanics considerations a "closed fluid system" can always
be found, i.e. a system for whose total mass holds
M = const. This
is
easily
seen for a fluid mass, which
is
stored
in
a container. For fluid setups, control
volumes can always
be
defined, within which the systemic total mass can be

98
Basic Equations
of
Fluid Mechanics
stated as constant.
If
necessary these control volumes can comprise the whole
earth.
When one subdivides the fluid mass within the considered system in fluid
elements with the sub-masses dm, then it holds true for the temporal change
of
the total mass:
dM
d d
0=
- = - L (om9t) = L
-(om9t)
dt dt9t
9t
9t dt
Aquarium with , ,
constant
A~r-blast
~ystem/ventllator
quantity
of
water with suction and outler
,-------------,
1 ::::1
1
~I
~.~~~
1
mel'nl
~
-:;--:;-
-:;-......:
I I
f-
-:;-
-:;-
-:;-
-.: I I
~
-----
;--
-----
~~
___
'
~
____
J
r·
m.
-1-
M = const em M = const
Flow around a wing
~----
~
~
M=
canst
Fig. Different Fluid setups and aero foil within
control volumes where
M = const
This equation expresses that the mass conservation in the total fluid system
is
preserved when each individual fluid element conserves its mass
om9t.
With
this the balance equation for the mass conservation can be stated as
foUqws in
Lagrange notation: '
d(om9t) = 0
dt
The basic molecular structure
of
matter and thermal motion connected
with it indicates that to fulfil the above relation absolutely, it is necessary that
om9t
-7
0 The consideration carried out in this book therefore requires that all
the
om9t
are considered as finite but nevertheless as very small. A fluid element
with position coordinates
(x;)9t
is shown.
The estimation
of
Om9t
is referred to considerations, where it
is
shown
what dimensions a volume
of
an ideal gas has to have in order to define
"sufficiently clearly" e.g. a density
of
the gas within the volume, The
considerations carried out there would have to be repeated here
in
order to
guarantee
om9t
= const, in spite
of
the molecular structure
of
the matter. With
the choice
of
om9t
const the conditions are set to carry out continuum-mechanics
considerations for the motion
of
fluids, although the fluids show a molecular
structure. In this context it is often referred to the continuum considerations
in which usually fluid-mechanics considerations are carried out. Strictly
speaking this means that the properties
of
the molecules, especially their
transport properties, can only be introduced in fluid-mechanics considerations
in integral form.

Basic Equations
of
Fluid Mechanics
x
2
Xa
~=~nm
,(x
2
)9t
Fig. dm B =
Const,
Condition
for
the
Mass
of
a Fluid
Element
99
Because
of
the above explanations the mass conservation can be stated
as follows:
dM
=0
and
dO~
=0
dt dt
The above considerations confirm that it is very simple to formulate the
mass-conservation law in Lagrange variables. Working practically with the
law
of
mass conservation, however, requires its representation in field
quantities, i.e. the Lagrange form
of
mass-conservation law has to be brought
into the Euler form.
Transformed into Euler variables (i.e. into field quantities) one obtains
from equation for the mass conservation:
o =
~
=
(Om
) =
~(
OVc) =
d(OIV
9t
) +
OVc
d(P9t).
dt
9t
dt
P9t
9t
P9t
dt
9t
dt
'-------v-----'
'---v----'
I 1/
For term I in equation using
P9t
= P and
(x9t
(t»j =
Xj
at the time
t:
yields:
d(OIV
9t
)
OVc
au;
P9t
dt = P
9t
ax
..
I
For term II one obtains:
OVc
d(p9t) =
OVc
(a
p
+u.~).
9t
dt
9t
at
I
ax.
I
With the above derivations the substantial derivation
of
the corresponding
field quantity
d(p9t) Idt could be applied for p, d.
h.
DplDt
in order to achieve
the transition from the substantial quantity
P9t(t)
to the field quantity p(x
i
,
t).
The same procedure is not possible with
d(O
V
9t)
Idt since there are no volume
fields. From section 4, equation, concerning the temporal change
of
a fluid
element is equal to the divergence
of
the velocity field is known, however:
d(OV9t)
_
OVc
au;
P9t
dt
-
9t
ax
..
I

100
Basic Equations
of
Fluid Mechanics
When one inserts the equations one obtains:
oV9\
-+p-+U
j
-
=0,
[
a
p
au,
a
p
]
at
ax; ax;
As
oV9\
= 0 it follows for the continuity equation in the most general
form:
dP
+p
au,
+U.~=
ap
+
a(puJ
0
at ax· ' ax· at ax·
, , I
The equation can, also be written as follows:
ap ap
au;
Dp
au,
-+U,-+p--=-+p-
=0.
at
ax;
ax;
Dt
ax;
This form
of
the continuity equation is not very useful for the solution
of
flow problems. However it is very well suited for presentation
of
the basic
equations
of
fluid-mechanics in different ways, in order to bring out special
physical facts. As an example the special form
of
the
continuirj
equation for
P9t
= const, i.e. DplDt = 0, from equation:
aU
j
ax. = 0,
,
i.e. the divergence
of
the velocity field is zero for fields
of
constant density.
since the divergence
of
the velocity field is zero, the change in volume is also
zero from equation, this can also be obtained from the equations.
1 Dp 1
(a
p
)
DT
1
(a
p
)
DP
aU
j
p Dt = P
aT
p
Dt
+ P
ap
T Dt = -
ax;
'---v-----'
'---v----'
-p +a.
This relation expresses for a fluid in the thermodynamic sense, p = const,
i.e
if
the fluid density is constant, then it has to be thermodynamically incom-
pressible.
~
Dp = _
aU
j
= ° = a DP _ A
DT.
_ .
P Dt
ax;
Dt
t-'
Dt
wIth a - 0 where a and
~
are.
a = -
~
(~;)T
=
~(-~~)T
= isothermal compressibility coefficient
~
=
~
(~;
) p
=}(
~~
) p = thermal expansion coefficient
Thus the continuity equation holds in one
of
the two forms listed below:
ap a(pU
j
)
at+
ax;
= 0 (compressible flows)
(icompressible flows)

Basic Equations
of
Fluid Mechanics
101
SECOND
NEWTONIAN
LAW
(MOMENTUM
EQUATION)
The derivations
of
the equations
of
momentum for the three coordinate
di-rectionsj
=
1,2,3
in
fluid mechanics, the second Newtonian law to a fluid
element, i.e. the Lagrange formulation
of
the equation
of
momentum is cho-
sen. For a fluid element
it
is stated that the time derivative
of
the momentum
in the j-direction is equal to the sum
of
the external forces acting
in
this di-
rection on the fluid element, plus the molecular-dependent input per unit time.
The forces can be stated as inertia forces caused by gravitation forces
(8N~)
and electromagnetic forces
2
as well as the surface forces caused by pressure
(80.). After addition
of
a temporal change
of
momentum fed
in
by the molecular
mo~ement,
the equation
of
motion can be formulated as follows:
d(&Jjht =
L,(8M
j
)9t
+
L,(80
j
ht
+
(i.(&J
M
)j)
dt
'----v----'
'----v-----'
dt 9t
Inertia forces surface
forces'
v '
molecular-dependent
momentum input
Here, as stated in Figure, (~h = 8m(U)9t
Fig.
For
the
Derivation of
Momentum
Equations
The fluid element acts like a rigid body since it does not change its state
of
motion, i.e. its momentum, when no inertia
or
surfaces forces act on the
fluid element and a molecular-dependent momentum input fails to appear.
However, when forces are present,
or
when a momentum has input, the fluid
element changes its momentum in accordance with the above-stated relation.
It represents the Lagrange form
of
the equations
of
momentum
(j
= 1,2,3)
of
fluid mechanics.
In order to conserve the Euler form
of
the equation
of
momentum, it is
important to express each
of
the terms contained
in
equation
in
field quantities.
For the left side
of
the equation can be written as:
d(&J
j
ht
_
i.[8
(U)]
_ 8
d«U
j
ht)
(U)
d(8mht)
dt
-dt
m9t
j9t
- m9t dt +
j9t
dt
