Brewster H.D. Fluid Mechanics
Подождите немного. Документ загружается.

82
Basics
of
Fluid Kinematics
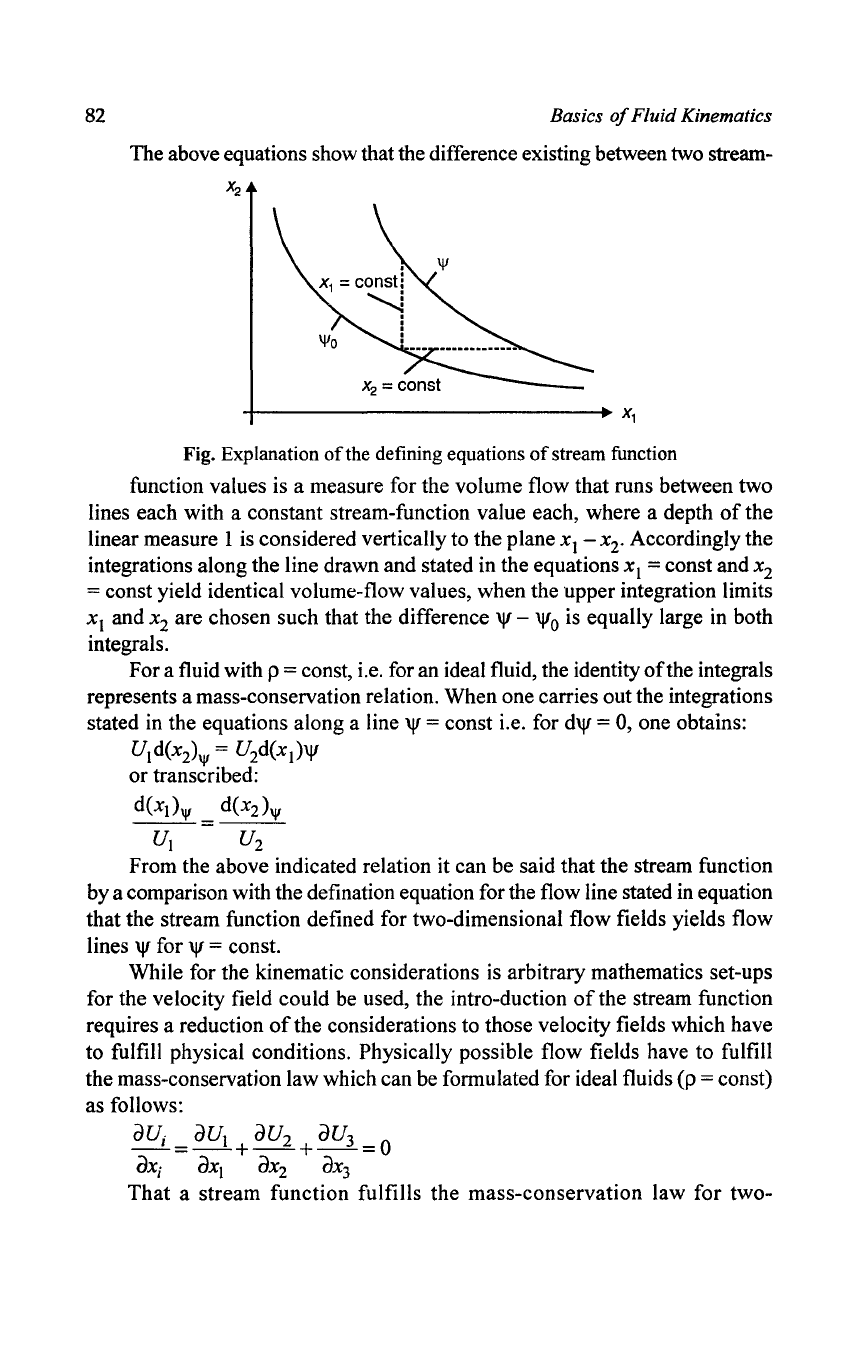
The above equations show that the difference existing between two strearn-
X
2
~----------------------------.~
Fig. Explanation
of
the defining equations
of
stream function
function values is a measure for the volume flow that runs between two
lines each with a constant stream-function value each, where a depth
ofthe
linear measure 1
is
considered vertically to the plane
xl
- x
2
• Accordingly the
integrations along the line drawn and stated in the equations
xl
= const and x
2
= const yield identical volume-flow values, when the upper integration limits
xl and x
2
are chosen such that the difference 'I' -
'1'0
is equally large in both
integrals.
For a fluid with
p = const, i.e. for an ideal fluid, the identity
of
the integrals
represents a mass-conservation relation. When one carries out the integrations
stated in the equations along a line
'I' = const i.e. for d'l' = 0, one obtains:
U
I
d(x
2
)1j1
= U
2
d(x
1)'1'
or transcribed:
d(xI)1j1
d(x2)1j1
---'-
=
---'-
U
I
U
2
From the above indicated relation it can be said that the stream function
by a comparison with the defination equation for the flow line stated
in
equation
that the stream function defined for two-dimensional flow fields yields flow
lines
'I' for 'I' = const.
While for the kinematic considerations is arbitrary mathematics set-ups
for the velocity field could be used, the intro-duction
of
the stream function
requires a reduction
of
the considerations to those velocity fields which have
to fulfill physical conditions. Physically possible flow fields have to fulfill
the mass-conservation law which can be formulated for ideal fluids (p
= const)
as follows:
au;
=
aU
I +
aU
2 +
aU
3
=0
ax;
aXI
aX2
aX3
That a stream function fulfills the mass-conservation law for two-

Basics
of
Fluid Kinematics 83
dimensional flows automatically, can easily be checked by inserting the
definition in equation where the law/principle
of
Schwarz has to be
applied-.
When a flow field does not fulfill the mass-conservation law, the
integrations to be carried out according to the equations result
in
solutions
contradicting one another. This can be shown for the employed two-
dimensional flow field which does not fulfill the mass-conservation law (i.e.
the continuity equation):
U
I
= xl; U
2
= x
2
(1
+ 2/) and U
3
= 0
When one carries out the integration stated
in
equation
in
spite
of
this,
from the defining equations for the stream function, i.e. from the relations
results:
a",
a",
-=xI
and
-=-x2(1+2t)
aX2
aXI
By integration
of
these equations one obtains for the stream function:
'V
=
xl
X
2
+ F(XI' t)
'V
=
-x
l
x
2
(1
+
2/)
+ G(X2' t)
or expressed otherwise:
x
l
x
2
+
F(xI'
t) *
-Xl
x
2
(1
+
2/)
+ G(X2' t)
or
2(t
+
l)xl
X
2
*
G(x
2
,
I)
-F(XI'
t)
A comparison
of
the results
of
both the integrations, which yield the
equations shows the contradiction resulting for the stream function.
The time dependence showing on the right side
of
the relation is missing
on the left side. This results from the fact that the velocity field indicated
according to although mathematically clearly defined, cannot exist
ph~ically;
the velocity field does not fulfill the requirements determined by the mass-
conservation law for p
= const When one considers on the other hand the
velocity field:
U
I
= exp [x
l
(1
+ t)]; U
2
=
-x
2
(1
+
t)
exp [xl
(1
+ t)]; U
3
= 0 for which
the relation is fulfilled, where it holds:
aU
I
aXI
=
(1
+ t) exp
[x
I
(1
+
t)]
and
aU
2
aX2
=
-(1
+ t) exp [xI(1 +
I)]
one obtains from the defining equations for the stream function :
a'll
aX2
= exp
[x
l
(1
+
I)]
and
a'll
aXI
= x
2
(1
+t) exp
[x
l
(1
+
I)]

84
Basics
of
Fluid Kinematics
the following solution for the stream function
'1':
'I' = X
2
exp
[x
l
(1
+
t)]
+ C
If
one knows the value
of
the stream function for xl 0 and x
2
0 ' it holds
'1'0
= x
2
'
0 exp
[Xl'
0
(1
+ t)] + C "
'I' -
'1'0
= X
2
exp [xl(J +
t)]
- X
2
, 0 exp [XI,O
(l
+
t)]
The obtained result can also be computed for xl = x
LO
= const . from the
relation:
'I' -
'1'0
= (x
2
- x
2
0)
exp
[Xl
0(1
+
t)]
for
Xl
=
Xl
0
This is indicll.ted by the distribution 'I'(x
2
)
at the'location
Xl
0 an.
When one wants to determine the flow line path in the plane
Xl
- X
2
- one
has to consider
y as a parameter in equation and derive the relation x
2
-
Xl
-
for this parameter from equation. Here
'1'0'
x"O and x
2
'
0 are constants that
can be chosen freely.
Divergence
of
a Flow Field
In this section matherr:atics operators shall be explained that are known
from vector analysis and that can be applied to flow fields. Their derivations
will also be repeated and considered as concerns their physical meaning.
Diveigence
of
the stream field
u:
au;
au!
aU
2
aU
3
--=--+--+--
aXi
aXI
aX2
aX3
The above defined divergence
of
a flow field is to be considered as a
scalar
:Q~ld
which, in the presence
of
a steady velocity field, is defined at each
point in space and can be computed from the velocity field that can
be
assumed
to be known.
When one wants to perceive the physical meaning
of
the operator Vi
a
applied to the velocity field
ax.
Xi the consideration
of
a fluid element, as
I
stated in Fig.4.9, is recommended.
x
2
H
D~_+--_--..::'1'
Q :
}----------
-------r----
..
,,,;'
,"E
~A
~~
/x~
~Xl
3
au
Fig. Fluid element for explaining the physical meaning
of
~
ox;

Basics
of
Fluid Kinematics
85
The edge lengths
~i
were assumed
to
be very small, so that a velocity
vector can be assigned to each surface such that this vector indicates with
which velocity the considered surface
of
a fluid element moves. Accordingly,
the surface AEHD moves in the direction
XI
with the velocity component
of
the velocity field present in point Q i.e. with U
I
(x)
= U
I
(xI'
x
2
' x
3
).
In
comparison, the
<;urface
BFGC moves with the velocity component UI(x, +
Dx
"
x
2
' x
3
).present
in
point
P.
This velocity component can be expressed
by
a
Taylor series expansion as follows:
. _
(au
l
)
1(a
2
U!)
2
UI(X
I
+
Dx
l
, x
2
'
x
3
) -
UI(x!)+
-
~!
+-
-2-
~I
+
...
ax!
2
ax!
The
difference velocity between the surfaces
AEHD
and
BFGC
can
thus
be computed as:
(
au!)
1
(a
2
U
I
)
2
~U!(xi'~)
=
--~!
+-
-2-
~!
+
...
ax!
2
ax!
As a consequence
of
this velocity difference a volume increase
or
a volume
decrease results, depending on which signs the derivations
of
the velocity fields,
which can be stated as follows in a first approximation
by
multiplication with
the surface
~2
~3'
neglecting the terms
of
second and higher order in
~!:
d
s:
au!
-(uT1ht
=~U!(x')(~2~3)=-~!(~2~3)
dt
ax!
On
the basis
of
simultaneously existing gradients
of
the velocity field in
the directions
x
2
- and
x3
in addition volume changes
occur
in the time unit,
which again can be stated in a first approximation as follows:
~(OV2)9\
=
aU
2
~2(~!~3)
and
dt
aX2
d
aU
3
-(OV3h
=
-~3(Llx!~2)
dt
aX3
so that the entire volume change that
can
be expected in a flow field for
a fluid element in the time unit can be indicated as follows:
d 3 d
au,
-(OV3h,=
L-(OV
a
)9\
=:\(OV9\)
dt
a=!
dt
oXi
or can be written as:
au,
=
_l_~(OV9t)
aXi
OV9\
dt
This relation makes emphasizes the physical significance
of
the divergence

86
Basics
of
Fluid Kinematics
of
a vel(lcity field. In accordance the divergence
of
a velocity field states how
big the volume change
of
a fluid element is that occurs per time and volume
unit at a certain position
in
a flow field. At such locations
of
the flow field
where the divergence
of
a velocity vector
is
equal to zero, there is
no
temporal
volume change locally for a fluid element moving in the velocity field. When
the divergence in sub-domains
of
the velocity field is computed negatively, a
fluid element experiences volume decreases in these domains.
When one carries out considerations concerning the physical significance
ofthe
divergence
of
a velocity field at a stationary volume element
of
a fluid,
inflows and outflows occur through the surfaces
of
the considered volume
because
of
the existing velocity field, to an extent that the volume flowing in
per time unit can be
stated:
V
inflow
=
U;llX
j
l:1
xk
i =
j,
k
For the volume flowing out it can be computed:
. [au"]
VOutflow
= U
j
+
ax;'
llXjllXk i =
j,
k
The relation makes clear that the sumation for i = 1 to 3 is stated in a
sufficient6ly comprehensible way by the double index in
au;
/
ax;
The difference
of
inflows and outflows, considering DV = Dx
1
,
DX2
'
DX3
can be computed as:
..
."
au.
I:1V=V
Inflow
-VOutflow
=---'I:1V
ax;
This relation makes clear that the presence
of
a positive divergence
of
the velocity field in volume
is
equal to a source, as more "'fluid volume'" is
flow!ng out than flowing in. When, however, the divergence
of
a velocity field
is negative, a sink occurs, as then the inflow in
'"volume''' has to be larger
than the outflow.
TRANSLATION,
DEFORMATION
AND
ROTATION
OF
FLUID
ELEMENTS
Analogous to considerations in solid-state mechanics, the deformations
of
fluid elements that occur due to existing velocity gradients are
of
interest
in some flow-mechanics considerations.
When one includes the translatory motion and the rotation
of
a fluid
element in the fluid deformations, the entire local state
of
motion
and
deformation can
be
stated by
four'"
geometrically easily separable'" sub-states.
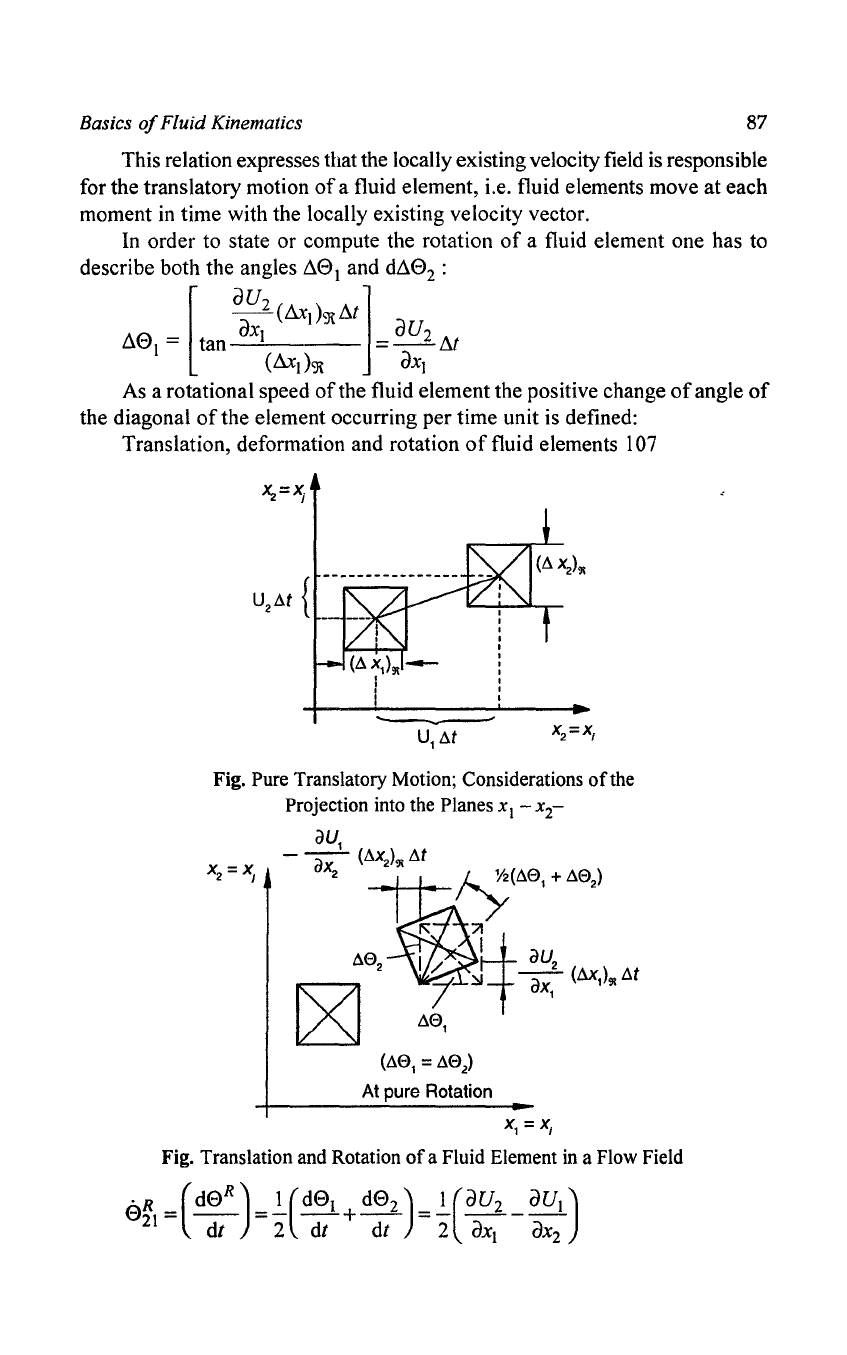
The pure translatory motion leads to a change
of
position
of
the fluid element
marked to an extent that it holds:
d(-).)
=
(~)9t
dt =
~dt
Basics
of
Fluid Kinematics
87
This relation expresses that the locally existing velocity field
is
responsible
for the translatory motion
of
a fluid element, i.e. fluid elements move
at
each
moment
in
time with the locally existing velocity vector.
In order to state or compute the rotation
of
a fluid element one has to
describe both the angles
~el
and
d~e2
:
[
aU2
1
-(,ixlh
M
a
~el
= tan aXI = U
2
M
(,ixlh
aXI
As a rotational speed
of
the fluid element the positive change
of
angle
of
the diagonal
of
the element occurring per time unit is defined:
Translation, deformation and rotation
of
fluid elements 107
Fig. Pure Translatory Motion; Considerations
of
the
Projection into the Planes x
I - x
2
-
aU
1
-
--ax-
(~~)\l!
M
x
2
=
~
2
:!ir;(M~1
+
~e2)
~e2
~
/
71~
aU
2
/
~t
ax,
(~l)91M
~
Ae,
(~el
=
~e2)
At
pure
Rotation
Fig. Translation and Rotation
of
a Fluid Element in a Flow Field
e~l
=(deR)=~(del
+
de2)=~(aU2
_
au
l
)
ili
2
ili
ili
2
~
~

88
Basics
of
Fluid Kinematics
Thus generally the components
of
the rotational speed vector {(Ok} for
the locally occurring rotation
of
a fluid element per time unit can be stated as
follows:
. R
au
.-
20
=
2(01.
=
--
L::.. /"o((U)
Ij
J{"'I
.
ox)
The quantity
(Ok
states the double rotational speed
ofthe
axis
of
the fluid
element occurring
in
positive direction. The second diagonal
of
the considered
tluid element rotates with the same angular speed.
{(Ok}
is
an important
kinematic quantity
of
the velocity field.
It
is defined as swirlinglrotational
power (Wirbelstrke) and
is
computed as
half
the rotation
of
the velocity field.
Thus it is a field quantity
of
its own
(Ok
(Xi' t), for which holds:
(Ok(x
i
,
t) = ° when a flow field is free
of
rotation.
When
(Ok(x
i
,
t)
'*
0,
flows subjected to rotations are present, whose
swirling properties are best accessible when expressing the conservation laws
for mass, impulse and energy in
(Ok'
aU
1
-"\-
(6x
2
)9>M
oX
2
'"
~I
I"
~0~
~'~'~
Ll
2 t / '
...
-r-!
6x
60
1
2
aU
2
6x
1
--(6x)M
aX
1
1
x
=x
2 J
x
=x
1 1
Fig. Translation and Angle Deformation
of
~
Fluid Element
in
a
rlow
Field due to Velocity Gradients
x
=X
1 1
Fig. Elongation
ofa
Volume Element due to Velocity
Gradients
in
the Flow Field
When one considers next the angle deformation
of
a fluid
element,
one
can see that for the angle deformation holds:

Basics
of
Fluid Kinematics
89
e
·
D21
=
-2~(ddetl
- dd0,2)
Deformation angular speed
Thus
for the angular deformation in the plane x I - x
2
holds generally
e~l
=~(au'l:..+
au
l
.)
L 2 aXI aX2
Or
generally:
e
D
=
~(auj
+
au!)
1]
2
aX
i
aXj
i*i
Analogous to considerations in solid-state mechanics
the
symmetry
of
the
deformation tensor holds:
eP=eP
1] 1]
Finally
one has
to
consider
the
dilatation
of
a
fluid
element
which
experiences strain rates
due
to
the velocity gradient existing in a flow field.
The
linear deformation/change in length occurring due to an existing velocity
gradient in direction
Xl
can
be
stated as follows:
dl
_
1.
(au
l
)
(oxlh
ilt
_
(au
l
)(S::
)
- -
1m
--
-
--
uXI
9\
dt
t.HO
ax]
ill
aXI
From this is
computed
the
linear deformation occurring
per
length and
time
unit:
1
d(ll)
aU
I
-----=--
(Llx
l
)
dt
aXI
When multiplying
the
linear deformation
with
the transverse area the
apper-taining volume
change
results:
d(oVjh =
(au]
)(OV,)
dt
aXI
1
~
Summed up over all three axis directions one obtains for the entire volume
change
per
time
unit:
1
d(oVh
i)U
i
---
=--
(OV)9\ dt i)xi
i.e. the divergence
of
the velocity field indicates
how
the
volume
of
a
fluid element at a point in space changes
with
time.
It
is customary in literature to
combine
elongations
offluid
elements and
their angular deformations
to
a deformation
tensor
in such a
way
that it holds:
_ 1
(au
j
au!)
c
Y
-"2
aXi
+aXj
fori*i

90
Basics
of
Fluid Kinematics
so that for the deformation tensor holds:
{Eij}
=
f:~:
:~:
:~:}
und Eij = Eij
E3}
E32 E33
From the above considerations the following relation results:
aU
j
=~(aUj
+
aUj)+~(aUj
+
au
j
)
ax;
2
ax;
aXj
2
ax;
aXj
i.e. it holds:
R
au·
de..
1
au·
}
I)
}
-:1-
=
Eij
+
-""1-
= Eij +
-Eyk
-""1-
oX
j
oX
j
2
oX
j
The gradients existing in velocity fields are linked to deformations and
rotations
of
fluid elements, the gradients allowing to state corresponding rates
of
deformation (normalized deformation per unit time) and rotational angle
velocities. This has to be considered when employing the analogy between
solid-state mechanics and fluid mechanics, in order to transfer considerations
on deformations
of
elastic bodies, carried out in solid-state mechanics to rates
of
deformation
of
fluid elements occurring in fluid mechanics, due to existing
gradients
of
the flow field.
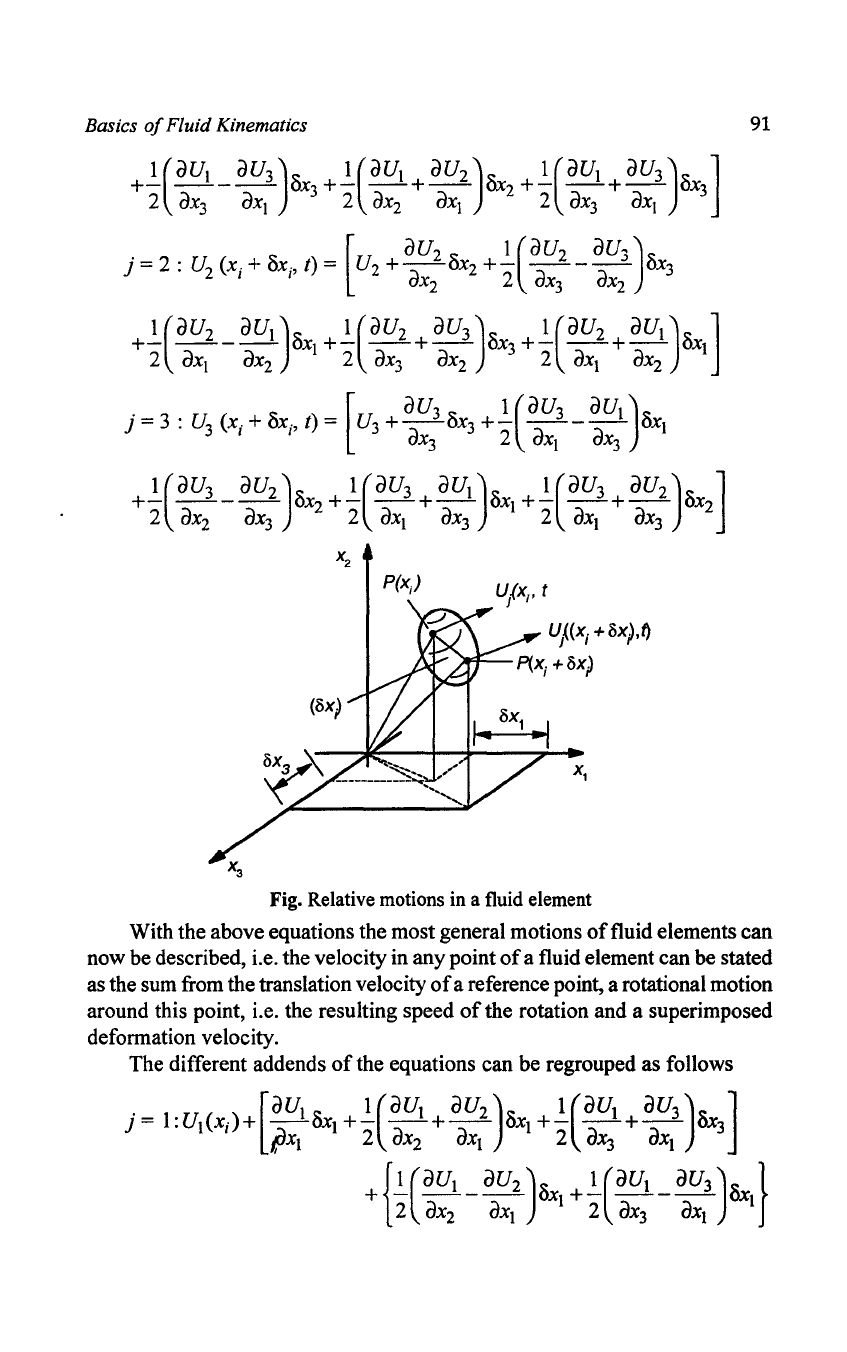
Relative Motions
Considerations
of
the velocities at two points separated by (dx
i
)
result in
the following relation:
au·
U.(x.
+
Ox.
t) =
Uj(Xj,t)+~OXj
+
...
}'
p
~
or transcribed:
Rotation
.
'1
(aU
j
au.)
, 1
(aU
j
au.)
U·(x·
t)+-
----,
ox·+-
----,
ox·
~
2
aXi
aXj
'2
aXi
aXj
,
Translation
'v
'
Defonnation
This relationship makes it clear that the velocity at the adjacent point
Xi
+Ox
i
is composed
of
the translation by velocity at point p(x
i
),
a rotational
velocity around this
point
and a deformation velocity in this point.
The
components for j =
1,2,3
read:
J = 1 : U
l
(Xi
+
UX
i
,
t)
= U
l
+--OXI
+-
-----
OX2
.
~
[au}
1
(aU
l
au
2
)
ax}
2
aX2
ax}
Basics
of
Fluid Kinematics
91
Fig. Relative motions
in
a fluid element
With the above equations the most general motions
of
fluid elements can
now be described, i.e. the velocity in any point
of
a fluid element can be stated
as the sum from the translation velocity
of
a reference point, a rotational motion
around this point, i.e. the resulting speed
of
the rotation and a superimposed
deformation velocity.
The different addends
of
the equations can be regrouped as follows
} =
I:UI(x;)+
-
8X
I
+-
-+--
8XI
+-
-+--
8x3
.
raUl
I
(aU
I
au
2
)
1
(aU
I
au
3
) ]
jJXI 2 aX2 aXI 2
aX3
aXI
+{!(aU
I
_
aU
2
)
8x
I
+!(aU
I
_
aU
3
)&1}
2
aX2
aXI 2
aX3
aXI
