Brewster H.D. Fluid Mechanics
Подождите немного. Документ загружается.


•
62
Physical Basics
of
Fluid
following relation holds, when the fluid element 9i is located at the time t at
position
xi:
dam
aa aa
Da
am(t)=a(x·,t)---=-+U-=-
'"
I dt at I
Ox.
Dt
I
The second part
of
equation states how temporal changes
of
substantial,
thermodynamic quantities can be computed from the substantial derivative
of
corresponding field quantities.
In addition to the above introduced thermodynamic state properties
P
9t
, T
9t
,
P9t'
e
9t
, ... , other state properties can be defined whose introduction is
of
advantage in certain thermodynamic considerations. Some
of
them are:
1
• Specific volume:
um
=-
Pm
• Enthalpy:
~
=
em
+
P9illm
• Free energy:
f9i
=
em
-T
9i
s
9i
(Helmholtz potential)
• Free enthalpy:
g9i
=
~
- T
9i
s
9i
(Gibb potential)
Accordingly, it
is
possible to apply certain mathematical operators in order
to define
"new" thermodynamic quantities. However, their introduction makes
sense only when advantages result from the introduction into the thermody-
namic considerations that are to be carried out with the new quantities.
In one
of
the above definitions for thermodynamic potentials, the entropy
was used whose definition is given by a differential relation:
T9i
ds
9i
=
dem
+
P9i
d
llm
(Gibb relation)
Integrating one obtains:
sm
=
s(91)o
+ f91 _l-dem +
f9l
PjR
dUm
~e91)o
TjR
~U91)o
TjR
The above relations can be understood as identical definition
of
equations
for the entropy
s
of
a fluid element. When employing the relation one obtains
with
ds
m
= Ds
dem
=
De
and
dUm
=um
aU
i
3
dt Dt dt dt dt
Oxi
the following relation:
r;
ds
m =
dejR
+ R
dUm
m dt dt m dt
or:
T(as
+U;
as.)=(ae
~u;~)+
p(au;)
at
Oxi.
at
ax;
p
aXi

Physical Basics
of
Fluid
63
When one applies the mass conservation equation
of
the law
of
differential
equations, it can be rearranged further:
(
8Ui)
__
!~
8x;
pDt
of
the mass conservation equation inserted in yields:
TDs
_De
PDp
Dt - Dt -
p2
Dt
From this relation further relations can be derived that are
of
importance
for fluid mechanics considerations, e.g. for
s:R
= const.:
(:),
~;,:
~(d::
L
~
~
~(:~L
For
P:R
= const.
or
u:R
= const it holds:
T(~;)p ~(~;)p
~T"
~(~:t
It holds further for
e:R
= const.:
T(DS)
=_
~(DP)
~P91
=T91(
8S
91)
=_T91P~(8S91)
Dt e p Dt e
8u91
e91
8P91
e91
Further significant relations known from thermodynamics are needed in
the following:
• Specific heat capacity
of
a fluid at constant volume
c _ (
8e
91
) =
T91
(
8S
91
)
v -
8T91
u91
8T91
u91
• Specific heat capacity
of
a fluid at constant pressure
c _
(8
hn
) =
T91
(
8s91
)
p -
8T91
P9l
8T91
P9l
where
is
h:R
=
e9t
+
P:R
'\}:R
• Isothermal compressibility coeffcient
I
(8u
91
) I
(8
P
91
)
a = -
u91
8P
91
T91
=
p91
8P
91
T91
• Thermal expansion coeffcient
1
(8u
91
) 1
(8
P
91
)
~
=
u91
8T91
P9l
= -
P91
8T91
P9l
When one takes into consideration that the following relation holds
d -
(8
P
91
)
dT91
+
(8
P
91
)
dP
91
p:R
-
8T91
P9l
8P
91
T91

64
Physical Basics
of
Fluid
the following relation can be formulated for all fluids:
1
-dp~
=
o.dP~
=
f3dT~
p~
Or rearranged in terms
of
field variables:
!...
Dp = a
DP
_ P
DT
pDt
Dt
Dt
This relation allows the statement that all fluids
of
constant density, i.e.
fluids having the property
p~
= const. or (DplDt) = 0, can be designated as
incompressible. They react neither
to
pressure variations
(a
= 0) nor to
temperature variations
(~
= 0) for changes in volume or density.
For any fluids, the difference
of
the heat capacities results:
(c _ c ) =
T~
f32
= _
T~
.
f3(
ap~
) =
T~
(ap~
)
(au~
)
p u
P~H
a
p~
aT~
p~
aT~
p~
aT~
P9l
The above general relations can now be employed to derive the special
relations that hold for the two thermodynamic ideal fluids that receive special
attention in this manual, namely the ideal gas and the ideal fluid. For an ideal
gas holds
P~
-R
T P
- -
1.
~
consequently - = RT
p~
P
and in addition
(~~
) =
(:~~
) = 0 and C
v
= const, i.e. the internal
~
T~
~
T~
energy
of
an ideal gas is a pure function
of
the temperature. For the isothermal
compressibility coeffcient a and the thermal expansion coeffcient
~
yields
1
(ae
w
)
=_1
__
1_=_1
a =
p~
ap~
T~
p~
RT~
P~
1
(ap~)
1 (
P~
1 1
~
= -
p~
aT~
P9l = -
p~
RT~
=
T~
and thus for the difference
of
the specific heat capacities:
=
T~
~2
P~
=-.!JL=R
c
p
-
C
v
p~
T~
p~T~
It
can further be formulated for the change in density:
dp~
dP~
_
dT~
p~
P~
T~
As a further fluid
of
significance, we introduce the thermodynamic ideal
liquid that distinguishes itself by
a = 0 and
~
=
0,
i.e.

Physical Basics
of
Fluid
dPm
=0
(fluid
of
constant Density)
Pm
For the difference
of
the heat capacities
it
can be computed:
c - c
= -
Tm
A
(ap
m
)
bei
A = 0
......;
c = c .
p u I-'
aTe.
I-' p u
Pm
m P9t
When one employs the. Gibb relation,
dp'.)t
=
du'.)t
= 0 yields:
(!::L
=;~
65
Because
s'.)t*
s'.)t
(P'.)t),
the pressure in an ideal liquid is not taken into
account as a thermodynamic quantity. It exists as a mechanical quantity,
however, for an ideal fluid it
is
not part
of
a thermodynamic state equation.
A further physical property
of
a fluid, which is
of
significance when deal-
ing with some
of
the flow problems presented in this book, is the velocity
propagation
of
small pressure perturbations, the so-called sound velocity:
c
2
=
(:::lm
This quantity
is
defined as pressure modification due to the changes
in
density, the entropy being maintained constant, i.e. the propagation
of
small
acoustic perturbations takes place isentropically.
When one takes into account the following relation for the cited sequence
of
partial derivations
and"
if
one considers
it holds:
C
v
=
Tm(:~m)
m P9t
When taking into account the Maxwell relations
(
aTm)
1
(aPm)
apm
S9t
=
p~
aS
m
P9t
(
apm)
2
(aTm)
aS
m
rm
=
-Pm
ap
m
P9t
66
Physical Basics
of
Fluid
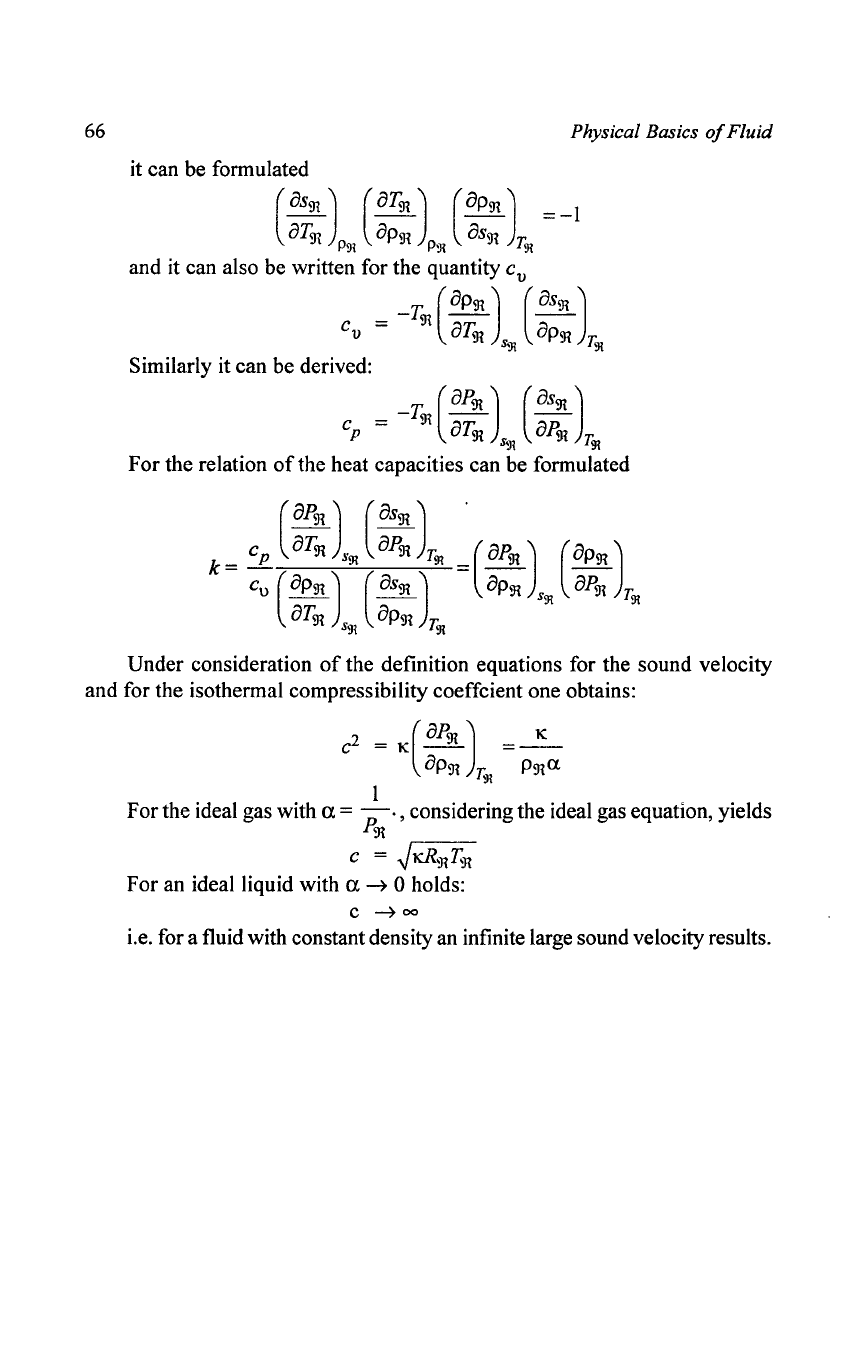
it can be formulated
(
8sm
) (8rm )
(8
p
m
) =
-1
8r
m
8Pm
8s
m
7'
P91
P91
191
and it can also be written for the quantity
clJ
_
-Tm
(8
p
m
)
(8S
m
)
clJ
- 8T
m
S91
8Pm
T91
Similarly it can be derived:
_
-Tm
(8P
m
) (8S
m
)
c
p
-
8T
m
S91
8P
m
T91
For the relation
of
the heat capacities can be formulated
Under consideration
of
the definition equations for the sound velocity
and for the isothermal compressibility coeffcient one obtains:
c
2
=
K(
8P
m
)
= K
8Pm
7'
Pm<X
191
I
For the ideal gas with
a.
=
Pm"
considering the ideal gas equation, yields
C =
~KRmTm
For an ideal liquid with
a.
-7
0 holds:
c
-700
i.e. for a fluid with constant density an infinite large sound velocity results.

Chapter 3
Basics
of
Fluid
Kinematics
GENERAL
CONSIDERATIONS
The the most important basic knowledge
of
mathematics and physics with
respect to fluid mechanics. This knowledge is needed to describe fluid flows
or
derive and construct basic equations
of
fluid mechanics in order to solve
flow problems.
Here it is important to know that fluid mechanics is primarily interested
in the velocity field
~(Xj'
t) at initial and boundary conditions, and in the
accompanying pressure field
P(x
j
,
t), i.e. fluid mechanics tries to describe
flow processes in field variables.
This representation results in
"Eulerian presentation"
of
fluid flows. This
is best suited for the solution
of
flow problems and is thus applied in
experimental, analytical and numerical fluid mechanics. The introduction
of
field quantities for the thermodynamic properties
of
a fluid, like e.g. the
pressure
P(x
j
, t),
the temperature T(x
j
, t),
the density p(x
j
, t),
the internal energy
e(xj' t) as well as for the molecular transport quantities, as the dynamic viscosity
!l(x
j
,
t), the heat conductivity A(x
i
, t) and the diffusion coefficients
D(xi'
t) so
that a
complet\":
presentation
of
fluid mechanics is possible.
With the inclusion
of
diffusive transport quantities, i.e. the molecular heat
trans-port
q,{Xj'
t), the molecular mass transport
m,{x,.,
t) the molecular momen-
tum transport
tj/Xi' t), it is possible to formulate the conservation laws for
mass, momentum and energy for general application.
The basic equations
of
fluid mechanics can thus be formulated locally,
and hold for all flow problems in the same form. The differences in the
solutions result from the different initial and boundary conditions that define
the actual flow problems which enter into the solutions by the integration
of
'the locally formulated basic quations.
Experience shows that the derivation
of
basic equations
of
fluid mechanics
can be achieved in the easiest way
if
considerations are carried for fluid ele-
ments, i.e. by employing the
"Lagrangian consideration" for the derivation
of
equations. The "Lagrange considerations" assumes that a fluid can be split up

68
Basics
of
Fluid Kinematics
at a fixed time t = 0, in "marked elements" with the mass
8m
9\ ' the pressure
P 9\ ' the temperature T 9\ ' the density P 9\ ' the internal energy e 9\ etc. The
element with the index
9\ possesses also a velocity
(U)9\'
which is defined as
Lagrangian
velocity and which is always linked to the fluid element marked
Basics
of
Fluid Kinematics once with as well as to all other quantities labelled
with
9\.
In fluid mechanics, these are also designated as substantial quantities and
always employed to derive the basic laws
of
fluid mechanics in an easily
comprehensible way.
As the following considerations will show, the basic knowledge
of
mechanics gained in physics can be transferred in the most simple way into
fluid
mechanics
by
deriving
the
basic
equations
for fluid
elements
by
introducing the Lagrange considerations.
SUBSTANTIAL
DERIVATIVES
While one defines a generally as a substantial quantity, the derivation
of
fluid mechanics equations often require the total differential da to be employed.
80.
80. 80. 80.
do.~
=-dt+-(dx!)lR
+-(dx2)~
+-(dx3)~
8t
8xl
8x2 8x2
Fluid element
(at time t)
\
Fluid element
(at time t
+ dt)
Fig. Motion
of
a Fluid Element in Space
The fluid element motion in space can be described as follows:
(dx
l
)
=
(U
I
)
dt = Uldt
(dx
2
)
=
(U
2
)
dt = U
2
dt
(dx
3
)
=
(U
3
)
dt = U
3
dt
The transition
of
substational velocities (0;)9\ to
the
field quantities U
j
in
equation is permissible, as at the time
I(X
j
)
= x,{I) and thus (U;) (I) = U,{Xj' t).
Therefore generally it holds:
80.
80. 80. 80.
do.~
=
-dt
+
-U
l
dt-U
2
dt
+
-U
3
dt
8t
8x! 8x2
8X3

Basics
of
Fluid Kinematics
and for the substantial time derivative with
a~
(I) =
a(x
i
'
t)
when
x~=
xi at the time t it holds:
da~
=
oa
+U
j
oa
=:
Oa
dt
at
OXj
Dt
69
where (DaIDt) is the substantial time derivative
of
the field quantity
a(x
j
,
t) with respect to time and the operator:
~:=~+U.~
Ot
at
'ax·
I
indicates how the substantial derivative
of
a field variable is to be
calculated. The operator
DlDt may only be applied to field quantities. When
one applies
DlDt to the velocity field
~(xi
' t), the substantial acceleration
results, i.e. the local acceleration which a fluid element experiences in a flow
field at a point
Xj
at time t where
~
(xi'
t) exists.
DU·
au·
au·
__
I =
__
,
+u
j
--'
Dt
at
OXj
The substantial derivative plays an important role in the derivation
of
the
momentum equation
of
fluid mechanics
in
Euler variables.
In
the acceleration
term in Euler variables, four partial derivatives occur per momentum direction
j =
1,2,3,
one time derivative and three derivatives with respect to the space
coordinates
xI'
x
2
and
x3
i.e. the spatial derivatives
(a~
lax;)
multiplied by U
i
occur in the substantial acceleration. These nonlinear terms
in
the resulting
momentum equations lead to mathematical complications when flow problems
are to be solved.
They prevent the application
of
the superposition principle
of
solutions,
result
in
solution bifurcations, i.e. in multiple solutions for equal initial and
boundary conditions and in coupled velocity fluctuations, e.g. in turbulent
flows. The treatment ofthese nonlinear terms
is
considered in the presentations
of
this book. It is important that their significance is understood in detail as
part
of
the acceleration term
of
fluid elements. It is important to realise that
not only the temporal changes
of
the velocity field that lead to accelerations
of
fluid elements, but also the motion
of
a fluid element in a non-uniform
velocity field.
MOTION
OF FLUID
ELEMENTS
Flow kinematics is.a .vast field and a comprehensive treatment, which is
meant to give only an introduction into sub-domains
of
fluid mechanics, among
others also into fluid kinematics.
To such an introduction belongs the treatment
of
path lines
of
particles,
i.e. the computation
of
space curves along which marked fluid elements move
in a fluid. Further, the computation
of
sweeping paths shall be treated, i.e. the

70
Basics
of
Fluid Kinematics
"marked path" is to be computed which leaves a fixed injected tracer in a
flow field. Both, the computation
of
path lines and
of
sweeping paths is
of
importance for the entire experimental flow mechanics, where it is often tried
to get an insight in the process
of
flows by observations
or
also by quantitative
measurements
of
the temporal changes
of
position
of
'''flow
markers"'.
Path
Lines
of
Fluid
Elements
When one subdivides at the time t = 0 the entire domain
of
a flow field
that is
of
interest into fluid elements and when one states the space coordinates
of
the mass centers
of
gravity
of
the each element in a coordinate system
at
the time t = 0, one achieves a marked fluid domain such that the position
vector
9t:
{
Xj
}9t,
0 = {
Xj
(t =
O)}
}9t
is assigned to a fluid particle. Each
of
the moving fluid particles, reSUlting
from the subdivision, marked and moving for -
00
< t < +
00
is defined as a
fluid element, that keeps its identity
0
:::;
t <
00
forever.
When kinematic considerations are carried out, only the motions
of
the
in-dividual fluid elements are
of
interest. These considerations result for each
fluid element in a separate and for the marked element characteristic path line.
The computation
of
these path lines will be explained in the following. Here
it is assumed that the flow field determining the fluid element motions is known.
As the velocity
of
a fluid element is only time-dependent, it follows from
d {
Xj
}9t
Idt =
{U
j
}9t
' that as a path line
of
a fluid element the frequency
locus:
t{X
j
(t)}9t =
{x;}!R,O
+
J~
{Uj(t')}!Rdt '
is to be understood. The position vector defined in this way for each
moment in time
t contains as a parameter the position vector
of
the particle
defined
at
the time t = 0 i.e. 9t, i.e.
{xl
}9t,O.
Now
the identity {U;} =
{U
j
}
can
be introduced into the considerations, i.e.
at
a certain moment in time t holds:
d{xj
}R
= {U.}", =
{U.}
dt
I:n.
I
The equals sign between the substantial velocity
{U;}9t
and
{U;}
existing
at
the moment in time t indicates that the identity
{x;}9t
= {x;} which exists
at
time t justifies equating the substantial velocity
{U
j
}9t
with the field size
{~}.
For
the components
{x;}9t
of
the particle motion it holds therefore:
d{xdR
{U.}
d{xilR =
U.
dt
I
or
dt I
These differential equations have to be solved for i =
1,
2, 3 in order
to
determine the path lines
of
fluid elements.
The
differential quotient. in the
relation states that as a solution
of
the above differential equation the path

Basics
of
Fluid Kinematics
71
line
of
a fluid element is obtained whose position was defined at the moment
:in
tinet
= 0 with
{xj}:R
o.
The general way or'proceeding when defining path lines will be explained
and made clear by the example stated below. The components
of
the flow
velocity field shall be given:
U
I
=
xI
(1
+ t), U
2
=
-x
2
und U
3
=
-x3
t
When one inserts these statements on the velocity field in the above
indicated differential equations for the path lines
of
a fluid element, one obtains:
d{Xl}~
=X
(l+t)
dt
1 ,
d{X2}~
---'-d....::t=-=-
= -
x2
,
and
d{X3}~
-x
t.
dt
3
This law
of
differential equations can be solved now and results
in
the
following solutions holding for the path lines
of
all fluid elements:
(Xl(t))~
=C
1
exp[t+ t;]
(x2(t))~
=C
2
exp[-t]
(X3(t))~
= C
3
ex
p
[-
t;].
When one considers a fluid element
of
interest which had the position
coordinates (1, I, 1)) at the time
t = 0, then from the initial conditions for each
of
the equations
in
the introduced constants C
a
result uniformly as:
C
I
= C
2
= C
3
=
1,
i.e. for the case considered here all integration constants are equal. For
the path lines
of
this fluid element yields:
xI
(t):R
= exp[t +
t:
] '
X
2
(t):R
=
exp[-t]
x3 (t) = ex
p
[-
t;
] .
This path line is presented spatially
in
Figure.
When one selects a particle whose position at time
t = 0 showed different
position coordinates, the integration constants
C!, C
2
,
C
3
change accordingly
and a different path line results. Thus the path line is an
"individual" property
of
a fluid element which
in
the resulting equations is determined by the flow
field and the position
of
the fluid element at the time t =
o.
