Brewster H.D. Fluid Mechanics
Подождите немного. Документ загружается.

102
Basic Equations
of
Fluid Mechanics
Because
of
the universal mass conservation in formulation, the last term
in equation is equal to zero:
d(OJ
j
)9t
d«U
j
)9t)
(au.
au.)
dt
=o~
dt
=o~
a/
+U
j
ax.'
I
This can be written as follows:
om9t
= po V
9t
applying
P9t
= p when:
(x9t(t))j =
Xi
at the time
t,
d(OJ
j
h =
poV9t
(aU
j
+ U
j
au
j
)
dt
at
aXi
Owing to the above derivations it is possible to state the left side
of
the
equation
of
momentum in field quantities. For the right side the below-cited
considerations can be carried out. The inertia forces can be represented in an
easy way by the acceleration vector,
~g},
i.e. by its components gj.
L(OM
j
)9t
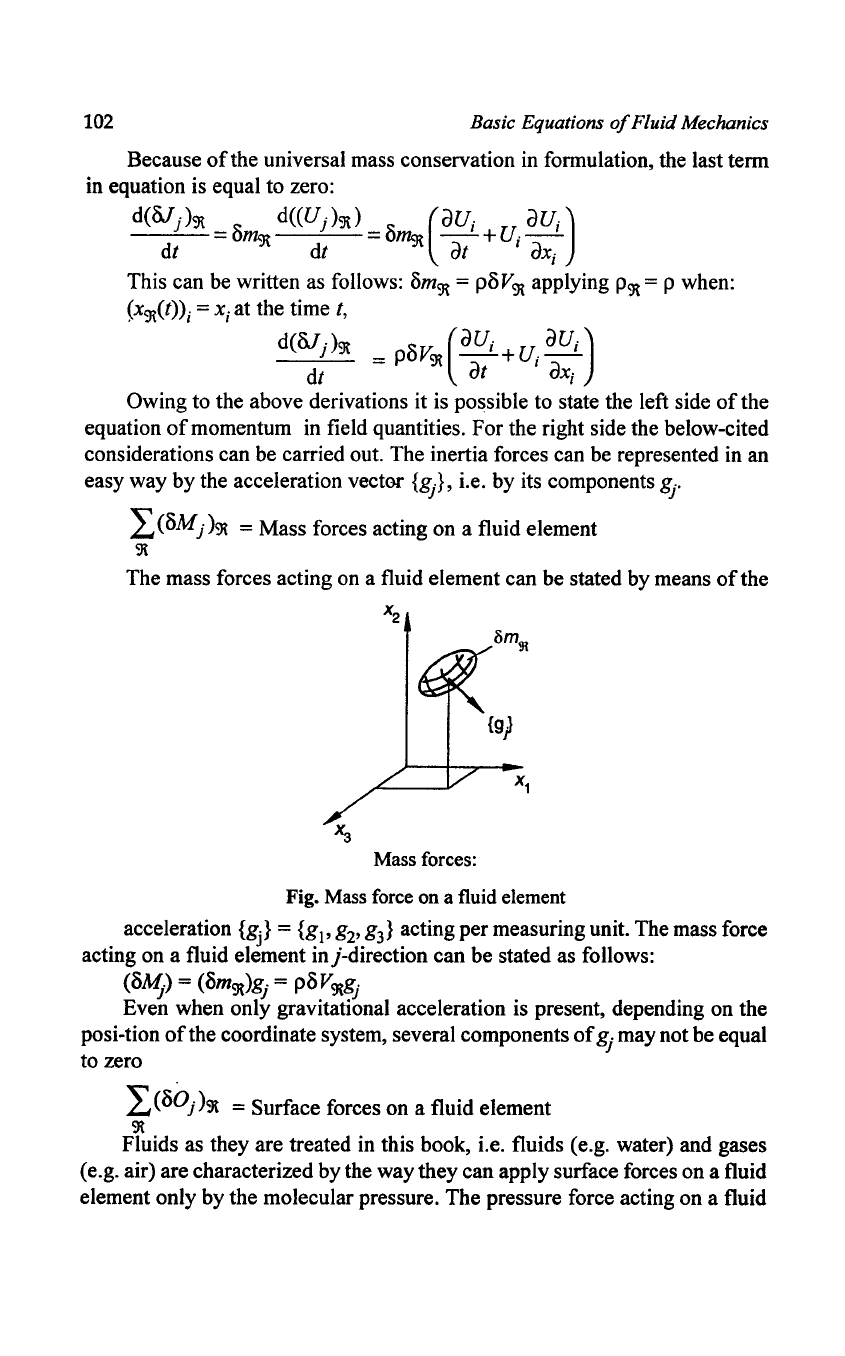
= Mass forces acting on a fluid element
~
The mass forces acting on a fluid element can be stated by means
of
the
x
2
Mass forces:
Fig. Mass force on a fluid element
acceleration
{g}
= {gl'
g2'
g3} acting per measuring unit. The mass force
acting on a fluid element inj-direction can be stated as follows:
(oA9
=
(om9t)gj
= poV
9t
g
j
Even when only gravitational acceleration is present, depending on the
posi-tion
of
the coordinate system, several components
of
gj may not be equal
to zero
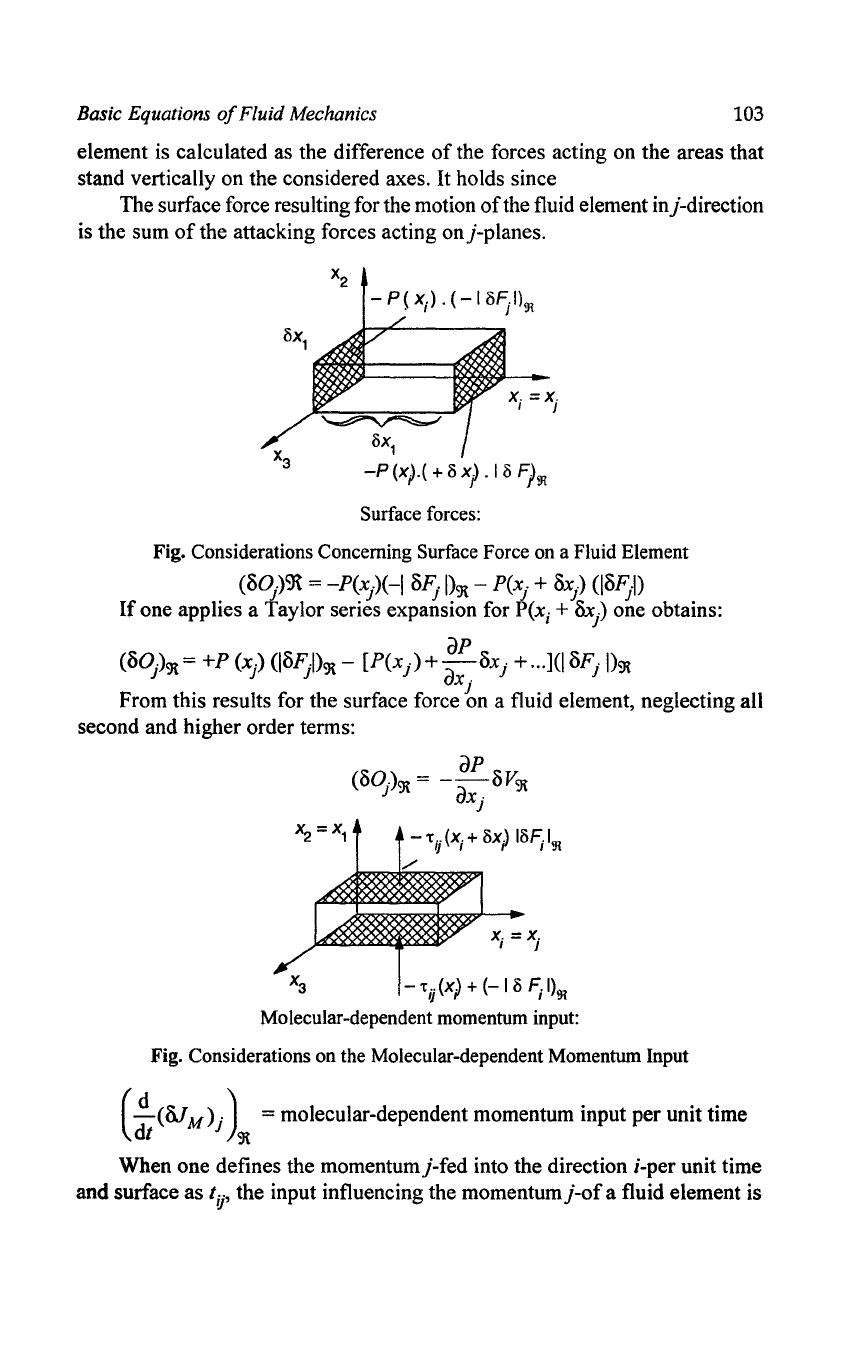
L (oOj)9t = Surface forces on a fluid element
9t
Fluids as they are treated in this book, i.e. fluids (e.g. water) and gases
(e.g. air) are characterized by the way they can apply surface forces on a fluid
element only by the molecular pressure. The pressure force acting on a fluid
Basic Equations
of
Fluid Mechanics
103
element is calculated as the difference
of
the forces acting on the areas that
stand vertically on the considered axes. It holds since
The surface force resulting for the motion
of
the fluid element in j-direction
is the sum
of
the attacking forces acting onj-planes.
-P(x.).(-loF.ll
m
. I J
:n
Surface
forces:
Fig. Considerations Concerning Surface Force
on
a Fluid Element
(OO.)~
=
-P(x)H
OFj
D9t
-
P(Xj
+
ox)
(lo~.I)
If
one applies a Taylor series expansion for P(x
i
+
Ox)
one obtains:
ap
(OO)9t=
+P
(x)
(lOFjD9t
-
[P(X
j
)
+ ax.
OX
j
+
...
](\
OF
j
D9t
From this results for the surface force
~n
a fluid element, neglecting all
second and higher order terms:
ap
(OO.)9t
=
--OV9t
) ax·
}
Xa
-
tq(x)
+
(-I
0
F;
I)!R
Molecular-dependent
momentum input:
Fig. Considerations
on
the
Molecular-dependent
Momentum
Input
(
,!(OJ
M )
j)
= molecular-dependent momentum input per unit time
dt
9t
When one defines the momentumj-fed into the direction i-per unit time
and surface as
tij'
the input influencing the
momentumj-of
a fluid element is

104
Basic Equations
of
Fluid Mechanics
calculated as an input
at
the position x; and as an output at the position (xi +
Ax;), i.e. it holds:
(
d(8J
M
)j)
dt . = -
'"C
ij
(x;)(
-I
8F)
Iht
-
'"C
ij
(x; +
Ax;
)(1
8F!
1)9\
)
By
a Taylor series expansion one obtains for the term
'"CU<x;
+ 8x):
(
d(8J
M
)j)
(J'"Cij
= +
'"CiJ
(XI
)(1
8F;
Iht
-
'"Cijo(x;
+
-8x
i
···](8F;)9\
dt
9\
ax;
This results in:
(
_d
C
_8J_
M
_)..::....j)
=
__
ch_ij
8
V9\
dt
9\
ax;
When one inserts all these derived relations after division by
8V9\
the
equation
of
momentum
of
fluid mechanics in direction} results, i.e. for} =
1,
2, 3 three equations result:
(
aU
j
au
j
)
ap
a'"Cij
p
--+U
i
--
=pgj----
at
aX
i
ax)
aXiJ
As in this equation the volume
of
the fluid element
8V9\
appearing in all
terms was eliminated, the equation
of
momentum hold per unit volume. The
momentum equation
in
the three coordinate directions results:
[
au)
U
au)
U au) u
au)]
p
--+
)--+
2--+
3--
at
ax)
aX2
aX3
ap
a'tI3 a't23
a't33
=
-----------+pg3
aX3
ax)
aX2
aX3
From the fluid mechanics point
of
view only for ideal fluids
'"Cij
= 0,
For fluids in general
'"Cij"#
° but for ideal fluids
in
terms
of
fluid mechanics

Basic Equations
of
Fluid Mechanics 105
'tij
=
O.
Hence the following forms
of
the momentum equations can be stated:
(
au)
au)
)
ap
a'tij
p
-+U
-
=----+pg
(.
Fl 'd )
at
I
ax;
ax)
ax;
} VISCOUS Ul e
(
au.
au.)
ap
p
a:
+ u
,
ax~
= - ax) + pg} (ideal Fluide)
THE
NAVIER-STOKES
EQUATIONS
In the above equation the molecular-dependent momentum input
'tij
occurring per surface and unit time,
is
an unknown term, i.e. it is introduced
formally in derivations, without details being considered, as it
can
be
formulated for several fluids. When one takes into consideration the symmetry
of
the term 'tif i.e. 1
'tij
1 = 1 'tJl
I,
holds, one notices/ascertains that there are the
following unknowns
in
the equations:
Ul'
U
2
'
U
3
'
P,
'tIl'
't
12
,
't
13
,
't
22
,
't
23
, 't33 =
10
unknowns
X2=x;
X3
Fig. Momentum input due to flow through the plane
oF)
For these unknowns there are only four partial differential equations, the
continuity equation and three equations
of
momentum, i.e. an incomplete
equation system exists that does not permit the solution
of
flow problems. It
is therefore necessary to state additional equations, i.e. to express the unknown
terms
'tfi physically well-founded, as functions
of
all;
/
ax;.
This is done below
for ideal gases,
as
their
properties
are
known
to
a large
extent
from
considerations in physics. From the below-stated derivations, relations for
'tij
= f
(all;
/
ax)
result, that are valid also for non-ideal gases and for a whole
class
of
fluids whose molecular momentum-transport properties can be
classified as
"'Newtonian'''. Thus the derived relations
'tij
are valid far beyond
ideal gases and represent in this book the basic equations to describe the
molecular-dependent momentum transport in Newtonian fluids.
When one considers a fluid element, one can see that the momentum
j
fed in direction i by a velocity field and can be stated as follows:
iij =
pull/6Fj
Assuming that the instantaneous velocity components are composed
of

106
Basic Equations
of
Fluid Mechanics
the velocity
of
the fluid flow U
i
and the share
of
the molecular motion u
i
one
obtains:
pUll
j
= p(U
i
+
Ui
)(U
j
+
Uj
)
= p(UiU
j
+uPj
+ujU
i
+UiUj)
By time averaging, one obtains for the time-averaged total momentum
change
of
the fluid element:
~~
--------
pUPj
=
p[UPj
+uPj
+ujU
i
+uiUj]
'--v---'
~
~
'-v--'
I
II
III
IV
The total momentum input consists
of
four terms that can be interpreted
physically as follows:
Term
I:
Momentum
inputj
in direction in i due to the velocity field
of
the Fluid.
Term
II:
Momentum
inputj
in direction i due to the molecular motion in
i-direction.
Term III: Momentum
inputj
in direction i due to the molecular motion in
j-direction.
Term IV: For i
*"
j is u
i
u
j
= 0 as the molecular motion in the three
coordinate directions - are not correlated; for i
= j results the pressure.
The molecular motion
is
distinguished by the presence
of
free path lengths
with finite dimensions, i.e.
I
*"
0,
the time averages
UiUj
and
ujU
i
are unequal
to zero. In order to calculate these contributions to
'tij
considerations on the
molecular momentum transport, ideal gases are recommended. For the number
of
molecules moving in direction
xi
and passing the plane A
in
Fig. 5.9
in
the
time
I1t
when ox} =
oX
2
=
oX
3
= a it can be written:
1 2
z. =
-na
u·l1t
I 6 I
Where n is equal to the number
of
molecules per unit volume,
a2
the
volume
of
area
oF
i
and u
i
the mean velocity
of
the molecules in direction
i.
Connected to
zi'
a mass transport through
oF
i
,
can be stated as follows:
A=oF
j
Xl
=X
j
oX
3
Fig. Momentum input in xi-direction with the molecular velocity u
j

Basic Equations
of
Fluid Mechanics
107
1 2
mz·
=
-(mn)a
U./lt
I 6'--v--' I
P
where m represents the mass
of
a molecule and thus can be set mn = p.
When one considers now the auxiliary planes
in
Figure located to dF
i
in
the distance
±l
and introduced for the derivations,
in
which the mean flow
field owns the velocity components
~(xi
+ I) and
~(Xj
-I).
In positive and
negative i-directions,j-directional momentum input and discharge can be stated
s follows:
{ij
= +
zim~
(xi
-I)
Momentum input over area
'OF
j
i~
=
-zim~
(Xj
+ I) Momentum discharge over area
'OF
j
Therefore the sum
of
the molecular-dependent input and discharge results:
Iliij =
zjm[~.
(xi
-I)
-
~.
(Xi
+ I)]
or
with
Zj
inserted from
equation:
1 2
Ili
..
=
-6
(mn)a
ujll/[Uj(xj-l)-Uj(xi+l)]
IJ
'-or--'
The momentum flow
pe~
unit area and time can be obtained by Taylor
series expansion
of
velocity at around
Xj
by neglecting the higher order terms:
II
1
Mij
1 [
aUj
aUj
]
'tij
= a
2
Ilt
='6
PU1
Uj(x
j
)-
aX
j
l-Uj(x
j
)-
aXj
I ,
so that for Term II in equation results:
II
1
aUj
aUj
'tij =
--pujl--
=
-ll--.
3
aXj aXj
Analogous to this it can be carried out considerations on
't~I
where for
Zj
can be written:
Fig. Momentum Input in xj-direction with Molecular
Velocity u
j
-and Fluid VelocityU
j

108
Basic Equations
of
Fluid Mechanics
In accordance with term III
in
equation a momentum inputj-results which
can be stated as follows:
r:
=
-zmU(x.
+ l)
1)
J , . J
or
t:..i..
=
zm[U(x.
-l)
- U (x. + l)]
1)
J , J ' J
Analogous to the derivations
in
equations yields:
i
lll
=
-.!.(pu
.f)
aU
i
=
-Il
aU
i
1)
3 J
ax·
ax.
'----v---"
J
Jl
For reasons
of
symmetry 'tij =
't
Ji
, so that u
i
= u
j
has to hold, i.e. the mean
velocity field
of
the molecules
is
isotropic (no preferred velocity direction),
so that it can be written:
for i
;to
j
This is the total
mom~ntum
input
'tij
for p = canst, i.e. when d/dt(oV
9t
) =
0,
the thermodynamic state equation for an ideal fluid is assumed. For p
;to
canst, an additional term needs to be added which
is
conditioned by the volume
increase
of
a fluid element. For the volume increase
of
a fluid element at point
xi
and time
t,:
d(oV
9t
) = (oV
9t
)
au,
dt
aXi
For the corresponding surface increase holds:
d(oF
9t
)
~(OF9t)
aU
i
dt 3
aXi
With surface increase an increased momentum input results:
2 aUk
't
y
=
+1l
3
0ij
aXk
This term has to
be
added
to
obtain general formulas
of
the
total
momentum input per unit time and unit area for ideal gases. It can be stated as
follows:
't
..
=_Il(aU
j
+
aUjJ+~o"1l
aUk
I)
ax;
ax} 3
I)
dXk
When one considers this relation for
'tij'
the basic equations
of
fluid
mechanics can be stated as follows:
Continuity equation:

Basic Equations
of
Fluid Mechanics
109
Momentum equations:
[
au.
au·
]
ap
a't··
. 1 1
IJ
(j=
1,2,3)
-+U
,
-
=----+pgl
at
aXi
aXj
aXi
For Newtonian fluids
'to =
-ll
__
+
__
'
+-0
ll--
[
au
j
au
1 2
aUk
I}
aX
j
aX
j
3
I}
aXk
With
'tij
from there exist equations for the 6 unknown terms
'tij
-in
the
momentum equations. The four equations, one continuity equation and three
Navier-Stokes equations, contain five unknowns:
P,
p,
~,
so that an incomplete
system
of
partial differential equations exists still. With the aid
of
the thermal
energy equation and the thermodynamic state equation valid for the considered
fluid, it
is
possible to obtain a complete system
of
partial differential equations
that permits general solutions for flow problems, when initial and boundary
conditions are present.
au
Continuity equation:
-a
1 = 0
xi
Navier-Stokes equations
(j
=
1,
2,
3):
[
au.
au.]
ap
a
2
u.
p
_1_+U
i
_
1
-
=-+ll--f-+Pgj
at
aXi
aXj
aX
i
This system
of
equations comprises four equations for the four unknowns
P,
U
1
' U
2
' U
3
. In principle, it can be solved for all flow problems to be
investigated, when suitable initial and boundary conditions are given. For
thermodynamic ideal fluids, i.e. p
= const, a complete system
of
partial
differential equations exists with the continuity equation and the momentum
equations, which can be used for solutions
of
flow problems.
MECHANICAL ENERGY EQUATION
In many domains
in
which fluid-mechanic considerations are carried out,
the mechanical energy equation
is
employed which can be derived from the
momentum equation} -For this purpose one multiplies equation with
~
:

110 Basic Equations
of
Fluid Mechanics
[
aUj
aUj
]
ap
a'tij
p U
j
-a-+U;Uj-a-
=-U
j
-a
-U
j
-
a
+Ujpgj
t
Xj
Xj
Xj
This equation can be transcribed as follows:
p[
:/~uJ
)+U
j
a~j
~uJ]
a(PU
j
)
aUj
a('tiju
j
)
aUj
a
+P---
+'tij-a-+pgjUj
Xj
aX
j
aX
j
XI
The equation states how the kinetic energy
of
a fluid element is changing
at a location due to energy-production and dissipation terms that occur on the
right side
of
the above equation. In order to discuss the significance
of
the
different terms, the following modification
of
the last term is carried out,
introducing a potential G from which the gravity is derived:
aG aG
f5;=
ax.
~pgjUj
=-Pax.
U
j
J J
Thus, employing
aG
= 0 :
at
pg-U.
=_p[aG
+U.
aG]=_pDG
J J
at
J
ax.
Dt
J
The combined equations yield for the temporal change
of
the kinetic and
potential energy
of
a fluid element:
D
(1
2 ) _
a(PU
j
)
aUj
a('tiju
j
)
aUj
p-
-U.
+G
--
+P---
+'tij--
Dt
2 J
aX
j
aX
j
aXj
aX
j
'-t~~~
Term I : This term describes the difference between input and discharge
of
pressure energy. Here it is referred to the considerations on ideal gases, in
the framework
of
which was shown that P =
~pu2
, i.e. expresses an energy
per unit volume. Therefore the following can be said:
(PU,{Xj»
= Input
of
pressure energy per unit area
-(P~{Xj
+
DXj»
= Discharge
of
pressure energy per unit area
Taylor series expansion and forming the difference yields for the energy
per unit volume:

Basic Equations
of
Fluid Mechanics
Term II: Considering:
the term:
aUj
= P d(oV
9t
)
aXj
OV
9t
dt
111
proves to be the work done during expansion, occurring per unit volume.
Term
III:
When taking into consideration that
tij
represents the molecular-
dependent momentum transport per unit area and unit time into a fluid element:
a('t
..
u.
)
a
lJ
} =
difference
from
the
molecular-dependent
input
and
Xj
discharge
of
the kinetic energy
of
the fluid.
au·
Term IV: The term 't
ij
-a
} describes the dissipation
of
mechanical
Xi
energy into heat. The above presentations show that the mechanical energy
equation can be derived from the
j momentum equation
by
multiplication with
~.
It
is to make sure that no independent equation and should be employed
along with the
momen'tum equation for the solution
of
fluid-mechanical
problems.
A special form
of
the mechanical energy equation
is
the Bernoulli equation
which can be derived from the general form
of
the mechanical energy equation:
D ( 1
2 )
ap
a'tij
p Dt
"2
U
j + G = -
ax
. U j -
ax.
U j
} I
ap
For
't
ij
= 0 and at =
0,
as well as p = const. Holds:
pE..[~U~+GJ=-prd~
+ua(~)]=
D~
Dt
2 } at }
ax
j Dt
D[l
2
P]
1 2 P
p-
-U.
+-G
=o--u.
+-+G
= const
Dt
2 } P 2 } P .
This form
of
mechanical energy equation can be employed in many
engineering applications for an imputation estimate
of
flow processes.
THERMAL
ENERGY
EQUATION
The
mechanical
energy
equation
is derivable from the momentum
equation, so that both equations have to be considered as not being independent
