Brealey, Myers. Principles of Corporate Finance. 7th edition

Подождите немного. Документ загружается.

Brealey−Meyers:

Principles of Corporate

Finance, Seventh Edition

II. Risk 8. Risk and Return

Companies, 2003

CHAPTER 8 Risk and Return 217

dex. The index has an expected return of 14 percent, and its standard deviation is 16

percent.

a. Suppose Percival puts all his money in a combination of the index fund and

Treasury bills. Can he thereby improve his expected rate of return without

changing the risk of his portfolio? The Treasury bill yield is 6 percent.

b. Could Percival do even better by investing equal amounts in the corporate bond

portfolio and the index fund? The correlation between the bond portfolio and the

index fund is ⫹.1.

11. “There may be some truth in these CAPM and APT theories, but last year some stocks

did much better than these theories predicted, and other stocks did much worse.” Is this

a valid criticism?

12. True or false?

a. Stocks of small companies have done better than predicted by the CAPM.

b. Stocks with high ratios of book value to market price have done better than

predicted by the CAPM.

c. On average, stock returns have been positively related to beta.

13. Some true or false questions about the APT:

a. The APT factors cannot reflect diversifiable risks.

b. The market rate of return cannot be an APT factor.

c. Each APT factor must have a positive risk premium associated with it; otherwise

the model is inconsistent.

d. There is no theory that specifically identifies the APT factors.

e. The APT model could be true but not very useful, for example, if the relevant

factors change unpredictably.

14. Consider the following simplified APT model (compare Tables 8.3 and 8.4):

Expected Risk

Factor Premium

Market 6.4%

Interest rate ⫺.6

Yield spread 5.1

Factor Risk Exposures

Market Interest Rate Yield Spread

Stock (b

)(b

)

P 1.0 ⫺2.0 ⫺.2

1.2 0 .3

.3 .5 1.0

Visit us at www.mhhe.com/bm7e

Calculate the expected return for the following stocks. Assume r

⫽ 5 percent.

15. Look again at Practice Question 14. Consider a portfolio with equal investments in

stocks P, P

, and P

a. What are the factor risk exposures for the portfolio?

b. What is the portfolio’s expected return?

16. The following table shows the sensitivity of four stocks to the three Fama–French fac-

tors in the five years to 2001. Estimate the expected return on each stock assuming that

the interest rate is 3.5 percent, the expected risk premium on the market is 8.8 percent,

EXCEL

Brealey−Meyers:

Principles of Corporate

Finance, Seventh Edition

II. Risk 8. Risk and Return

Companies, 2003

218 PART II Risk

1. In footnote 4 we noted that the minimum-risk portfolio contained an investment of

21.4 percent in Reebok and 78.6 in Coca-Cola. Prove it. Hint: You need a little calcu-

lus to do so.

2. Look again at the set of efficient portfolios that we calculated in Section 8.1.

a. If the interest rate is 10 percent, which of the four efficient portfolios should

you hold?

b. What is the beta of each holding relative to that portfolio? Hint: Remember that if a

portfolio is efficient, the expected risk premium on each holding must be

proportional to the beta of the stock relative to that portfolio.

c. How would your answers to (a) and (b) change if the interest rate was 5 percent?

3. “Suppose you could forecast the behavior of APT factors, such as industrial production,

interest rates, etc. You could then identify stocks’ sensitivities to these factors, pick the

right stocks, and make lots of money.” Is this a good argument favoring the APT? Ex-

plain why or why not.

4. The following question illustrates the APT. Imagine that there are only two pervasive

macroeconomic factors. Investments X, Y, and Z have the following sensitivities to these

two factors:

Factor Sensitivities

Factor Coca-Cola Exxon Mobil Pfizer Reebok

Market .82 .50 .66 1.17

Size* ⫺.29 .04 ⫺.56 .73

Book-to-market

†

.24 .27 ⫺.07 1.14

*Return on small-firm stocks less return on large-firm stocks.

†

Return on high book-to-market-ratio stocks less return on low book-to-market-ratio stocks.

CHALLENGE

QUESTIONS

Visit us at www.mhhe.com/bm7e

Investment b

X 1.75 .25

Y ⫺1.00 2.00

Z 2.00 1.00

We assume that the expected risk premium is 4 percent on factor 1 and 8 percent on fac-

tor 2. Treasury bills obviously offer zero risk premium.

a. According to the APT, what is the risk premium on each of the three stocks?

b. Suppose you buy $200 of X and $50 of Y and sell $150 of Z. What is the

sensitivity of your portfolio to each of the two factors? What is the expected

risk premium?

c. Suppose you buy $80 of X and $60 of Y and sell $40 of Z. What is the

sensitivity of your portfolio to each of the two factors? What is the expected risk

premium?

the expected risk premium on the size factor is 3.1 percent, and the expected risk pre-

mium on the book-to-market factor is 4.4 percent. (These were the realized premia from

1928–2000.)

Brealey−Meyers:

Principles of Corporate

Finance, Seventh Edition

II. Risk 8. Risk and Return

Companies, 2003

Visit us at www.mhhe.com/bm7e

d. Finally, suppose you buy $160 of X and $20 of Y and sell $80 of Z. What is your

portfolio’s sensitivity now to each of the two factors? And what is the expected risk

premium?

e. Suggest two possible ways that you could construct a fund that has a sensitivity

of .5 to factor 1 only. Now compare the risk premiums on each of these two

investments.

f. Suppose that the APT did not hold and that X offered a risk premium of 8 percent,

Y offered a premium of 14 percent, and Z offered a premium of 16 percent. Devise

an investment that has zero sensitivity to each factor and that has a positive risk

premium.

CHAPTER 8 Risk and Return 219

Brealey−Meyers:

Principles of Corporate

Finance, Seventh Edition

II. Risk 9. Capital Budgeting and

Risk

Companies, 2003

CHAPTER NINE

220

C A P I T A L

BUDGETING

AND RISK

Brealey−Meyers:

Principles of Corporate

Finance, Seventh Edition

II. Risk 9. Capital Budgeting and

Risk

Companies, 2003

LONG BEFORE THE development of modern theories linking risk and expected return, smart financial

managers adjusted for risk in capital budgeting. They realized intuitively that, other things being

equal, risky projects are less desirable than safe ones. Therefore, financial managers demanded a

higher rate of return from risky projects, or they based their decisions on conservative estimates of

the cash flows.

Various rules of thumb are often used to make these risk adjustments. For example, many com-

panies estimate the rate of return required by investors in their securities and then use this company

cost of capital to discount the cash flows on new projects. Our first task in this chapter is to explain

when the company cost of capital can, and cannot, be used to discount a project’s cash flows. We

shall see that it is the right hurdle rate for those projects that have the same risk as the firm’s exist-

ing business; however, if a project is more risky than the firm as a whole, the cost of capital needs to

be adjusted upward and the project’s cash flows discounted at this higher rate. Conversely, a lower

discount rate is needed for projects that are safer than the firm as a whole.

The capital asset pricing model is widely used to estimate the return that investors require.

states

We used this formula in the last chapter to figure out the return that investors expected from a sam-

ple of common stocks but we did not explain how to estimate beta. It turns out that we can gain some

insight into beta by looking at how the stock price has responded in the past to market fluctuations.

Beta is difficult to measure accurately for an individual firm: Greater accuracy can be achieved by

looking at an average of similar companies. We will also look at what features make some investments

riskier than others. If you know why Exxon Mobil has less risk than, say, Dell Computer, you will be in

a better position to judge the relative risks of different capital investment opportunities.

Some companies are financed entirely by common stock. In these cases the company cost of cap-

ital and the expected return on the stock are the same thing. However, most firms finance themselves

partly by debt and the return that they earn on their investments must be sufficient to satisfy both

the stockholders and the debtholders. We will show you how to calculate the company cost of capi-

tal when the firm has more than one type of security outstanding.

There is still another complication: Project betas can shift over time. Some projects are safer in

youth than in old age; others are riskier. In this case, what do we mean by the project beta? There

may be a separate beta for each year of the project’s life. To put it another way, can we jump from

the capital asset pricing model, which looks one period into the future, to the discounted-cash-flow

formula for valuing long-lived assets? Most of the time it is safe to do so, but you should be able to

recognize and deal with the exceptions.

We will use the capital asset pricing model, or CAPM, throughout this chapter. But don’t infer that

it is therefore the last word on risk and return. The principles and procedures covered in this chapter

work just as well with other models such as arbitrage pricing theory (APT).

Expected return ⫽ r ⫽ r

⫹ 1beta2 1r

⫺ r

221

In a survey of financial practice, Graham and Harvey found that 74 percent of firms always, or almost always, used the capital as-

set pricing model to estimate the cost of capital. See J. Graham and C. Harvey, “The Theory and Practice of Corporate Finance: Ev-

idence from the Field,” Journal of Financial Economics 60 (May/June 2001), pp. 187–244.

Brealey−Meyers:

Principles of Corporate

Finance, Seventh Edition

II. Risk 9. Capital Budgeting and

Risk

Companies, 2003

The company cost of capital is defined as the expected return on a portfolio of all

the company’s existing securities. It is used to discount the cash flows on projects

that have similar risk to that of the firm as a whole. For example, in Table 8.2 we

estimated that investors require a return of 9.2 percent from Pfizer common stock.

If Pfizer is contemplating an expansion of the firm’s existing business, it would

make sense to discount the forecasted cash flows at 9.2 percent.

The company cost of capital is not the correct discount rate if the new projects

are more or less risky than the firm’s existing business. Each project should in prin-

ciple be evaluated at its own opportunity cost of capital. This is a clear implication

of the value-additivity principle introduced in Chapter 7. For a firm composed of

assets A and B, the firm value is

Here PV(A) and PV(B) are valued just as if they were mini-firms in which stock-

holders could invest directly. Investors would value A by discounting its fore-

casted cash flows at a rate reflecting the risk of A. They would value B by dis-

counting at a rate reflecting the risk of B. The two discount rates will, in general, be

different. If the present value of an asset depended on the identity of the company

that bought it, present values would not add up. Remember, a good project is a

good project is a good project.

If the firm considers investing in a third project C, it should also value C as if C

were a mini-firm. That is, the firm should discount the cash flows of C at the ex-

pected rate of return that investors would demand to make a separate investment

in C. The true cost of capital depends on the use to which that capital is put.

This means that Pfizer should accept any project that more than compensates for

the project’s beta. In other words, Pfizer should accept any project lying above the

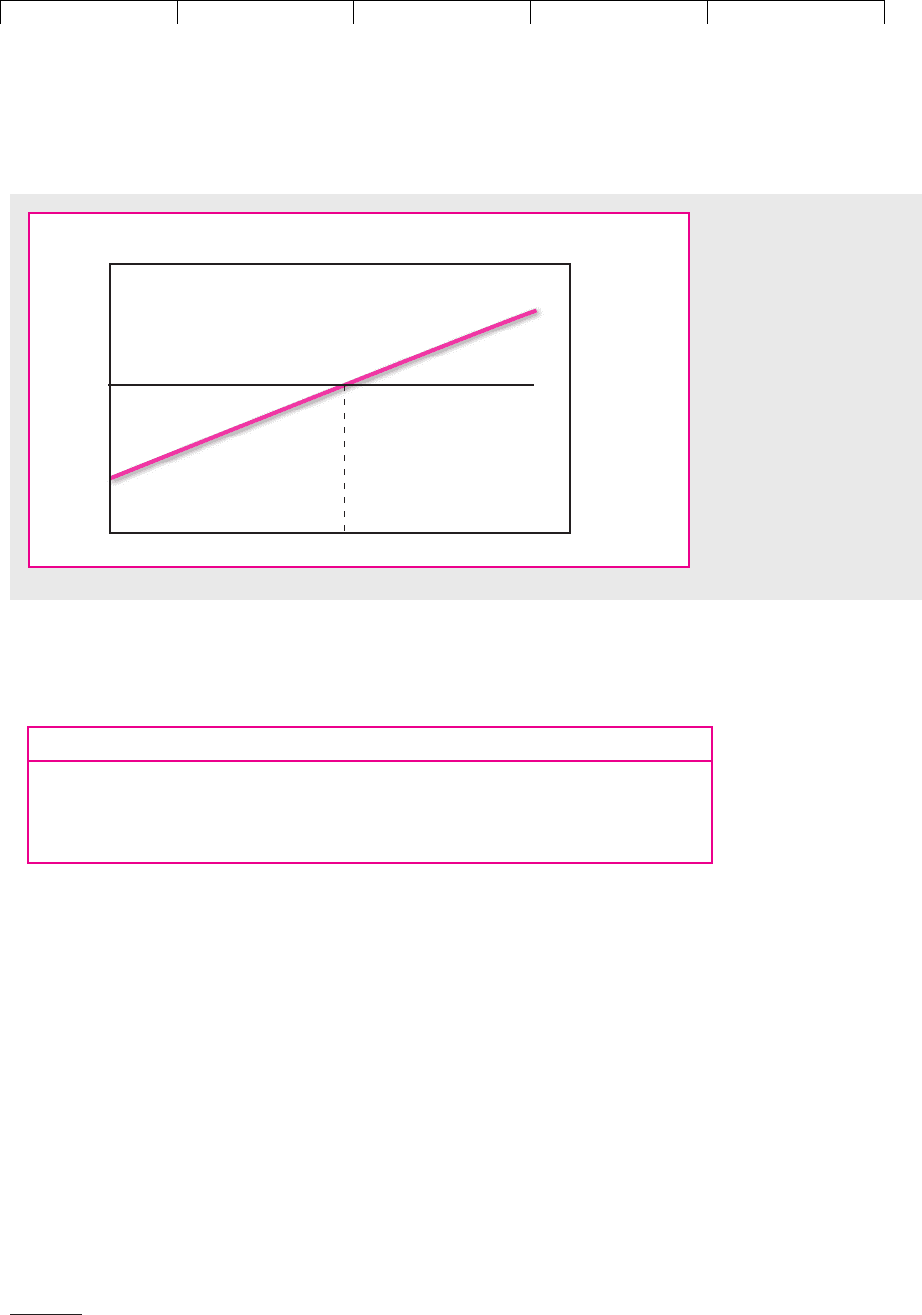
upward-sloping line that links expected return to risk in Figure 9.1. If the project

has a high risk, Pfizer needs a higher prospective return than if the project has a

low risk. Now contrast this with the company cost of capital rule, which is to ac-

cept any project regardless of its risk as long as it offers a higher return than the com-

pany’s cost of capital. In terms of Figure 9.1, the rule tells Pfizer to accept any proj-

ect above the horizontal cost of capital line, that is, any project offering a return of

more than 9.2 percent.

It is clearly silly to suggest that Pfizer should demand the same rate of return

from a very safe project as from a very risky one. If Pfizer used the company cost

of capital rule, it would reject many good low-risk projects and accept many poor

high-risk projects. It is also silly to suggest that just because another company has

a low company cost of capital, it is justified in accepting projects that Pfizer

would reject.

The notion that each company has some individual discount rate or cost of cap-

ital is widespread, but far from universal. Many firms require different returns

⫽ sum of separate asset values

Firm value ⫽ PV1AB2⫽ PV1A2⫹ PV1B2

222 PART II

Risk

9.1 COMPANY AND PROJECT COSTS OF CAPITAL

Debt accounted for only about 0.3 percent of the total market value of Pfizer’s securities. Thus, its cost

of capital is effectively identical to the rate of return investors expect on its common stock. The compli-

cations caused by debt are discussed later in this chapter.

Brealey−Meyers:

Principles of Corporate

Finance, Seventh Edition

II. Risk 9. Capital Budgeting and

Risk

Companies, 2003

from different categories of investment. For example, discount rates might be set

as follows:

CHAPTER 9

Capital Budgeting and Risk 223

Project beta

Company cost of capital

Security market line showing

required return on project

Average

beta of the firm's assets = .71

(required return)

3.5

9.2

FIGURE 9.1

A comparison between the

company cost of capital

rule and the required return

under the capital asset

pricing model. Pfizer’s

company cost of capital is

about 9.2 percent. This is

the correct discount rate

only if the project beta is

.71. In general, the correct

discount rate increases as

project beta increases.

Pfizer should accept

projects with rates of return

above the security market

line relating required return

to beta.

Category Discount Rate

Speculative ventures 30%

New products 20

Expansion of existing business 15 (company cost of capital)

Cost improvement, known technology 10

Perfect Pitch and the Cost of Capital

The true cost of capital depends on project risk, not on the company undertaking

the project. So why is so much time spent estimating the company cost of capital?

There are two reasons. First, many (maybe, most) projects can be treated as av-

erage risk, that is, no more or less risky than the average of the company’s other as-

sets. For these projects the company cost of capital is the right discount rate. Sec-

ond, the company cost of capital is a useful starting point for setting discount rates

for unusually risky or safe projects. It is easier to add to, or subtract from, the com-

pany cost of capital than to estimate each project’s cost of capital from scratch.

There is a good musical analogy here.

Most of us, lacking perfect pitch, need a

well-defined reference point, like middle C, before we can sing on key. But anyone

who can carry a tune gets relative pitches right. Businesspeople have good intuition

about relative risks, at least in industries they are used to, but not about absolute

risk or required rates of return. Therefore, they set a companywide cost of capital

as a benchmark. This is not the right hurdle rate for everything the company does,

but adjustments can be made for more or less risky ventures.

The analogy is borrowed from S. C. Myers and L. S. Borucki, “Discounted Cash Flow Estimates of

the Cost of Equity Capital—A Case Study,” Financial Markets, Institutions, and Investments 3 (August

1994), p. 18.

Brealey−Meyers:

Principles of Corporate

Finance, Seventh Edition

II. Risk 9. Capital Budgeting and

Risk

Companies, 2003

Suppose that you are considering an across-the-board expansion by your firm. Such

an investment would have about the same degree of risk as the existing business.

Therefore you should discount the projected flows at the company cost of capital.

Companies generally start by estimating the return that investors require from

the company’s common stock. In Chapter 8 we used the capital asset pricing model

to do this. This states

An obvious way to measure the beta (␤) of a stock is to look at how its price has re-

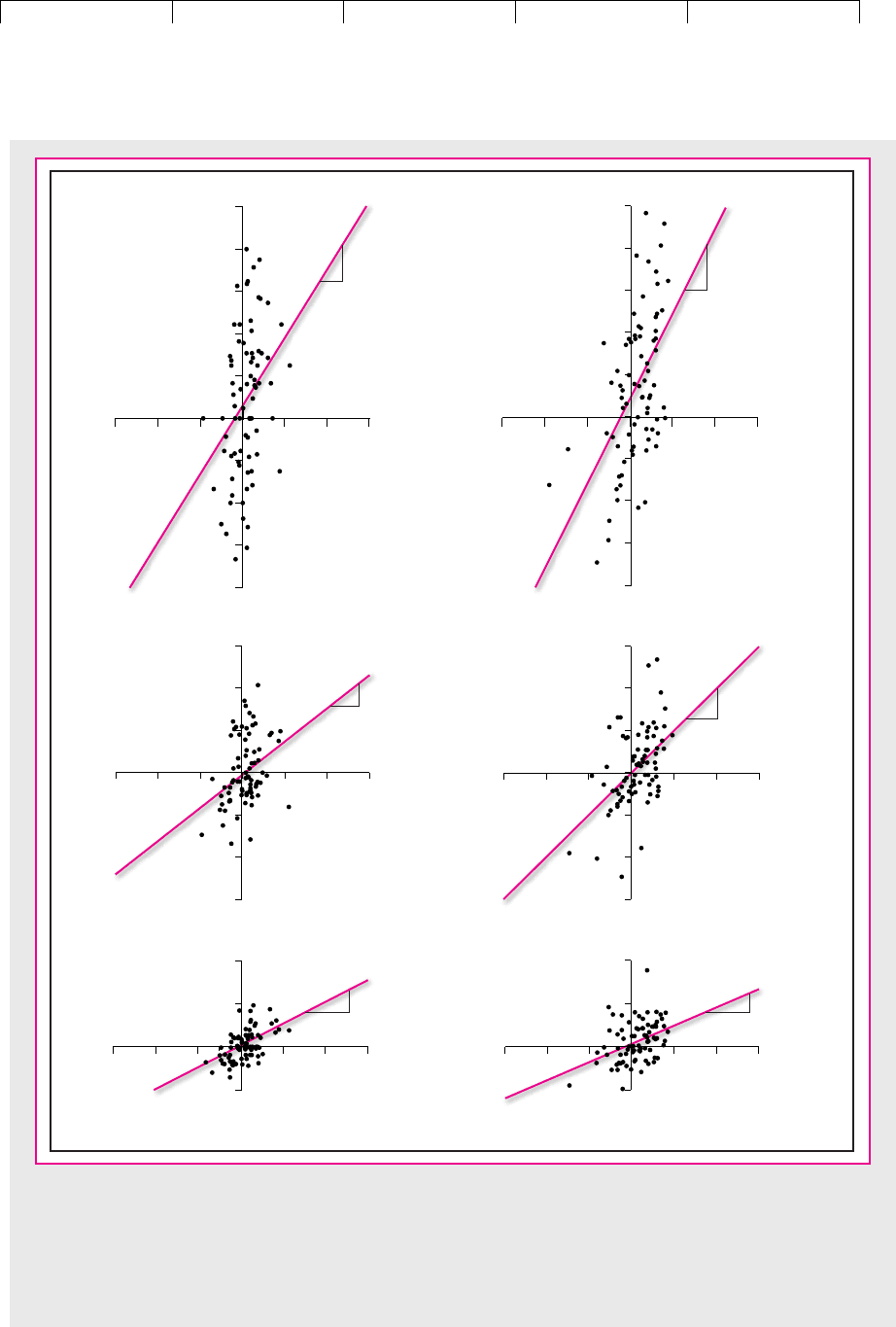
sponded in the past to market movements. For example, look at the three left-hand

scatter diagrams in Figure 9.2. In the top-left diagram we have calculated monthly re-

turns from Dell Computer stock in the period after it went public in 1988, and we have

plotted these returns against the market returns for the same month. The second dia-

gram on the left shows a similar plot for the returns on General Motors stock, and the

third shows a plot for Exxon Mobil. In each case we have fitted a line through the

points. The slope of this line is an estimate of beta.

It tells us how much on average

the stock price changed for each additional 1 percent change in the market index.

The right-hand diagrams show similar plots for the same three stocks during the

subsequent period, February 1995 to July 2001. Although the slopes varied from the

first period to the second, there is little doubt that Exxon Mobil’s beta is much less

than Dell’s or that GM’s beta falls somewhere between the two. If you had used the

past beta of each stock to predict its future beta, you wouldn’t have been too far off.

Only a small portion of each stock’s total risk comes from movements in the mar-

ket. The rest is unique risk, which shows up in the scatter of points around the fitted

lines in Figure 9.2. R-squared (R

) measures the proportion of the total variance in the

stock’s returns that can be explained by market movements. For example, from 1995

to 2001, the R

for GM was .25. In other words, a quarter of GM’s risk was market risk

and three-quarters was unique risk. The variance of the returns on GM stock was 964.

So we could say that the variance in stock returns that was due to the market was

and the variance of unique returns was

The estimates of beta shown in Figure 9.2 are just that. They are based on the

stocks’ returns in 78 particular months. The noise in the returns can obscure the true

beta. Therefore, statisticians calculate the standard error of the estimated beta to show

the extent of possible mismeasurement. Then they set up a confidence interval of the

estimated value plus or minus two standard errors. For example, the standard error

of GM’s estimated beta in the most recent period is .20. Thus the confidence interval

for GM’s beta is 1.00 plus or minus 2 ⫻ .20. If you state that the true beta for GM is

between .60 and 1.40, you have a 95 percent chance of being right. Notice that we can

be more confident of our estimate of Exxon Mobil’s beta and less confident of Dell’s.

Usually you will have more information (and thus more confidence) than this

simple calculation suggests. For example, you know that Exxon Mobil’s estimated

.75 ⫻ 964 ⫽ 723..25 ⫻ 964 ⫽ 241,

Expected stock return ⫽ r

⫹␤1r

⫺ r

224 PART II Risk

9.2 MEASURING THE COST OF EQUITY

Notice that you must regress the returns on the stock on the market returns. You would get a very sim-

ilar estimate if you simply used the percentage changes in the stock price and the market index. But

sometimes analysts make the mistake of regressing the stock price level on the level of the index and ob-

tain nonsense results.

This is an annual figure; we annualized the monthly variance by multiplying by 12 (see footnote 17 in

Chapter 7). The standard deviation was percent.2964 ⫽ 31.0

Brealey−Meyers:

Principles of Corporate

Finance, Seventh Edition

II. Risk 9. Capital Budgeting and

Risk

Companies, 2003

-10-20-30 0 10 20 30

-30

-40

-20

-10

-30 -20 -10 0 10 20 30

-40

-30

-20

-10

-30 -20 -10 0 10 20 30

-30

-20

-10

-30 -20 -10 0 10 20 30

-30

-20

-10

-30 -20 -10 0 10 20 30

-10

-30 -20 -10 0 10 20 30

-10

Dell Computer

return %

August 1988–

January 1995

β = 1.62

(.52)

= .11

Dell Computer

return %

February 1995–

July 2001

Market return, % Market return, %

β = 2.02

(.38)

= .27

August 1988–

January 1995

Market return, % Market return, %

General Motors

return %

β = .8

(.24)

= .13

February 1995–

July 2001

General Motors

return %

β = 1.00

(.20)

= .25

February 1995–

July 2001

Exxon Mobil

return %

August 1988–

January 1995

Market return, % Market return, %

β = .52

(.10)

= .28

Exxon Mobil

return %

β = .42

(.11)

= .16

FIGURE 9.2

We have used past returns to estimate the betas of three stocks for the periods August 1988 to January 1995 (left-

hand diagrams) and February 1995 to July 2001 (right-hand diagrams). Beta is the slope of the fitted line. Notice that

in both periods Dell had the highest beta and Exxon Mobil the lowest. Standard errors are in parentheses below the

betas. The standard error shows the range of possible error in the beta estimate. We also report the proportion of

total risk that is due to market movements (R

225

Brealey−Meyers:

Principles of Corporate

Finance, Seventh Edition

II. Risk 9. Capital Budgeting and

Risk

Companies, 2003

beta was well below 1 in the previous period, while Dell’s estimated beta was well

above 1. Nevertheless, there is always a large margin for error when estimating the

beta for individual stocks.

Fortunately, the estimation errors tend to cancel out when you estimate betas of

portfolios.

That is why financial managers often turn to industry betas. For example,

Table 9.1 shows estimates of beta and the standard errors of these estimates for the

common stocks of four large railroad companies. Most of the standard errors are

above .2, large enough to preclude a precise estimate of any particular utility’s beta.

However, the table also shows the estimated beta for a portfolio of all four railroad

stocks. Notice that the estimated industry beta is more reliable. This shows up in

the lower standard error.

The Expected Return on Union Pacific Corporation’s Common Stock

Suppose that in mid-2001 you had been asked to estimate the company cost of cap-

ital of Union Pacific Corporation. Table 9.1 provides two clues about the true beta

of Union Pacific’s stock: the direct estimate of .40 and the average estimate for the

industry of .50. We will use the industry average of .50.

In mid-2001 the risk-free rate of interest r

was about 3.5 percent. Therefore, if

you had used 8 percent for the risk premium on the market, you would have con-

cluded that the expected return on Union Pacific’s stock was about 7.5 percent:

226 PART II Risk

Standard

␤

equity

Error

Burlington Northern & Santa Fe .64 .20

CSX Transportation .46 .24

Norfolk Southern .52 .26

Union Pacific Corp. .40 .21

Industry portfolio .50 .17

TABLE 9.1

Estimated betas and costs of (equity) capital for a

sample of large railroad companies and for a

portfolio of these companies. The precision of the

portfolio beta is much better than that of the

betas of the individual companies—note the lower

standard error for the portfolio.

If the observations are independent, the standard error of the estimated mean beta declines in propor-

tion to the square root of the number of stocks in the portfolio.

Comparing the beta of Union Pacific with those of the other railroads would be misleading if Union

Pacific had a materially higher or lower debt ratio. Fortunately, its debt ratio was about average for the

sample in Table 9.1.

This is really a discount rate for near-term cash flows, since it rests on a risk-free rate measured by the

yield on Treasury bills with maturities less than one year. Is this, you may ask, the right discount rate

for cash flows from an asset with, say, a 10- or 20-year expected life?

Well, now that you mention it, possibly not. In 2001 longer-term Treasury bonds yielded about

5.8 percent, that is, about 2.3 percent above the Treasury bill rate.

The risk-free rate could be defined as a long-term Treasury bond yield. If you do this, however,

you should subtract the risk premium of Treasury bonds over bills, which we gave as 1.8 percent in

Table 7.1. This gives a rough-and-ready estimate of the expected yield on short-term Treasury bills

over the life of the bond:

The expected average future Treasury bill rate should be used in the CAPM if a discount rate is

needed for an extended stream of cash flows. In 2001 this “long-term r

” was a bit higher than the

Treasury bill rate.

⫽ .058 ⫺ .019 ⫽ .039, or 3.9%

Expected average T-bill rate ⫽ T-bond yield ⫺ premium of bonds over bills