Boyd T.J.M., Sanderson J.J. The Physics of Plasmas

Подождите немного. Документ загружается.

11.2 WKBJ model of inhomogeneous plasma 427

where

(z) =

− ω

(z)

(11.2)

For a homogeneous plasma the electric ﬁeld satisfying (11.1) has the form

E(z, t) = A exp[i(φ(z) − ωt)] where A is constant and φ(z) = kz. For the

inhomogeneous case in which the plasma density is a slowly varying function of

z, we keep this form for the ﬁeld and set out to ﬁnd a representation for the phase

φ(z), sometimes referred to as the eikonal. Then, dropping the time dependence,

= iAφ



iφ

iAφ



− A(φ



)

iφ

in which φ



= dφ/dz, φ



= d

φ/dz

. Substituting in (11.1) gives

iφ



− (φ



)

+ k

(z) = 0 (11.3)

For plasmas in which the density varies on a sufﬁciently long scale length the φ



term may be taken to be small compared with k

(z) giving



=±k(z)φ



=±k



(z)

Then from (11.3)



(z) =



(z) ± ik



(z)



1/2

±k(z) +



(z)

2k(z)

φ(z) ±



k(z)dz + i ln

k(z)

The integration constant may be set to zero by an appropriate choice for the lower

limit of the integral, but is left unspeciﬁed for the time being since it does not affect

the argument. Consequently the spatial dependence of the electric ﬁeld takes the

form

E(z) =

1/2

(z)

exp



±i



k(z)dz



(11.4)

This WKBJ solution corresponds to right (+) and left (−) travelling waves. The

wave forms in (11.4) resemble plane waves with phases expressed as an integral

over the region of propagation but with an amplitude that is only weakly spatially

varying. A useful rule of thumb for the validity of WKBJ solutions follows from

the requirement that φ



in (11.3) be much less than k

, leading to the condition



 k (11.5)

428 Aspects of inhomogeneous plasmas

Clearly (11.5) is violated when k → 0 (cut-off) or when dk/dz →∞(resonance).

When the WKBJ method fails we generally have to resort to numerical solution

of the parent differential equation. For consistency we need to check how well the

solutions satisfy the Maxwell equations. In the ﬁrst place we ﬁnd that the wave

magnetic ﬁeld decreases as cut-off is approached in contrast to the swelling of the

electric ﬁeld. Consistency provides a more precise validity condition as to what is

meant by ‘slowly varying’. Unless this condition is satisﬁed one solution generates

some of the other so that the two waves in (11.4) are no longer independent and

reﬂection occurs.

Now consider an electromagnetic wave propagating from a source at z = 0 into

a plasma of increasing density. The electric ﬁeld of this wave may be represented

(z) =

1/2

(z)

exp





k(z)dz



and that of the reﬂected wave as

(z) =

1/2

(z)

exp



−i



k(z)dz



where R denotes the reﬂection coefﬁcient for wave amplitude. If we now let z →

, where z = z

is a cut-off point, and equate the two ﬁelds in this region, turning

a blind eye to WKBJ breakdown, it follows that

R = exp





k(z)dz



(11.6)

The integral in (11.6) is known as the phase integral since it measures the change

in phase of the wave from source to the cut-off and back. Not surprisingly (11.6)

is not a correct representation of the reﬂection coefﬁcient. We shall ﬁnd in the

following section that it differs from the true value by a factor i.

The WKBJ method is a mathematical representation of ray-tracing and its ex-

tension to three dimensions, known as the eikonal or ray-tracing approximation,

is widely used (see Weinberg (1962)). The amplitude of the wave is taken as

exp[iφ(r, t)], where φ(r, t) satisﬁes ∇φ = k(r, t) and ∂φ/∂t =−ω(r, t), and

the direction of energy ﬂow is given by v

= ∂ω/∂k. If we denote the dispersion

relation by

(

ω, k, r, t

)

= 0 (11.7)

we can express ω = ω

(

k, r, t

)

. The ray trajectories are then determined by the set

of equations (see Exercise 11.3):

=−

∂ D/∂k

∂ D/∂ω

=−

∂ D/∂r

∂ D/∂ω

dω

=−

∂ D/∂t

∂ D/∂ω

(11.8)

11.2 WKBJ model of inhomogeneous plasma 429

Fig. 11.1. The function k

(z) showing regions of validity of the WKBJ aapproximation.

Starting from a source at the plasma boundary that injects a given spectrum of

wavenumbers, (11.8) can be integrated to ﬁnd the ray characteristics. Numerical

ray-tracing codes ﬁnd wide application across many areas of plasma physics.

11.2.1 Behaviour near a cut-off

The next task is to see how to deal with behaviour near a cut-off. At a cut-off (or

C-point) the incident wave is reﬂected and k

(z) changes sign from positive to

negative. Figure 11.1 shows a cut-off at z = z

in a region z

≤ z ≤ z

over which

WKBJ solutions fail. For z ≤ z

the solutions correspond to incident and reﬂected

waves as we saw in the previous section. Beyond z

, WKBJ solutions are again

valid but now correspond to evanescent and amplifying waves. In the evanescent

wave both electric and magnetic ﬁelds decay spatially and there is no energy ﬂux

beyond the C-point. Clearly an amplifying solution is non-physical in the absence

of a source of energy. Across the region z

≤ z ≤ z

, k

(z) may be represented as

(z) =−





(z − z

) + O(z − z

)

430 Aspects of inhomogeneous plasmas

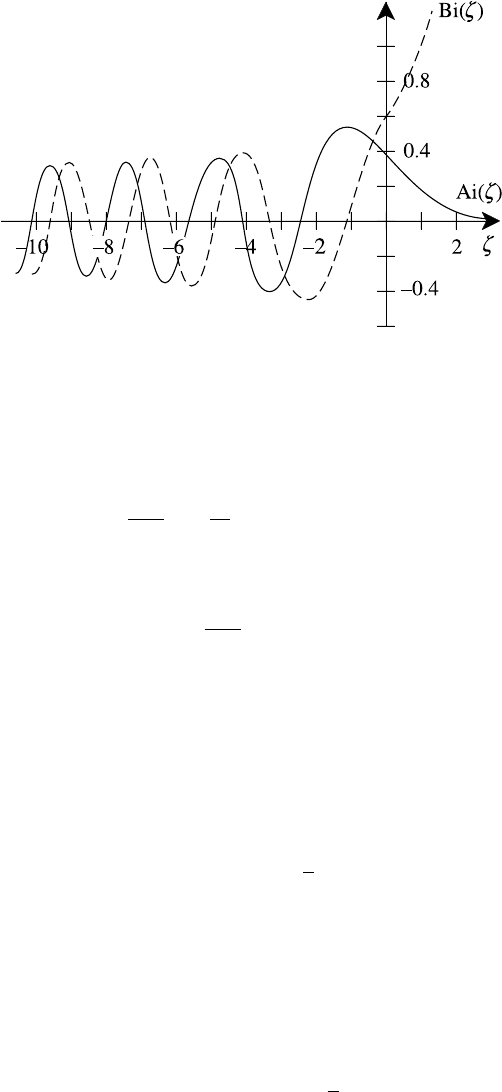
Fig. 11.2. Ai(ζ ) and Bi(ζ ) (dashed curve).

where k

is a constant, not to be confused with k

) = 0, and (k

) is real and

positive. Thus across this region (11.1) becomes

−





(z − z

)E = 0

which can be cast as Stokes’ equation

dζ

= ζ E (11.9)

by making use of the transformation ζ =





1/3

(z − z

). Stokes’ equation has

no singularities for ﬁnite ζ . Its solution is therefore ﬁnite and single-valued and is

expressed in terms of Airy functions Ai(ζ ),Bi(ζ ) represented in Fig 11.2.

Solutions to Stokes’ equation have to be considered over the complex ζ -plane.

We can readily write down WKBJ solutions to Stokes’ equation; disregarding

constants

E = ζ

−1/4

exp



3/2



(11.10)

A linear combination of these solutions is a good representation across the ranges

indicated in Fig. 11.1. However, since these are multiply valued functions, the

solution to Stokes’ equation, being single-valued, cannot be represented by the

same combination for all ζ . For example, for real positive ζ (arg ζ = 0), the WKBJ

approximation to Ai(ζ ) is given by

Ai(ζ ) = Aζ

−1/4

exp



−

3/2



(11.11)

11.2 WKBJ model of inhomogeneous plasma 431

On the other hand, if we keep |ζ | constant and set arg ζ = π, this representation

clearly fails. For a correct general representation we need both terms in (11.10),

i.e.

Aζ

−1/4

exp



−

3/2



+ Bζ

−1/4

exp



3/2



with the proviso that the constants A and B take on different values as ζ moves

in the complex plane. The need for this was ﬁrst recognized by Stokes and

is known as the Stokes phenomenon. The exponents involved are real for arg

ζ = 0, 2π/3, 4π/3. For large |ζ | one contribution is exponentially large (the

dominant term), the other exponentially small (subdominant). A fuller discussion

of the Stokes’ solutions has been given by Budden (1966).

We can now return to reconsider the reﬂection coefﬁcient discussed earlier. This

requires a solution of the wave equation across the entire range. The argument is

quite general but for sake of reference we consider it in the context of a light wave

incident from z = 0 on a plasma containing a region across which the density

varies linearly with z. Over that part of the range beyond z

, the solution contains

only the subdominant term so that over the region z

≤ z ≤ z

the solution is

determined by Ai(ζ ). This solution has to ﬁt on to the WKBJ solutions below the

cut-off, i.e.

−1/2



exp





k(z)dz



+ R exp



−i



k(z)dz



Multiplying this by the constant exp(−i



k(z)dz) and recasting in terms of ζ we

ﬁnd the solution valid over the range (z

, z

) is proportional to

−1/4



exp



−

3/2



+ R exp



−2i



k(z)dz



exp



3/2



This form must be identical to the approximation for Ai(ζ ) for arg ζ = π so that

R = i exp





k(z)dz



(11.12)

which differs from the result (11.6) by a phase factor π/2.

In general two different representations of a function can match only over some

limited range of z before phase divergence becomes serious. Implicit in the match-

ing is the assumption that there is a region of overlap across which both the eikonal

solution and the asymptotic Airy solution are each valid representations. Matching

will clearly not be possible if k

(z) is signiﬁcantly non-linear before valid WKBJ

solutions are reached.

432 Aspects of inhomogeneous plasmas

11.2.2 Plasma reﬂectometry

The reﬂection of a wave at cut-off lends itself to a versatile and widely used di-

agnostic, plasma reﬂectometry. Simply detecting a reﬂected wave is evidence that

at some point in the proﬁle the density is supercritical. The question of interest is

precisely where reﬂection occurs. Finding the cut-off point requires a measurement

of the relative phases of the incident and reﬂected waves. The electron density

proﬁle may be unfolded by sweeping the frequency of the incident wave. The tech-

nique has been widely applied to tokamak plasmas and has the advantage of both

good spatial (≤ 1 cm) and temporal (≤ 5 µs) resolution. Reﬂectometry has certain

features in common with interferometry, but whereas interferometry builds up an

electron density proﬁle from measurements along different chords (of a cylindrical

plasma), reﬂectometry constructs the same proﬁle from phase measurements at

different frequencies. One of the difﬁculties inherent in reﬂectometry arises from

the effect of density perturbations on propagation of the incident wave, though

techniques have been developed to get round this difﬁculty. Different types of

reﬂectometer are used in plasma diagnostics. In the simplest, a single frequency is

used, with the frequency swept linearly across a broadband range. Strong (MHD)

ﬂuctuations in the plasma present problems should this sweep be too slow.

For simplicity we consider O-wave propagation and ignore relativistic correc-

tions. We saw from the previous section that the phase shift of the reﬂected wave

is given by

φ =



(ω

− ω

(z))

1/2

dz −

This phase shift may be expressed as a time delay τ = dφ/dω and if τ is measured

for frequencies within the range of interest, one may then determine the position

of the cut-off from an Abel inversion:

(ω) = z



τ(ω



)

(ω

− ω

2

)

1/2

dω



(11.13)

From this relation, knowing the phase delay for frequencies less than ω, the posi-

tion of the cut-off may be found. Since measurements cannot be carried out from

ω = 0, an extrapolation is needed from some level to the plasma edge, assuming

some density proﬁle.

While measurements using a single frequency spectrum are widely used in prac-

tice, this approach suffers from the limitations imposed by the length of the interval

needed for the diagnostic to map the density proﬁle. There is an intrinsic limit to the

time resolution of the reﬂectometer since the proﬁle is unfolded step by step. Thus

the measurement of the density proﬁle needs to be completed within an interval

short enough that signiﬁcant changes in plasma parameters do not occur. Density

ﬂuctuations present between the boundary of the plasma and the cut-off affect wave

11.3 Behaviour near a resonance 433

propagation and are the source of inaccuracies in constructing the density proﬁle.

Fluctuations with short scale length give rise to destructive interference; however,

unless the plasma is in a highly turbulent state it is usually possible to unfold a

density proﬁle, albeit at the cost of reduced resolution.

11.3 Behaviour near a resonance

Resonances are less straightforward to deal with than cut-offs since the essential

physics governing the resonance has to be incorporated to obtain physically mean-

ingful results. Whereas waves undergo reﬂection at cut-offs, resonances are char-

acterized by absorption of the wave energy by the plasma. As the wave approaches

a resonance, n = ck/ω →∞so that the wave is refracted toward the resonant

surface and reaches it at normal incidence. Since condition (11.5) is increasingly

well satisﬁed, no reﬂection occurs. What happens to the energy carried by the

wave to the resonance (or R-point)? In the strict cold plasma limit, this energy

could only be stored in the form of currents, resulting in the non-physical limit

of increasingly large rf power density. However in real plasmas, ﬁnite temperature

ensures that the refractive index of the plasma remains ﬁnite even at a resonance. In

warm plasmas, the consequent damping, however small, means that some heating

takes place. Even in the cold plasma limit where there is no dissipation, a small

amount of damping, ν, has to be introduced into the analysis in order to move

the singularity at the resonance (ω

(z) − ω)

−1

off the real axis and so determine

how the solution is to be continued around the singularity. In physical terms, if

one examines the transport of wave energy to the resonance, the time required to

approach the R-point varies as ν

−1

. In hot plasmas Coulomb collisions near the

resonance are ineffective as an agent for energy dissipation so that an alternative

means is needed. This alternative is provided by linear mode conversion which

converts the incident wave to a warm plasma wave. Thus as well as C-points and

R-points we now identify X -points, in the neighbourhood of which linear mode

conversion takes place.

An issue of importance in discussing resonances in inhomogeneous plasmas

is the question of their accessibility. In the radiofrequency heating of laboratory

plasmas a wave is launched from an antenna conﬁguration outside the plasma and

propagates to a region within the plasma where the resonance is sited. Formally,

the resonance is accessible if k

(z)>0 at all points on the density proﬁle below

the resonant density. However, if a C-point is present en route to the R-point then

reﬂection there will prevent the wave from reaching the resonance. One important

exception to this appears in cases where the cut-off and resonance stand back-to-

back. Between cut-off and resonance the wave is evanescent (k

(z)<0). If the

separation between the points is not too great some fraction of the incident wave

434 Aspects of inhomogeneous plasmas

energy can tunnel through the evanescent region beyond the C-point to reach the

resonance. Such a conjunction of C-andR- points occurs not only in radio wave

propagation in the ionosphere but in the resonant absorption of laser light by target

plasmas.

The ﬁrst analysis of the physics of a cut-off and resonance back-to-back was

carried out by Budden (1966) who used a wave equation with the form

+ k



1 +



E = 0 (11.14)

This provides the simplest representation for a back-to-back cut-off and resonance,

with the resonance at z = 0 and the cut-off at z =−z

. With suitable substitutions

(11.14) may be cast in standard form with solutions expressed in terms of conﬂuent

hypergeometric functions. Asymptotic solutions for large positive z may be con-

nected to those for z large and negative, with a small amount of damping introduced

to resolve the singularity present. A wave travelling to the right encounters the

cut-off ﬁrst and is in part reﬂected while some fraction tunnels through beyond

the C-point. Budden found (amplitude) reﬂection and tunnelling (transmission)

coefﬁcients

|R|=1 − e

−2η

|T |=e

−η

(11.15)

where η =

πk

. A wave travelling to the left meets the resonance ﬁrst as shown

in Fig. 11.3. The tunnelling coefﬁcient is symmetric in the two cases but there is

no reﬂection at the resonance for incidence from the right so that

|R|=0 |T |=e

−η

(11.16)

Physically, the parameter η provides a measure of the number of vacuum wave-

lengths that ﬁt between the cut-off and resonance. For right-propagating waves,

η  1 implies that most of the incident ﬂux penetrates to the resonance. For η  1,

tunnelling is ineffective for right-propagating waves resulting in almost total reﬂec-

tion. It is clear from both expressions (11.15) and (11.16) that |R|

+|T |

< 1, i.e.

energy is not conserved.

The ingredient missing from Budden’s equation is mode conversion which is

important in regions of the plasma over which two modes that in general satisfy

distinct dispersion relations, and thus propagate as independent modes, no longer

do so. Over such regions, modes can interact strongly with one another. In mode

conversion a wave incident from one side of the region in question will emerge

from the other side as a linear combination of two modes. Mode conversion is

important in practice in the absorption of electromagnetic energy by a plasma,

leading to heating.

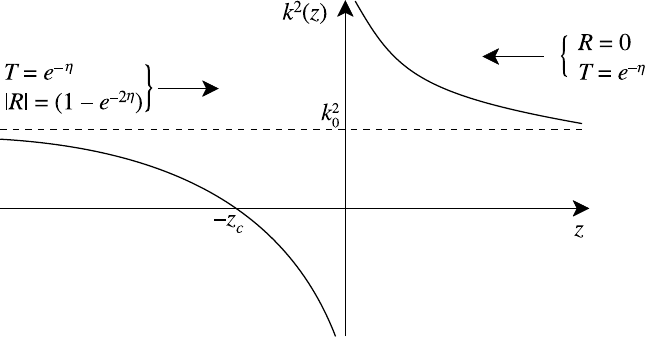
11.4 Linear mode conversion 435

Fig. 11.3. Behaviour of k

(z) in the neighbourhood of a cut-off resonance pair.

11.4 Linear mode conversion

Mode conversion operates over regions where otherwise distinct modes have a

common wavelength. Outside such a region, coupling between modes is weak and

one would expect WKBJ solutions to provide a satisfactory representation of the

propagation characteristics of each mode. However, within this region the WKBJ

approximation breaks down and an alternative formulation is needed to charac-

terize wave propagation. One approach extrapolates the homogeneous dispersion

relation, D(ω, k) = 0, to represent local wave characteristics by means of a new

relation D(ω, k, z) = 0. A differential equation may then be constructed from this

algebraic equation by introducing a mapping k →−id/dz, an operation that is not

in general unique.

If one considers a one-dimensional model of two modes subject to mode conver-

sion and allows for propagation in either direction then the governing dispersion

relation is fourth-order in k so that mapping in this way produces a fourth-order

differential equation. One such equation constructed by Erokhin (1969)

(iv)

+ λ



+ (λ

z + γ)y = 0 (11.17)

has been widely used as a paradigm mode conversion equation. Since the coef-

ﬁcients are linear in z, solutions may be found in the form of a contour integral

y(z) =



F(k) exp(−ikz) dz. The asymptotic properties of a solution having this

form are found by the method of steepest descents. The saddle points are found

and the contribution to the asymptotic solution from a saddle point gives a WKBJ

solution. The asymptotic solutions correspond to superpositions of the WKBJ

436 Aspects of inhomogeneous plasmas

solutions for the separate waves. However this procedure provides a solution across

the region where no WKBJ solution is possible. The contour C is chosen to thread

the saddle points giving the required behaviour (see Swanson (1985, 1989)). Dis-

carding y

(iv)

in (11.17) reproduces Budden’s equation. The important difference

here is that the energy missing from Budden’s equation is now mode-converted to

the slow wave branch.

Quite apart from the non-uniqueness of the operation k →−id/dz, the anal-

ysis involved in such an approach is both complex and cumbersome to apply. A

simpler alternative is based on the idea that is central to mode coupling, namely

that just two modes are involved and the propagation of each is governed by

distinct differential equations except for a limited region across which the modes

(and hence the equations) are coupled. This local coupling provides the means by

which power can ﬂow from one mode to the other in the coupling region. One can

show for example how a system of differential equations may be transformed to

separate out a second-order system in the neighbourhood of a mode conversion

point (see Heading (1961)). Away from the mode conversion point the solutions to

this equation represent a superposition of the two modes involved. This approach

has since been used and adapted by Fuchs, Ko and Bers (1981) and by Cairns and

Lashmore-Davies (1983); see Cairns (1991). In fact the method was ﬁrst devised

in 1932, independently by Landau and by Zener, in treating the pseudo-crossing

of potential energy curves in a quantum mechanical description of slow adiabatic

atomic collisions; see Landau and Lifshitz (1958). Indeed the energy transmission

coefﬁcient found from the mode-coupling analysis in this section ((11.21) below)

is readily recovered from the Landau–Zener transition probability after an appro-

priate transcription of variables.

Coupling involving two modes is illustrated in Fig. 11.4 which shows the cross-

ing of the individual dispersion curves for the uncoupled modes k = k

(z),

k = k

(z). In the neighbourhood of this curve-crossing, the dispersion relation

is assumed to take the form

[k − k

(z)][k − k

(z)] = χ (11.18)

in which the coupling term χ is signiﬁcant only in the neighbourhood of the cross-

ing point z = z

of the (uncoupled) dispersion curves. The next step is to convert

this local dispersion relation to a second-order differential equation by identifying

k with −i d/dz. To get round the difﬁculty introduced by the non-uniqueness of

this procedure Cairns and Lashmore-Davies proposed that uniqueness be ensured

by a choice compatible with energy conservation. For modes with positive group

velocities (as in Fig. 11.4) they introduced mode amplitudes φ

and φ

normalized