Boyd T.J.M., Sanderson J.J. The Physics of Plasmas

Подождите немного. Документ загружается.

11.7 Effects in bounded plasmas 457

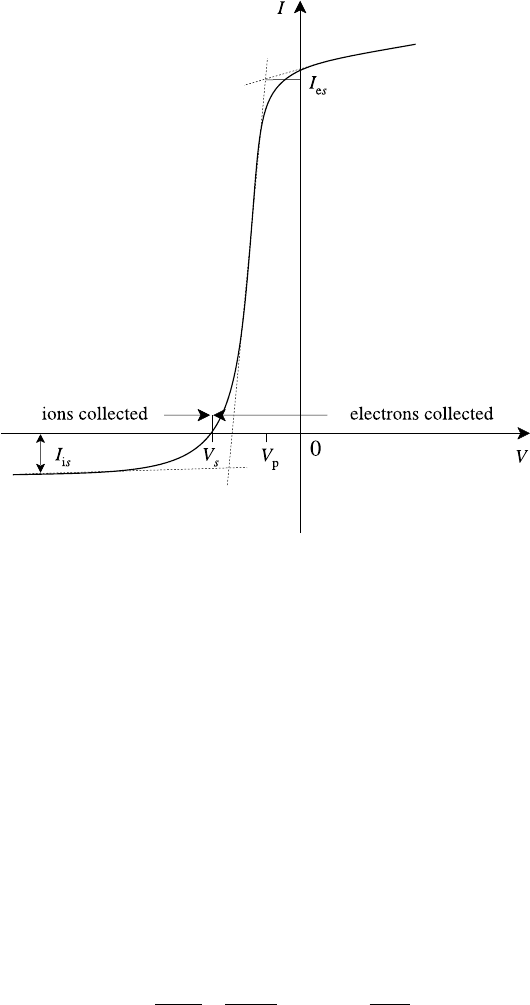
Fig. 11.15. Langmuir probe characteristic showing the variation of the probe current with

probe potential.

Thus once the electron temperature is known, the Bohm saturation current deter-

mines the plasma density.

As V becomes less negative with respect to the plasma, energetic electrons from

the tail of the distribution are collected by the probe until, at the ﬂoating potential

, electron and ion currents cancel one another. A further increase in V leads to

a steep rise in electron current which eventually saturates at space potential, the

potential of the plasma V

 0.

Consider the Langmuir characteristic in the region V

< V < V

in which

electron current is drawn. Over this region the electron sheath shields the probe

from electrons other than those with sufﬁcient energy to overcome the potential

barrier. The electron current to the probe is then the random current, reduced by

the Boltzmann factor, i.e.



πm



1/2

exp





(11.58)

so that the total current drawn to the probe is

I = I

+ I

(11.59)

458 Aspects of inhomogeneous plasmas

From the slope of the characteristic we can determine the electron temperature.

From (11.58), (11.59)

If we use the region of the characteristic where the slope is greatest we may

disregard dI

/dV so that

(I − I

(11.60)

This can be determined directly from the characteristic by measuring its slope as

shown in Fig. 11.15.

The Langmuir probe technique is a versatile diagnostic in plasmas of moderate

density and temperature. If the density is high enough for electron and ion mean

free paths to become comparable to probe dimensions the model is no longer valid.

Exercises

11.1 Consider a light wave propagating along Oz in a plasma of increasing

density n(z). By appealing to the conservation of energy ﬂux show that

|E(z)|=E

/ε

1/4

where E

denotes the amplitude of the electric ﬁeld in

vacuo and ε is the plasma dielectric function. Compare this result with the

WKBJ ﬁeld amplitude. How is |B(z)| related to B

11.2 Show that the validity condition for WKBJ solutions to the wave equation

may be expressed as







−



 1

11.3 Express ∂k/∂t =−∇ω as

∂ω

∂r

+∇k ·

∂ω

∂k

∂t

= 0

and by considering the dispersion relation as a function of k, r and t, i.e.

(

k, r, t

)

, k, r, t

)

= 0 so that

∂ D

∂k

∂ D

∂ω

∂k

= 0

∂ D

∂r

∂ D

∂ω

∂r

= 0

∂ D

∂t

∂ D

∂ω

∂t

= 0

establish the set of equations (11.8) that determine ray trajectories.

11.4 Verify the steps leading to the reﬂection coefﬁcient R given by (11.12).

Note that the representation for Ai(ζ ) valid for arg ζ = π is

Ai(ζ ) ∼

−1/2

−1/4



exp



−

3/2



+ i exp



3/2



Exercises 459

11.5 Consider an electromagnetic wave propagating along the density gradient

in a plasma in which the electron density varies as n(z) = n

(z/L). From

the analysis outlined in Section 11.2.1, the electric ﬁeld is determined by

the Airy function Ai(ζ ) shown in Fig. 11.2.

By matching this electric ﬁeld to the vacuum electric ﬁeld at z = 0,

show that

E(ζ ) =

√

2π(k

1/6

iφ

Ai(ζ )

where E

is the amplitude of the vacuum ﬁeld and φ is a phase factor. The

Airy function Ai(ζ) has a maximum value 0.535 at ζ =−1 corresponding

to z = L

1 − (k

−2/3

. Show that



max



 1.8(k

1/3

which provides an estimate of the swelling of the electric ﬁeld as the wave

approaches the cut-off.

Estimate the swelling of the WKBJ electric ﬁeld by representing ε

min

as the value of ε averaged over a half wavelength near cut-off. Show that

min

 (π c/ωL)

2/3

. Hence show that

max

 1.4(k

1/3

In contrast to the WKBJ approximation in which k

= 0 it is possible to

deﬁne a local incident wavenumber k

from the Airy solution. Show that

 0.6k

2/3

−1/3

11.6 Consider a light wave incident obliquely on a plasma slab. Take Oyz to be

the plane of incidence and the angle of incidence θ = cos

−1

(

k ·

z). In the

case of oblique incidence we have to distinguish between two polarization

states, S and P, in which E is respectively perpendicular to, and coplanar

with, the plane of incidence. For an S-polarized wave the wave electric

ﬁeld gives rise to electron oscillations in the x-direction, along which the

density is uniform. The electric ﬁeld of a P-polarized wave on the other

hand causes electrons to oscillate across regions of non-uniform density;

in this case the wave is no longer purely electromagnetic.

For S-polarized light show that the results of Exercise 11.5 carry over

after making allowance for the fact that reﬂection now takes place at

ε(z) = sin

θ, i.e. reﬂection takes place at a density below critical, where

= n

cos

θ.

By contrast, a P-polarized wave at its cut-off has its electric ﬁeld aligned

along the density gradient and, provided the separation between cut-off and

resonance is not too large, some fraction of the incident electric ﬁeld can

tunnel through to the resonance and excite a Langmuir wave. Interactions

between resonant electrons and the Langmuir wave excited in this way

460 Aspects of inhomogeneous plasmas

result in resonant absorption of the incident radiation. To estimate the

electric ﬁeld E

along the direction of the density gradient near the crit-

ical density, ﬁrst express E

(z) = [B(z) sin θ ]/[cε(z)] = E

(z)/ε(z).To

determine the resonant ﬁeld one has to ﬁnd B(L). A simple way of doing

this uses a physical argument given by Kruer (1988), which represents

B(L) by its value at the turning point, B(L cos

θ) multiplied by a factor

to allow for the exponential decay from cut-off to resonance. Show that

B(L cos

θ) 

0.9E



ωL



1/6

where E

is the intensity of the electric ﬁeld in vacuo. The decay of

the ﬁeld beyond cut-off may be represented by a factor e

−β

where

β = (1/c)



L cos



− ω

cos



1/2

dz. Evaluate β and show that

(L)  0.9E



ωL



1/6

sin θ exp



−2ωL sin



Deﬁning τ = (ωL/c)

1/3

sin θ, show that this may be written

(L) =

(2πωL/c)

1/2

φ(τ)

where the shape function φ(τ)  2.3τ exp(−2τ

/3).

Note that E

(L) → 0asτ → 0, i.e. θ → 0. Similarly for large

τ , E

(L) → 0 corresponding to the cut-off occurring at too low a

density for the wave to tunnel effectively to the critical density surface.

Between these limits there is an optimum angle of incidence given by

(ωL/c)

1/3

sin θ  0.8. The shape function found from this heuristic argu-

ment provides a good approximation to the numerical solution of the wave

equation (see Denisov (1957)).

11.7 Following linear conversion to Langmuir waves the electrostatic ﬁeld en-

ergy is resonantly transferred to electrons by means of Landau damping.

Representing damping phenomenologically we may write

ε(z) =



1 −



iν





Show that the energy ﬂux that is resonantly absorbed, I

= f

,is

determined by



(z)

|ε(z)|

Exercises 461

where z

, z

denote C- and R-points. Show that this reduces to (Kruer

(1988))





= f





so that I

. Simulations of absorption of P-polarized light con-

ﬁrm that resonance absorption of about 40% takes place.

11.8 The frequency and wavenumber matching conditions for forward and

backward Raman scattering are ω

= ω

+ ω

, k

= k

± k

, where the

plus sign denotes SRFS and the minus, SRBS. Show that the wavenumber

matching conditions may be written



1 −



1/2

= k



1 −



1/2

In the limit k

 1 show that k

 (ω

/c)(1 − 2ω

/ω

)

1/2

so that



1 −



1/2





1 − 2



1/2

From this it is clear that SRS matching conditions can only be satisﬁed

for densities up to quarter-critical, n

/4. At this density k

 0 so that

∼ k

= (

√

3ω

/2c). For densities much below n

/4, show that



∓



1 −



Thus for SRBS at very low densities k

= 2k

, while for SRFS, k

= ω

/c.

11.9 Carry out a ﬁrst-order perturbation analysis on the electron ﬂuid equations

to obtain the SRS coupled equations (11.23), (11.24) for a homogeneous

plasma. Fourier analyse these equations to ﬁnd the SRS dispersion relation

(11.25).

Show that the maximum homogeneous Raman growth rate is given by

(11.26). Allowing for damping of the Langmuir wave and the scattered

light wave conﬁrm that the Raman growth rate is now given by (11.29).

11.10 Recover (11.33) and (11.34), the second-order SRS equations for an inho-

mogeneous plasma, from (11.32).

Show that the WKBJ equations for an inhomogeneous plasma are given

by (11.36) and (11.37). By combining these equations establish (11.38).

Show that the convective gain is given by (11.45). In the case of a linear

density proﬁle with scale length L conﬁrm that the SRBS threshold is

determined by (11.47).

462 Aspects of inhomogeneous plasmas

11.11 A plasma is contained in the right half-space x > 0, i.e. a density step from

n = 0ton = n

appears at x = 0. Consider a surface wave in which the

electric ﬁeld is electrostatic with the potential

φ(x, y, t) = φ

(x) exp i(ky − ωt) + c.c.

Show that φ

(x) = φ

exp(−|k|x) where φ

denotes the potential at the

boundary. Applying boundary conditions at x = 0 show that the dispersion

relation for the electrostatic surface wave is ω

= ω

/2.

Show that in the case of electromagnetic surface waves in the short

wavelength limit, the surface wave dispersion relation becomes

− ω

− 2ω

11.12 Tonks and Langmuir (1929) found that in a cylindrical discharge plasma

the principal resonance appeared at ω

√

2. Subsequently Romell (1951)

observed in addition a series of weaker resonances, later studied by Dattner

(1957, 1963) and others and known as Tonks–Dattner resonances.

Consider a slab of plasma of uniform density n

and thickness 2L,

unbounded in the other two dimensions. Show that the set of resonant

frequencies ω

is given by

= ω



1 + 3

(

m + 1/2

)



where λ

is the Debye length. This result predicts a spacing



ω

/ω



which is an order of magnitude too small. To ﬁx this one has to take

account of plasma inhomogeneity.

Starting from the ﬂuid model of a warm plasma (6.86)–(6.88) with a

perturbation scheme deﬁned by

n(x, t) = n

(x) + n

(x)e

−iωt

E(x, t) = E

(x) + E

(x)e

−iωt

v(x, t) = 0 + v

(x)e

−iωt

p(x, t ) = p

(x) + p

(x)e

−iωt



show that, to ﬁrst order, the perturbation in electron density is determined

+ k

(x)n

3mV



(

)

+ E



If we denote the scale length of the inhomogeneity by L show that the

Exercises 463

terms on the right-hand side are typically (1/kL) times those on the left so

that

3λ



− ω

(x)



 0 (E11.1)

where ω

, λ

denote the electron plasma frequency and the Debye length

at the centre of the plasma. This model shows that electron plasma waves

can now propagate in the region between the boundary and a point x

which the plasma density becomes critical, i.e. n(x

) = n

. Since we have

already assumed that the density scale length is much greater than the

electron plasma wavelength we may use a WKBJ approximation to ﬁnd

the eigenvalues



k(x)dx =



m +



π m = 0, 1, 2,... (E11.2)

Useful as this electrostatic model is, it too fails when it comes to inter-

preting the spectra observed experimentally. Work by Parker, Nickel and

Gould (1964), in which neither the electrostatic assumption nor the WKBJ

approximation was made, determined the spectrum of resonances numeri-

cally for a cylindrical plasma column and compared these results with their

measured spectra. Refer to their paper for the satisfactory agreement they

found between theory and experiment.

11.13 By integrating (11.55) twice across the sheath and taking dφ/dξ = 0at

the edge show that the sheath is typically a few Debye lengths thick.

The classical theory of plasmas

12.1 Introduction

In this ﬁnal chapter an attempt is made to sketch the classical mathematical struc-

ture underlying the various theoretical models which have been used throughout

the book. The knowledge of where a particular model ﬁts within the overall picture

helps us both to understand the relationship to other models and to appreciate its

limitations. Of course, we have touched upon these relationships and limitations

already so the task remaining is to construct the framework of classical plasma

theory and show how it all ﬁts together.

Since collisional kinetic theory is the most comprehensive of the models that we

have discussed we could begin with it as the foundation of the structure we wish to

build. Indeed, we shall demonstrate its pivotal position. This would, however, be

less than satisfactory for two reasons. The ﬁrst and basic objection is that, so far,

we have merely assumed a physically appropriate model for collisions. We have

not carried out a mathematical derivation of the collision term. In fact, enormous

effort has gone into this task though we shall present only a brief resum

e. In

doing so, we shall show how the separation of the effects of the Coulomb force

into a macroscopic component (self-consistent ﬁeld) and a microscopic component

(collisions) appears quite naturally in the mathematical derivation of the collisional

kinetic equation. This is the second reason for starting at a more fundamental level

than the collisional kinetic equation itself.

To lighten the burden of the mathematical analysis we have, wherever con-

venient, restricted calculations to a one-component (electron) plasma. The ions,

however, are not ignored but treated as a uniform background of positive charge.

Electrons interact with the ions but this appears as a ‘ﬁeld’ rather than an inter-

particle interaction. Extensions of important formulae to multi-component plasmas

are given at appropriate places in the text.

464

12.2 Dynamics of a many-body system 465

12.2 Dynamics of a many-body system

Going back to ﬁrst principles and assuming, for simplicity, that the motion of the

N electrons in a plasma obeys the laws of classical mechanics, we may write down

N Newtonian equations

(t) = F

(t)(i = 1, 2,...,N ) (12.1)

in which m is the electron mass, R

(t) is the position of the ıth electron at time t

and F

(t)is the force it experiences at that position and time. Formal solutions of

these N equations are

(t) =

(0) +





) dt



(t) = R

(0) +

(0)t +











) dt



(i = 1, 2,...,N ) (12.2)

In principle, this completely determines the motion of the plasma. In practice,

it is impossible to carry out the integrations in (12.2) since F

is, in general, a

function of the positions and velocities of all the plasma particles; the N vector

equations (12.1) are coupled in a very complicated way. Moreover, even if the

forces were sufﬁciently simple that one could do the integrations, there would never

be sufﬁcient information to supply the required 2N initial conditions R

(0),

(0)

(i = 1, 2,...,N ).

Turning now to a description of the plasma in terms of distribution functions, the

exact N -particle distribution function f

, v

,...,r

, v

, t) is given by

, v

,...,r

, v

, t) =

i=1

δ[r

− R

(t)]δ[v

−

(t)] (12.3)

since (12.2) formally prescribes the position and velocity of each particle. Taking

the partial derivative of f

with respect to t and using (12.3) we get

∂ f

∂t



i=1



∂ f

∂R

∂ f

∂



=−



i=1



∂ f

∂r

∂ f

∂v



466 The classical theory of plasmas

since ∂δ(x − y)/∂y =−∂δ(x − y)∂ x. However, f

is zero unless

= v

and

from (12.1)

= F

/m so this may be written

∂ f

∂t



i=1



∂ f

∂r

∂ f

∂v



= 0 (12.4)

So far the description of plasma motion by (12.4) is equivalent to that given by

(12.1). However, the lack of information concerning initial conditions leads us to

seek a statistical interpretation of the distribution function. Since the initial con-

ditions are unknown, probability considerations may be applied to them. Instead

of the distribution function at t = 0 being zero everywhere except at a single

point in the 6N -dimensional phase space (r

, v

,...,r

, v

) it will be given by

a smoother function f

, v

,...,r

, v

, t = 0) which is an ensemble average

over the many possible (but unknown) initial starting points in phase space. As

time evolves, each initial point traces out a locus in phase space, determined by the

dynamics of the system, thus prescribing f

(t), which we deﬁne by the statement

that f

, v

,...,r

, v

, t)

i=1

is the probability of ﬁnding the system

within the volume element

i=1

about the point (r

, v

,...,r

, v

) at time

t. Replacing the exact distribution function f

by f

in (12.4) then gives the

Liouville equation

= 0 (12.5)

where the Liouville operator

≡

∂

∂t



i=1



∂

∂r

∂

∂v



(12.6)

The Liouville equation is the starting point for a statistical description of a many-

body system and, for a classical system, is usually written

∂ f

∂t

+ [ f

, H ] = 0 (12.7)

where H is the Hamiltonian of the system and the Poisson bracket

[ f

, H ] ≡



i=1



∂ f

∂q

∂ H

∂p

−

∂ f

∂p

∂ H

∂q



, p

being the generalized coordinates and momenta. For the non-relativistic

plasma that we consider

H =



i=1

+ V (q

, q

,...,q

, t) (12.8)