Boyd T.J.M., Sanderson J.J. The Physics of Plasmas

Подождите немного. Документ загружается.

12.4 The Landau equation 477

Fig. 12.1. Time variation of |r

− (v

− v

)(t − t



)|; φ

≈ 0 unless both r

and |r

−

− v

)(t − t



)| lie within a Debye sphere.

Then

g =





G(r

, r



, r



, t, t



)

∂φ



)

∂r





∂ f (r



, v

, t



)

∂v

f (r



, v

, t



) −

∂ f (r



, v

, t



)

∂v

f (r



, v

, t



)







∂φ

(|r

− (v

− v

)(t − t



)|)

∂r



∂ f (r

− v

(t − t



), v

, t



)

∂v

f (r

− v

(t − t



), v

, t



)

−

∂ f (r

− v

(t − t



), v

, t



)

∂v

f (r

− v

(t − t



), v

, t



)



(12.45)

Substitution of this expression for g in (12.24) (with φ replaced by φ

) does not

immediately yield a tractable kinetic equation because of the arguments of f in

the collision term. Indeed, one might say that it does not yet amount to a kinetic

equation at all because g is not expressed as a functional (as opposed to a function)

of f . However, Bogolyubov’s hypothesis leads to a number of simpliﬁcations so

that g does become a functional of f making (12.23) a kinetic equation.

Note ﬁrst that since the arguments of the shielded potentials in (12.24) and

(12.45) are r

and |r

− (v

− v

)(t − t



)| and φ

(r) ≈ 0 for r  λ

it follows

that the time interval (t −t



)  λ

/|v

−v

|∼ω

−1

; this is illustrated in Fig. 12.1.

Next, since we assume that f does not vary signiﬁcantly on this time scale (ω

−1

)

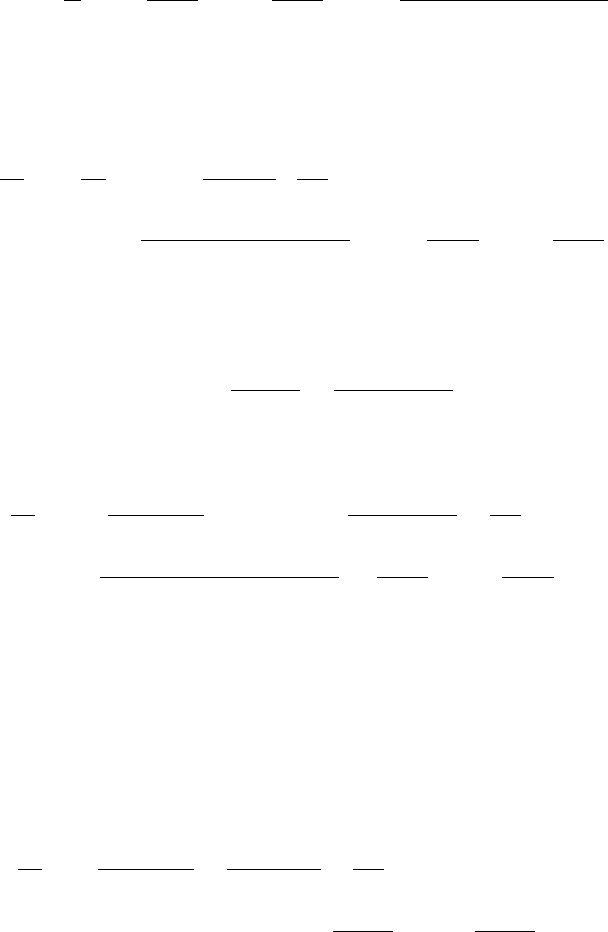
478 The classical theory of plasmas

nor over distances of order λ

, the arguments of f in (12.45) may be reduced to

, v

, t) and (r

, v

, t) in which r

≈ r

. Letting τ = t − t



we may now rewrite

(12.45) as

g(1, 2) =



f (2)

∂ f (1)

∂v

− f (1)

∂ f (2)

∂v





∞

∂φ

(|r

− (v

− v

)τ |)

∂r

dτ

(12.46)

where we have taken the limit t →∞in the integral, which is allowed because,

as already observed, the integrand vanishes for τ  ω

−1

. This expression for g is

now a functional of f and substitution in (12.24) gives



∂ f

∂t





∂φ

)

∂r

∂

∂v



∞

dτ

∂φ

(|r

− (v

− v

)τ |)

∂r



f (2)

∂ f (1)

∂v

− f (1)

∂ f (2)

∂v



(12.47)

Writing φ

(r) in terms of its Fourier transform

(r) =

(2π)



dk exp(ik · r)

+ k

where k

≡ λ

−1

, (12.47) becomes



∂ f

∂t



=−

(2π)



dk dl

exp(ik ·r

)

+ k

)

k ·

∂

∂v



∞

dτ

exp{il ·[r

− (v

− v

)τ ]}

+ k

)

l ·



∂ f (1)

∂v

f (2) −

∂ f (2)

∂v

f (1)



(12.48)

To simplify this expression we integrate over r

space ﬁrst. In doing this we use

a similar approximation to that for the time integration in (12.45) and assume

f varies on a length scale much greater than λ

; since the integrand in (12.48)

contains φ(r

) it vanishes exponentially for r

 λ

so that we may replace r

by r

in f (2). The integration over r

then involves exp[−i(k + l) · r

] only and

gives (2π)

δ(k+l). The integration over l space is then trivial and (12.48) becomes



∂ f

∂t



(2π)



+ k

)

k ·

∂

∂v



∞

dτ exp[ik ·(v

− v

)τ ]k ·



∂ f (v

)

∂v

f (v

) −

∂ f (v

)

∂v

f (v

)



(12.49)

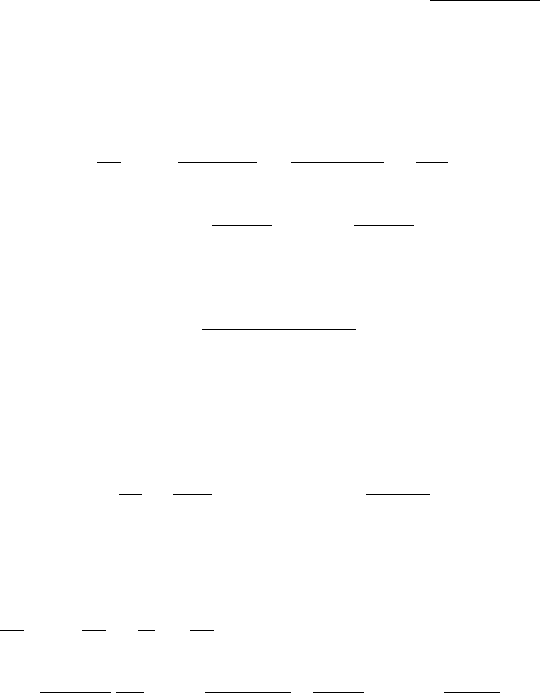
12.4 The Landau equation 479

The integration over τ is given by the Plemelj formula



∞

dτ exp[ik ·(v

− v

)τ ] = πδ[k ·(v

− v

)] − iP

k · (v

− v

)

(12.50)

where P stands for the principal part. However, the second term in (12.50) gives

no contribution to (12.49), since it makes the integrand odd in k (its contribution

must be zero since it is imaginary). Hence



∂ f

∂t



8π



+ k

)

k ·

∂

∂v

δ[k · (v

− v

)]

k ·



∂ f (v

)

∂v

f (v

) −

∂ f (v

)

∂v

f (v

)



(12.51)

Deﬁning g = (v

− v

), this leaves an integration over k space of the form



k · Aδ(k · g)k · B

+ k

)

dk (12.52)

which diverges at large k. This is a direct result of the weak coupling approximation

which clearly breaks down as r

→ 0, in fact for r

 e

/4πε

T . We cut off

the integration therefore at k = 4πε

T/e

and ﬁnd for (12.52)

π A



−



ln  = π A

∂

∂v

ln  (12.53)

where  = 4πnλ

and only terms in ln  have been retained.

Thus, using (12.21), the kinetic equation may ﬁnally be written

∂ f

∂t

+ v ·

∂ f

∂r

−

E ·

∂ f

∂v

ln 

8πε

∂

∂v





∂

|v − v



∂v



∂ f (v)

∂v

f (v



) −

∂ f (v



)

∂v



f (v)



(12.54)

where E is the self-consistent ﬁeld given by (12.22). This form of the collision

integral for a plasma was ﬁrst derived by Landau using an intuitive model for

collisions, so (12.54) is known as the Landau kinetic equation.

At this point it is of interest to consider the relationship of the Landau equation

to the Balescu–Lenard equation (12.28). A comparison of (12.28) with (12.51)

shows that the dielectric function (k, k · v

), has simply been replaced by the

term (1 +(k

/k)

), which is the static shielding factor introduced by replacing the

Coulomb potential φ by the shielded potential φ

. In fact the main effect of the

dielectric function is to produce shielding, but in the Balescu–Lenard equation it

appears as a dynamic effect involving the interaction of particles and Fourier wave

480 The classical theory of plasmas

components through the resonant integral in (12.30). Furthermore, it can be shown,

as for example in Nicolson (1983), that to the order of keeping only terms in ln 

the Balescu–Lenard collision integral reduces to the Landau collision integral.

The generalization of the Landau collision integral to more than one species of

particle is given by (8.36). Since the latter equation was derived from the Fokker–

Planck equation this establishes an important link and justiﬁes the applicability of

the Fokker–Planck model to a plasma.

12.5 Moment equations

In Section 7.2 we showed through Jeans’ theorem the formal equivalence of the

collisionless (Vlasov) kinetic theory and particle orbit theory. We turn now to the

relationship between collisional (Landau) kinetic theory and the MHD equations

discussed in Chapters 3–5. There is no simple theorem establishing this relation-

ship for there is not, even in a formal sense, an exact equivalence. The procedure

from microscopic kinetic description to macroscopic ﬂuid description has rather

more in common with the derivation of the kinetic equation from the Liouville

equation. The reduction in detail of description, in this case the removal of depen-

dence on the velocity coordinate v, gives rise to an inﬁnite chain of equations – the

moment equations. The derivation of the moment equations is the ﬁrst of the three

basic steps that lead to the MHD equations. The second and most formidable is the

truncation and closure of the moment equations. This is where physical approxima-

tion enters and equivalence disappears; it is the subject of classical transport theory

discussed in Section 12.6. The ﬁnal step is the derivation of the MHD equations

from the transport equations and the further physical approximations necessary for

this are examined in Section 12.7.

We begin with deﬁnitions of ﬂuid variables in which we introduce the label α

(= i, e, for ions and electrons, respectively), to denote particle species. On scalars

α appears as a subscript but on vectors and tensors, for which we frequently need

to denote components by roman subscripts ( j, k, l etc.), it is more convenient to

write α as a superscript. Since f

(r, v, t)dr dv is the probability at time t of ﬁnding

particles of type α within a small volume element dr dv about the point (r, v)

the integral of this over all velocity space is the probability of ﬁnding particles,

irrespective of velocity, within a volume dr about r. Hence, the (number) density,

(r, t) is deﬁned by

(r, t) =



dv f

(r, v, t) (12.55)

Similarly, the ﬂow velocity u

(r, t) is the mean velocity of all particles of type α

12.5 Moment equations 481

in the volume dr about r at time t and so is given by

(r, t) =



v f

(r, v, t)dv



(r, v, t)dv

(r, t)



v f

(r, v, t)dv (12.56)

Other ﬂuid variables like pressure, temperature and heat ﬂux are deﬁned in terms

of the random or thermal velocities of the particles

= v − u

(12.57)

Whilst the mean value of c

is clearly zero, the mean values of higher powers of

its components are non-zero in general and, for example, are related to the thermal

momentum ﬂux and thermal energy ﬂux and thereby to the pressure and heat ﬂux.

Thus, we deﬁne the elements of the pressure tensor p

(r, t) by

(r, t) = m



(r, v, t)dv (12.58)

and the heat ﬂux tensor q

ijk

(r, t) by

ijk

(r, t) = m



(r, v, t)dv (12.59)

It is convenient to separate p

into two tensors by

= p

+ 

(12.60)

where



= m





−



dv (12.61)

is by deﬁnition a traceless tensor and



dv (12.62)

is, for an isotropic plasma, the scalar pressure.

It is also useful to deﬁne a kinetic temperature T

(r, t) by extrapolating the well-

known result that for an ideal gas in equilibrium the thermal energy associated

with each degree of freedom of the gas is

. Since Boltzmann’s constant k

is always associated with T

we shall, in this chapter, absorb it into the deﬁnition

of T

(which is thereby measured in energy units instead of degrees). Thus, with

three degrees of freedom for each of the n

particles we have

(r, t)



(r, v, t)dv =

(12.63)

482 The classical theory of plasmas

Finally, the heat ﬂux vector q

(r, t) is the ﬂux of thermal energy relative to the

ﬂow velocity and so is given by

(r, t) =



(r, v, t)dv (12.64)

It then follows from (12.59) that

(r, t) =

ijj

(r, t) (12.65)

These velocity integrals by which the ﬂuid variables are deﬁned are called ‘mo-

ment integrals’ of f

. The order of a moment integral is given by the highest power

of the components of v occurring in the integrand. Thus, the density is a zero-order

moment, the ﬂow velocity is a ﬁrst-order moment, the pressure and temperature

are second-order moments and the heat ﬂux is a third-order moment.

We now generate evolution equations for these macroscopic variables by taking

appropriate moments of the kinetic equation

∂ f

∂t

+ v ·

∂ f

∂r

(E + v × B) ·

∂ f

∂v



∂ f

∂t



(12.66)

Since r, v and t are independent variables it is clear from (12.55) that when we

integrate (12.66) over velocity space (i.e. take the zero-order moment) the ﬁrst

term in the new equation is ∂n

/∂t so that this may be regarded as an equation for

the time evolution of n

(r, t). It is also evident from (12.56) that the second term

gives rise to ∇ · (n

), that is, the evolution equation for the zero-order moment

contains a term involving the ﬁrst-order moment u

. We obtain an evolution

equation for u

by taking the ﬁrst-order moment of (12.66), that is we multiply by

v and then integrate over velocity space. Now the leading term is ∂(n

)/∂t but

the second term again gives rise to a higher moment,



vv f

dv, which by (12.58)

is somehow related to the pressure tensor as well as to n

and u

. Clearly, this

drawing down of higher moments persists no matter how many moments of the ki-

netic equation we take. We have removed a variable (v) of inﬁnite dimension but, in

doing so, have generated an inﬁnite chain of moment equations. Such mathematical

transformations do not reduce the basic complexity of the description. To achieve

this we need approximations based on physical assumptions. Up to this point we

have merely outlined a scheme for replacing one equation in seven-dimensional

space (r, v, t) by an inﬁnite set of equations in four-dimensional space (r, t) and

there is, thus far, an exact equivalence between these descriptions. For the present,

we shall not worry about how the real simpliﬁcation is to be achieved but will go

ahead and generate the ﬁrst few equations in the chain.

12.5 Moment equations 483

It is useful to obtain a general moment equation by multiplying (12.66) by ψ(v),

where ψ(v) is any polynomial function of the components of v, and integrating

over velocity space. Deﬁning

ψ=



ψ(v) f



(r, t)



ψ(v) f

(r, v, t) dv (12.67)

we get

∂

∂t

ψ) +

∂

∂r

· (n

vψ)

−



∂ψ

∂v



−



(v × B) ·

∂ψ

∂v







∂ f

∂t



(12.68)

where we have used integration by parts to obtain the third and fourth terms

assuming that f

→ 0 faster than any inverse power of |v| as |v|→∞, i.e.

lim

|v|→∞

(ψ f

) = 0.

The following useful relationships are easily veriﬁed using (12.57)–(12.65) and

(12.67):

v

=(c

+ u

)(c

+ u

)

=c

+u



+ u

(12.69)

v

=(c

+ u

)(c

+ u

)



=c

+2c

u

+ u

c

+u

2

+ u

(12.70)

The collisional conservation relations are of fundamental importance in the

derivation of the ﬂuid equations. We have





∂ f

∂t



= 0 (α = i, e) (12.71)





dvv



∂ f

∂t



= 0 (12.72)





dv v



∂ f

∂t



= 0 (12.73)

Thus, when ψ(v) = 1 the collision term makes no contribution to the moment

equation (12.68) for either ions or electrons. Also, when ψ(v) = m

v or

the ion and electron collision terms are equal in magnitude but opposite in sign.

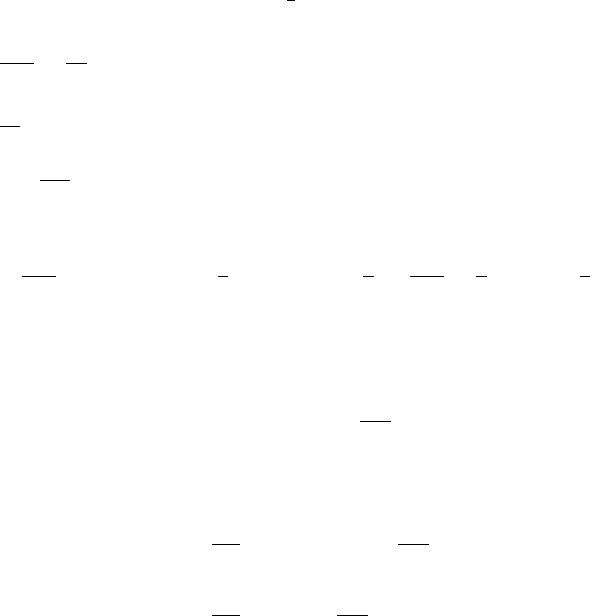
484 The classical theory of plasmas

In turn we now set ψ(v) = 1, m

in (12.68) to get

∂n

∂t

∂

∂r

· (n

) = 0 (12.74)

∂

∂t

) +

∂

∂r

+ n

+ 

) − e

+ (u

× B)

) = R

(12.75)

∂T

∂t

+ n

· ∇T

∇ · u



∂u

∂r

∇ · q

(12.76)

where

= m



dvv



∂ f

∂t



(12.77)

is the rate of transfer of momentum to species α from the other species and



dv |v −u



∂ f

∂t





dv v



∂ f

∂t



− u

· R

(12.78)

is the rate of transfer of thermal energy. In deriving (12.78), (12.71) and (12.77)

have been used. It is easily seen that consequences of the conservation relations

(12.72) and (12.73) are

=−R

(12.79)

and

=−Q

− (u

− u

) · R

(12.80)

The momentum equation (12.75) can be simpliﬁed using the continuity equa-

tion (12.74) but, with subsequent manipulations in mind, we choose not to do

this. However, the energy equation (12.76) has been reduced using both (12.74)

and (12.75). Because of the special role of collisions in classical (and neoclassical)

transport theory the three moment equations (12.74)–(12.76) are particularly im-

portant and although, for an adequate account of transport theory, it is necessary to

generate further moments these will not be displayed.

12.5 Moment equations 485

12.5.1 One-ﬂuid variables

The ﬂuid variables we have deﬁned and the moment equations that have been

derived for their evolution amount to a two-ﬂuid description of the plasma. But

the MHD equations, our ultimate goal, are cast in terms of a single ﬂuid. The

ﬁnal exercise in this section, therefore, is to introduce one-ﬂuid hydrodynamical

and electrodynamical variables and make a (partial) transformation of the moment

equations. At this stage a complete transformation to a one-ﬂuid description would

be inappropriate. The reason for this is that the exchange of thermal energy between

ions and electrons is a rather inefﬁcient process and can be as slow as the hydrody-

namical changes taking place in the plasma. In transport theory the separation of

fast (collisional) and slow (hydrodynamic) time scales is the key to the truncation

procedure. It is essential, therefore, to retain separate evolution equations for ion

and electron temperatures. The one-ﬂuid variables are the plasma mass density

ρ(r, t) =



(r, t) (12.81)

the charge density

q(r, t) =



(r, t) (12.82)

the centre of mass (or plasma ﬂow) velocity u(r, t) deﬁned by

ρ(r, t)u(r, t) =



(r, t)u

(r, t) (12.83)

and the current density

j(r, t) =



(r, t)u

(r, t) (12.84)

With the aid of this set of equations and its inverse

Zeρ − m

e(m

+ Zm

)

≈

Zρ

−

≈

Zρ

eρ − m

e(m

+ Zm

)

≈

Zeρu − m

Zeρ − m

Zeρu − m

Zeρ − m

≈ u −

Zeρ

eρu + m

eρ + m

≈ u = u











(12.85)

we can transform the two-ﬂuid moment equations (12.74) and (12.75) to their

equivalent one-ﬂuid moment equations for ρ,q, u and j. The small electron to

ion mass ratio allows us to simplify the new equations for u and j by taking the

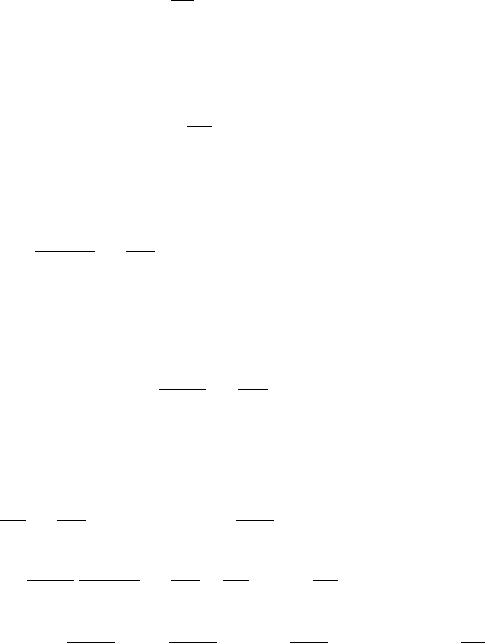
486 The classical theory of plasmas

→ 0 limit. The ﬁrst set of approximations (third column) in (12.85) corre-

sponds to this limit. The second set of approximations (ﬁnal column) is obtained

in the limit |q|Zeρ/m

and allows a further simpliﬁcation of these equations.

This approximation is a consequence of the assumption of quasi-neutrality since

what we mean by this is that the charge imbalance should be a very small fraction

of the electronic or ionic charge, that is

|q|en

≈ Zen

≈ Zeρ/m

(12.86)

Multiplying the ion and electron versions of (12.74) by their respective masses

and adding gives, on using (12.81) and (12.83),

∂ρ

∂t

+ ∇ · (ρu) = 0 (12.87)

which is the one-ﬂuid continuity equation. Multiplying by the respective charges

and adding gives, on using (12.82) and (12.84), the equation of charge conservation

∂q

∂t

+ ∇ · j = 0 (12.88)

Both (12.87) and(12.88) are, of course, exact.

Next we add the ion and electron versions of (12.75) to obtain

∂(ρu

)

∂t

∂

∂r

(ρu

+ Pδ

+ 

)

− qE

− (j × B)

= 0 (12.89)

where the total scalar pressure

P ≈

ZρT

ρT

≈ n

+ n

(12.90)

and terms of order (Zm

) and (m

q/Zeρ) have been neglected. Likewise, mul-

tiplying (12.75) by e

and adding we obtain in the same approximation

∂ j

∂t

∂

∂r



+ j

−

Zeρ



−

∂(ρT

)

∂r

∂

∂r





−





−



u −

Zeρ



× B



=−

(12.91)

This equation is the generalized Ohm’s law since it relates the current to the elec-

tromagnetic ﬁelds and, under conditions yet to be discussed, reduces to the simple

Ohm’s law (3.35).