Boyd T.J.M., Sanderson J.J. The Physics of Plasmas
Подождите немного. Документ загружается.

12.6 Classical transport theory 497
and also find a heat flux driven by the electric field
q
e
= α
T
e
E (12.130)
which is related to the Peltier effect in thermocouples.
Fourier’s law for electrons
q
e
=−κ
e
∇T
e
(12.131)
is recovered when
ˆ
E = 0, i.e. when the electric force on the electrons balances
the electron pressure gradient, en
e
E =−∇ p
e
. In this case there is still an electric
current produced by the electron temperature gradient
j =−α
∇T
e
This is the thermoelectric effect.
It is obvious from (12.121) that for B = 0, X
α
= 0 and so all of the transport
coefficients are proportional to a collision time,
L
∝ τ
α
(12.132)
The implication of this is that collisions impede transport parallel to the magnetic
field, as one would expect since it is only collisions that interrupt the flow of mat-
ter, momentum and energy in response to the thermodynamic forces. In this case
the dependence on density and temperature can be simply expressed because the
dimensionless functions
˜
L
are functions of Z only. From (12.121) and(12.122),
using Z
e
=−1, Z
i
= Z , and writing
A =
6
√
2π
3/2
ε
2
0
ln
(12.133)
we find
σ
=
AT
3/2
e
e
2
m
1/2
e
˜σ
(Z )
Z
(12.134)
α
=
0
5
2
AT
3/2
e
e
3
m
1/2
e
˜α
(Z )
Z
(12.135)
κ
α
=
5AT
5/2
α
2e
4
m
1/2
α
˜κ
α
(Z )
|ZZ
3
α
|
(12.136)
µ
α
=
Am
1/2
α
T
5/2
α
e
4
˜µ
α
(Z )
|ZZ
3
α
|
(12.137)
Ignoring the weak density and temperature dependence contained in A through
ln we see that all coefficients increase with temperature, with the thermal con-
ductivities and viscosities showing a particularly strong dependence, and all coeffi-
cients are independent of density. This latter feature is typical of the weak coupling

498 The classical theory of plasmas
approximation applied to the Landau kinetic equation and is true for the transport
coefficients of a dilute neutral gas as well.
The electrical conductivity and thermoelectric coefficient are, of course, deter-
mined by the electrons because of their much smaller mass and this has already
been taken into account by ignoring terms of order m
e
/m
i
. But now from (12.136)
and (12.137) we can compare electron and ion thermal conductivities and viscosi-
ties. We see that
κ
i
κ
e
=
m
e
m
i
1/2
T
i
T
e
5/2
1
Z
3
˜κ
i
(Z )
˜κ
e
(Z )
(12.138)
and
µ
i
µ
e
=
m
i
m
e
1/2
T
i
T
e
5/2
1
Z
3
˜µ
i
(Z )
˜µ
e
(Z )
(12.139)
in which the mass ratio dependence indicates the predominance of electron thermal
conductivity and ion viscosity. Thus, parallel to the magnetic field, energy is mainly
transported by the electrons and momentum by the ions though it should be noted
that for high Z or T
e
T
i
electron viscosity could become significant.
All of this discussion of the parallel transport coefficients holds good when
B = 0. This is because the equations for the parallel moments decouple from
those for the perpendicular moments and are independent of the magnetic field.
In other words, if we were to plot the variation with X
α
=
α
τ
α
of the dimen-
sionless transport coefficients, the parallel coefficients
˜
L
(Z ), being functions of
Z only, would be horizontal straight lines, as in Fig. 12.2. This is not the case
for the perpendicular coefficients, of course. From (12.123) and (12.124) we see
that some of these, ˜σ
⊥
, ˜α
⊥
, ˜κ
α
⊥
, ˜µ
α
2
and ˜µ
α
4
, start at X
α
= 0 with values equal to
the corresponding parallel coefficient while the others are all zero at X
α
= 0.
Representing all the initially non-zero set by the label
˜
L
⊥
and the others by
˜
L
∧
we
find that for fixed Z ,
˜
L
⊥
decreases in magnitude as X
α
increases, while
˜
L
∧
first
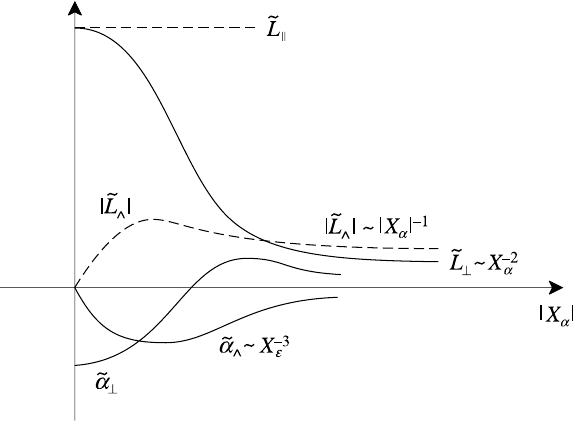
increases in magnitude and then decreases. This is shown schematically in Fig.
12.2 where the decrease in
˜
L
⊥
is presented as monotonic. This is true for all except
˜α
⊥
which is actually negative at X
α
= 0 and first decreases in magnitude, passes
through zero, and then asymptotically approaches zero as X
α
→∞. Although the
figure is only schematic it should be noted that all the
˜
L
⊥
∼ X
−2
α
as X
α
→∞
whereas, with the single exception of ˜α
∧
, all the |
˜
L
∧
|∼|X
α
|
−1
;˜α
∧
∼ X
−3
e
decays
fastest of all.
The asymptotic behaviour of the perpendicular transport coefficients
˜
L
⊥
∼
1
(
α
τ
α
)
2
(12.140)
means that classical transport across magnetic field lines decreases with the square
12.6 Classical transport theory 499
Fig. 12.2. Schematic illustration of variation of transport coefficients with |X
α
|.
of the magnetic field. Unfortunately, this turns out not to be true of toroidal confine-
ment devices where other factors, notably the geometry of the field, come into play.
Transport is neoclassical rather than classical and the perpendicular coefficients
vary more like B
−1
.
The dependence on collision time is also very interesting and shows a sharp
contrast with the parallel coefficients. From (12.121) and (12.140) we see that the
perpendicular coefficients vary like τ
−1
α
as X
α
→∞, that is they increase with the
collision frequency ν
α
= τ
−1
α
. Thus, while collisions impede parallel transport they
increase perpendicular transport. The reason for this is easily understood and was
discussed in some detail in Section 8.2.1. In a strong magnetic field particles are
restricted to Larmor orbits in the plane perpendicular to B so transport is impeded
by the field. But collisions disrupt this ordered motion and allow particles to slip
across field lines thereby enhancing perpendicular transport. Note that the contrast-
ing dependence on collision frequency of parallel and perpendicular coefficients
means that in the presence of a strong field, as the collision frequency is increased,
effective transport of matter, momentum and energy is transferred progressively
from the parallel to the perpendicular direction.
The dependence on density and temperature shows a marked difference as well.
From (12.121) and (12.140) it is easily seen that all perpendicular coefficients in-
crease asymptotically with the square of density and decrease with temperature; σ
⊥
and α
⊥
are proportional to T
−3/2
e
while κ
α
⊥
and µ
α
2
decrease like T
−1/2
α
. Yet another
500 The classical theory of plasmas
striking result arises from a comparison of ion and electron thermal conductivities.
We find
κ
i
⊥
κ
e
⊥
∼ Z
2
m
i
m
e
1/2
T
e
T
i
1/2
(12.141)
Comparing this with (12.138) we see that each of these factors now favours ion
transport over electron transport instead of the other way around. Hence, conclu-
sions in the parallel direction are reversed in the perpendicular direction where
energy transport is dominated by the ions.
On the other hand, comparison of ion and electron viscosities strongly reinforces
the conclusions based on (12.139). For the perpendicular viscosities we get
µ
i
2
µ
e
2
∼
1
Z
m
i
m
e
3/2
T
e
T
i
1/2
(12.142)
The stronger dependence on mass ratio and the weaker dependence on Z and
temperature ratio means that ions dominate momentum transport even more em-
phatically in the perpendicular direction than in the parallel direction.
Finally, turning to the non-diagonal transport coefficients we see that, with the
exception of ˜α
∧
∼ X
−3
e
, all have the asymptotic form
˜
L
∧
→−
1
X
α
, |X
α
|→∞ (12.143)
Not only are these coefficients larger by a factor |X
α
| than the perpendicular co-
efficients in this limit but they are also independent of any collision coefficients
arising from the collision term. When we substitute (12.143) in (12.121) we find
σ
∧
→ n
e
/eB
κ
e
∧
→ 5n
e
T
e
/2eB
κ
i
∧
→−5n
i
T
i
/2ZeB
µ
e
1
→ n
e
T
e
m
e
/eB
µ
i
1
→−n
i
T
i
m
i
/ZeB
(12.144)
showing no dependence on collisions at all, an effect also noted in Section 8.2.1.
Thus, in the strong B limit, the fluxes associated with these coefficients are non-
dissipative, arising entirely from the anisotropy introduced into plasma motion by
the magnetic field. Balescu shows, in fact, that in general the non-diagonal fluxes
make no contribution to entropy production and it is for this reason that there is no
contradiction implied by the negative coefficients κ
i
∧
and µ
i
1
.
Balescu compares his results with other treatments of transport theory. The most
important of these is that by Braginsky (1965) and there is remarkably good agree-
ment between Braginsky’s results and those of Balescu. A particularly important
feature of Balescu’s presentation which we have scarcely touched upon is the
12.7 MHD equations 501
role of entropy. Balescu shows how the second law of thermodynamics underlies
the classification of the moments and the interpretation of the results, many of
which are quite general and independent of the level of truncation of the moment
approximation.
12.7 MHD equations
We are now ready to take the third and final step in the progression from kinetic
equations to MHD equations. The major change from microscopic to macroscopic
description has already been established in Section 12.6.2 where we obtained a
closed set of equations entirely in terms of macroscopic variables. But substitution
of the transport equations (12.112)–(12.118) and the collision moments into the
hydrodynamic evolution equations (12.87), (12.89), (12.92) and (12.93), yields a
set of equations that is, for most practical purposes, far too complicated. Further
simplification is therefore essential.
To see how this may be done it is useful to summarize the full, closed set of
dissipative MHD equations. Starting with the hydrodynamic evolution equations
we have the continuity equation (12.87)
∂ρ
∂t
=−∇ · (ρu) (12.145)
The momentum balance equation (12.89), with qE neglected, is
∂(ρu)
∂t
=−∇ · (ρuu + PI) + j × B − ∇ · (
e
+
i
) (12.146)
The electron and ion temperature equations are obtained from (12.92) and (12.93).
Using (12.109) and (12.110) for the collision terms we have
∂T
e
∂t
=−
ˆ
u · ∇T
e
−
2
3
T
e
∇ ·
ˆ
u −
2
3n
e
e
: ∇u
−
2
3n
e
∇ · q
e
+
2
3en
2
e
j · R
e
−
2m
e
τ
e
m
i
(T
e
− T
i
) (12.147)
∂T
i
∂t
=−u · ∇T
i
−
2
3
T
i
∇ · u −
2
3n
i
i
: ∇u
−
2
3n
i
∇ · q
i
+
2Zm
e
τ
e
m
i
(T
e
− T
i
) (12.148)
where
ˆ
u = u −
m
i
Zeρ
j = u −
1
en
e
j (12.149)
Note that in the
e
term in (12.147) we have dropped the j component because the
product
e
· j is quadratic in small quantities.

502 The classical theory of plasmas
Using the approximation (12.90) together with (12.145) and (12.146) we can
combine (12.147) and (12.148) to obtain a single equation for the total plasma
pressure P
∂ P
∂t
=−u · ∇P −
5
3
P∇ · u +
5
3e
j · ∇T
e
−
2
3en
e
j · ∇(n
e
T
e
)
−
2
3
(
e
+
i
) : ∇u −
2
3
∇ · (q
e
+ q
i
) +
2
3en
e
j · R
e
(12.150)
The collision term R
e
and the privileged non-hydrodynamical moments are
given by (12.109) and the transport equations (12.112)–(12.114) and (12.120),
where the effective electric field
ˆ
E is given by (12.116) and the transport coeffi-
cients by (12.121). The final group of equations closing the set are the reduced
Maxwell equations (12.94)–(12.97).
This is the complete set of dissipative MHD equations but, as already remarked,
some further reduction is desirable for practical purposes. To make contact with the
MHD equations in Chapters 3–5, we rewrite the hydrodynamic equations (12.145)–
(12.150) as follows:
∂ρ
∂t
=−∇ · (ρu)
∂(ρu)
∂t
=−∇ · (ρuu + PI) + j ×B +[DISS]
∂T
α
∂t
=−u · ∇T
α
−
2
3
T
α
∇ · u + [DISS]
∂ P
∂t
=−u · ∇P −
5
3
P∇ · u +[DISS]
where only the non-dissipative terms are shown explicitly and in each equation
[DISS] represents all the dissipative terms, i.e. all the terms involving collisions.
Note that in most cases this is via the transport coefficients†.
Now recalling that the assumption underlying our approximation scheme is
that hydrodynamical moments are of order zero in = τ
α
/τ
H
while non-
hydrodynamical moments are of order one, it is easily seen that dissipative terms
are of order times the non-dissipative terms. The kind of further simplification
we might look for, therefore, would be to drop some or all of the dissipative terms.
However, this needs to be done with caution. The mathematical procedure used
in the derivation of the transport equations was a precise and correct linearization
in . Dropping dissipative terms which are of higher differential order than the
non-dissipative terms, on the other hand, may change completely the nature of
† In the following discussion we ignore the complication that in certain limits some of the transport coefficients
are independent of τ
α
.

12.7 MHD equations 503
the solutions. Put the other way round, the predictions of non-dissipative theory
may be very significantly changed by the inclusion of even the smallest amount
of dissipation. If dissipation is to be correctly treated as a small perturbation we
ought to use singular perturbation theory. We shall not pursue this but merely
remind the reader of what was said in Section 4.1. Narrow regions of very steep
gradients (sheaths) arise so that we should not expect a reduced set of equations to
be universally valid even for a given range of physical parameters.
12.7.1 Resistive MHD
The first simplification that we consider is the neglect of all dissipative terms except
electrical resistivity. The justification† for picking out this particular dissipative
term lies in the moment approximation scheme. Putting χ
α
= 0 in (12.101)
eliminates all the non-hydrodynamical moments except j which survives because
u
i
= u
e
. Resistive MHD is therefore equivalent to the 5M approximation.
Setting
q
α
= 0
α
= 0 (12.151)
in (12.113), (12.114) and (12.120) gives
α
kl
= 0 κ
α
kl
= 0 µ
α
p
= 0 (12.152)
for all k, l, and p. Referring back to the discussion of the transport coefficients in
the previous section we see that (12.152) can be achieved by a combination of the
|
α
τ
α
|→∞limit, to make non-parallel coefficients vanish, and the T
α
→ 0 limit
(see (12.135)–(12.137)) to make parallel coefficients vanish. Since τ
α
∝ T
3/2
α
/n
α
(see (12.122)) we are really talking about low pressure plasmas in strong magnetic
fields which are to be found in diffuse space plasmas such as the solar wind or
planetary atmospheres but not in fusion devices. Alternatively, from (12.121) we
see that (12.152) can be satisfied in the |
α
|τ
α
→ 0 limit, i.e. in a very strongly
collision-dominated plasma. Neither space nor fusion plasmas satisfy this condi-
tion.
Applying (12.151) to (12.109) gives
R
e
=
m
e
eτ
e
j (12.153)
and substituting this in (12.111) we get
m
e
τ
e
j + ej ×B = e
2
n
e
(E + u × B) + e∇(n
e
T
e
) (12.154)
† In view of the following discussion about the vanishing of the other coefficients, the retention of
σ
should be
regarded as an investigation of the effect of keeping one dissipative term.

504 The classical theory of plasmas
or, on solving for j,
j = σ ·
E + u × B +
1
en
e
∇(n
e
T
e
)
(12.155)
where
σ =
e
2
n
e
m
e
τ
e
1
1 + X
2
e
−X
e
1 + X
2
e
0
X
e
1 + X
2
e
1
1 + X
2
e
0
001
is identified as the electrical conductivity by comparison of (12.155) with (12.112).
Further simplification of Ohm’s law is obtained by assuming that the ion Larmor
radius r
L
i
is much smaller than the hydrodynamic length scale L
H
r
L
i
L
H
(12.156)
This is, in fact, the drift approximation which is good for space and fusion plasmas.
Then comparing the last two terms in (12.155) we find
|∇(n
e
T
e
)|
en
e
|u × B|
∼
T
e
eBuL
H
∼
r
L
i
L
H
c
s
u
T
e
T
i
1/2
(12.157)
where c
s
= (T
e
/m
i
)
1/2
is the ion acoustic speed. Assuming u ∼ c
s
and T
e
∼ T
i
we
can then drop the ∇(n
e
T
e
) term in Ohm’s law (12.155).
The final step in the simplification of Ohm’s law is to assume that |u
e
−u
i
|u
or
|j|en
e
|u| (12.158)
which seems reasonable in view of the fact that n
e
and u are hydrodynamical
moments of order zero while j is a privileged non-hydrodynamical moment of
order one in our approximation scheme. Here again (12.158) should be used with
caution. It clearly is not valid in static equilibrium problems where u = 0butj = 0.
Adoption of (12.158) means that the j ×B term in Ohm’s law can also be neglected
so that with (12.156) and (12.158) we get from (12.154)
j =
e
2
n
e
τ
e
m
e
(E + u × B) = σ
(E + u × B) (12.159)
which is the well-known simple form of Ohm’s law for a conductor moving with
velocity u.
The main point to note about (12.159) is that the conductivity tensor has been
reduced to a scalar. For strong magnetic fields this grossly over-estimates the
current perpendicular to the magnetic field for if we were to use (12.155) with

Exercises 505
∇(n
e
T
e
) neglected we know from our discussion of transport coefficients in the
previous section that σ
⊥
,σ
∧
→ 0asX
α
→∞. There is, therefore, no consistent
derivation of (12.159) and it must, at best, be regarded as a model equation adopted
for mathematical simplicity.
The derivation of the MHD equations is completed by applying (12.151),
(12.153), and (12.158) to (12.150) giving
∂ P
∂t
+ u · ∇ P =−
5P
3
∇ · u +
2(∇ × B)
2
3σ
µ
2
0
(12.160)
where (12.95) has been used to substitute for j in the last term. Note that T
e
no
longer appears in (12.160) and, since neither T
e
nor T
i
appear except implicitly
through P in the momentum equation (12.146), we can use (12.160) instead of
both (12.147) and (12.148).
In summarizing the set of resistive MHD equations it is useful to eliminate some
of the variables. Thus the current density j is determined by (12.95) and the electric
field E by (12.159). Then using (12.145), (12.95) and (12.151) the momentum
balance equation (12.146) becomes
ρ
Du
Dt
=−∇ P −
1
µ
0
B × (∇ × B) (12.161)
Finally, substituting (12.95) in (12.159) and (12.159) in (12.94) gives, in view of
(12.97),
∂B
∂t
= ∇ × (u ×B) +
1
µ
0
σ
∇
2
B (12.162)
The set has been reduced to (12.145) and (12.160)–(12.162) for the three hydro-
dynamical variables ρ,u and P and the magnetic field B. It is easily seen that
these correspond to the equations in Table 3.1 for γ = 5/3, in accordance with our
assumption that the plasma is a perfect gas having three degrees of freedom.
Exercises
12.1 Show that the Liouville operator L
N
is invariant under interchanges of like
particles and hence deduce that the generic N -particle distribution function
obeys the Liouville equation (12.5).
12.2 In the case of no external forces, compare the order of magnitude of the
terms in (12.23). Taking ω
−1
p
and λ
D
as characteristic time and length
scales show that the collision term (12.24) is of order g/ ff compared with
all the other terms.
12.3 By Fourier transform, or otherwise, solve (12.40) and hence obtain the
equilibium pair correlation function (12.41).
506 The classical theory of plasmas
12.4 Obtain the general moment equation (12.68) from the kinetic equation
(12.66) and show that the first three moments are given by (12.74)–(12.76).
Explain physically why there is no term containing B in (12.76).
12.5 Invert the set of equations (12.81)–(12.84) defining the one-fluid variables
to obtain the set (12.85).
12.6 Carry out the steps indicated in the text to transform the two-fluid moment
equations (12.74) and (12.75) to the equivalent set of equations (12.87)–
(12.91) in terms of one-fluid variables.
12.7 Under what circumstances might electron viscosity become significant?
How can this be explained physically?
12.8 Invert (12.154) to obtain (12.155). What is the physical significance of the
gradient term and how do you explain it?
