Boyd T.J.M., Sanderson J.J. The Physics of Plasmas

Подождите немного. Документ загружается.

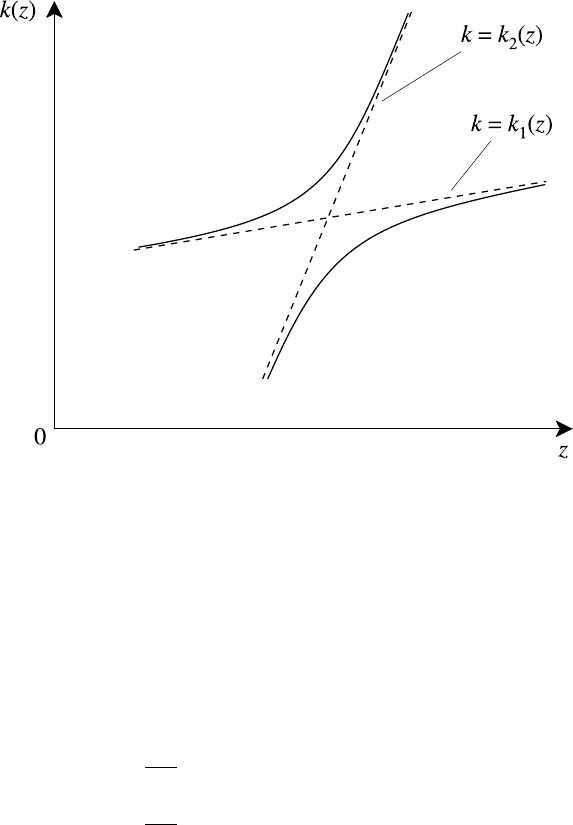
11.4 Linear mode conversion 437

Fig. 11.4. Coupling of modes k = k

, k = k

so that |φ

, |φ

denote energy ﬂuxes in the respective modes. Energy (ﬂux)

conservation then requires

|φ

+|φ

= constant (11.19)

A pair of differential equations satisfying (11.19) and reproducing the dispersion

relation (11.18) is then

dφ

− ik

(z)φ

= iχ

1/2

dφ

− ik

(z)φ

= iχ

1/2











(11.20)

Across the region of mode conversion one may assume

(z) = a(z − z

) k

(z) = b(z − z

)

which allows one of the amplitudes in (11.20) to be eliminated and the other deter-

mined by a second-order differential equation. This procedure leads to the Weber

equation with solutions expressed in terms of parabolic cylinder functions. The

asymptotics of these solutions are well known and a choice is made to represent an

incoming mode with two outgoing modes, leading to expressions for the transmis-

sion and mode conversion coefﬁcients in terms of the local dispersion relation and

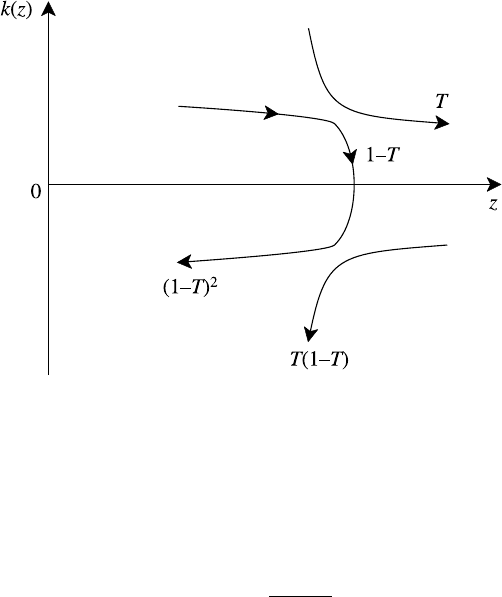
438 Aspects of inhomogeneous plasmas

Fig. 11.5. Behaviour at a cut-off near a mode conversion region.

gradients in the region of mode conversion. Cairns and Lashmore-Davies (1983)

showed that the energy transmission coefﬁcient is given by

T = exp



−

2πχ

|a − b|



(11.21)

where χ

denotes the value of χ at z = z

. The energy ﬂux in the converted wave

is (1 − T ) times the incident ﬂux.

In many cases of interest one of the modes suffers a cut-off near the mode conver-

sion point resulting in most of the energy associated with this mode being reﬂected

and coupled to oppositely directed waves. Thus in Fig. 11.5 an incoming wave is

shown approaching a C-point from the left. The fraction of energy transmitted is T

while the reﬂected fraction (1 − T ) couples to a mode propagating in the opposite

direction at an X-point. Here a fraction T undergoes mode conversion, giving a

fraction T (1−T ) of the incident energy ﬂux converted while the remainder (1−T )

is reﬂected. If we picture a wave approaching the X -point from the right we see

that the converted mode now propagates away from the cut-off and no reﬂection

occurs. The transmission coefﬁcient is unchanged but the converted fraction is now

1 − T . There is therefore an asymmetry between waves approaching from the left

(resulting in reﬂection) and waves from the right (no reﬂection). These results are

summarized in Table 11.1.

The appeal of this approach is that it side-steps the analytic complexity needed

to deal with equations such as (11.17). On the debit side the assumption that the

11.4 Linear mode conversion 439

Table 11.1. Transmission (T ), reﬂection (R) and mode conversion (C)

coefﬁcients for modes incident from right (r) and left (l) of the cut-off

resonance pair. Note η

∗

= πχ

/|a − b|.

TR C

= e

−2η

∗

= 0 C

= 1 − e

−2η

∗

= e

−2η

∗

= (1 − e

−2η

∗

)

= e

−2η

∗

(1 − e

−2η

∗

)

coupling coefﬁcient χ may be taken to be both spatially uniform and symmetric

between the modes is unlikely to be generally valid.

11.4.1 Radiofrequency heating of tokamak plasma

One important application of mode conversion is found in radiofrequency (rf)

heating of plasmas, particularly in tokamaks. We saw in Chapter 1 that the tem-

perature corresponding to the optimum reaction rate for D–T fusion lies in the

region 10–20 keV. The tokamak current heats the plasma through ohmic heating

(typically to temperatures of a few keV) but as the temperature rises, ohmic heating

becomes less and less effective and on its own is unable to heat the plasma to the

stage where alpha particle heating can sustain fusion. Additional power is needed

and this auxiliary heating in tokamaks is provided by neutral beam injection and rf

heating. In schemes for rf heating, power is fed into the plasma from waveguides

mounted in the wall of the torus. This power has then to be transported to the

R-point deep inside the plasma so that the issue of accessibility is critical to the

success of this form of heating. Various frequency ranges are used, including both

ion and electron resonances. Ion cyclotron resonance heating (ICRH) operating

in the range of a few tens of MHz has produced up to 16 MW of power in

JET.

To illustrate the importance of accessibility of the R-point consider a simple

model for electron cyclotron resonance heating (ECRH), in which an rf wave is

launched in the mid-plane of the torus, from either the inside or outside edge.

Typically ECRH operates at frequencies across the range 30–150 GHz. The plasma

density varies approximately parabolically across the torus, while the toroidal mag-

netic ﬁeld varies as 1/R. Since the wavelength of the electron cyclotron mode is

typically much less than the scale length of the tokamak plasma, a WKBJ repre-

sentation will be valid except at a cut-off and in the neighbourhood of a resonance.

Away from a resonance, wave propagation is adequately described by the cold

plasma, Appleton–Hartree dispersion relation so that we may make use of the CMA

diagram, introduced in Section 6.3.4. Figure 11.6 corresponds to regions 1, 3 and 5

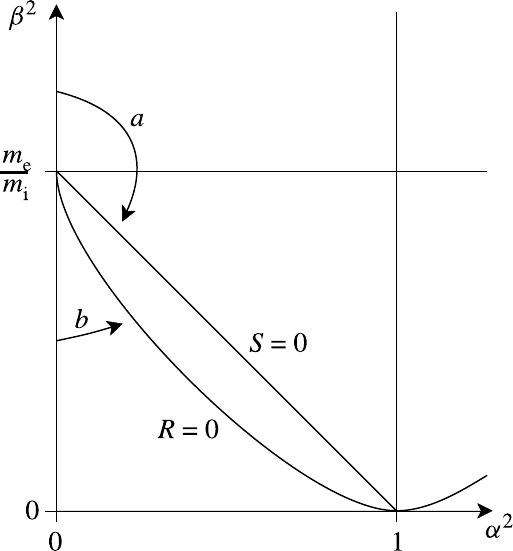
440 Aspects of inhomogeneous plasmas

Fig. 11.6. Section of the CMA diagram showing access to a resonance via path a in

contrast to path b which encounters a cut-off before the resonance.

in the CMA diagram, Fig. 6.12, and serves to highlight the role of both electron

density and magnetic ﬁeld in determining the propagation characteristics of these

modes. A wave propagating from the wall of a tokamak into regions of higher

density is represented by a point in the CMA diagram moving to the right, whereas

upward movement corresponds to an increase in the magnetic ﬁeld strength. A

wave that follows path a in Fig. 11.6 propagates from a region of higher to one

of lower magnetic ﬁeld and is capable of accessing the R-point, whereas one that

takes path b will fall foul of the C-point (R = 0) in propagating from a low density

region to one of high density. Thus a wave launched from the outside wall will be

reﬂected whereas one launched from the inside is able to reach the upper-hybrid

resonance. We stress that this picture is valid strictly for a cold, loss-free plasma.

For warm plasmas a crucial distinction is that electron cyclotron resonances at both

the fundamental and second harmonic now become dominant. Electrons interact

strongly with an RCP ﬁeld whereas this is shorted out in the cold plasma limit. A

concise discussion of the various schemes used in the rf-heating of plasmas may

be found in Cairns (1991).

11.5 Stimulated Raman scattering 441

11.5 Stimulated Raman scattering

We turn next to the ﬁrst of the topics chosen to illustrate aspects of the physics

of inhomogeneous plasmas. Stimulated Raman scattering was introduced in Sec-

tion 10.3.1 in model format. We now want to take this to a stage where it becomes

possible to use the model to interpret and understand observations of SRS. In

particular we shall examine the ways in which plasma inhomogeneity affects the

nature of the instability. Dephasing, the fact that phase-matching conditions can be

satisﬁed only over small regions of the plasma, is now a key concern. In addition,

non-local effects, such as the reﬂection of the Raman decay modes as the density

increases, can lead to feedback and this in turn can change the nature of the insta-

bility in important ways. In particular, a wave that is C-unstable in a homogeneous

plasma may become A-unstable in the presence of a density gradient.

11.5.1 SRS in homogeneous plasmas

Before turning to the inhomogeneous case it is helpful to retrieve some Raman

characteristics for a homogeneous plasma on the basis of the electron ﬂuid equa-

tions as opposed to the model equations used in Section 10.3.1. We begin by

representing the laser pump ﬁelds by

(r, t) = 2E

cos(k

· r − ω

t) B

(r, t) = 2B

cos(k

· r − ω

t) (11.22)

with ω

= ω

+ k

. Provided the laser intensity is not so high as to accelerate

electrons to relativistic velocities then the electron quiver velocity in the laser

electric ﬁeld is given by v

(r, t) = 2v

sin(k

· r − ω

t). For laser intensity

and wavelength λ

, the normalized quiver velocity, v

/c = (eE

/mω

c) =

4.27 × 10

−10

1/2

(Wcm

−2

)λ

(µm), is a critical parameter in characterizing para-

metric instabilities. A straightforward ﬁrst-order perturbation analysis of the elec-

tron ﬂuid equations (see Exercise 11.9) leads to a pair of coupled equations de-

scribing SRS in a homogeneous plasma:



∂

∂t

− c

∇

+ ω



=−

m

(11.23)



∂

∂t

− 3V

∇

+ ω



= n

∇

· v

) (11.24)

where ∂v

/∂t =−eE

/m and subscript s denotes the scattered wave.

Fourier analysing (11.23) and (11.24) leads directly to the Raman dispersion

relation

(ω

− ω

− 3k

)(ω

− ω

− k

) = k

(11.25)

442 Aspects of inhomogeneous plasmas

Physically, the laser pump in the presence of an electron density perturbation asso-

ciated with a Langmuir wave is the source of a non-linear current which generates

the Raman scattered light wave, given frequency and wavenumber matching. The

pump and scattered light wave beat to produce a ponderomotive force proportional

to ∇(E

· E

) and this in turn drives the density ﬂuctuation. This feedback loop

makes possible the development of SRS. For an instability to occur we need a pair

of complex conjugate roots. Accordingly we set ω = ω

+ iγ , ω

= ω

− iγ ,

where ω

= ω

+ 3k

, ω

= ω

+ k

, and |γ |ω

. Then from (11.25) the

maximum homogeneous Raman growth rate γ

is given by

2(ω

)

1/2

(11.26)

In the event that the phase matching conditions ω

= ω + ω

, k

= k + k

are not

exactly satisﬁed, mismatch will result in a growth rate γ<γ

In practice one needs to allow for damping of the Raman decay waves. The

Langmuir wave will be Landau damped but in a ﬂuid model we can only represent

this damping phenomenologically so that (11.25) is replaced by

(ω

+ 2iωγ

− ω

− 3k

)(ω

− 2iω

− ω

− 3k

) = k

where γ

, γ

denote damping coefﬁcients for the plasma and scattered light waves

respectively. The Langmuir wave may suffer collisional as well as Landau damping

so that in general γ

= γ

+ ν

/2, where ν

denotes the electron–ion collision

frequency. Damping of the light wave is purely collisional with γ

= ω

/2ω

Under resonance conditions

(γ + γ

)(γ + γ

) = γ

(11.27)

which determines the threshold for the onset of SRS

= (γ

)

1/2

(11.28)

and the Raman growth rate in terms of the maximum growth rate γ

and the wave

damping coefﬁcients, i.e.

γ =−

(γ

+ γ

) ±



(γ

− γ

)



1/2

(11.29)

11.5.2 SRS in inhomogeneous plasmas

In reality, plasmas in which stimulated Raman scattering occurs are inhomoge-

neous, often over short scale lengths. Under such conditions the extent of the

region of instability is localized on account of phase matching or the ﬁnite range

of the pump. Phase mismatch introduces a new loss mechanism on account of

11.5 Stimulated Raman scattering 443

the convection of wave energy away from the localized resonances. In practice,

convective loss is usually dominant over collisional and Landau damping. The

question that then arises is whether SRS is an absolute or a convective instability.

In other words, do the Raman daughter waves propagate away from the interaction

region after reaching some maximum amplitude or do they continue to grow within

the domain of instability? We shall ﬁnd that convective losses suppress the absolute

(temporal) growth found for the homogeneous plasma.

To keep the analysis as simple as possible we limit the plasma density inho-

mogeneity to one direction only, i.e. n

(r) = n

(x) and assume that the ions are

stationary. Moreover we consider only the case of normal incidence so that the

electric ﬁelds of both the incident and Raman scattered light waves are polarized

parallel to one another. The WKBJ representation of the laser pump may then be

written



(x, t)



√

(x)





cos ψ v

(x, t) =

√

(x)

y sin ψ

(11.30)

with ψ =



(x)dx − ω

t and ω

= ω

(x) + k

(x)c

. For convenience we

suppress the WKBJ swelling factor k

−1/2

, identifying the laser ﬁeld as the local

ﬁeld at the Raman resonance. The ﬁrst-order perturbation procedure proceeds as

in the homogeneous case and now generates the set of equations (in which primes

denote ∂/∂x and dots ∂/∂t):

˙n + [n

(x)v]



= 0

+ B



− µ

(x)v

= µ

env

(x, t)

˙v +

(x)



+ νv ˙v

+ νv

= 0

=−[v

(x, t)v

]



= 0 E



= 0











(11.31)

The structure of this set of equations shows the linear characteristics of the Lang-

muir wave and scattered light wave on the left-hand side with the non-linear cou-

pling through the action of the laser pump on the right. The scattered wave can

propagate either backwards (stimulated Raman back-scatter, SRBS) or forwards

(stimulated Raman forward-scatter, SRFS).

In general the set of equations (11.31) has to be solved numerically. To carry this

through and obtain time-asymptotic solutions we ﬁrst Laplace-transform (11.31).

It is straightforward to eliminate v and E

from the Laplace-transformed equations

444 Aspects of inhomogeneous plasmas

and convenient to cast the reduced set in normalized form. Times and veloci-

ties are normalized to ω

−1

and c respectively and in addition eE/mcω

→ E,

/mω

→ B

and e

, n)/m

→ (ω

(x), n). In this form the frequency

matching condition now reads ω + ω

= 1. The set of ﬁrst-order equations then

takes the form (see Barr, Boyd and Mackwood (1994))



+ n = 0 v



−

+ ν

= 0



+ [p

+ 2γ

+ ω

(x)]EB



− [p

+ p

ν + ω

(x)]v

= ω

(x)[v

(x)v

]



=−v

∗

(x)n











(11.32)

While the set of ﬁrst-order equations is convenient for numerical integration, one

can of course recover the coupled second-order equations for comparison with the

homogeneous plasma equations. These follow directly from (11.32) on eliminating

n and B

to give



+ [ω

+ 2iγ

ω − ω

(x)]E =−ω

(x)[v

(x)v

]



(11.33)



+ [ω

− 2iγ

− ω

(x)]v

= v

∗

(x)E



(11.34)

Here γ

(≡ γ

) = γ

+ ν/2, γ

= νω

/2ω

, p

= iω

, p

=−iω. WKBJ

solutions to (11.33) and (11.34) may be used provided the plasma density is only

weakly inhomogeneous in the sense described in Section 11.2 and provided the

Raman resonance is not in the neighbourhood of a turning point, i.e. at densities

well below the quarter-critical density. Consider a Raman resonance at x = x

where local wavenumber matching is satisﬁed, k

(x) = k(x) + k

(x), with slowly

varying amplitudes a

and a

deﬁned such that

E =

(x)

√

k(x)

exp





k(x)dx



(x)

√

(x)

exp



−i



(x)dx



(11.35)

where r = (kω

/ω)

1/2

, s = (k

/ω

)

1/2

evaluated at x = x

are constants.

The WKBJ equations reduce to (see Exercise 11.10)



+ (γ + γ

= γ

−iψ

(11.36)



+ (γ + γ

= γ

iψ

(11.37)

where ψ =



K (x)dx and K (x) = k

(x) − k(x) − k

(x) is the wavenumber

mismatch with K (x

) = 0; V

, V

denote the group velocities of the Langmuir and

Raman scattered waves respectively. Resonant coupling is lost once a signiﬁcant

phase shift builds up. For a homogeneous plasma ψ = 0 and the growth rate of

(11.29) is recovered. If we now combine the two WKBJ equations into a single

second-order differential equation for (say) a

, neglecting the spatial dependence

11.5 Stimulated Raman scattering 445

of V

and V

, setting a

= a exp(



α dx) where

α =−

[( p + γ

+ iKV

)/V

+ ( p + γ

)/V

]

one may show that



−



p + γ

+ iKV

−

p + γ





(

a = 0 (11.38)

For Raman back-scatter (V

< 0) from a localized source there is a regime of

convective Raman growth ( p = 0) provided

≤





(11.39)

Note that no convective growth is possible in the absence of damping. If the in-

equality sign in (11.39) is reversed, then stimulated Raman back-scatter (SRBS)

may grow absolutely with a growth rate

+ V

)

−



+ V



(11.40)

If we now allow a ﬁnite mismatch and consider in particular the case where this

is linear we ﬁnd that WKBJ theory shows that temporal growth is choked by con-

vection so that only spatial ampliﬁcation (convective gain) is possible. Expanding

K (x) about the Raman resonance and discarding wave damping, (11.38) becomes



−



−

+ iK



(0)x





(0) +

(

a = 0 (11.41)

For neither SRBS nor SRFS are solutions with p > 0 possible so that the

instability is always convective ( p = 0). Setting y = (K



(0))

1/2

x, (11.41) reduces



−

± λ



a = 0 (11.42)

where

λ =



(0)|V

≡



(0)L

(11.43)

deﬁning a threshold scale length L

for convective gain. In this form we see that the

solution depends only on the parameter λ; ±λ refer to SRBS, SRFS respectively.

Solutions to (11.38) may be found in terms of parabolic cylinder functions but all

that is needed here is an estimate of the maximum convective ampliﬁcation. The

446 Aspects of inhomogeneous plasmas

detuning of the Raman resonance condition is measured by the phase factor ψ(x)

and a resonance width l is deﬁned by



K (x)dx =





(0)x dx =

so that

l =



(0)

(11.44)

Only if l > L

will convective ampliﬁcation be signiﬁcant. A convective thresh-

old is conventionally taken as that intensity which results in a gain of exp(2π),

sometimes referred to as the Rosenbluth gain (Rosenbluth (1972)). Thus the gain

= exp



2πγ



(0)



(11.45)

and the convective threshold condition is expressed as



(0)

= 1 (11.46)

For a linear density proﬁle with ω

(x) = ω

(1 + x/L) the threshold for SRBS is

then





L = 1 (11.47)

Early in the evolution of SRS, waves grow at the absolute growth rate from

some initial localized noise source at the source point until such time as the waves

transit the resonance. At this point the waves become aware of the ﬁnite extent of

the resonance and temporal growth is saturated. Thereafter waves grow spatially

(amplify) as they propagate across the resonance with both decay waves ampliﬁed

in the back direction for SRBS and in the forward direction for SRFS. In this steady

state the localized resonance acts as a convective ampliﬁer.

For a given scattered frequency the resonant densities for SRBS and SRFS differ

by n ∼ n(V

), with SRFS occurring at the higher density. The two resonances

are not in fact independent though it has been conventional to treat them as if they

were. Wave propagation allows communication between resonances at different

locations, and this consideration in general results in quite distinct global behaviour

for the instability. Attention was ﬁrst drawn to the need for non-local models of

parametric instabilities by Koch and Williams (1984) and later described in detail

by Barr, Boyd and Coutts (1988), who solved the full system of SRS equations.

The SRBS, SRFS ampliﬁers couple through the propagation of a plasma wave up

the density proﬁle from the SRBS resonance to that for SRFS, together with the