Boyd T.J.M., Sanderson J.J. The Physics of Plasmas

Подождите немного. Документ загружается.

10.5 Collisionless shocks 407

Fig. 10.17. Laminar shock proﬁles. In the rest frame of the shock the arrows indicate the

direction of ﬂow from (1) upstream unshocked to (2) downstream shocked plasma. Shorter

wavelength waves either (a) trail behind or (b) forge ahead of the shock front.

ing to points on curves (a) or (b) but these travel at slower and faster phase speeds,

respectively, and as shown in Fig. 10.17 do not remain in the shock front. Thus,

steepening is limited by dispersion at a scale length ∼ k

−1

. If this is less than the

scale length for the onset of dissipation then the shock is ‘collisionless’ in that its

proﬁle is determined by wave dispersion rather than collisional dissipation. This

will obviously be the case for shocks in collisionless plasmas but may also occur

in collisional plasmas.

A second important difference between collisional and collisionless shocks re-

lates to the jump conditions across the shock. The state of a collisional plasma

is determined by its density, ﬂow velocity and temperature so that conservation

of mass, momentum and energy means that the jump conditions are independent

of shock structure. No such claim can be made for a collisionless shock. Even

if the unshocked plasma is in an equilibrium state represented by a Maxwellian

distribution there are too few collisions to re-establish a Maxwellian in the shocked

plasma. So, although mass, momentum and energy must still be conserved, the ﬁnal

state of the plasma cannot in general be represented in terms of density, velocity

and temperature alone; mathematically, the moment equations do not form a closed

set. In particular, anisotropies created in the shock, in the absence of collisions,

may persist into the downstream plasma. A useful aspect of this is that observation

of the downstream plasma may yield information about the shock structure; for

example, it may suggest which unstable waves are responsible for the turbulent

dissipation.

A third point of sharp contrast shows up in shock structure. Collisions convert

the upstream state to the downstream state within a collisional shock which is about

a mean free path in dimension. Thus, particles from the upstream state cannot

penetrate the shock without undergoing conversion to the downstream state so that

408 Non-linear plasma physics

the two states remain physically separated. How is this separation maintained in

collisionless shocks?

One possible mechanism is to have a magnetic ﬁeld perpendicular to the di-

rection of propagation of the shock of sufﬁcient strength that the Larmor radius

 L

, where L

is the shock thickness. If this is not the case, or if the magnetic

ﬁeld has a component parallel to the direction of shock propagation, fast particles

can cross the wave-front where their free energy may trigger instabilities leading

to turbulent dissipation. Thus, a second possibility is that the shock may have a

width of the order of the mean free path for turbulent dissipation. A special case

is that of low β shocks with shock velocity V

greater than the magnetoacoustic

speed; here the number of particles with speed greater than V

will be exponentially

small.

As with collisional shocks, kinetic theory is necessary for a rigorous description

of shock structure though transport equations, with ‘ﬁtted’ turbulent transport co-

efﬁcients replacing the collisional coefﬁcients, are frequently used. In two special

cases, however, the use of a ﬂuid description may be justiﬁed (in contrast with

collisional shocks where, on account of the shock width, there is no rigorous

justiﬁcation):

(i) the cold plasma approximation, where thermal velocities are very much

smaller than phase velocities, i.e. the thermal spread in particle velocities

is unimportant and all particles of a given type experience the same local

force due to the self-consistent ﬁelds.

(ii) the small Larmor radius (strong magnetic ﬁeld) approximation in which

particles move with the ﬁeld lines.

A ﬁnal comment concerns energy and entropy in collisionless shocks. Ordered

energy may be in the plasma ﬂow, the magnetic ﬁeld, or coherent oscillations.

Various energy conversions are possible and since we are dealing with collective

interactions it is neither obvious nor necessarily true that an increase in entropy

will accompany a change of state. Examples of isentropic transitions are solitons

which pass through the plasma leaving the ﬁnal state identical to the initial state.

Alternatively, the ﬁnal state may contain coherent plasma oscillations. We shall

see, however, that in both cases a small amount of dissipation (collisional or tur-

bulent) will convert these to shock transitions with increased entropy in the ﬁnal

state.

10.5.1 Shock classiﬁcation

The most general description of a collisionless plasma is given by the Maxwell–

Vlasov system of equations and for applications to collisionless shocks it is useful

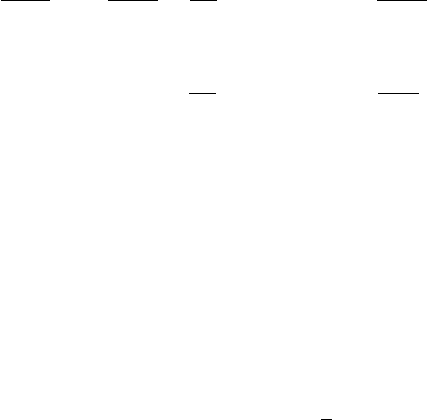
10.5 Collisionless shocks 409

to make a formal separation of the dependent variables f , E and B into their aver-

age and ﬂuctuating components. By an average quantity φ we mean an ensemble

average and δφ = φ −φ is the ﬂuctuation about this. In practical terms what this

means is that φ represents an average shock proﬁle and δφ a random or turbulent

variation superimposed on it. For the moment we make no assumptions about the

relative magnitudes of φ and δφ.

Since δφ=0, on taking the ensemble average the Maxwell equations being

linear in f , E and B are unchanged except for the substitution of φ for φ while

the Vlasov equation for f

(α = i, e) becomes

∂ f



∂t

+ v ·

∂ f



∂r

[E+v ×B] ·

∂ f



∂v

= C

(10.75)

where

=−



[δE + v × δB] ·

∂δf

∂v



(10.76)

Writing the Vlasov equation in this way shows that the ﬂuctuations act like a

‘collision’ term in the kinetic equation for  f

. Note, however, that C

involves

interactions between the ﬂuctuating ﬁelds and distributions, i.e. particles. Because

of this, particle momentum and energy are not conserved in contrast with the action

of the classical collision term. Assuming no particles are created or destroyed we

have



dv = 0

but





dv = 0





dv = 0 (10.77)

A further consequence of (10.77) is that C

does not cause  f

 to relax to a

Maxwellian distribution, thus producing the contrast with collisional shocks con-

cerning the jump conditions noted in the previous section.

In principle we can now proceed to a ﬂuid description by deﬁning the plasma

ﬂuid variables in terms of  f

 rather than f . However, aside from the usual

problem of truncating the inﬁnite set of moment equations based on (10.75), one

has the additional problem of closing the set of equations for the ﬂuctuations δφ

which are needed for evaluating C

. These are obtained from the Maxwell–Vlasov

equations by subtracting the ensemble averaged equations but we shall not pursue

this formal approach.

Instead let us consider the separation φ =φ+δφ in terms of shock clas-

siﬁcation. Shocks in which the ﬁeld and plasma variables change in a coherent

manner are referred to as laminar; any turbulence present is on a scale small

410 Non-linear plasma physics

enough not to destroy the coherent proﬁle. If there is no turbulence (C

= 0) then

there is strictly speaking no shock (unless we introduce collisional dissipation) and

the solutions of the equations correspond either to solitary waves or undamped

oscillations. Non-zero C

, but such that the turbulence is weak and occurs on

a scale which is small in wavelength compared with the shock thickness, gives

rise to dissipation and hence to true shock solutions. Such a shock will appear

laminar on a scale longer than the wavelength of the micro-turbulence. Typical

proﬁles are shown in the shock rest frame in Fig. 10.17. Short wavelength oscil-

lations damp out either (a) downstream or (b) upstream in accordance with the

dispersion curves in Fig. 10.16. The basic procedure here is to treat C

as a small

perturbation.

As we shall see, the investigation of laminar shocks shows that they can exist

only within certain parameter ranges. Beyond these ranges the ﬂuctuations become

large, C

plays a dominant role and the shock loses its laminar proﬁle. Such cases

are referred to as turbulent shocks

Note, however, that there is no sharp demarcation between laminar and turbulent

shocks. Rather, these are opposite ends of a spectrum embracing many possible

structures. For example, if the turbulent ﬂuctuations are small in amplitude but with

a wavelength comparable with the shock thickness then this cannot be regarded

as micro-turbulence and the shock is a mixture of laminar and turbulent structure.

Other complications arise from the dispersive limitation of shock steepening giving

rise to precursors and wakes. Also, the spread in particle velocities can lead to

trapping and acceleration culminating in the emission of supra-thermal particles.

All of these phenomena are discussed theoretically at various levels by Tidman and

Krall (1971). Experimentally, the Earth’s bow shock, which has been extensively

investigated by satellite observations, is a rich source of all kinds of collisionless

shock. Here we shall present only a few well-established results starting with the

simplest mathematical descriptions and proceeding step by step to widen their

applicability.

As noted in Section 5.6.1, shocks may also be classiﬁed by the angle θ between

their direction of propagation and the magnetic ﬁeld B

in the unshocked plasma.

Thus, shocks may be perpendicular (θ = π/2), parallel (θ = 0),oroblique (0 <

θ<π/2). We shall see that perpendicular shocks are in general more amenable

to analysis. This is not surprising since, as already noted, a magnetic ﬁeld at right

angles to the ﬂow can of itself be an effective agent for separating the upstream

and downstream plasmas. On the other hand, in oblique and parallel shocks the

magnetic ﬁeld can act as a particle conduit between the upstream and downstream

plasmas so that the physics of these shocks (and consequently the mathematics) is

immediately more complex. We illustrate procedure, therefore, with perpendicular,

laminar shocks.

10.5 Collisionless shocks 411

10.5.2 Perpendicular, laminar shocks

To start with as simple a model as possible let us consider non-linear wave propa-

gation in a cold plasma. If we put C

= 0 initially then we know that the deﬁnitions



 f

dvu



v f

dv

lead to the cold plasma wave equations

∂n

/∂t + ∇ · (n

) = 0

(

∂/∂t + u

· ∇

)

= e

(E + u

× B)/m



(10.78)

on taking the ﬁrst two moments of (10.75).

Linear wave solution

Before we seek ‘shock’ solutions of these equations it is of interest to identify the

linear wave which, through dispersive limitation of non-linear steepening, produces

the steady, ﬁnite amplitude wave. In Section 6.3.3 we showed that there were

two waves which propagate perpendicular to the equilibrium magnetic ﬁeld. One

of these, the O mode, is a transverse electromagnetic wave which propagates at

frequencies above the plasma frequency. The other wave, the X mode, has three

branches and it is the lowest frequency branch (0 <ω<ω

) which produces the

non-linear wave we shall investigate.

Assuming 

 ω

, i.e. v

 c

, from (6.36), (6.43) and (6.44) we have

≈ ω

and ω

≈|



1/2

so that, on using (6.29), (6.60)

becomes

−|



− ω

The solution of this equation in the frequency range 0 <ω<|



1/2

≈

(1 + k

/ω

)

1/2

(10.79)

This is the dispersion relation of the compressional Alfv

en wave which appears as

the lowest branch of the X mode in Fig. 6.7. It is more commonly referred to by its

ﬁnite β name as the magnetoacoustic (or magnetosonic) wave. The points to note

are:

(i) for k → 0, ω/k ≈ v

= const.,

(ii) dispersion becomes signiﬁcant for k ∼ k

= ω

/c,

(iii) waves with k > k

have phase speeds ω/k <v

412 Non-linear plasma physics

Fig. 10.18. Non-linear compressional Alfv

en wave.

It follows that a ﬁnite amplitude wave generated by non-linear wave steepening

and limited by dispersion would have a wave-front, of width L

∼ c/ω

, travelling

with speed v

ahead of shorter wavelength modes as shown in Fig. 10.18.

Non-linear wave solutions

Calculations to ﬁnd the structure predicted in Fig. 10.18 were ﬁrst carried

out by Adlam and Allen (1958), Davis, L

ust and Schl

uter (1958) and, subse-

quently, Sagdeev (1966). It is Sagdeev’s calculation, as presented by Tidman and

Krall (1971), that we follow. We suppose that a steady proﬁle has been achieved

between non-linear wave steepening and dispersive limitation and we look for a

time-independent, laminar solution of (10.78). Thus, we assume all variables are

functions of x only and have values in the upstream region (x →−∞) given by

(−∞) = Zn

(−∞) = n

(−∞) = u

(−∞) = (u

, 0, 0)

B(−∞) = (0, 0, B

)

E(−∞) = (0, u

, 0)











(10.80)

It then follows from the Maxwell equations that

(x) = 0, E

(x) = u

Also, since the equations for B

and u

αz

decouple from the rest we may look for a

solution in which these variables are zero. The remaining equations give

= Zn

= n

(10.81)

αx



αx

+ u

αy

B)(α= i, e) (10.82)

αx



αy

− u

αx

B)(α= i, e) (10.83)

10.5 Collisionless shocks 413



= µ

e(n

− Zn

) (10.84)



(Zn

− n

) (10.85)

Now assuming quasi-neutrality we put Zn

= n

in (10.81) and (10.84) but not

in (10.85) where the small inequality produces the electric ﬁeld which, as we shall

see later, decelerates the ion ﬂow. The quasi-neutrality condition is |Zn

−n

|n

which can be shown a posteriori to be 

 ω

, as assumed in the linear wave

calculation. With this assumption it follows from (10.81) and (10.83) that

= u

(10.86)

say, and

=−

(10.87)

Substituting these results in (10.82) and subtracting the electron equation from the

ion equation then gives

=−Bu

on ignoring terms of order m

. Likewise, multiplying (10.82) by m

(α =

i, e) and subtracting eliminates the electric ﬁeld to give to the same order



= B(u

− u

) =−



where the second equality follows from (10.84). Substituting for n

from (10.81)

and (10.86) and integrating we get

= 1 −







− 1



(10.88)

where M

= u

is the Mach number and v

= B

/(µ

/Z )

1/2

is the

upstream Alfv

en speed. This equation shows how the ﬂow velocity decreases as

the magnetic ﬁeld increases.

From (10.81), (10.84) and (10.87) we get





1 −



− 1





(10.89)

where terms of order m

have again been ignored and (10.88) has also been

used. Now all variables are, at least implicitly through (10.88) and (10.89), ex-

pressed in terms of the magnetic ﬁeld B(x). To complete the calculation, therefore,

we need an equation for B(x). This is obtained from (10.84) using (10.83) to get



) = µ

) =−

− u

414 Non-linear plasma physics

and hence, using (10.88) and (10.89),



1 −



− 1





1 −



− 1





(B − B

)



1 −

B(B + B

)



Multiplying this equation by dB/dx gives an exact differential on the left-hand side

and on integration we get





+ (B) = 0 (10.90)

where

(B) =−





(B − B

)



1 −

(B + B

)



(



1 −



− 1



(10.91)

Although (10.90) can be formally integrated to obtain x as a function of B it is

more instructive to discuss it directly since it has the form of an energy equation

for a particle in a potential well; B has the role of space coordinate and x is the

‘time’. When B = B

, the ‘potential energy’ (B) =−



)

and it is easy to

show that initially it decreases as B increases. Thereafter it reaches a minimum

and then increases with B and we can ﬁnd the range of values of B by examining

the motion of the imaginary particle in the potential well. There are two possible

cases depending on whether B



is zero or not and these are both represented in Fig.

10.19.

In case (a) (B



= 0) the ‘particle’, which starts off at the point shown with

kinetic energy



)

, will travel to B

max

, at which point its kinetic energy is

exhausted, and then it will roll back till it reaches B

min

. Thereafter it will oscillate

back and forth between these two points so the structure of B(x) is as shown in (c),

i.e. a train of ﬁnite amplitude waves of ﬁnite wavelength.

In case (b) the particle again travels from its initial point B

, here also its

minimum point, to its maximum point and back again, but because it returns to

an equilibrium point it does not oscillate further. In fact, it takes an inﬁnite ‘time’

(distance x) on both stages of its journey so the structure of B(x) in this case is

a soliton, as shown in (d). Neither of these solutions corresponds to a shock but

the introduction of dissipation of some kind will convert both to laminar shock

proﬁles. However, before we demonstrate this let us examine the soliton solution a

little more closely to illustrate some of its parametric properties.

10.5 Collisionless shocks 415

Fig. 10.19. Potential function for non-linear compressional Alfv

en wave.

First of all, with B



= 0, it is easily seen from (10.91) that 



) = 0 so that

near B

(B) ≈

(B − B

)





where







(B)



B=B

=−



1 −



It follows that the asymptotic solution of (10.90) is

B − B

∼ e

∓|



1/2

(x →±∞)

This shows the slope predicted by the linear theory but with a modifying factor

(1 − 1/M

)

1/2

which is dependent upon the amplitude of the wave. This result

L ∼

(1 − 1/M

)

1/2

(10.92)

for the breadth of the wave-front was obtained by Adlam and Allen (1958).

416 Non-linear plasma physics

Fig. 10.20. Validity diagram for undamped non-linear wave solution.

Next, writing B

for B

max

and noting that (B

) = 0 it follows from (10.91)

that

= B

(2M

− 1) (10.93)

Also, from (10.88), (10.90) and (10.91) we see that u

→ 0 and dB/dx →∞as

(B/B

) →

+ 1 (10.94)

The solution breaks down, therefore, if

+ 1 ≤ 2M

− 1, i.e. M

≥ 2. This

is illustrated graphically in Fig. 10.20; for a valid solution the (B

) = 0 curve

must lie below the u

= 0 curve. For waves with M

≥ 2 dispersive limitation

of steepening fails as the limit (10.94) is approached. It is easily veriﬁed that

, E

→∞as well as dB/dx in this limit. Physically, it is clear that dissipative

limitation will take over in response to these large gradients and we shall now

show that the introduction of dissipation converts these isentropic, non-linear wave

solutions into shocks.

Shock solutions

Dissipation is likely to arise via drift instabilities driven by the free energy in the

current ﬂowing parallel to the wave-front. Indeed, this is how one attempts to arrive

at a self-consistent model of a perpendicular shock. The jump in B

requires a