Boyd T.J.M., Sanderson J.J. The Physics of Plasmas

Подождите немного. Документ загружается.

10.5 Collisionless shocks 417

which feeds energy into unstable drift waves thereby providing the turbulent

dissipation and consequent increase in entropy. A proper treatment clearly requires

kinetic theory but we can model this behaviour very simply by re-introducing

the ‘collision’ term C

in (10.75) so that ﬁrst-order velocity moments of C

now

appear in the momentum equations. For simplicity, we shall introduce these only in

(10.83) since it is only in the y direction that there is an appreciable drift between

ions and electrons. Furthermore, we shall assume, despite the observations made in

Section 10.5.1 (see (10.77)), that the net loss of momentum from particles to ﬁelds

is negligible, that is





dv ≈ 0

Neither of these simplifying assumptions can be rigorously justiﬁed since unstable

waves are capable of transferring momentum in all directions and from particles

to waves. However, they are not unreasonable in the limit of weak turbulence and

enable us to make analytic progress revealing, qualitatively at least, the effect of

dissipation on the isentropic solutions.

The analysis proceeds as before but there now appears an extra term in the

differential equation for B(x) which becomes





(B −B

)



1 −

B(B + B

)





dv (10.95)

Deﬁning a (constant) ‘collision’ frequency ν by



dv = νn

and a ‘stretched’ space coordinate ξ by

x = ξ u

(10.95) becomes, on substituting for u

from (10.89),

B(ξ)

dξ

=−

dφ(B)

−

dB(ξ )

dξ

(10.96)

where

φ(B) =

(B − B

)



(B + B

)

− 1



(10.97)

Comparing (10.96) with

¨x =−

− ν ˙x

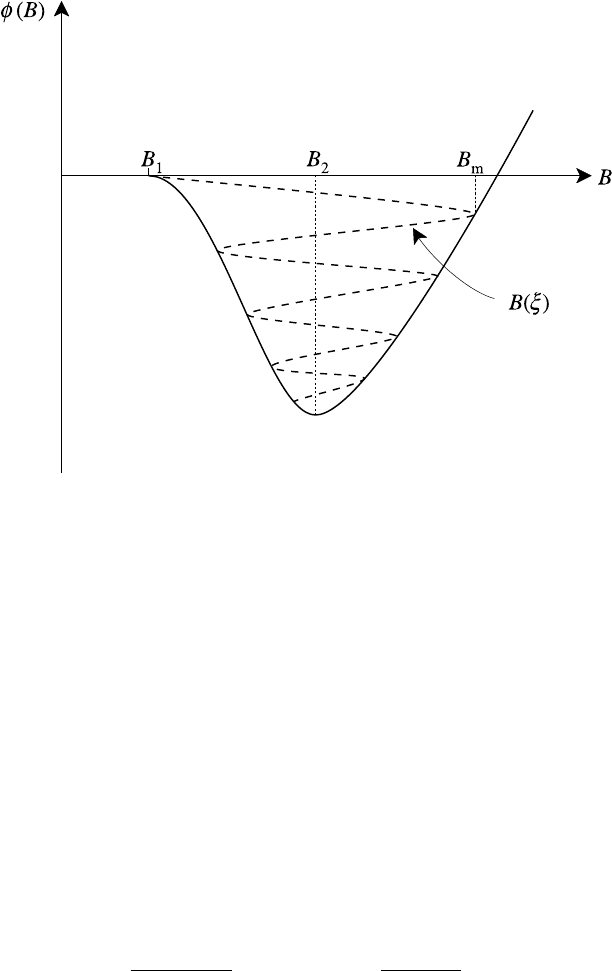
418 Non-linear plasma physics

Fig. 10.21. Damped motion in a potential well.

we see that it is analogous to damped motion in a potential well. This is sketched in

Fig. 10.21. The dashed lines join up the successive turning points and trace out the

values of B(ξ) as damping decreases the total energy of the imaginary particle in

the potential well; B

(< B

) is now the maximum value attained by the magnetic

ﬁeld and B

is its ﬁnal value. The corresponding structure of the magnetic ﬁeld is

shown in Fig. 10.22; the dashed line here shows the soliton solution in the absence

of dissipation. There are now two scale lengths associated with the solution, c/ω

is still the width of the leading edge of the shock but this is followed by a trail

of waves of decreasing amplitude over a decay length of order u

/ν. Provided the

damping is weak we may regard the structure as a train of solitons the breadth of

which successively increases in accordance with (10.92).

Since B

< B

, wave-breaking (u

→ 0) no longer occurs as M

→ 2 and

the shock solution exists beyond this limit. Indeed, one might suppose that by

increasing ν one could ensure a valid shock solution for arbitrary M

.Asν →∞,

→ B

= B

[

+ 1/4 − 1/2] < B

+ 1, which is the value of

B at which u

= 0 as given by (10.94). However, this would be stretching the

validity of this simple model beyond reasonable limits. Not only have we supposed

that the damping is weak but we have ignored the fact that dissipation inevitably

leads to plasma heating. A dissipative, cold plasma model is not self-consistent.

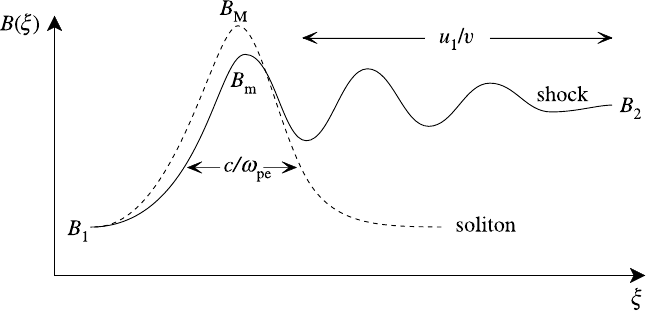
10.5 Collisionless shocks 419

Fig. 10.22. Structure of the magnetic ﬁeld in the shock solution.

Tidman and Krall (1971) discuss at some length shock solutions obtained from

the warm plasma wave equations with damping and ﬁnd that ﬁnite β limitations on

outweigh the effect of dissipation with the result that the critical Mach number,

now a function of β and ν, is less than 2.

The usefulness of ﬂuid equations for the description of ﬁnite temperature effects

is limited. Any spread in particle velocities means that some ions will have sufﬁ-

cient kinetic energy to pass over the potential hill presented by the electric ﬁeld but

others will not. These slower ions are therefore reﬂected back upstream so that one

has, in effect, two ion ﬂuids rather than one. Furthermore, the reﬂected ions are

turned by the Lorentz force upstream and re-enter the shock where they may again

be transmitted or reﬂected – they bounce off the shock front, as illustrated in Fig.

10.23, until they have gained sufﬁcient energy to pass through. Since the dynam-

ics of the ions is dependent upon their velocity distribution a kinetic description

becomes essential.

We are now ready to construct a self-consistent model of a laminar, perpen-

dicular shock. A ﬂuid model based on a strong magnetic ﬁeld (i.e. small Larmor

radius) is valid provided the scale length L  r

. For ions this would imply

a much stronger condition, β

 m

, than for electrons, β

 1, when

L = L

∼ c/ω

, the width of the wave-front produced by dispersive limitation of

wave steepening. Consequently, the ordering is

 L

 r

and the effect of the electric ﬁeld, due to charge separation in the shock, is different

for electrons and ions. The electrons experience an E × B drift in the shock front,

establishing the current j

. The ion orbits are, however, essentially straight lines

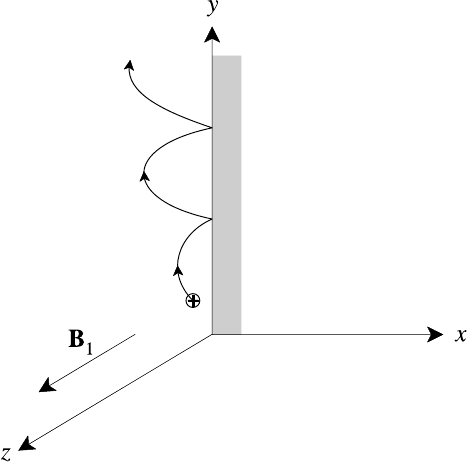
420 Non-linear plasma physics

Fig. 10.23. Slow ion reﬂection off shock front.

so that the main effect of the electric ﬁeld E

is to slow the ﬂuid (ion) ﬂow. The

current j

is consistent with the increase in B(x) and drives the drift instabilities

which provide the dissipation to turn ﬂow energy into thermal energy.

As we approach the critical Mach number (or increase β

), some ions are re-

ﬂected before eventually passing through the shock. These ions drag electrons with

them and this plasma and the magnetic ﬁeld lines that are drawn out with it form a

‘foot’ in the magnetic ﬁeld structure in front of the main ﬁeld jump, as illustrated

in Fig. 10.24. This foot, which has a width ∼ v

/

∼ c/ω

, is observed as

the critical Mach number is exceeded since the fraction of reﬂected ions becomes

signiﬁcant. As M

increases, the foot dominates and L

∼ c/ω

. Dissipation in

supercritical shocks is caused by ion streaming instabilities feeding on the energy

in the reﬂected ions.

The same procedure can be used to discuss oblique (and parallel) shocks but

for the reasons already mentioned, the analysis is complicated. Often transport

equations with ﬁtted ‘turbulent’ transport coefﬁcients are used to obtain numerical

calculations of shock structure. The main interest in this ﬁeld is related to plane-

tary and astrophysical shocks and much data has been collected about the Earth’s

bow shock which varies in nature between quasi-perpendicular and quasi-parallel.

While this makes it a very interesting object it also makes the interpretation of data

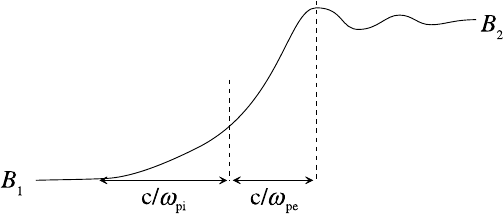
10.5 Collisionless shocks 421

Fig. 10.24. Shock structure for supercritical shocks.

difﬁcult. Observations, usually made by groups of satellites so that correlations

may be recorded to facilitate interpretation, have not only estalished the existence

of the bow shock but have also yielded information about the electron and ion

foreshocks. The ion foreshock, comprising reﬂected ions with energies of a few

keV, is the shock foot to which we have already referred. The electron foreshock

consists of energetic electrons (1–2 keV) created at the quasi-perpendicular shock

and travelling back into the solar wind along the ﬁeld lines. A possible mechanism

for this phenomenon is discussed in the following section.

10.5.3 Particle acceleration at shocks

The presence of electron and ion populations in the upstream plasma with energies

far greater than the mean energy of the solar wind particles is a well-established

feature of the Earth’s bow shock. These particles are produced as a result of re-

ﬂection and acceleration by the shock and there are any number of mechanisms

which may be responsible. In the last section we noted the reﬂection of ions by the

electric ﬁeld in a perpendicular shock but when there is a component of magnetic

ﬁeld along the shock normal it is very easy for both ions and electrons to return

into the solar wind should conditions in the bow shock propel them back along the

ﬁeld lines.

It is easiest to discuss this phenomenon in the de Hoffmann–Teller (HT) frame of

reference introduced in Section 5.6.4. In the HT frame, by deﬁnition, the upstream

velocity v

and magnetic ﬁeld B

are parallel, a situation that is brought about by

applying a Lorentz transformation from the shock frame to a frame that is moving

parallel to the shock face with an appropriate velocity v

. Thus, the incident (u)

and reﬂected (v) particle velocities may be resolved

u = u



+ v

(10.98)

v = v



+ v

(10.99)

422 Non-linear plasma physics

where u



and v



are both guiding centre velocities along B

. Depending upon the

reﬂection mechanism, the magnetic moment may or may not be conserved so we

write



=−αu



(10.100)

where α is a positive constant.

Since there is no electric ﬁeld, E

=−v

× B

= 0, in the upstream plasma,

kinetic energy is conserved so that



+ u

⊥

= v



+ v

⊥

(10.101)

where u

⊥

and v

⊥

are, of course, the components of the incident and reﬂected

velocities perpendicular to B

, i.e. the speeds of rotation around the ﬁeld lines.

From (10.98)–(10.100) it follows that

− v

= (1 − α



+ 2(1 + α)u



· (u − u



)

and hence,

= u

+ (1 + α)



− 2(1 + α)u



· u

Thus, in the rest frame of the shock, the ratio of reﬂected to incident kinetic energy

= 1 + (1 + α)



− 2(1 + α)



· u

(10.102)

Then, if θ

is the angle between vectors a and b,wehaveu



cos θ

= u cos θ

and u



· u = u



u cos θ

so that (10.102) becomes

= 1 + (1 + α)

cos

− 2(1 + α)

cos θ

Clearly, this ratio can take a wide range of values, but for quasi-perpendicular

shocks cos θ

≈ 0, making the second term dominant and leading to large in-

creases in reﬂected particle energy.

Note that the reﬂected ‘thermal’ energy represented by v

⊥

is given from (10.100)

and (10.101) by

⊥

= (1 −α



+ u

⊥

≈ (1 −α



Exercises 423

in the cold solar wind approximation (u

⊥

≈ 0) showing that α ≤ 1 for physical

solutions, there being no change in thermal energy for α = 1.

Exercises

10.1 What are the small parameters that justify use of linear theory in (i) particle

orbit theory, (ii) cold plasma wave theory, (iii) warm plasma wave theory,

(iv) MHD, and (v) kinetic theory? Give examples of the breakdown of

linear theory despite the smallness of the appropriate parameters.

10.2 Carry out the steps indicated in the text to obtain (10.6), (10.8) and (10.10).

Show that the spectral energy density E(k, t) deﬁned by (10.12) satisﬁes

(10.13) and explain the physics of this equation.

10.3 With reference to Fig. 10.2, explain the relationship between the energy

level of an electron and its phase space trajectory. Why is it the resonant

electrons that are trapped? How does this impose a restriction on the valid-

ity of linear Landau theory and what is this restriction?

10.4 What is the essential property of the ballistic terms which gives rise to

plasma echoes?

Show that if waves exp −i[k

x − ω

t] and exp −i[k

(x −l) − ω

t] are

generated at grids separated by a distance l a plasma echo may appear at a

point x downstream where x = ω

l/(ω

− ω

Note that the echo will appear only if ω

>ω

. How do you explain this

physically?

10.5 Starting from the coupled harmonic oscillator equations (10.28) derive the

set of equations (10.32) for the amplitudes a

, a

. Verify (10.34) and

show that it expresses conservation of energy. Why is energy conserved?

Obtain the Manley–Rowe relations (10.35).

10.6 Derive (10.39) from (10.36) by allowing for a frequency mismatch ω =

− ω

. Show that this leads to an increase in the threshold for

instability given by (10.41) and exlain why.

10.7 Obtain (10.71) and (10.72) from the one-dimensional Zakharov equations.

Show that the non-linear Schr

odinger equation (10.74) has a solution of

the form E(z, t) = e

it

f (z) where f (z) = (2)

1/2

sech(

1/2

z). Interpret

this solution physically.

10.8 Carry out the steps indicated in the text to show that the magnetoacous-

tic wave with dispersion relation (10.79) arises on the lowest frequency

branch of the X mode.

With reference to Fig. 10.18, explain the properties of a ﬁnite amplitude

magnetoacoustic wave.

424 Non-linear plasma physics

10.9 Explain why a laminar, perpendicular shock has a thickness which is much

less than the ion Larmor radius but much greater than the electron Larmor

radius. What is the signiﬁcance of this for the motion of ions and electrons

through such a shock? How does this lead to a self-consistent model for

these shocks?

Aspects of inhomogeneous plasmas

11.1 Introduction

In this chapter we turn to a consideration of the physics of inhomogeneous plasmas.

Since virtually all plasmas whether in the laboratory or in space are to some degree

inhomogeneous, all that can be attempted within the limits of a single chapter

is to outline some general points and illustrate these with particular examples.

Throughout the book we have dealt in places with plasmas which were inhomoge-

neous in density or temperature and conﬁned by spatially inhomogeneous magnetic

ﬁelds. In the case of the Z -pinch the high degree of symmetry allowed us to ﬁnd

analytic solutions in studying the equilibrium. By contrast for a tokamak, even

with axi-symmetry, solutions to the Grad–Shafranov equation could only be found

numerically. Indeed the only general method of dealing theoretically with problems

in inhomogeneous plasmas is by numerical analysis.

Nevertheless useful analytic insights may be gained in two limits. In the ﬁrst,

plasma properties change slowly in the sense that for an inhomogeneity scale length

L and wavenumber k, kL  1 and one can appeal to the WKBJ approximation de-

scribed in Section 11.2. In this limit we shall draw on illustrations from the physics

of wave propagation in inhomogeneous plasmas. If we picture a wave propagating

in the direction of a density gradient, at some point on the density proﬁle it may

encounter a cut-off or a resonance. As we found in Chapter 6, propagation beyond

a cut-off is not possible and the wave is reﬂected, whereas at a resonance, wave

energy is absorbed. The WKBJ approximation breaks down in the neighbourhood

of both cut-offs and resonances. We shall illustrate some aspects of this physics by

means of a case history of stimulated Raman scattering, progressing from a local

model for which the WKBJ approximation is a valid representation, to a global

picture of the instability which can only be determined numerically.

Absorption of wave energy at a resonance is the basis of an important method of

plasma heating. For example, radiofrequency heating makes a critical contribution

425

426 Aspects of inhomogeneous plasmas

to heating tokamak plasmas and the whole concept of inertial containment fusion

is based on coupling laser energy to the target plasma. In general, radiation has to

propagate to a resonance where it can be absorbed so accessibility is an important

issue in inhomogeneous plasmas. The next stage of the heating process involves

the transfer of electromagnetic energy to the plasma across the resonant region

by means of mode conversion. Mode conversion describes the coupling of waves

which individually satisfy distinct dispersion relations over a range of parameter

space but which are coupled across some region. WKBJ analysis breaks down in

a region of mode conversion. The second case-history we examine deals with the

coupling of a longitudinal mode in the form of a Langmuir wave to a transverse

electromagnetic wave in the presence of a steep density gradient.

In the second limit kL  1. Under these conditions the change in plasma

density is so steep that the inhomogeneity may sometimes be treated as a sharp

boundary and jump boundary conditions applied. However, in other cases the

physics of the boundary layer is important in characterizing the physics overall.

Plasmas close to material boundaries often display sharp spatial variation even if

relatively homogeneous outside these boundary layers. The importance of such

regions was ﬁrst recognized by Langmuir who showed that for plasmas in contact

with a material surface, the interface between plasma and surface takes the form of

a sheath several Debye lengths thick. This comes about on account of the greater

mobility of electrons over ions that allows a negative potential to be established

across the sheath. Most electrons are therefore reﬂected back into the plasma from

the sheath.

11.2 WKBJ model of inhomogeneous plasma

The most widely used model for describing wave characteristics in non-uniform

plasmas is the WKBJ approximation, developed independently by Wentzel,

Kramers, and Brillouin to solve Schr

odinger’s equation for quantum mechanical

barrier penetration. J recognizes the contribution of Jeffreys who had earlier devel-

oped the same approximation, albeit in a different context. The physical appeal of

the WKBJ approximation is intuitive in that it is only a step beyond the familiar

territory of a plane wave solution.

To keep the discussion as simple as possible consider electromagnetic wave

propagation in an isotropic plasma in which the density varies spatially along Oz.

For a linearly polarized transverse wave the electric ﬁeld E (in the Oxy-plane)

satisﬁes

+ k

(z)E = 0 (11.1)