Boyd T.J.M., Sanderson J.J. The Physics of Plasmas

Подождите немного. Документ загружается.

10.2 Non-linear Landau theory 387

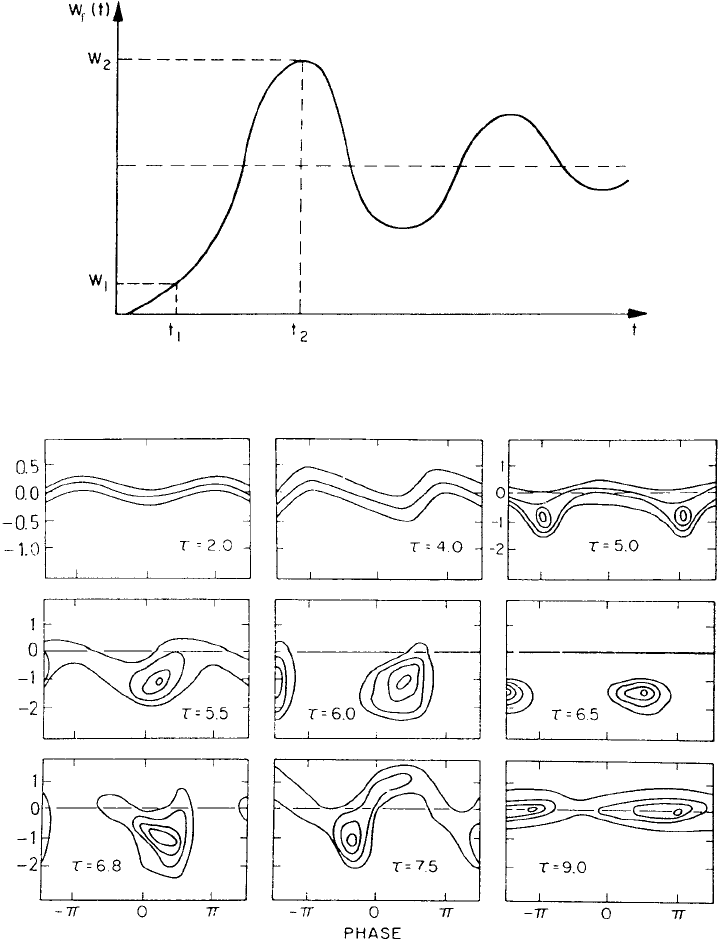
Fig. 10.5. Electrostatic ﬁeld energy as a function of time. The damping time corresponds

to the time characterizing the smearing out of particles in phase space.

Fig. 10.6. Experimental contour plots of the electron distribution in phase space. At τ =

2, 4 the central line represents the maximum electron density contour, the lines on either

side corresponding to the half-maximum value. At later times, the inner contour represents

maximum density. The phase reference is arbitrary and differs for each frame (after Gentle

and Lohr (1973)).

388 Non-linear plasma physics

phase space. Overall the wave energy displays oscillatory behaviour as shown in

Fig. 10.5.

The main predictions of the non-linear phase of BPI were conﬁrmed in ex-

periments by Gentle and Lohr (1973) measuring maximum wave amplitude,

monochromaticity of the unstable mode and its harmonic content. Measured con-

tour plots of the electron distribution in phase space are shown in Fig. 10.6.

10.2.4 Plasma echoes

A quite remarkable prediction of non-linear Landau theory is the existence of what

are called plasma echoes. There is no dissipation in a collisionless plasma and

therefore no increase in entropy. Consequently, although a wave may effectively

disappear as its amplitude decreases through Landau damping, some trace of it

remains in the perturbed distribution function f

. This trace lies in the terms that

we discarded in quasi-linear theory on the grounds that they were transient. Specif-

ically, we noted that, on taking the Laplace transform of (10.8), the ballistic term

varies like exp(−ik · vt) but we dropped it because it becomes highly oscillatory

in k ·v as t →∞and therefore makes a negligible contribution to an integral over

k or v. This is called phase mixing. Note, however, that the ballistic term itself does

not decay; it is this term that carries the information about the initial perturbation

that produced the Landau damped wave.

Now the idea behind the plasma echo is to create two Landau damped waves

at different times t

and t

such that at a later time t

a third wave (the echo) may

arise from their non-linear interaction. At time t the ballistic term from wave 1

with wavenumber k

varies like exp(−ik

· v(t − t

)) and similarly for wave 2 like

exp(−ik

· v(t − t

)). If we now resurrect the second-order terms on the right-hand

side of (10.4), which were neglected in quasi-linear theory, we get contributions

varying like exp(−i[k

· v(t − t

) − k

· v(t − t

)]). Choosing k

and k

to be in

the same direction we see that the exponent vanishes at

t = t

− k

Consequently, when the velocity integral in (10.2) is performed at t = t

there is

no phase mixing and the echo wave appears.

This effect, which can be discussed in spatial terms also, generating the waves

at separate points in a plasma column and observing the echo at a third point

further down the column, has been demonstrated experimentally by Wong and

Baker (1969).

10.3 Wave–wave interactions 389

10.3 Wave–wave interactions

So far our discussion of non-linear effects has been largely by extension of the

Landau theory into the non-linear regime. We began with wave–particle interac-

tions and with the discussion of plasma echoes we have moved on to wave–wave

interactions though, in this case, one which is realized via the resonant particles.

Another example of this kind is induced scattering in which the resonant particles

interact with the beat wave of two plasma waves. It is interesting to note the

sequence of resonance conditions. For linear Landau damping (or growth) we have

ω = k · v

and this was also the resonance condition for particle trapping where only one

wave is involved. The resonance condition for induced scattering is obtained by

substituting the relevant ω and k for the beat wave. When this is between two

plasma waves, denoted by frequencies and wavenumbers, (ω

, k

) and (ω

, k

we have

− ω

= (k

− k

) · v

If the ﬁrst wave is driven with a ﬁnite amplitude the second can arise through the

non-linear interaction with the resonant particles and hence the description of this

process as induced scattering. Since the beat wave frequency for Langmuir wave

scattering is low (ω

,ω

≈ ω

, ω

− ω

 ω

) the scattering is off the ions and

the process is adequately described by ion Landau theory combined with a ﬂuid

description of the electron waves as discussed, for example, in Nicholson (1983).

The next stage in this progression is to consider direct wave–wave interactions.

It is often the case that wave–particle coupling is sufﬁciently weak that it is in-

signiﬁcant and yet plasmas can support so many waves that if one wave (ω

, k

) is

propagating and another natural mode (ω

, k

) spontaneously arises, resonant non-

linear coupling may give rise to the beat wave (ω

, k

). The resonance conditions

for this are

= ω

+ ω

(10.25)

= k

+ k

(10.26)

and the waves are said to form a resonant triad. Of course, we could go on in this

way and have four or more waves in resonance but since this involves cubic or

higher order terms these are less likely to be of signiﬁcance than resonant triads.

Derivation of the equations describing non-linear wave coupling may be via

the Vlasov–Maxwell equations or the two-ﬂuid wave equations and may treat the

waves as coherent or take ensemble averages of systems with many waves having

random phases (weak turbulence analysis); for a thorough discussion of this topic

390 Non-linear plasma physics

see Davidson (1972). Whatever the analysis, the end product is a set of equations

of the general form

∂ A

(k, t)

∂t



dk dk





δ(k −k



− k



αβγ

(k, k



, k



)

×A



, t)A



, t)e

i[ω

(k)−ω



)−ω



)]t

(10.27)

where A

α,β,γ

are the wave amplitudes and K

αβγ

is the interaction kernel for the

triplet (α,β,γ). In fact, equations with this structure arise in many branches of

physics and engineering and it is only the kernel K

αβγ

which varies according

to the speciﬁc non-linear wave coupling under consideration. To avoid a lot of

heavy algebra therefore, we shall derive the equations for a simple system of three

coupled harmonic oscillators. In other words, we model the waves by harmonic

oscillators and the plasma as the medium which supports them and allows their

interaction.

If C is the (constant) coupling coefﬁcient for the three oscillators, the equations

of motion are

¨x

+ ω

=−Cx

¨x

+ ω

=−Cx

¨x

+ ω

=−Cx







(10.28)

In the linear approximation the solutions are



iω

+ A

∗

−iω



( j = 0, 1, 2)

and if the coupling is weak we may expect the non-linear solutions to be of the

form



(t)e

iω

+ A

∗

(t)e

−iω



(10.29)

where the amplitudes A

are now slowly varying functions of t such that



 ω

(10.30)

Substituting (10.29) in (10.28) we get for the ﬁrst member

+ 2iω

) + (

∗

− 2iω

∗

−2iω

=−

iω

+ A

∗

−iω

)(A

iω

+ A

∗

−iω

and, when we average over the fast time scale, phase mixing gets rid of the second

term on the left-hand side and all terms on the right-hand side except the one whose

10.3 Wave–wave interactions 391

exponent vanishes because of the resonance condition (10.25). In view of (10.30)

we may drop the

term as well, leaving

4ω

The corresponding equations for the second and third members of (10.28) are

4ω

∗

and

4ω

∗

It is convenient to re-deﬁne the amplitudes by

= A

1/2

(10.31)

to get the more symmetric set of equations

˙a

= iKa

˙a

= iKa

∗

˙a

= iKa

∗







(10.32)

where

K = C/4(ω

)

1/2

(10.33)

is the common coupling coefﬁcient.

Although the details of the derivation of the equation set (10.32) for the non-

linear wave coupling in a plasma are more complicated, the method is the same.

The condition (10.26) on the wavenumbers, expressed by the delta function in

(10.27), arises because the waves have spatial as well as temporal harmonic varia-

tion, exp i(k ·r −ωt), and is necessary to avoid phase mixing in space.

From (10.25) and (10.32) it is easily shown that



+ ω



= 0 (10.34)



+|A



= 0

which expresses the conservation of energy since wave energy density is propor-

tional to the square of the amplitude.

Directly from (10.32) we get

−

d|a

392 Non-linear plasma physics

−

d|A

(10.35)

which are the Manley–Rowe relations, ﬁrst discussed in the context of parametric

ampliﬁcation in electronics. They show the rates at which energy is transferred

between the waves. An exact solution of (10.32) is obtainable in terms of elliptic

functions showing the periodic nature of the interaction.

Generalizations of the theory may be introduced, the most important of which

is wave damping. This is done by adding a term ν

to the left-hand side of the

equation in (10.32), where ν

is the linear damping rate of the j th wave. As

discussed further below, this introduces a threshold for the spontaneous excitation

of a natural mode since there are now competing effects and the energy in the

excitation must exceed that lost by damping.

Another important generalization is to allow for spatial variation of the wave

amplitudes by replacing the time derivative d/dt by the convective derivative

(∂/∂t +v

·∇), where v

is the group velocity of the j th wave. This means that the

interaction is now between wave packets rather than monochromatic waves, adding

a touch of reality. Other extensions of the theory, which we investigate below, allow

for frequency and wavenumber mismatch.

10.3.1 Parametric instabilities

The interest of plasma physicists in wave–wave interactions has arisen in the con-

text of plasma heating and particularly in the ﬁeld of laser–plasma interactions.

The laser beam is a large amplitude, transverse, electromagnetic wave being driven

through the plasma and is capable, by means of resonant three-wave coupling, of

transferring its energy to two other waves. Such a process in which natural modes

grow at the expense of the large amplitude wave, usually referred to as the pump

wave, is known as a parametric instability.

In this class of three-wave interactions we distinguish between the pump wave

(ω

, k

) and the so-called decay waves which are both small amplitude. Thus, from

(10.32) to ﬁrst order, it follows that a

is constant and we investigate the growth

of a

and a

. To ﬁnd the threshold condition, damping, which may be Landau or

collisional, is included, so the equations are

˙a

+ ν

= iKa

∗

˙a

+ ν

= iKa

∗



(10.36)

where ν

and ν

are both positive. Taking the complex conjugate of the second

10.3 Wave–wave interactions 393

equation in (10.36) and trying a solution ∝ e

αt

we get

(α + ν

− iKa

∗

= 0

iKa

∗

+ (α + ν

= 0

for which there is a non-trivial solution if

(α + ν

)(α + ν

) − K

= 0 (10.37)

Separating real and imaginary parts of this equation we see that α must be real and

has a positive root if

>ν

(10.38)

This is the threshold condition for the instability stating that the combination of

the energy in the pump wave and the strength of the non-linear coupling must be

sufﬁcient to overcome the damping of the decay waves.

Conditions (10.25) and (10.26) represent perfect matching. In practice we need

to explore the consequences of allowing a small frequency mismatch such that

− ω

= ω

where |ω| is very much smaller than any of the wave frequencies. Then instead

of (10.36) we have

˙a

+ ν

= iKa

∗

iωt

˙a

+ ν

= iKa

∗

iωt



(10.39)

where the residual factor e

iωt

is a slow variation like a

(t) and a

(t) andisbest

dealt with by absorbing it into the amplitudes by deﬁning ˜a

= a

−iωt/2

.Now

(10.39) becomes

d ˜a

/dt +

(

iω/2 + ν

)

˜a

= iKa

˜a

∗

d ˜a

/dt +

(

iω/2 + ν

)

˜a

= iKa

˜a

∗



(10.40)

and proceeding as for (10.36) it is easily veriﬁed that the resulting auxiliary equa-

tion replacing (10.37) is

(α + ν

+ i ω/2)(α + ν

− i ω/2) − K

= 0

This equation now has complex roots but at threshold (α = 0), on separating real

and imaginary parts, we ﬁnd

= ν

(ω)

(ν

+ ν

)

(10.41)

showing by comparison with (10.38) the increase in pump wave energy required to

overcome frequency mismatch.

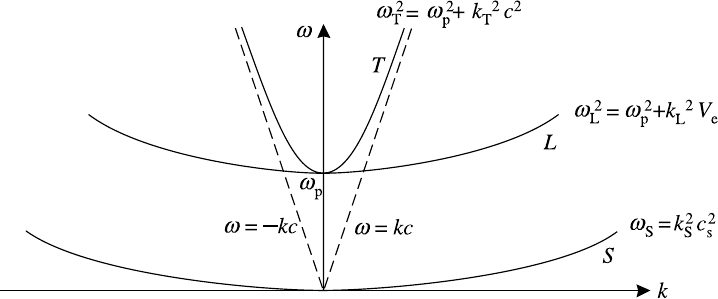
394 Non-linear plasma physics

Fig. 10.7. Dispersion relations for transverse electromagnetic, Langmuir and ion acoustic

waves.

Wavenumber mismatch has a similar effect reducing growth rate and increasing

the threshold for instability. These are important considerations since plasmas,

especially laser-produced plasmas, are highly inhomogeneous so the relationship

between ω and k changes as a dispersive wave travels through the plasma. Con-

sequently, the resonant triad conditions between the pump and decay waves will

be satisﬁed only in some restricted region and the parametric instability is likewise

restricted. These effects are examined in the following chapter. Here we present

a brief qualitative discussion of four parametric instabilities important in laser–

plasma interactions.

We consider an unmagnetized plasma, with T

 T

, irradiated by an intense

laser beam. In this case the three-wave coupling takes place between various com-

binations of the transverse, electromagnetic pump wave for which

= ω

+ k

(10.42)

the longitudinal, electrostatic electron plasma (or Langmuir) wave

= ω

+ k

(10.43)

and the longitudinal, ion acoustic (or sound) wave

= k

(10.44)

These dispersion relations were derived in Chapter 6 and are sketched in Fig.

10.7. We consider only positive frequencies but k values may be of either sign.

The decay waves, labelled 1 and 2, may be any of the pairs

(1, 2) = (L, S), (L

, L

), (T



, S), (T



, L)

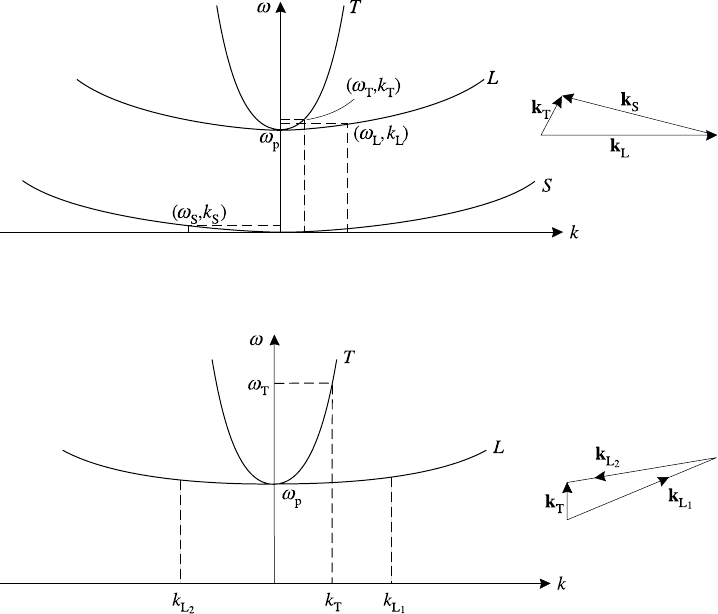
10.3 Wave–wave interactions 395

Fig. 10.8. Frequencies and wavenumbers for parametric decay instability.

Fig. 10.9. Frequencies and wavenumbers for two plasmon decay instability.

where the second possibility has two Langmuir waves and the third and fourth

involve a second (scattered) transverse wave. These are the only three-wave de-

cays allowed in an unmagnetized plasma. Figures 10.8–10.11 illustrate the four

cases.

The parametric decay instability (T → L + S) has ω

≈ ω

since ω

 ω

Also, to avoid strong Landau damping of the Langmuir wave (low threshold) we

need ω

≈ ω

. Thus, the instability occurs near the critical surface (ω

≈ ω

Another consequence of the approximation (ω

≈ ω

) in a non-relativistic plasma

is that |k

||k

| and hence that k

≈−k

. Note that although k

and k

are

almost antiparallel they cannot be exactly so because strong coupling requires the

electric ﬁeld of the transverse wave E

to be closely aligned to k

and k

and so k

must be approximately perpendicular to them. Enhanced energy absorption results

from this instability because the laser energy goes into two plasma waves which

propagate only within the plasma and therefore cannot leave it.

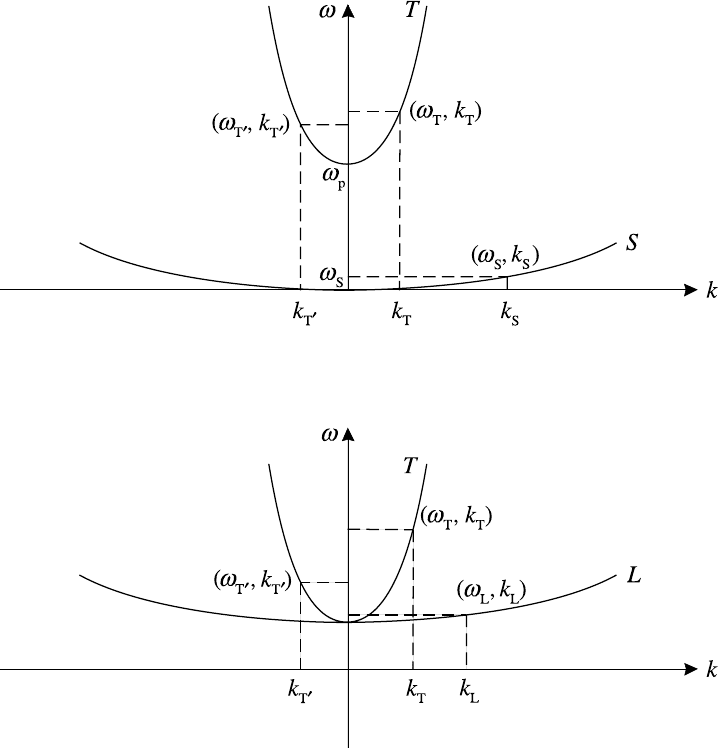
396 Non-linear plasma physics

Fig. 10.10. Frequencies and wavenumbers for stimulated Brillouin scattering.

Fig. 10.11. Frequencies and wavenumbers for stimulated Raman scattering.

For the two plasmon decay instability (T → L

+ L

) the same argument about

avoiding Landau damping for a low threshold means that ω

≈ ω

and

hence ω

≈ 2ω

. It follows that this instability occurs around quarter-critical

density. Here again strong coupling requires k

≈−k

and is maximized

when k

makes angles of approximately π/4 and 5π/4 with k

and k

. En-

hanced energy absorption results for the same reasons as for the parametric decay

instability.

In contrast with the previous cases both of the scattering instabilities may be one

dimensional in the sense that the k vectors can all be collinear. From Fig. 10.10