Boyd T.J.M., Sanderson J.J. The Physics of Plasmas

Подождите немного. Документ загружается.

10.4 Zakharov equations 397

we see that for stimulated Brillouin scattering (T → T



+ S), k



is necessarily

in the opposite direction to k

so that the scattered transverse wave takes energy

back out of the plasma. Furthermore, since ω

 ω

, it follows from (10.35) that

energy from the pump wave goes overwhelmingly into the transverse wave and

not the plasma wave. This instability is therefore very detrimental to laser energy

absorption by the plasma. The wave matching can occur for any frequency ω

>ω

and thus the instability may arise anywhere up to the critical surface.

Stimulated Raman scattering (T → T



+ L) is discussed in more detail in the

next chapter. Since, as before, we require ω

≈ ω

for low threshold and ω



≥ ω

the instability can only occur for ω

≥ 2ω

, i.e. at and below quarter-critical den-

sity. As for Brillouin scattering, the scattered wave travels in the opposite direction

to the incoming wave and therefore takes energy back out of the plasma. In this

case, however, more of the energy gets into the plasma wave.

Quenching of parametric instabilities may come about as a result of:

(i) depletion of the pump wave to below threshold intensity;

(ii) decay of the daughter waves leading to a cascade of modes;

(iii) particle trapping as the electrostatic decay waves achieve large amplitude.

Trapped particles may damp the wave at a rate greater than the linear

damping; this affects the threshold and may switch off the instability;

(iv) plasma inhomogeneity leading to wavenumber mismatch.

10.4 Zakharov equations

In this section we investigate an important example of the modiﬁcation of linear

wave propagation by the retention of non-linear terms in the wave equations. The

coupled equations we shall derive were ﬁrst obtained by Zakharov (1972) using

heuristic arguments to express analytically the physical effects involved in the

coupling.

The problem we wish to study is the interaction of electron plasma and ion

acoustic waves. The ﬁrst is a high frequency wave dominated by the electron

dynamics and the second a low frequency wave dominated by the ion dynamics.

The role of the non-dominant species is to maintain approximate charge neutrality.

The separation of these waves in linear theory is a direct result of the high ion

to electron mass ratio. On the fast time scale of the electron wave the massive

ions are essentially in static equilibrium. For the ion wave, on the other hand, the

electrons are in dynamic equilibrium in the sense that their inertia is so small

that they respond quickly enough to maintain force balance on the slow time

scale. The coupling of ions and electrons via charge neutrality, however, means

that the ion waves produce, through ion density ﬂuctuations, a small perturbation

398 Non-linear plasma physics

of the electron wave dispersion relation. Likewise, the electron waves inﬂuence

the ion waves by the appearance of the ponderomotive force in the force balance

equation.

To ﬁnd the non-linear interaction of these waves we carry out a two-time scale,

perturbation analysis of the warm plasma wave equations given in Table 3.5. The

procedure is similar to that applied to the Vlasov equation to obtain the quasi-linear

equations in Section 10.2.1. There are two time scales because the electrons can

react to the ﬁelds much more rapidly than the massive ions. Electron and ﬁeld

perturbations, therefore, have fast and slow components which we denote by sub-

scripts f and s, respectively; ion perturbations, on the other hand, have only slow

components denoted by subscript 1.

In equilibrium there are no ﬁelds and Zn

= n

, say. Even in the perturbed

state, the rapid response of the electrons to the strong Coulomb force maintains

approximate charge neutrality so that Zn

≈ n

and u

≈ u

. Thus, we have

= n

+ Zn

≈ n

+ n

(10.45)

= n

+ n

(10.46)

= u

≈ u

(10.47)

= u

+ u

(10.48)

Note that the fast time scale perturbations have time dependence of the form

a(t)e

−iωt

where the amplitude a(t) is slowly varying compared with the ﬂuctu-

ations at frequency ω, that is



 ω (10.49)

so that when averaging over the fast time scale the amplitude may be treated as

constant and we have

n

=n

+ n

u

=u



(10.50)

These equations deﬁne the slow perturbations and then (10.46) and (10.48) deﬁne

the fast perturbations as

= n

−n



= u

−u





(10.51)

From

q = e(Zn

− n

)

10.4 Zakharov equations 399

it follows that

= e(Zn

− n

) = 

∇ · E

(10.52)

=−en

= ε

∇ · E

(10.53)

where the total ﬁeld

E = E

+ E

(10.54)

Assuming ions and electrons behave like perfect gases and eliminating the partial

pressures using the adiabatic gas equation, the warm plasma wave equations are

∂n

∂t

+ ∇(n

) = 0 (10.55)



∂

∂t

+ u

· ∇



−

∇n

(10.56)

For the electrons these equations contain non-linear terms n

and u

· ∇u

for

which we need to calculate fast and slow components and we do this using the

same recipe used for the linear terms (10.50) and (10.51). Thus,

)

=n

=(n

+ n

)(u

+ u

)

= (n

+ n

+n

 (10.57)

)

= n

−n



= (n

+ n

+ (n

−n

) (10.58)

and

· ∇u

)

=(u

+ u

) · ∇(u

+ u

)

= u

· ∇u

+u

· ∇u

 (10.59)

· ∇u

)

= u

· ∇u

+ u

· ∇u

+ (u

· ∇u

−u

· ∇u

) (10.60)

We shall not keep all of the non-linear terms in (10.57)–(10.60) but only those

of ‘leading order’. To determine which are leading order terms we assume that

||n

| and |u

||u

|. The ﬁrst of these assumptions is justiﬁed on the

grounds that n

is limited by charge neutrality whereas n

, since it is matched by

, is not. The second assumption is obvious since u

≈ u

, the ion ﬂow velocity.

Note also that the pressure term in (10.56) is treated as a linear term since we shall

replace n

in the denominator by its equilibrium value.

400 Non-linear plasma physics

With these preliminaries we now proceed to the fast wave analysis for which the

relevant equations are (10.53) and, from (10.55) and (10.56),

∂n

∂t

+ ∇ ·



+ n



= 0 (10.61)

∂u

∂t

=−

−

∇n

(10.62)

In fact, the only non-linear term retained is the leading order term in (10.58), all

the non-linear terms in (10.60) being negligible compared with ∂u

/∂t in (10.62).

Next, we take the partial time derivative of (10.61), neglect the slow ∂n

/∂t term

and substitute for n

from (10.53) and for ∂u

/∂t from (10.62) to get

∇ ·



∂

∂t

+ (n

+ n

)



−

∇(∇ · E

)



= 0

Hence, assuming all perturbations are vanishingly small initially,

∂

∂t

+ ω

−

∇(∇ · E

) =−ω





(10.63)

where the (n

) contribution to the pressure term has been dropped.

If, for the moment, we neglect the non-linear term on the right-hand side of

(10.63) and assume E

∼ exp i(k · r − ωt), we recover the dispersion relation

(6.95) for electron plasma waves

= ω

+ k

= ω

(1 + γ

)

Thus, (10.63) is the equation for the non-linear development of these waves when

they interact with the slow waves through the slow time scale perturbation in the

electron density. Since electron plasma waves are strongly Landau damped unless

k  k

we may take the fast frequency to be approximately ω

and write

(r, t) = E

(r, t)e

−iω

(10.64)

Substituting (10.64) in (10.63) and neglecting the term in ∂

/∂t

gives

2iω

∂E

∂t

∇(∇ · E

) = ω





(10.65)

This equation for the evolution of the amplitude of the fast wave is the ﬁrst Za-

kharov equation. To it we must add an equation for the evolution of n

This comes from (10.55) and (10.56) for the ions which are to leading order

∂n

∂t

+ n

∇ · u

= 0 (10.66)

∂u

∂t

−

Zγ

∇n

(10.67)

10.4 Zakharov equations 401

and the slow time scale equation of force balance for the electrons. In this we

must include the ponderomotive force which was derived in Section 2.14 and

takes account of electron acceleration due to the slow variation in amplitude of

the electric ﬁeld. Thus, from (2.68) and (10.56) we have

∇n





∇|E

= 0 (10.68)

In the ion equations we replace u

by u

, Zn

by n

, and substitute for E

from

(10.68) to get

∂u

∂t

=−





∇|E

−

∇n

(10.69)

where c

[

(γ

+ γ

)/m

]

1/2

is the ion acoustic speed. Now taking the

partial time derivative of (10.66) and substituting for ∂u

/∂t from (10.69) gives



∂

∂t

− c

∇



∇

(10.70)

which is the second Zakharov equation and, together with (10.65), gives a closed,

coupled pair of equations for E

and n

To understand the physics of this non-linear analysis let us brieﬂy review the

essential steps. We have reduced two sets of equations (10.53), (10.61), (10.62)

and (10.66)–(10.68) to a pair of coupled equations (10.65) and (10.70). We have

retained only one non-linear term in each of these sets, ∇ · (n

) in (10.61) and

the ponderomotive term in (10.68). Without these non-linear terms we recover the

uncoupled linear wave equations for electron plasma waves and ion acoustic waves.

The non-linear coupling takes account of the maintenance of approximate charge

neutrality so that the slow perturbation in ion density must have a matching slow

perturbation in electron density n

≈ Zn

. This appears as a ‘correction’ to the

electron plasma frequency in (10.63) and subsequently as a moderating term in the

evolution equation (10.65) for the wave amplitude.

Similarly, in the slow wave equations we have allowed for the moderation of E

caused by the displacement of electrons due to the ponderomotive force. Linear

theory says that the dynamic equilibrium of the electrons is maintained by the

balance of the electrostatic ﬁeld and electron pressure gradient; non-linear theory

recognizes that there are three forces in balance. Consequently, the ponderomo-

tive term appears in the evolution equation (10.70) for the slow density perturba-

tion.

As noted in Section 2.14, the effect of the ponderomotive force is to drive elec-

trons away from regions of high wave intensity. For the case where the gradient

in ﬁeld amplitude is parallel to the ﬁeld this is easily explained with the help of

402 Non-linear plasma physics

Fig. 10.12. Electron motion in inhomogeneous, oscillating electric ﬁeld.

Fig. 10.12 which shows successive half-cycles of the electron motion in a ﬁeld

with amplitude increasing to the right; the dashed line represents the mid-point of

the electron oscillations. In the half-cycle when the force −eE is to the right the

electron experiences a weaker force than in the next half-cycle when the force is to

the left. Consequently, the net effect is to cause the electron to migrate to the left,

i.e. in the direction of the weaker ﬁeld. The result is the same when the gradient in

amplitude is perpendicular to the ﬁeld but in this case the ponderomotive acceler-

ation arises from the v × B ∼ v × ∇ × E

term. In both cases the acceleration is

given by (2.68). The migrating electrons drag the ions with them creating plasma

cavities in regions of high ﬁeld intensity and leading to a new kind of instability,

known as the modulational instability.

10.4.1 Modulational instability

Following Nicholson (1983), we may write the one-dimensional Zakharov equa-

tions in terms of dimensionless variables (see Exercise 10.7) as

∂ E

∂τ

∂

∂z

= nE (10.71)

∂

∂τ

−

∂

∂z

∂

|E|

∂z

(10.72)

where E and n are proportional to |E

| and n

, respectively, and τ and z are the

dimensionless time and space variables.

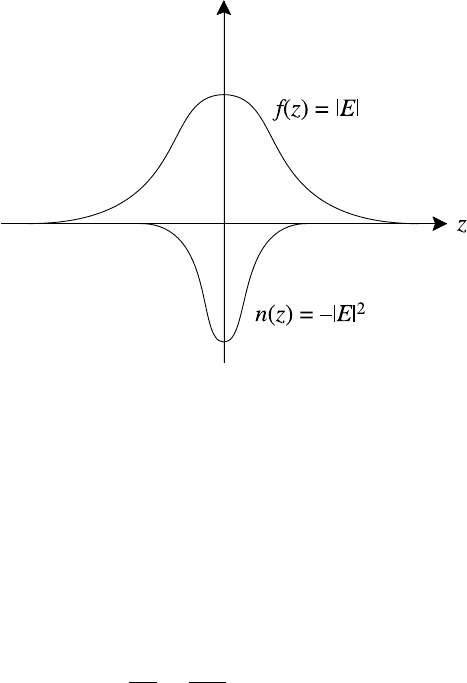
10.4 Zakharov equations 403

Fig. 10.13. Density depletion induced by ﬁeld ampliﬁcation.

Seeking a stationary solution of (10.72) we drop the ﬁrst term and integrate twice

with respect to z to obtain

n =−|E|

(10.73)

where constants of integration have been set equal to zero. Substitution in (10.71)

then gives the non-linear Schr

odinger equation

∂ E

∂τ

∂

∂z

+|E|

E = 0 (10.74)

Such equations occur in different contexts throughout physics and it is well-known

that they have constant proﬁle, single wave solutions known as solitary waves or

solitons. For example, seeking a solution of the form

E(z, t) = e

iτ

f (z)

we ﬁnd

f (z) = (2)

1/2

sech(

1/2

This is sketched in Fig. 10.13 which also shows

n(z) =−2sech

(

1/2

and demonstrates the effect of ﬁeld concentration and density depletion that we

have been discussing. Such density depletions are often referred to as cavitons.

404 Non-linear plasma physics

Fig. 10.14. Illustration of (a) modulation and (b) ﬁlamentation of wave due to the pon-

deromotive force.

Although we have found only the very simplest solution of (10.71)–(10.72),

in which the wave oscillates within the static envelope f (z), it is easy to see

how the ponderomotive force leads to an instability. Consider the propagation of

a constant amplitude wave through an almost homogeneous plasma. Any small

density depletion will be matched by a corresponding amplitude increase. The

ponderomotive force will then deﬂect plasma from this region of increased wave

intensity thereby augmenting the density depletion. This is called the modulational

instability when it refers to the modulation of wave envelope along the direc-

tion of propagation as shown in Fig. 10.14(a). Modulation of the wave proﬁle

can continue to a stage where the wave energy is conﬁned to localized cavitons

several Debye lengths in dimension. This is known as Langmuir collapse. The

10.5 Collisionless shocks 405

collapse in coordinate space is accompanied by so-called pumping in k space,

with increasing k compensating for decreasing density in the dispersion relation

= ω

+ 3k

Although our analysis has involved only longitudinal waves, the ponderomotive

effect applies equally to electromagnetic waves and can produce ﬁlamentation of

the wave. This refers to the break-up of the wave in the direction transverse to

its propagation and is illustrated in Fig. 10.14(b). It is most easily understood in

terms of the refraction of the electromagnetic wave. In an inhomogeneous plasma

decreasing density means increasing refractive index and consequent focusing of

electromagnetic waves. The ponderomotive force then reinforces this effect by

driving plasma away from the region of increased wave intensity. In this way an

initially uniform beam can break up into narrow ﬁlaments. This is an important ef-

fect in laser plasma physics since it can obviously be triggered by non-uniformities

in the laser beam.

10.5 Collisionless shocks

The MHD shocks discussed in Section 5.6 have widths of the order of a mean free

path since collisions are responsible for the sudden change of state. In plasmas,

however, shock-like changes of state are found to occur over distances much less

than the mean free path. Perhaps the clearest example of this is the Earth’s bow

shock created by the interaction of the solar wind with the Earth’s magnetic ﬁeld

to produce the transition from supersonic ﬂow in the solar wind to sub-sonic ﬂow

in the magnetosheath. The shock has a thickness of about 1000 km whereas the

collisional mean free path is of the order of 1 AU or 10

km. Clearly, collisions

cannot be responsible for this change of state. Other examples arise in laboratory

plasmas where changes of state occur within a few mean free paths but collisional

transport is insufﬁcient to account for this and so-called turbulent or anomalous

dissipation must be involved. Any shock in which non-collisional processes play a

signiﬁcant role is called a collisionless shock.

The ﬁrst important difference to note between collisional and collisionless

shocks relates to the formation of the shock. In collisional shocks the wave proﬁle

results from the balance between convective and dissipative effects. The wave

proﬁle in collisionless shocks, on the other hand, is usually the result of a balance

between convective and dispersive effects. To understand how this comes about

it is useful to consider the wave in terms of its Fourier components. In the linear

approximation each component propagates independently and in the absence of

dispersion a wave pulse will maintain a constant proﬁle since all components travel

with the same speed ω/k. In the non-linear approximation, however, the wave pulse

broadens since any pair of components (ω

, k

) and (ω

, k

) within the pulse, for

406 Non-linear plasma physics

Fig. 10.15. Non-linear broadening and steepening of a wave pulse.

Fig. 10.16. Typical plasma dispersion curves.

which ω = ω

± ω

and k = k

± k

, will be resonantly driven, leading to both

longer and shorter wavelength modes. If, in addition, the wave pulse is regarded as

a combination of compression and expansion waves, the effect of convection is to

steepen the compression wave (the wave-front) and broaden the expansion wave so

that the pulse changes its shape as illustrated in Fig. 10.15. In a collisional shock

wave steepening continues until the wave-front has a sufﬁciently large gradient that

dissipation balances convection.

Plasmas, however, are dispersive and a simple dispersion relation of the form

ω/k = const. will, in general, apply only over a limited band of wavenumbers.

Typical dispersion curves are shown in Fig. 10.16. Starting with a wave pulse

centred around some arbitrary point (ω

, k

) on the straight portion of the curve,

higher wavenumber modes may be generated by non-linear coupling up to the point

(ω

, k

), where the phase velocity changes, i.e. dispersion begins. Resonant mode

generation beyond this point would lead to shorter wavelength modes correspond-