Boyd T.J.M., Sanderson J.J. The Physics of Plasmas

Подождите немного. Документ загружается.

10.2 Non-linear Landau theory 377

In each case, whether the non-linear saturation of instabilities or the growth of

parametric waves, there are two distinct time scales, that of the rapid oscillation of

the initial, linear waves and that of the development of non-linear effects. We shall

see that this is crucial to the construction of an analytic non-linear theory. In those

cases where linear instability, with growth rate γ

, leads on to non-linear effects,

these develop at a rate γ

 γ

. Typically, γ

∼ (W/nk

T )γ

, where W is the

energy density associated with the unstable mode.

Computer simulations play an indispensible role in the study of non-linear

plasma physics. Since the complexities of non-linear equations severely limit the

scope for analytical progress, the usual procedure is to isolate as far as possible the

particular non-linear phenomenon one wishes to investigate by suppressing effects

which complicate the analysis but do not contribute signiﬁcantly to the dominant

non-linear behaviour. In the main this can be done by averaging over the fast time

scale but occasionally it also involves identifying the dominant non-linear term

and dropping all others. Progress can sometimes be made by resorting to model

equations. Parametric ampliﬁcation is one example where this has been done to

good effect, the model equations serving for an entire class of problems in different

branches of physical science.

Our approach in this chapter, therefore, is mainly illustrative. Various non-linear

processes are discussed on the basis of the simplest credible mathematical model

capable of representing the essential physics of the process.

10.2 Non-linear Landau theory

Linear theories are based on the assumption that perturbations of a steady state

or equilibrium are inﬁnitesimally small so that all but the linear terms may be

ignored. In practice, of course, all perturbations have ﬁnite amplitude, however

small, and one may begin a non-linear investigation by asking what would be the

consequences of recognising this. Assuming small, but ﬁnite, perturbations and

keeping quadratric terms in a perturbation expansion is the basis of weakly non-

linear analysis and, for the most part, this will be our approach to the discussion

of non-linear plasma phenomena. Various linear theories will be extended in this

way into the non-linear regime and we begin with Landau’s solution of the Vlasov

equation.

10.2.1 Quasi-linear theory

As its name suggests, quasi-linear theory is a kind of halfway stage between linear

and non-linear theory and was ﬁrst developed to deal with the problem which we

met when discussing the Landau solution of the Vlasov equation. What happens

378 Non-linear plasma physics

if some waves experience Landau growth rather than damping? Obviously, wave

amplitudes cannot grow indeﬁnitely since the total energy is limited. How then is

the growth curtailed? As energy is transferred from particles to waves the distri-

bution of particle velocities must be modiﬁed in some way by this growth in wave

amplitude. It is just this modiﬁcation of the distribution function that we seek to

describe by quasi-linear theory.

We illustrate this approach by means of the simplest possible problem of unsta-

ble, electrostatic waves in an unmagnetized plasma in which we treat the ions as a

uniform neutralizing background. We assume that the velocity space modiﬁcation

of the electron distribution function f (r, v, t) takes place on a much slower time

scale than the ﬂuctuations of the growing waves so that we may separate f into

two parts, a slowly varying f

which is the value of f when averaged over the

ﬂuctuations, and a rapidly varying f

. For simplicity, we assume also that f

spatially uniform so that

f (r, v, t) = f

(v, t) + f

(r, v, t)

The Vlasov equation then reads

∂ f

∂t

∂ f

∂t

+ v ·

∂ f

∂r

−

E ·

∂ f

∂v

−

E ·

∂ f

∂v

= 0 (10.1)

and Poisson’s equation becomes

∇ · E =−



dv (10.2)

the electron charge arising from the slowly varying f

being neutralized by the ion

charge.

Averaging (10.1) over the rapid ﬂuctuations gives

∂ f

∂t



E ·

∂ f

∂v



(10.3)

where X  denotes the average value of X ; all other terms are linear in f

and

therefore have zero averages. This is the equation describing the slow evolution of

. Now subtracting (10.3) from (10.1) we ﬁnd

∂ f

∂t

+ v ·

∂ f

∂r

−

E ·

∂ f

∂v



E ·

∂ f

∂v

−



E ·

∂ f

∂v



(10.4)

which describes the rapid variation of f

. If saturation of the instability takes place

in such a way that f

remains small compared with f

we might plausibly argue

that in these equations only the non-linear term on the right-hand side of (10.3)

need be kept since this determines the rate of change of f

whilst those on the

right-hand side of (10.4) may be neglected compared with the linear terms on the

10.2 Non-linear Landau theory 379

left-hand side. It is in this sense that the theory is quasi-linear; (10.4) is linearized

but not (10.3). Thus, we replace (10.4) by

∂ f

∂t

+ v ·

∂ f

∂r

−

E ·

∂ f

∂v

= 0 (10.5)

This is very like the linearized Vlasov equation (7.16), but not quite the same

because here f

is time-dependent. However, since the rate of change of f

is slow

compared with f

we may treat f

as constant in solving the coupled equations

(10.2) and (10.5) and apply the results of Section 7.3.

The Fourier transform of the electric ﬁeld E(k, t) is given by (7.28) where R

the residue of the pole at p = p

in the integral (7.26). For simplicity, we assume

that there is only one solution of the dispersion relation (7.27) which gives rise to

a pole with p > 0 and that this occurs at

p =−i ω =−iω

=−iω

+ γ

Then all other terms in (7.28) are transient and may be dropped. Evaluating the

residue using L’H

opital’s rule we ﬁnd

E(k, t) =

iee

−iω

(∂(k, ω)/∂ω)



(k, v, 0)

(ω

− k · v)

dv (10.6)

where, since it is more convenient to work in terms of vector variables, we have

replaced E and u using E = Ek/k and ku = k · v. Also, using the transformation

p →−iω =−iω

we have expressed the Laplace transform of the plasma

dielectric function D(k, p) in terms of its Fourier transform

(k,ω

) = 1 +



k · ∂ f

/∂v

(ω

− k · v)

dv = 0 (10.7)

which determines ω

(k, t).

We did not display f

explicitly in Section 7.3 but it is obtained from (7.22) as

(k, v, p) =

p + ik · v



eE(k, p)

∂ f

∂v

+ f

(k, v, 0)



(10.8)

Inverting the Laplace transform then gives contributions from the pole at p =

−ik ·v as well as that at p =−iω

. However, the former varies like exp(−ik ·vt)

and as t →∞it becomes highly oscillatory in k and v space. This term is called

the ballistic term and we shall return to it later. For the moment we note that since

the inverse Fourier transform involves an integral over k its contribution vanishes

as t →∞and so we drop it. Here again, therefore, we keep only the term arising

from the pole at p =−i ω

with the result

(k, v, t) =

ieE(k, t)

m(ω

− k · v)

∂ f

∂v

(10.9)

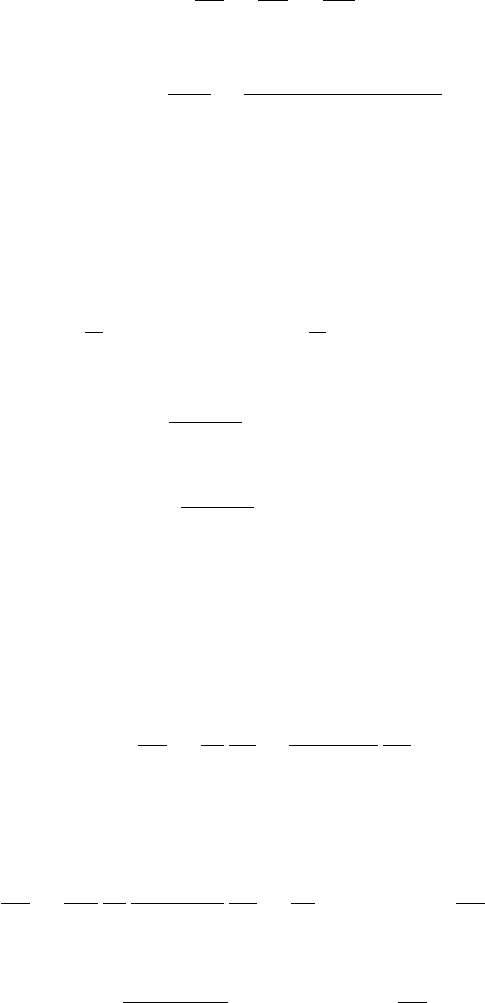
380 Non-linear plasma physics

Substitution of (10.6) and (10.9) in (10.3) then gives the evolution equation for f

in the form of a diffusion equation

∂ f

∂t

∂

∂V

∂ f

∂v

(10.10)

where



dkE

(−k, t)E

(k, t)

(ω

− k · v)

(10.11)

is the diffusion coefﬁcient and V is the volume of the plasma. In deriving (10.10)

we have taken the spatial average of the right-hand side since the left-hand side is

assumed independent of r. Also, although ω

is time-dependent it is only slowly

varying as a function of f

and so has been taken outside the time average over the

rapid ﬂuctuations.

Deﬁning the spectral energy density of the electrostatic ﬁeld by

E(k, t) =

E(−k, t) · E(k, t)=

E

∗

(k, t) · E(k, t) (10.12)

and noting that

∂E(k, t)

∂t

=−iω

E(k, t)

it follows that

∂E (k, t)

∂t

= 2γ E (k, t) (10.13)

Thus, the coupled equations of quasi-linear theory are (10.10), (10.13) and (10.6).

From (10.13) we see that for γ(k, t)>0 the wave amplitude grows thereby

increasing the diffusion coefﬁcient which in turn decreases the slope of f

and

thus reduces γ .

This may be illustrated for the one-dimensional ‘bump-on-tail’ plasma distribu-

tion. In this case (10.10) is

∂ f

∂t

∂

∂v



dkE (k, t)

(ω

− kv)

∂ f

∂v

In the limit γ → 0 we may evaluate the integral over k in the same way as the

integral over u was evaluated in Section 7.3. The principal part vanishes since it is

odd in k and iπ times the residue at the pole gives

∂ f

∂t

πe

∂

∂v

E(ω

/v, t)

∂ f

∂v

∂

∂v

A(v)E (ω

/v, t)

∂ f

∂v

(10.14)

where A(v) = (π e

v). Also since γ ∝ ∂ f

/∂v we may write (10.13) as

∂E (ω

/v, t)

∂t

= B(v)E (ω

/v, t)

∂ f

∂v

(10.15)

10.2 Non-linear Landau theory 381

Fig. 10.1. Illustration of quasi-linear evolution of f

for the bump-on-tail instability.

where A and B are both positive. Combining (10.14) and (10.15) we have

∂ f

∂t

∂

∂v



∂E

∂t



i.e.

∂

∂t



−

∂

∂v





= 0

Then if E is negligible at t = 0

∂

∂v





= f

(v, 0) − f

(v, t)

We seek asymptotically steady state solutions, that is ∂E /∂t, ∂ f

/∂t → 0as

t →∞.If∂E/∂t = 0, from (10.15) either E = 0or∂ f

/∂v = 0. Suppose

∂ f

/∂v = 0 for v

<v<v

and E = 0 for all other v. Then for v

<v<v

(v, ∞) is constant and for all other v, f

(v, ∞) = f

(v, 0). These results are

shown schematically in Fig. 10.1. The unstable region is initially deﬁned by the

range of v for which f



> 0 but as the diffusion progresses this region expands

since f



decreases within the unstable range but becomes positive just outside it.

The instability is quenched when f

is constant across the ﬁnal range of the wave

spectrum between v

and v

. The increase in energy in the waves is compensated

for by the net loss of energy of the particles; faster particles in the initial bump have

been replaced by slower particles ﬁlling the initial trough.

382 Non-linear plasma physics

Quasi-linear theory has been widely used with some success despite the arbi-

trariness of its assumptions and some lack of consensus on the conditions for its

validity.

10.2.2 Particle trapping

Another important wave–particle effect that leads to the quenching of instabilities

is particle trapping. It comes about because waves have ﬁnite amplitudes and

particles with insufﬁcient energy to surmount the wave peaks oscillate back and

forth in the wave troughs.

To investigate this we consider a single wave and assume that its amplitude

grows or decays very slowly compared with the rate at which the wave oscillates.

Then, in a frame of reference moving with the wave speed ω/k, the particles see a

constant wave proﬁle which is a function of x only. The equation of motion of an

electron is

m ¨x =−eE(x) = e

dφ(x)

(10.16)

where φ(x) is the electrostatic potential. A ﬁrst integral is the energy equation

m ˙x

− eφ(x) = E

where E

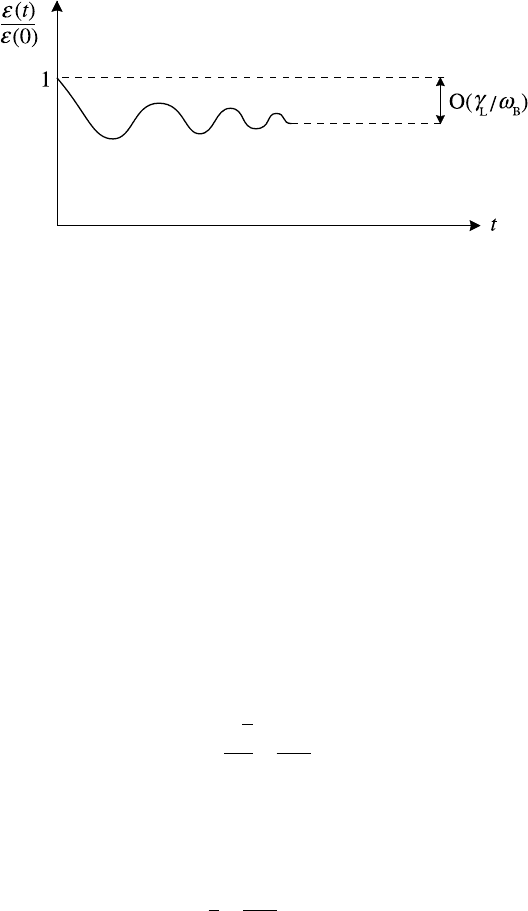
is a constant equal to the total energy of the electron. Clearly, if

> −eφ(x) for all x the kinetic energy is positive for all x and the electron

is untrapped. On the other hand, all electrons with values of E

below the wave

peaks are trapped and oscillate in the wave troughs between the points at which

=−eφ(x). The energy diagram and the phase space trajectories are shown in

Fig. 10.2; in the laboratory frame the trajectories move to the right with the wave

speed ω/k. Note that it is the resonant electrons, those with v ≈ ω/k, that are

trapped.

Electron trapping imposes a severe restriction on the validity of linear Landau

damping theory which, as we saw in Chapter 7, is equivalent to integration over

unperturbed orbits, namely the straight line trajectories: x(t) = x(0) + v(0)t.

The trajectories of the trapped (resonant) electrons have a superimposed oscillatory

motion governed by (10.16) and if E(x) =

E sin kx 

Ekx for the most strongly

trapped electrons (near the bottom of the potential well) we have

m ¨x =−mω

x =−e

Ekx

giving ω

= e

Ek/m ≡ ω

, where ω

is called the bounce frequency. Usually

 ω

but the Landau damping decrement, given by (7.37) and denoted here

10.2 Non-linear Landau theory 383

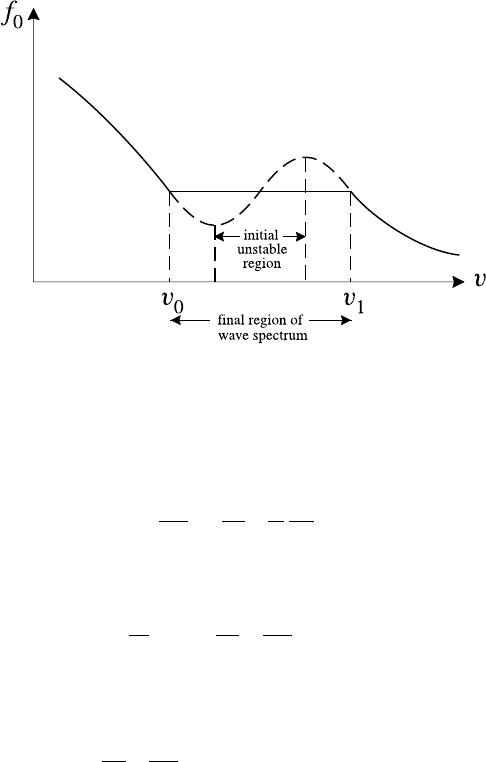
Fig. 10.2. Illustration of particle trapping by ﬁnite amplitude waves. The upper ﬁgure

shows the phase space trajectories and the lower ﬁgure the energy diagram.

by γ

, decreases exponentially for long wavelength plasma oscillations. Clearly, if

>γ

the effect of electron trapping will come into play before appreciable lin-

ear Landau damping takes place. This produces, as discussed by Davidson (1972),

a non-monotonic decay which is shown schematically in Fig. 10.3. The wave

energy decays according to linear Landau theory for t < 2π/ω

, releasing some of

the trapped particles, and then oscillates with a frequency of the order of ω

. This

oscillation frequency increases with t and for t  2π/ω

the wave energy tends to

a constant value which is lower by a fraction of order γ

/ω

times its initial value.

The trapped electrons, by continually exchanging energy with the wave, keep it

from collapsing and produce the oscillations in the wave energy. This damping

is clearly a non-linear process and, although physically quite distinct from linear

Landau damping, is often referred to as non-linear Landau damping.

384 Non-linear plasma physics

Fig. 10.3. Illustration of non-linear Landau damping. If ω

>γ

electron trapping occurs

before the wave has decayed signiﬁcantly and the fractional loss of wave energy is limited

to O(γ

/ω

The theory is equally applicable to the case of growing waves. In this case there

is linear Landau growth followed by oscillation and asymptotic approach to a wave

energy which is a fraction of order γ

/ω

higher than its initial value.

10.2.3 Particle trapping in the beam–plasma instability

We turn next to a consideration of the non-linear phase of the beam–plasma insta-

bility (BPI) analysed in its linear phase for the weak-beam case in Section 6.5.2.

This showed that three of the four solutions to the linear dispersion relation are of

the same magnitude for kv

/ω

 1. The maximum linear growth rate (6.121) is

max

√



2ω



1/3

(10.17)

and the frequency of the growing perturbations is

ω = ω





1 −



2ω



1/3





≡ ω

(1 − δ) (10.18)

Restricting ourselves to the weak-beam limit makes possible a quasi-linear exten-

sion to the linear result (Drummond et al. (1970), O’Neil et al. (1971), Gentle and

Lohr (1973)). As in the linear model we consider only electron dynamics but now

we need to bear in mind that doing so will in general impose restrictions on the

validity of the non-linear result.

10.2 Non-linear Landau theory 385

In the linear regime it is straightforward to show that zero- and ﬁrst-order vari-

ables are related by

=−

which establishes the ordering











(10.19)

Thus, even if the beam density perturbation is not itself small, the changes in both

beam and plasma electron velocities are smaller in order than the beam density

perturbation. We saw in Section 6.5.2 that the BPI spectrum was relatively narrow

so that we may approximate the wave potential φ

by a monochromatic sinusoidal

wave form,

(x, t) = φ

cos ω



− (1 − δ)t



(10.20)

even in the non-linear phase, at least until the stage at which signiﬁcant numbers

of beam electrons are trapped by the wave. In the wave frame ω/k = v

(1 − δ),

the beam electrons experience the potential φ

φ cos kx, where

φ is the time-

averaged amplitude. The trajectory of a test electron (labelled j ) in this potential is

determined by energy conservation from

− e

φ cos kx

= c

(10.21)

An electron for which c

=−e

φ is trapped at the bottom of the potential well

whereas one for which c

= e

φ is on the border between trapped and free electrons.

The critical escape velocity is v

= (4e

φ/m)

1/2

. Thus in the quasi-linear model

some beam electrons will become trapped once the potential has grown to a level

such that v = v

− ω/k = δv

= v

. Then

(v)

(10.22)

with corresponding energy density at time t = t

,say

W (t

) =

 2

−31/3





1/3





(10.23)

Note that this is a small fraction of the beam kinetic energy density. Growth of

the wave continues until most of the beam electrons have been trapped. By this

stage, at t = t

, the beam electrons have lost kinetic energy

m[(v

+ v)

−

− v)

] ∼ 2n

v. Since (10.19) guarantees that the plasma electron

dynamics is still essentially linear, to a good approximation we may assign one

386 Non-linear plasma physics

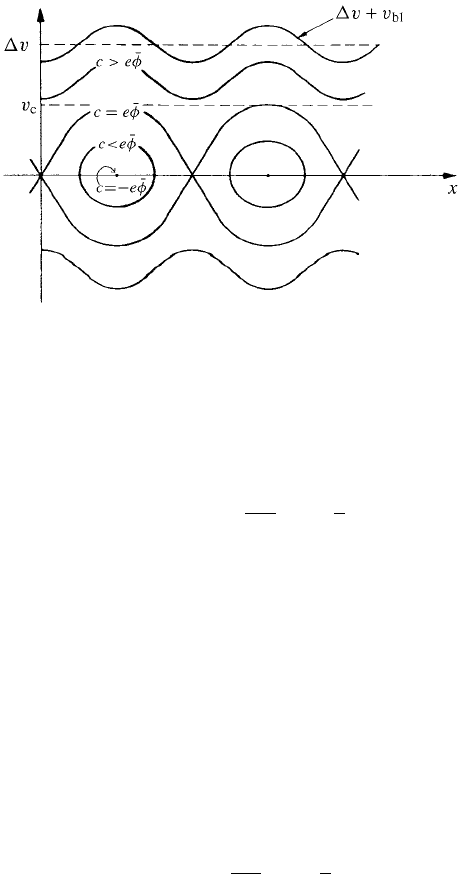
Fig. 10.4. Electron phase space showing trapped and free electron trajectories.

half of the kinetic energy lost to the oscillations and the other half to electrostatic

ﬁeld energy. Then at time t = t

the average ﬁeld energy density is

W (t

)  n

v = 2

−1/3





1/3





(10.24)

Comparing (10.23) with (10.24) we see that W (t

) = 2

W (t

). Note that for

= 0.015, only 20% of beam kinetic energy is converted to ﬁeld energy.

As particle velocities bounce back up, ﬁeld energy is reconverted into kinetic

energy but since the potential well is not parabolic, particles oscillate at different

frequencies. In the phase space representation in Fig. 10.4 electrons rotate round

equipotential contours and undergo phase mixing with the result that the position

of the beam electrons in phase space is smeared out after some rotations. The ﬁeld

oscillations die out and the ﬁeld energy settles at a value that is half the difference

between the initial beam energy and that of the smeared-out distribution, i.e.

(t  t

) = 2

−4/3





1/3





as illustrated in Fig. 10.5.

This simple picture does not provide an accurate representation of beam dy-

namics. Figure 10.4 illustrates the velocity modulation of the beam so that even

when v

= v trapping is not complete. One can show that when trapping occurs

the beam velocity modulation v

= v which in turn implies that n

= 1;

in other words the beam electron dynamics is seriously non-linear, with bunch-

ing well developed. The bunches are trapped in the potential well and rotate in