Boyd T.J.M., Sanderson J.J. The Physics of Plasmas
Подождите немного. Документ загружается.


9.7 Scattering of radiation by plasmas 357
the incident frequency) and along the direction of propagation of the scattered wave
(up-shifting the frequency).
The next step is determining the scattered power. Making use of the property of
the delta function expressed in Exercise 9.1 we may invert (9.85) to get
E
s
(r, t) =
r
e
r
P · E
0
e
i(k
s
·r−ω
D
t)
(9.87)
The corresponding Poynting flux is
S
s
=
1
2
cε
0
r
e
r
2
|P · E
0
|
2
n
The power per unit solid angle per unit frequency in the scattered radiation is then
d
2
P
d dω
s
= r
2
e
S
0
|P · e|
2
δ(ω
s
− ω
D
) (9.88)
where S
0
is the mean incident Poynting flux and e = E
0
/|E
0
|.
Provided correlations between plasma electrons and ions are unimportant the to-
tal scattered power is found by adding the contributions from individual electrons.
We shall see in Section 9.8 that this is permissible provided kλ
D
1. For present
purposes it is enough to note that for kλ
D
1, the phase difference between the
radiation fields from a test electron and from electrons in its Debye cloud is large
and in consequence the radiation fields of the test electron and its Debye cloud are
incoherent. Under these conditions the total scattered power is found by averaging
(9.88) over the electron distribution.
At this point we need to exercise some care. In computing the total power
in the radiation scattered by electrons in some volume element dr we add the
contributions from individual electrons which means that we must measure time
at the source, not at the detector. As we have already seen in Section 9.2.2 this
has the effect of introducing a factor dt/dt
≡ g. Sheffield (1975) has given an
instructive physical argument for this finite transit time effect, the need for which
was identified by Pechacek and Trivelpiece (1967). The scattered power from a
distribution of electrons f (v) in a scattering volume V is then
d
2
P
d dω
s
= r
2
e
V
S
0
|P · e|
2
f (v)g
2
δ(ω − k · v)dr dv (9.89)
showing both g factors, one from (9.85), the other from the transit time effect.
In the non-relativistic limit these distinctions disappear and (9.89) is greatly
simplified by discarding g
2
and taking the polarization dyadic out of the integrand
since it is velocity-independent in this limit. Then (9.89) reduces to
d
2
P
d dω
s
=
r
2
e
k
|(nn − I) · e|
2
V
S
0
dr
f
k
ω
k
(9.90)

358 Plasma radiation
where f
k
(v
k
) is the projection of the velocity distribution along k, i.e.
f
k
(v
k
) =
f (v
⊥
,v
k
)dv
⊥
For a Maxwellian distribution the differential scattering cross-section per unit vol-
ume per unit frequency interval is then
d
2
σ
d dω
s
= r
2
e
S(k,ω)sin
2
θ (9.91)
where θ = cos
−1
(n · e) and the scattering ‘form factor’ S(k,ω) is given by the
Gaussian
S(k,ω)=
n
e
k
m
2πk
B
T
e
1/2
exp
−
m ω
2
2k
2
k
B
T
e
(9.92)
In principle the form factor affords a direct measure of the electron distribution
function projected on to k. In practice mapping the distribution function from
measurements of scattered radiation is not usually sufficiently accurate to be
useful. It does however serve to discriminate non-Maxwellian distributions from
Maxwellian. Thomson scattering measurements do allow electron temperature and
electron density to be determined in equilibrium plasmas. The height of the spec-
trum determines the electron density while the half width, or more exactly the full
width at half maximum (FWHM), ω, given by
ω = 4ω
0
2k
B
T
e
mc
2
ln 2
1/2
sin
θ
2
(9.93)
provides a direct measure of electron temperature.
9.7.2 Electron temperature measurements from Thomson scattering
Thomson scattering of laser light is a widely used diagnostic in fusion plasmas,
providing good spatial resolution. The scattered power is proportional to σ
T
n
e
L
where L denotes the length of plasma traversed by the light beam. Given the
smallness of σ
T
this means that only a minute fraction of incident photons will
be scattered. For a density n
e
∼ 10
20
m
−3
and taking L ∼ 0.01 m, the fraction of
photons scattered is only about 10
−10
. Various factors reduce this yet further.
Aside from the requirement that the source of the incident radiation be both
monochromatic and of high brightness, a light scattering diagnostic needs optics
to carry the laser light into the plasma and dispose of it in a beam dump, optics
to collect the scattered light and separate out the different wavelengths, and a
detector. Allowing for the geometry of the collection optics, the efficiency of the
optical system and the quantum efficiency of the detector means that in practice
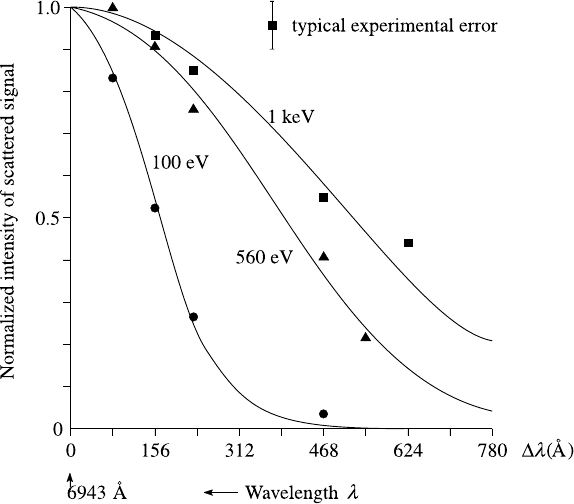
9.7 Scattering of radiation by plasmas 359
Fig. 9.13. Thomson scattering measurements of electron temperature in the T3-A tokamak
(after Peacock et al. (1969)).
the fraction of incident photons collected may be no more than 10
−15
. A key issue
in light scattering experiments is the need to prevent stray light from reaching the
detector, given that the ratio of the scattered power that is detected to the incident
power is so small. One way round this problem is by wavelength discrimination
since stray light, as distinct from scattered light, is not shifted in wavelength. Other
precautions include an arrangement of baffles to reduce light scattered from the
walls and entry port of the input beam and the beam dump. Apart from quantum
noise from both the detector and amplifying electronics, plasma bremsstrahlung
and recombination radiation will be present as background noise at the detector.
Moreover unlike the scattered light, this emission is generated over the plasma as
a whole, not simply from the scattering volume.
A landmark in Thomson scattering experiments was the measurement of electron
temperature in the tokamak T3-A by Peacock et al. (1969). Prior to this experi-
ment, measurements of the plasma energy had been made using a diagmagnetic
diagnostic which is subject to a number of limitations. Thomson scattering estab-
lished beyond doubt that temperatures of the order of 1 keV were reached in early
tokamak experiments. Results from these measurements are shown in Fig. 9.13.
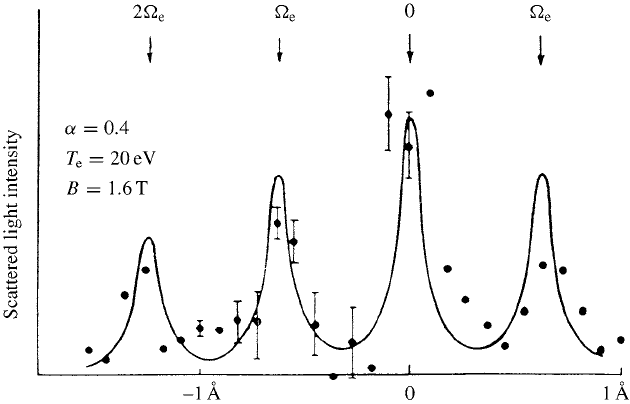
360 Plasma radiation
9.7.3 Effect of a magnetic field on the spectrum of scattered light
The effect of a magnetic field on the scattering form factor (Salpeter (1961), Hag-
fors (1961) and Dougherty, Barron and Farley (1961)) appears only when the wave
vector k is almost orthogonal to the magnetic field B. With this alignment the
spectrum is modulated at integral multiples of the electron cyclotron frequency. As
the orthogonality of k with B weakens, the component of electron motion along the
magnetic field gives rise to a Doppler broadening of the gyro-resonances. Once the
Doppler line width 2(k · b)V
e
, where V
e
is the electron thermal velocity, exceeds
the spacing between the resonances,
e
, the resonances will be smeared out. So a
necessary condition for observing magnetic fine structure is 2kV
e
cos(
ˆ
k · b)
e
.
In practice spatial variation in the magnetic field over the scattering volume may
also result in demodulation.
Magnetic modulation of the spectrum was first detected by Evans and Car-
olan (1970) in an experiment using a relatively dense (n
e
∼ 10
21
m
−3
), cool
(T
e
≈ 20 eV) theta-pinch plasma as a source. With the scattering vector k almost
perpendicular to B the fine structure shown in Fig. 9.14 was resolved. The regularly
spaced peaks show a separation approximately equal to the electron cyclotron
frequency, measured independently by Faraday rotation and corresponding to a
magnetic field of about 1.5 T. Forrest, Carolan and Peacock (1978) subsequently
made use of the sensitivity of the depth of modulation at the cyclotron frequency
to the orthogonality of k and B to measure the direction of the poloidal magnetic
Fig. 9.14. Magnetic modulation of scattered light (after Evans and Carolan (1970)).
9.8 Coherent Thomson scattering 361
field in a tokamak. For the relatively lower densities and much higher temperatures
of tokamak plasmas the flux of scattered light in individual harmonics is too weak
to allow harmonic structure in the scattered light spectrum to be resolved. This
difficulty was overcome using a multiplexing technique due to Sheffield (1975),
in which the free spectral range of a Fabry–Perot interferometer is set equal to
the cyclotron harmonic frequency. The sensitivity of the modulation to the orthog-
onality condition allowed the pitch of the field line to be determined to within
0.15
◦
.
9.8 Coherent Thomson scattering
In treating incoherent Thomson scattering the expression for the total power was
found by summing the contributions from individual electrons, a procedure per-
missible as long as kλ
D
1. This condition ensures that correlations between
plasma particles are unimportant. The next task is to determine the scattering form
factor when collective effects have to be taken into account; this happens when
kλ
D
≤ 1. The summation over the plasma particles has now to be carried out mak-
ing proper allowance for correlations. The need to allow for correlations became
apparent from observations of ionospheric backscatter. Gordon (1958) suggested
that it should be possible to detect Thomson scattering of radar pulses from the
ionosphere. Bowles (1958) found that while the scattered power was in broad
agreement with that predicted, the bandwidth of the scattered signal proved to be
much less than the Doppler width determined by thermal electrons. It appeared
that although the radar pulse was scattered by electrons, their behaviour in turn
was governed by ion dynamics, a result borne out by subsequent studies of the
scattering of radiation by plasma (see Dougherty and Farley (1960), Fejer (1960)
and Salpeter (1960)).
9.8.1 Dressed test particle approach to collective scattering
A helpful way of dealing with coherent Thomson scattering makes use of the con-
cept of test particles. Before dealing with this let us first consider what needs to be
done. When a test charge is introduced into a plasma we know that plasma electrons
and ions react to its presence by forming a shielding cloud around it, resulting in the
test particle being ‘dressed’ by this cloud of particles. We saw in Section 7.8 how
to describe this response in terms of the plasma dielectric function. Our objective
is to determine the spectrum of density fluctuations which governs the form factor
by superposing the fields of all dressed test particles in the plasma. In other words
each electron and ion in turn takes on the role of test particle and the individual
contributions are added up. Since particle correlations have been allowed for by
362 Plasma radiation
means of dressed test particles, these particles themselves are then uncorrelated
so that no further consideration of correlations is needed. A distinction is drawn
between test electrons and test ions. For electrons we have to take account of the
electron itself as well as the electron cloud dressing it. Test ions on the other hand
need not be counted as such since their contribution to scattering is insignificant,
so that only the electron cloud contributes in the case of ions.
Using the results from Section 7.8 a Klimontovich density defined as N
e
≡
f
Ke
(r, v) dv, given by
N
e
(k,ω) =
1
2π
electr ons
j
1 −
χ
e
1 + χ
e
+ χ
i
δ(ω − k · v
j
)
+
Z
2π
ions
l
χ
e
1 + χ
e
+ χ
i
δ(ω − k · v
l
) (9.94)
in which χ
α
denotes the susceptibility of species α. Since we equate coherent
scattering from the plasma with incoherent scattering from a gas of non-interacting
dressed ions and electrons, the spectral power density is now determined by form-
ing the quantity |N
e
(k,ω)|
2
. Introducing the scattering form factor
S(k,ω)= lim
T →∞
V →∞
(2π)
4
TV
|N
e
(k,ω)|
2
n
e
(9.95)
and evaluating (9.95) using (9.94) gives
S(k,ω) =
4
2π
n
e
V
electr ons
j
1 −
χ
e
1 + χ
e
+ χ
i
2
δ(ω − k · v
j
)
+
ions
l
χ
e
1 + χ
e
+ χ
i
2
Z
2
δ(ω − k · v
l
)
5
(9.96)
where the square of the delta functions has been represented in the same way as
in Exercise 9.6. Evaluating the summations of the delta functions in (9.96) using
the representation of the Klimontovich distribution in (7.1) results in contributions
(V/k)
F
K αk
(ω/k)
= (V /k) f
αk
(ω/k), where α = e, i and the subscript k de-
notes the projection of the velocity distribution along k defined in Section 9.7.1.
Then the scattering form factor reduces to
S(k,ω)=
2π
n
e
k
3
1 −
χ
e
1 + χ
e
+ χ
i
2
f
ek
ω
k
+ Z
2
χ
e
1 + χ
e
+ χ
i
2
f
ik
ω
k
(
(9.97)
9.8 Coherent Thomson scattering 363
It remains to evaluate the susceptibilities and hence determine the form factor
explicitly. In the case of a Maxwellian plasma it is straightforward to show that
χ
α
=
ω
2
pα
kV
2
α
1
√
2π
v
V
α
exp(−v
2
/2V
2
α
)
ω − kv
dv
=
1
k
2
λ
2
D
Z
α
n
α
T
e
n
e
T
α
w(ξ
α
) (9.98)
where V
α
= (k
B
T
α
/m
α
)
1/2
is the species thermal speed, ξ
α
= ω/(
√
2kV
α
) and
w(ξ) =
1
√
π
C
ζ e
−ζ
2
dζ
ξ − ζ
is related to the plasma dispersion function defined in Section 7.3.2. For an appro-
priate contour C, w(ξ) may be evaluated to give
w(ξ) = 1 − 2ξ e
−ξ
2
ξ
0
e
ζ
2
dζ + i
√
πξe
−ξ
2
(9.99)
From (9.98) it is evident that for kλ
D
1, χ
α
1 and consequently the form
factor is determined by the O(1) contribution from the first term in (9.97). This
is just the incoherent Thomson scattering discussed in Section 9.7.1. However for
kλ
D
1, χ
e
1 and contributions to S(k,ω) from coherent scattering become
important. For χ
e
1 the entire electron term may be ignored and the sole
contribution to the form factor comes from the ion component.
The spectrum of scattered radiation reflects the collective effects exhibited by the
form factor. For an unmagnetized plasma the resonant denominator corresponds
to electron plasma waves in the region of ω = ω
p
and to ion acoustic waves
in the low frequency range ω ∼ kc
s
, where c
s
is the ion acoustic speed. For
both features the shape of the resonance is determined by Landau and collisional
damping. Electron plasma waves are strongly Landau damped unless kλ
D
1;
in this case one expects a resonant feature at the Langmuir frequency. Under
conditions where Landau damping becomes significant the electron resonance will
be broadened correspondingly. The ion feature in turn reflects the characteristics
of ion acoustic waves which are governed by both ions and electrons. In particular
the ion feature will be weak unless T
e
T
i
to ensure that ion Landau damping is
not severe.
The fact that the two contributions to the spectrum are well separated allows
a simplification to be made in the general expression for S(k,ω) (see Salpeter
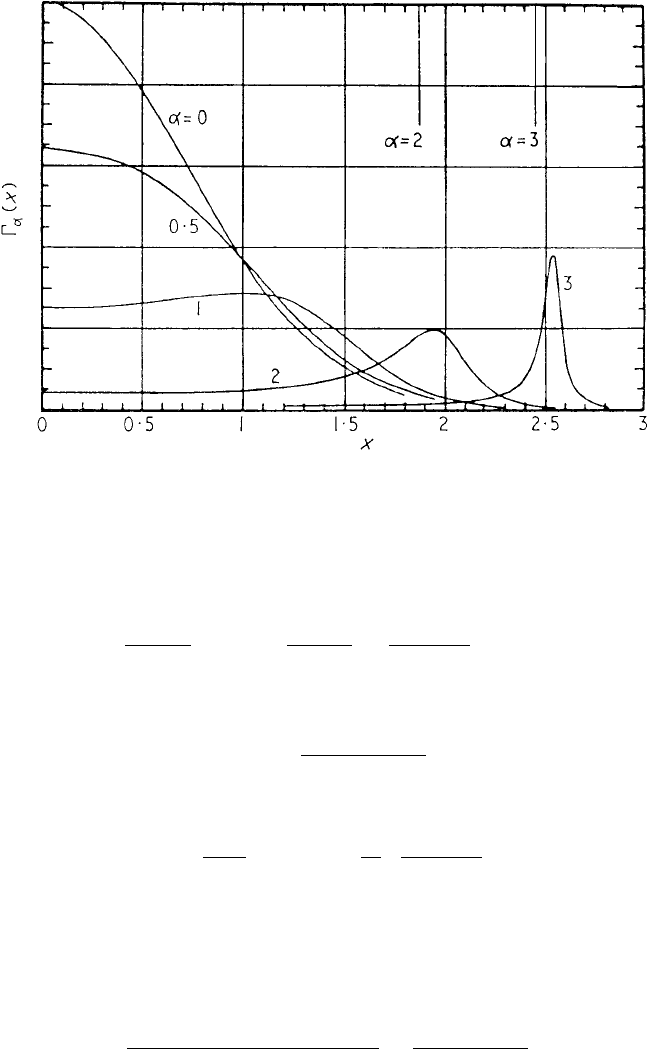
364 Plasma radiation
Fig. 9.15. Salpeter shape function.
(1960)). In the ion term Salpeter set χ
e
∼ 1/(kλ
D
)
2
and in the electron term χ
i
∼ 0.
Then (see Exercise 9.14)
S(k,ω)=
(2π)
1/2
V
e
αe
(ξ
e
) +
(2π)
1/2
V
i
Z
1
1 + k
2
λ
2
D
2
αi
(ξ
i
) (9.100)
in which the shape function
α
(ξ) =
exp(−ξ
2
)
|1 + α
2
w(ξ)|
2
(9.101)
has the same functional form for both the electron and ion features and
α
2
e
=
1
k
2
λ
2
D
α
2
i
= Z
T
e
T
i
1
1 + k
2
λ
2
D
The shape function is represented in Fig. 9.15. The scattering parameter α
e
is an
important index in scattering from plasmas; α
e
1 corresponds to incoherent
Thomson scattering and α
e
1 to cooperative scattering. In terms of the scattering
angle θ = cos
−1
(
ˆ
k
0
·
ˆ
k
s
),
α
e
=
1
(k
2
0
− 2k
0
k
s
cos θ + k
2
s
)
1/2
λ
D
λ
0
4πλ
D
sin θ/2
(9.102)
where λ
0
is the wavelength of the incident radiation.
9.9 Coherent Thomson scattering: experimental verification 365
9.9 Coherent Thomson scattering: experimental verification
It is clear from (9.102) that by varying the scattering angle θ one can pass from
a regime of incoherent Thomson scattering (α
e
1) to one of coherent (or col-
lective) Thomson scattering for which α
e
> 1. Alternatively, for a fixed scattering
geometry one could sweep through α
e
= 1 by switching to longer wavelength
light. In practice this is not usually an option. Substituting values of λ
D
typical
of a moderately dense laboratory plasma with electron temperature of 1 keV, and
choosing λ
0
= 1.06 µm corresponding to neodymium laser light, it follows from
(9.102) that to observe coherent Thomson scattering one has to look close to the
forward direction. In this case the shrinking solid angle sets a limit in practice.
Moreover, stray light problems are exacerbated for small θ. For realistic choices
of scattering angle and laser wavelength, the condition for coherent Thomson
scattering translates into a condition that the electron density n
e
10
22
m
−3
.
Both low and high frequency features in the scattered light spectrum have diag-
nostic potential. The height of electron line provides a measure of electron density
while from the ion resonance we may in principle deduce the ratio of electron to
ion temperatures and hence determine T
i
if T
e
is known from other measurements.
However, as we shall see, the presence of impurity ions may introduce ambiguities
into this measurement.
The first identification of the ion feature in a laboratory plasma was made by
DeSilva, Evans and Forrest (1964) from studies of ruby laser light scattered by a
hydrogen arc plasma. The electron density, needed to characterize α
e
, was mea-
sured independently from Stark broadening of the H
β
line. By detecting scattered
light at two angles it was possible to isolate both incoherent (α
e
1) and coherent
(α
e
> 1) Thomson regimes.
Coherent Thomson scattering diagnostics have been used to advantage in labo-
ratory plasmas, notably in laser-produced plasmas where the high electron density
eases the other constraints, despite difficulties over and above those already out-
lined in Section 9.7.2. Problems may arise on account of the sensitivity of the ion
feature to a number of effects, for example becoming asymmetric due to electron
drift velocities and the presence of impurities in the plasma. In thermal plasmas,
the plasma lines are usually weak features in the spectrum and hence difficult to
resolve. These difficulties notwithstanding, various groups, for example Baldis,
Villeneuve and Walsh (1986), Baldis et al. (1996), Labaune et al. (1995, 1996)),
have used coherent Thomson scattering to characterize ion acoustic waves and
Langmuir waves in laser-produced plasmas.
The distribution worldwide of a number of powerful radar backscatter facilities
has allowed a range of parameters characterizing the ionospheric plasma to be
determined from measurements of Thomson scattering. These include not only
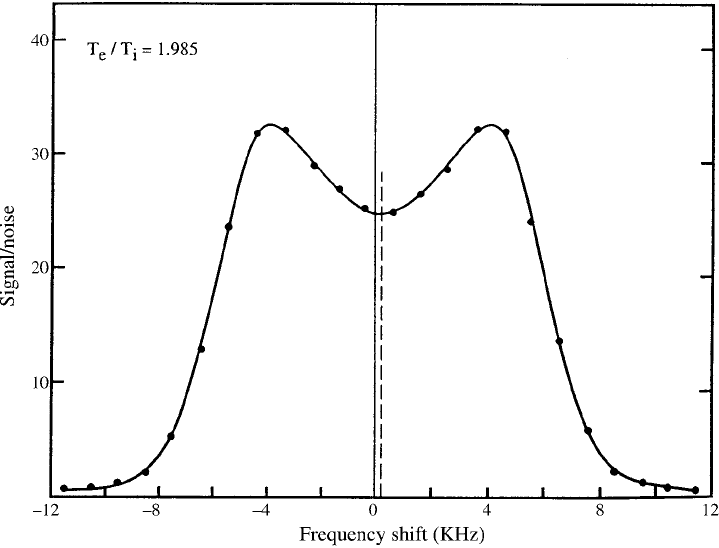
366 Plasma radiation
Fig. 9.16. Radar backscatter spectrum from the ionosphere, taken from an altitude of
300 km on 31 March 1971. The solid line represents the Salpeter spectrum fitted to the
data points (courtesy of J.M. Holt).
electron density and temperature but ion density, ion mass, composition of the
plasma, mean drift velocity and the ion–neutral collision frequency. Figure 9.16
plots radar backscatter data as a function of the frequency shift with the line show-
ing the predicted spectrum. The dashed line denotes the spectral shift resulting
from the mean motion of the ionospheric plasma. This spectrum was recorded
from a height of 300 km, where O
+
is the only ion of significance and this helped
minimize deviations from the Salpeter spectrum due to other ions being present.
Above this height, protons and He
+
ions from the solar wind increasingly affect
the composition of plasma in the high ionosphere. In lower regions plasma compo-
sition is governed by the photochemistry of the ionosphere. The effects of plasma
composition on the scattering form factor were first discussed by Moorcroft (1963).
9.9.1 Deviations from the Salpeter form factor for the ion feature: impurity ions
Impurity ions are present to some extent in all laboratory plasmas. Given their
greater mass and consequently lower thermal velocities, impurities serve to en-
