Boyd T.J.M., Sanderson J.J. The Physics of Plasmas
Подождите немного. Документ загружается.

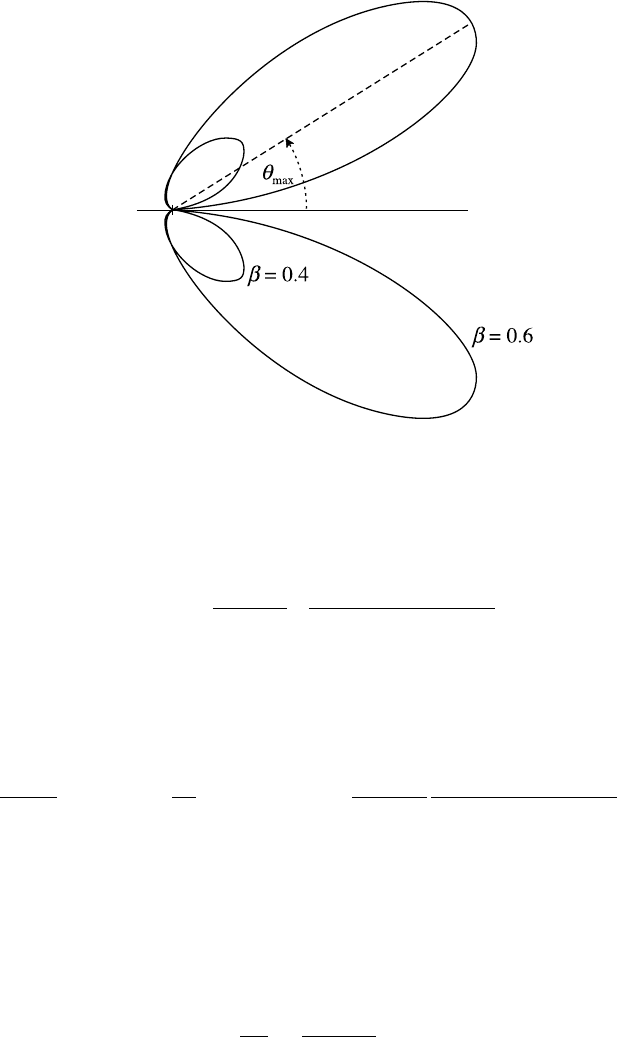
9.2 Electrodynamics of radiation fields 327
Fig. 9.2. Polar diagram of the instantaneous power radiated by an accelerated charged
particle; θ
max
denotes the angle at which peak power is radiated.
where
S · n =
e
2
16π
2
ε
0
c
|n ×{(n −β
β
β) ×
˙
β
β
β}|
2
g
6
R
2
ret
(9.12)
Note that (dP(t)/d) d denotes the radiated power measured by the observer at
time t due to emission by the charge at time t
. It is often useful to consider power
as a function of the retarded time t
.Then
dP(t
)
d
= (S · n)R
2
dt
dt
= g(S ·n)R
2
=
e
2
16π
2
ε
0
c
|n ×{(n −β
β
β) ×
˙
β
β
β}|
2
g
5
(9.13)
Relativistic effects appear both in the numerator and, through g, in the denominator.
In the ultra-relativistic limit (β → 1) the effect of the denominator is dominant
in determining the radiation pattern; the dipole distribution familiar from the non-
relativistic limit deforms with the lobes inclined increasingly forward as in Fig. 9.2.
In the non-relativistic limit g → 1 and we recover the dipole distribution
dP
d
=
e
2
˙
β
2
16π
2
ε
0
c
sin
2
θ (9.14)
where θ is the angle between
˙
β
β
β and n.

328 Plasma radiation
Larmor’s formula for the power radiated in all directions follows on integrating
over solid angle, i.e.
P =
dP
d
d =
e
2
˙v
2
6πε
0
c
3
(9.15)
The corresponding relativistic expression for the radiated power may be found by
replacing (9.15) by its covariant form, giving
P =
e
2
6πε
0
m
2
c
3
d p
µ
dτ
d p
µ
dτ
=
e
2
6πε
0
c
[(
˙
β
β
β)
2
− (β
β
β ×
˙
β
β
β)
2
]
(1 − β
2
)
3
(9.16)
Much of our discussion will focus on the distinct characteristics of radiation from
particles accelerated in the plasma micro-electric fields and in any magnetic fields
present. Where plasmas are subject to external electromagnetic fields the incident
radiation is scattered, with the scattering governed by the Thomson cross-section
σ
T
=
8π
3
r
2
e
(9.17)
where the classical electron radius r
e
= (e
2
/4πε
0
mc
2
).
9.2.2 Frequency spectrum of radiation from an accelerated charge
We consider next how the radiated energy is distributed in frequency. Since the
spectrum is represented in terms of frequencies at a detector it is natural to revert
to using time t (the observer’s time). Then
dP(t)
d
=
e
2
16π
2
ε
0
c
|n ×{(n −β
β
β) ×
˙
β
β
β}|
2
g
6
ret
≡|a(t)|
2
(9.18)
The energy radiated per unit solid angle dW/d is found by integrating (9.18) over
time, giving
dW
d
=
∞
−∞
|a(t)|
2
dt (9.19)
Introducing the Fourier transform of a(t)
a(ω) =
1
√
(2π)
∞
−∞
a(t)e
iωt
dt (9.20)
and using Parseval’s theorem allows us to represent the energy radiated per unit
solid angle as
dW
d
=
∞
−∞
|a(ω)|
2
dω (9.21)
9.2 Electrodynamics of radiation fields 329
Thus
dW
d
=
∞
0
[|a(ω)|
2
+|a(−ω)|
2
]dω = 2
∞
0
|a(ω)|
2
dω (9.22)
The energy radiated per unit solid angle per unit angular frequency interval is then
d
2
W
d dω
= 2|a(ω)
2
| (9.23)
Finding a(ω) from (9.20) is simplified if we change the variable of integration from
t to t
, so removing the evaluation of the term in square brackets at the retarded
time; then
a(ω) =
e
2
32π
3
ε
0
c
1/2
∞
−∞
exp
iω
t
+
R(t
)
c
n ×{(n −β
β
β) ×
˙
β
β
β}
g
2
dt
(9.24)
Since we wish to determine the spectrum in the radiation zone (r r
0
in Fig. 9.1),
n is effectively time-independent and R(t
) r − n ·r
0
(t
) so that
d
2
W (ω, n)
d dω
=
e
2
16π
3
ε
0
c
∞
−∞
exp
iω
t
−
n · r
0
(t
)
c
n ×{(n −β
β
β) ×
˙
β
β
β}
g
2
dt
2
(9.25)
Thus the energy radiated per unit solid angle per unit frequency interval is deter-
mined as a function of ω and n once r
0
(t
) is prescribed.
For purposes of calculation, we cast (9.25) in a slightly different form. Using the
representation (see Exercise 9.1)
n ×{(n −β
β
β) ×
˙
β
β
β}
g
2
=
d
dt
n × (n ×β
β
β)
g
we integrate (9.25) by parts to find, in the radiation zone,
d
2
W (ω, n)
d dω
=
e
2
ω
2
16π
3
ε
0
c
∞
−∞
exp
iω
t
−
n · r
0
(t
)
c
[n × (n ×β
β
β)]dt
2
(9.26)
The results summarized in this section provide a basis for the formalism needed
to describe radiation emitted by charged particles. Much of the rest of the chapter
is taken up with the characteristics of emission from particles moving in particular
fields. Emission is of course only part of the story. Plasmas in thermal equilib-
rium that emit radiation absorb it as well and details of absorption mechanisms
are crucial for the radiative heating of plasmas as we shall see in Chapter 11.
Before discussing the emission of radiation we first summarize some ideas central
to radiation transport in plasmas.
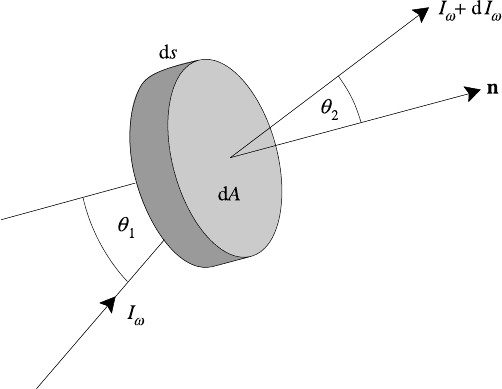
330 Plasma radiation
9.3 Radiation transport in a plasma
Fig. 9.3. Pencil of radiation refracted across an element of plasma.
The general problem of radiation transport in plasmas is complicated but fortu-
nately for our purposes does not need to be discussed in detail. For simplicity
we ignore scattering and take account of emission and absorption in the transport
equation. This is strictly valid only under conditions of local thermodynamic equi-
librium (LTE), a concept to be introduced later in this section.
The equation of radiative transfer can be thought of as an expression of energy
conservation in terms of geometric optics. If F
ω
denotes the spectral density of the
radiation flux then, by energy conservation in steady state,
∇·F
ω
= 0 (9.27)
Note that F
ω
has dimensions of power per unit area per angular frequency interval.
The principal assumption in geometric optics is that the properties of the medium
vary slowly with position; that is, the scale length of variations is very much greater
than the wavelength of radiation in the medium. In this approximation, one may
picture the radiation being transported along rays. Figure 9.3 shows an element of
plasma of cross-section dA, thickness ds and n is the unit normal outwards from
the surface. The net radiation flux across this element is
dF
ω
· n = dF
ω
cos θ = I
ω
(s) cos θ d (9.28)
I
ω
(s) is the intensity of the radiation and s denotes displacement along the ray. Its

9.3 Radiation transport in a plasma 331
importance in radiation transport is due to the fact that it can be measured more or
less directly. I
ω
(s) is defined by
dP
ω
(s) = I
ω
(s) cos θ d dω d A
where dP
ω
is the time-averaged power in the spectral range dω crossing an area dA
within a cone of solid angle d. I
ω
is expressed in units of watts per square metre
per steradian per unit angular frequency. In general, the intensity is a function both
of direction and position in the medium. When it is a function of position alone,
the radiation is said to be isotropic.
Suppose the plasma through which the radiation is passing is loss-free and
isotropic but slightly inhomogeneous so that a ray, on passing through the element
of plasma shown in Fig. 9.3, suffers bending. Then, by energy conservation,
(I
ω
+ dI
ω
) cos θ
2
d
2
dω dA − I
ω
cos θ
1
d
1
dω dA = 0 (9.29)
supposing no reflection of energy at the interface takes place. Now from Snell’s
law, n sin θ is constant (where n is the refractive index) along the ray. Then, since
d
2
d
1
=
sin θ
2
dθ
2
sin θ
1
dθ
1
=
sin θ
2
sin θ
1
n
1
cos θ
1
n
2
cos θ
2
=
n
1
n
2
2
cos θ
1
cos θ
2
(9.29) leads to
I
ω2
n
1
n
2
2
cos θ
1
d
1
= I
ω1
cos θ
1
d
1
so that
I
ω
n
2
= const. (9.30)
along a ray path in a slowly varying inhomogeneous, isotropic, transparent
medium. At frequencies much greater than the plasma frequency, n
2
1 and (9.30)
simplifies to I
ω
= const. along a ray path. The result for an anisotropic plasma is
more complicated since Snell’s law is no longer obeyed in general but holds only
for waves propagating in certain directions relative to the magnetic field.
Next we relax the requirement that the plasma be both source-free and loss-free.
Within the geometrical optics representation we introduce absorption and emission
terms on the right-hand side of (9.27). Let α
ω
be the absorption coefficient per
unit path length in the plasma, so that a radiative flux I
ω
dA d suffers a loss
α
ω
I
ω
dA d ds in travelling a distance ds. Similarly we introduce an emission co-
efficient
ω
defined so that
ω
dA d ds is the emission from the elemental volume
into solid angle d in the direction of the ray. Then,
dI
ω
ds
=
∂ I
ω
∂s
− α
ω
I
ω
+
ω
(9.31)
332 Plasma radiation
Now, ∂ I
ω
/∂s is the rate of change of I
ω
due to the change in refractive index along
a ray path; from (9.30)
∂ I
ω
∂s
=
2I
ω
n
dn
ds
so that
n
2
d
ds
I
ω
n
2
=
ω
− α
ω
I
ω
(9.32)
This is the radiative transport equation.
To solve the transfer equation, we introduce a source function
S
ω
=
1
n
2
ω
α
ω
(9.33)
and define an optical depth τ
τ =
τ
dτ =−
s
α
ω
ds (9.34)
in which the minus sign denotes that the optical depth is measured back into the
plasma along the ray path. Then (9.32) reads
d
dτ
I
ω
n
2
=
I
ω
n
2
− S
ω
(9.35)
Integrating along the ray path in the plasma between points A and B one has,
I
ω
(A)
n
2
(A)
e
−τ(A)
=
I
ω
(B)
n
2
(B)
e
−τ(B)
+
τ(B)
τ(A)
S
ω
(τ )e
−τ
dτ (9.36)
In practice it may be permissible to ignore curvature of the ray path where changes
in refractivity are negligible. Where A, B are points on a plasma–vacuum boundary
as in Fig. 9.4 then τ(A) = 0, τ(B) = τ
0
, the total optical depth of the plasma, and
n(A) = 1 = n(B). Thus, neglecting reflection at the boundaries, the emergent
intensity is
I
em
ω
= I
inc
ω
e
−τ
0
+
τ
0
0
S
ω
(τ )e
−τ
dτ (9.37)
The first term on the right-hand side takes account of absorption of the incident
radiation while the second represents contributions from sources within the plasma,
again allowing for absorption of radiation in transit from its origin to the point A.
When I
inc
ω
= 0,
I
em
ω
=
τ
0
0
S
ω
(τ )e
−τ
dτ (9.38)
Two important limiting cases of this result correspond to τ
0
1, when the plasma
is said to be optically thin and the opposite limit τ
0
1, when it is optically
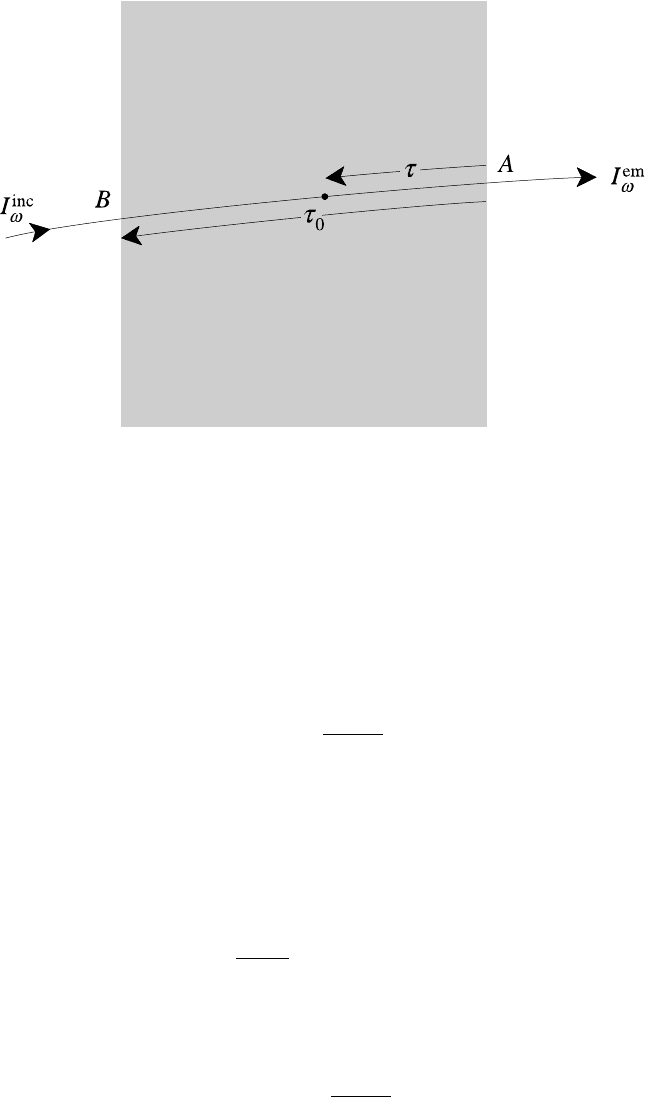
9.3 Radiation transport in a plasma 333
Fig. 9.4. Ray path through the plasma.
thick. In the optically thin limit, absorption along a ray path is negligible so that
the emergent intensity is simply the sum of contributions along the ray, i.e.,
I
em
ω
s
A
s
B
ω
(s)ds (9.39)
In the optically thick limit τ
0
→∞so that after integrating (9.38) by parts
I
em
ω
=
ω
(s
A
)
α
ω
(s
A
)
(9.40)
In other words the intensity affords a direct measure of the source function. Be-
tween these two limits one has to solve the radiative transfer equation to determine
the intensity of the radiation observed at a detector.
A medium in thermal equilibrium that is perfectly absorbing emits radiation that
is Planckian, i.e. the intensity I (ω) = B(ω) where
B(ω) =
¯
hω
3
8π
3
c
2
[exp(
¯
hω/k
B
T ) − 1]
−1
(9.41)
is the black body intensity (for a single polarization) and
¯
h = h/2π where h is
Planck’s constant. In the classical limit (9.41) reduces to the Rayleigh–Jeans form
B(ω) =
ω
2
k
B
T
8π
3
c
2
(9.42)

334 Plasma radiation
Then from (9.40) we find
ω
α
ω
=
ω
2
k
B
T
r
8π
3
c
2
(9.43)
which defines a radiation temperature T
r
.
By and large radiation emitted by laboratory plasmas, unlike that from stellar
sources, does not correspond to a black body spectrum. We have to abandon the
notion of global thermal equilibrium for something less complete, local thermody-
namic equilibrium (LTE), a concept that lends itself to about as many definitions as
it finds application! Broadly speaking, homogeneous plasmas can be assumed to be
in an LTE state when collision processes are dominant. The radiation field is locally
Planckian with temperature T
e
. Only under LTE conditions is the source function
ω
/α
ω
= B(ω). In reality of course laboratory plasmas are rarely homogeneous
and this imposes additional restrictions on the validity of LTE.
It is still possible to describe the radiation field locally by a temperature T
e
even when the temperature is globally non-uniform. This means that the region
concerned has to be sufficiently local for the temperature to be considered uniform
while at the same time extensive enough for thermodynamics to be valid. The LTE
approximation breaks down when the source function is no longer a local function
of electron temperature but depends on the radiative flux from other regions of the
plasma.
9.4 Plasma bremsstrahlung
We turn next to the principal sources of radiation from fully ionized plasmas,
bremsstrahlung and, with magnetic fields present, cyclotron or synchrotron ra-
diation. We shall deal with these separately, since the spectral characteristics in
each case are quite distinct. The spectral range of bremsstrahlung is very wide,
extending from just above the plasma frequency into the X-ray continuum for
typical plasma temperatures. By contrast the cyclotron spectrum is characterized
by line emission at low harmonics of the Larmor frequency. Synchrotron spectra
from relativistic electrons display distinctive characteristics as we shall see later
on. Moreover, whereas cyclotron and synchrotron radiation can be dealt with
classically, the dynamics being treated relativistically in the case of synchrotron
radiation, bremsstrahlung from plasmas has to be interpreted quantum mechan-
ically, though not usually relativistically. Bremsstrahlung results from electrons
undergoing transitions between two states of the continuum in the field of an
ion (or atom). Oppenheimer (1970) has described bremsstrahlung graphically as
the shaking off of quanta from the field of an electron that suffers a sudden
jerk.

9.4 Plasma bremsstrahlung 335
In place of a full quantum mechanical treatment we opt instead for a semi-
classical model of bremsstrahlung which turns out to be adequate for most plasmas.
Classically we can think of bremsstrahlung in terms of the emisssion of radiation
by an electron undergoing acceleration in the field of a positive ion. The classical
emission spectrum can then be massaged to agree with the quantum mechanical
spectrum by multiplying by a correction factor, the Gaunt factor.
To see what is involved let us make an estimate of plasma bremsstrahlung from
a simple model in which an electron moves in the Coulomb field of a single
stationary ion of charge Ze. Then
|
˙
v|=
Ze
2
4πε
0
mr
2
and substituting in Larmor’s formula (9.15), the power radiated by the electron is
given by
P
e
=
e
2
6πε
0
c
3
Ze
2
4πε
0
mr
2
2
(9.44)
If we take the spatial distribution of the plasma electrons about the ion to be uni-
form, then the contribution to the bremsstrahlung from all electrons in encounters
with this test ion is found by summing the individual contributions to give,
P =
8π Z
2
e
6
n
e
3(4πε
0
)
3
m
2
c
3
∞
r
min
dr
r
2
=
8π Z
2
e
6
n
e
3(4πε
0
)
3
m
2
c
3
r
min
The cut-off at r = r
min
is needed to avoid divergence. A value for r
min
may be
chosen in a number of ways and we shall see later that plasma bremsstrahlung is not
sensitive to this choice. For present purposes we take r
min
λ
deB
, the de Broglie
wavelength, the distance over which an electron may no longer be regarded as a
classical particle. For a thermal electron
λ
deB
∼
¯
h/(mk
B
T
e
)
1/2
where T
e
is the electron temperature. Thus
P
8π Z
2
e
6
n
e
3(4πε
0
)
3
mc
3
¯
h
k
B
T
e
m
1
2
If n
i
denotes the ion density, the total bremsstrahlung power radiated per unit
volume of plasma, P
ff
, is then
P
ff
=
8π
3
Z
2
n
e
n
i
mc
3
¯
h
e
2
4πε
0
3
k
B
T
e
m
1
2
= 5.34 × 10
−37
Z
2
n
e
n
i
T
1/2
e
(keV) Wm
−3
(9.45)

336 Plasma radiation
We see that the power radiated as bremsstrahlung is proportional to the product
of electron and ion densities and to Z
2
. Thus any high Z impurities present will
contribute bremsstrahlung losses disproportionate to their concentrations. Note that
since electron–electron collisions do not alter the total electron momentum they
make no contribution to bremsstrahlung in the dipole approximation.
9.4.1 Plasma bremsstrahlung spectrum: classical picture
The exact classical treatment of an electron moving in the Coulomb field of an
ion is a standard problem in electrodynamics. Provided the energy radiated as
bremsstrahlung is a negligibly small fraction of the electron energy (we treat the ion
as stationary) the electron orbit is hyperbolic and the power spectrum dP(ω)/dω
from a test electron colliding with plasma ions of density n
i
may be shown to
be
dP(ω)
dω
=
16π
3
√
3
Z
2
n
i
m
2
c
3
e
2
4πε
0
3
1
v
G(ωb
0
/v) (9.46)
where b
0
= Ze
2
/4πε
0
mv
2
is the impact parameter for 90
◦
scattering, v the incident
velocity of the electron and G(ωb
0
/v) a dimensionless factor, known as the Gaunt
factor, which varies only weakly with ω.
Most of the bremsstrahlung is emitted at peak electron acceleration, i.e. at the
distance of closest approach to the ion. Collisions described by a small impact
parameter produce hard photons; less energetic photons come from distant encoun-
ters, with correspondingly large impact parameters. Denoting the impact parameter
by b, collisions producing hard photons correspond to b b
0
and the electron orbit
is approximately parabolic. In the opposite limit b b
0
, the electron trajectory is
more or less linear and in reality it is only in this limit that a classical picture of
bremsstrahlung is justified. For an electron following the linear trajectory shown
in Fig. 9.5, r
2
(t) = (vt)
2
+ b
2
. The components of the acceleration normal and
parallel to the trajectory are,
˙v
⊥
(t) =
Ze
2
4πε
0
m
b
[(vt)
2
+ b
2
]
3/2
˙v
(t) =
Ze
2
4πε
0
m
vt
[(vt)
2
+ b
2
]
3/2
Integrating (9.26) over the solid angle allows us to express the energy radiated per
unit frequency interval in the non-relativistic limit as
dW (ω)
dω
=
e
2
6π
2
ε
0
c
3
∞
−∞
˙
v(t)e
iωt
dt
2
