Boyd T.J.M., Sanderson J.J. The Physics of Plasmas
Подождите немного. Документ загружается.


8.6 Collisional relaxation 317
by (W )
2
, we find
∂
(W )
2
∂t
= m
2
V
2
∂
2
G
∂V
2
= 2m
2
V
s
n
s
z
2
s
(a
s
V )
=
s
ν
E
s
mV
2
2
2
(8.48)
say, defining collision coefficients ν
E
s
for energy exchange. Thus,
ν
E
s
(V ) =
8n
s
z
2
s
(a
s
V )
V
3
(8.49)
Since [φ(1) − (1)] ≈ 0.6 and (1) ≈ 0.2, comparing (8.47) and (8.49) we see
that for thermal speeds ν
E
ee
∼ ν
ee
and ν
E
ii
∼ ν
ii
. On the other hand, energy exchange
between ions and electrons is the least efficient process since at most a fraction
(m
e
/m
i
) of the kinetic energy involved in a collision can be transferred from one
particle to the other. For thermal speeds, low Z and T
e
∼ T
i
we find
ν
E
ee
: ν
E
ii
: ν
E
ei
(∼ ν
E
ie
) ∼ 1:
m
e
m
i
1/2
:
m
e
m
i
Thus, in an anisotropic plasma with unequal electron and ion temperatures, the
electrons will relax to a Maxwellian distribution within a few electron–electron
collision times followed by the ions in a few ion–ion collision times and finally,
after a time of order (m
i
/m
e
)ν
−1
ee
, equilibration of the electron and ion temperatures
takes place.
8.6 Collisional relaxation
The collision frequencies derived in the previous section are useful for making
order of magnitude calculations but their velocity dependence means that the actual
time taken for the relaxation of the high velocity part of a distribution function
to a Maxwellian can be very much greater than the ‘thermal speed’ estimate.
Numerical studies have shown that typically these estimates are good for the bulk
of the distribution out to approximately twice the thermal speed but beyond that
relaxation is progressively much slower. The assumption, usually made even for
collisionless plasmas, that the distribution function is approximately Maxwellian
is, therefore, often not sustainable. Consequently, there has long been an interest in
feasible alternative distribution functions.

318 Collisional kinetic theory
One important example is the self-similar distribution function of order s defined
as
f
s
(v) =
c
s
n
π
3/2
v
3
s
exp(−v
s
/v
s
s
)
The constants c
s
and v
s
are given by
c
s
=
3π
1/2
4(1 + 3/s)
v
2
s
=
k
B
Ts(1 + 3/s)
m(5/s)
where n is the particle number density and (x) is the gamma function. It is easily
seen that s = 2 corresponds to the Maxwellian distribution.
Jones (1980), Langdon (1980) and Balescu (1982) have shown that laser-
irradiated high Z plasmas reach a self-similar state with s = 5 for the electrons
and s = 2 for the ions. Compared with the Maxwellian, self-similar distributions
with s > 0 (also known as super-Gaussian distributions) are flat-topped and for
this reason they have been of interest to space-plasma physicists in explaining the
frequently observed electron distributions at the Earth’s bow shock (Feldman et
al. (1983)). In weak turbulence theory, anomalous transport coefficients have been
derived from self-similar distributions (see Dum (1978)).
As we have seen in this chapter and will discuss more extensively in Chapter 12,
the derivation of transport coefficients is directly related to the relaxation of the dis-
tribution function and involves the calculation of its velocity moments. For this rea-
son in particular there has been considerable analytical and numerical investigation
of the collisional relaxation of non-Maxwellian distribution functions. Analytical
progress depends upon some simplifying assumption, usually that the distribution
function remains in the same class of function (e.g. remains self-similar but with
varying s) throughout the relaxation. Given our remarks in the opening paragraph
of this section, this is hardly likely to be the case and numerical studies based on
the Fokker–Planck equation have confirmed this suspicion. As an illustration we
shall consider two examples of temperature equalization in a single species plasma.
Plasmas with two-temperature velocity distributions are created in the laboratory
in heating processes and occur naturally in space.
The isotropic two-temperature distribution function
f (v
2
) = f
c
(v
2
;n
c
, T
c
) + f
h
(v
2
;n
h
, T
h
)
where both f
c
and f
h
are Maxwell distributions (8.4) and the subscripts denote cold
and hot components, is used for plasmas created, for example, by the injection of
a hot plasma into a cooler, background plasma. It has been noted in numerical
simulations of such plasmas that the temperatures of the separate components
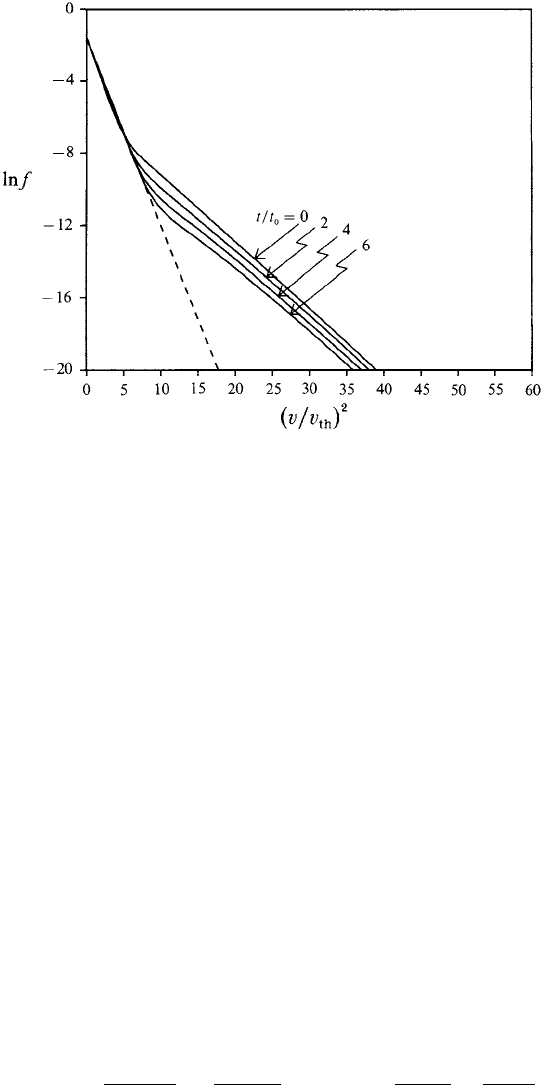
8.6 Collisional relaxation 319
Fig. 8.7. Relaxation of isotropic two-temperature plasma (after McGowan and Sanderson
(1992)).
change much more slowly than their densities. McGowan and Sanderson (1992)
modelled their evolution by
f (v
2
, t) = f (v
2
;n(t), T ) + f
c
(v
2
;n
c
(t), T
c
) + f
h
(v
2
;n
h
(t), T
h
)
where all three components are Maxwellians with constant temperatures but vari-
able densities. The total number density n
0
and the average (or final) temperature
T are then given by
n
0
= n(t) + n
c
(t) + n
h
(t)
n
0
T = n(t)T + n
c
(t)T
c
+ n
h
(t)T
h
representing the conservation of particles and energy. Initially n(0) = 0 and finally
n(∞) = n
0
, this component having grown at the expense of the other two for
which n
c
(∞) = n
h
(∞) = 0. The collisional relaxation of such a plasma was
shown to be well-represented by this model and is illustrated in Fig. 8.7, where the
hot component appears as a succession of straight lines of constant slope (constant
T
h
).
The anisotropic, two-temperature distribution most widely used is the bi-
Maxwellian distribution, introduced in Section 8.2.2,
f (v) = n
0
m
2πk
B
T
⊥
m
2πk
B
T
1/2
exp
−
mv
2
⊥
2k
B
T
⊥
−
mv
2
2k
B
T
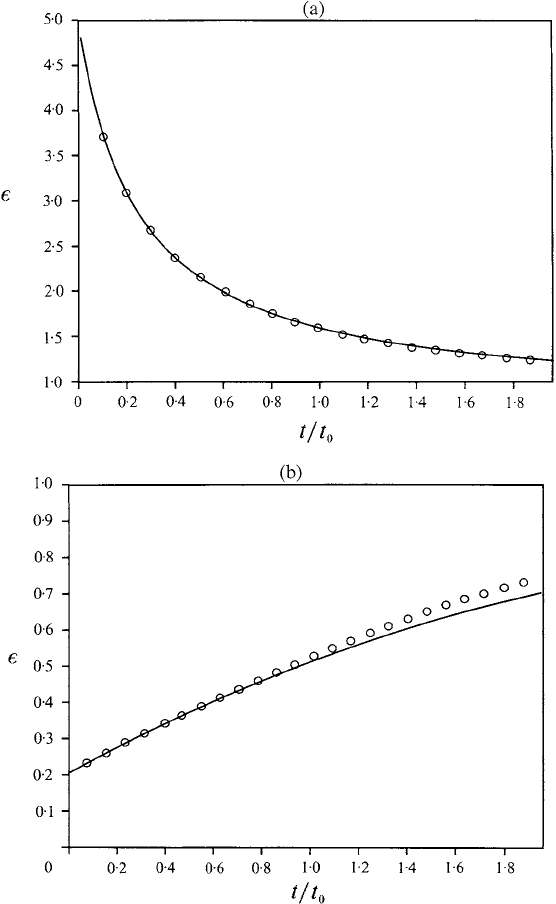
320 Collisional kinetic theory
Fig. 8.8. Relaxation of a bi-Maxwellian plasma for (a) = 5 (oblate distribution) and (b)
= 0.2 (prolate distribution) (after McGowan and Sanderson (1992)).
Here the anisotropy introduced by a strong magnetic field enables the velocity
distributions for motion along the field lines (v
) and across the field lines (v
⊥
)
to differ significantly.

Exercises 321
Schamel et al. (1989), following earlier work by Kogan (1961) derived an evo-
lution equation for the relaxation of a bi-Maxwellian distribution in terms of the
anisotropy parameter = T
⊥
/T
. The equation is
d
dτ
=
(1 + 2)
5/2
4(1 − )
[(2 + )g() − 3] (8.50)
where
g() =
tanh
−1
| − 1|
1/2
| − 1|
1/2
τ = ν
E
t
ν
E
=
8π
1/2
n(Ze)
4
ln
(3mk
3
B
T
3
)
1/2
ε
2
0
However, this assumes that the distribution function remains bi-Maxwellian. Nu-
merical studies by Jorna and Wood (1987) and McGowan and Sanderson (1992)
have shown that this is not a valid assumption, especially for the prolate case <1.
Despite this, the evolution equation, which involves moments of the distribution
function, does give reliable results for the oblate case (>1) where the moments
are less sensitive to the departures from bi-Maxwellian form. In Fig. 8.8 solid lines
denote the numerical results while the circles are points determined analytically
from (8.50).
Exercises
8.1 Repeat the calculation of electrical conductivity σ carried out in Sec-
tion 8.2 but allowing for a velocity dependent collision frequency. Show
that the result is
σ =
Z
2
e
2
12πε
0
k
B
T
v
2
f
M
dv
ν
c
(v)
8.2 Explain physically why you would expect the ions to determine the coef-
ficient of viscosity in a plasma but the electrons to determine the electrical
and thermal transport coefficients.
What property of a plasma leads to ion determination of the ambipolar
diffusion coefficient?
8.3 In neoclassical transport show that the fraction of particles performing
banana orbits is proportional to the square root of the inverse aspect ratio.
8.4 Show that the cumulative effect of weak collisions in a plasma outweighs
the effect of rare strong interactions by comparing the mean time for a
single π/2 deflection with the plasma collision time ν
−1
c
.
8.5 Verify (8.35) and hence obtain (8.36).

322 Collisional kinetic theory
8.6 By carrying out the integrations by parts, show that in (8.37) the term in
G gives no contribution to dynamical friction and that in H gives none to
diffusion.
8.7 By adding a driving term −(eE/m) · ∂ f /∂v to the left-hand side of (8.37)
and taking the first-order moment, as in the derivation of (8.39), find the
relationship between the velocity V and field strength E for electron run-
away (i.e. such that ∂V/∂t > 0).
8.8 Show that the Fokker–Planck equation that describes the evolution of the
electron velocity distribution function f
e
(v, t) for collisions with station-
ary massive ions may be written
∂ f
e
∂t
c
=
n
e
Ze
4
ln
8πε
2
0
m
2
∂
∂v
·
v
2
I − vv
v
3
·
∂ f
e
∂v
Using this obtain an expression for the resistivity when the plasma is
perturbed by a time-dependent electric field E = E
0
cos ωt. To do this
write f
e
(v) = f
0
(v) + f
1
(v) cos θ , where θ is the angle between E
0
and v,
and show that
f
1
(v) =
ieE
0
m
∂ f
0
∂v
ω +
in
e
Ze
4
ln
4πε
2
0
m
2
v
3
−1
From f
1
(v) write down the perturbed current density j
1
and form j
1
·E
to determine the average rate at which energy is absorbed by the plasma.
Balancing this against the rate of loss of field energy, νε
0
E
2
/2 where ν
denotes the energy damping rate and assuming that in absorbing energy
the electron distribution remains Maxwellian, show that ν = (ω
2
pe
/ω
2
)ν
ei
where
ν
ei
=
Zn
e
e
4
ln
4
√
2πε
2
0
m
1/2
T
3/2
e
8.9 Plasmas are often heated by ion beams (injected as neutral atoms) with
energies in the 100 keV range, i.e. an order of magnitude greater than the
plasma thermal energy. Within this range the beam velocity V is inter-
mediate between ion and electron thermal velocities, i.e. V
i
< V < V
e
.
Collisions between beam ions and plasma ions and electrons slow the beam
through frictional drag and scattering off plasma ions deflects the beam.
Assuming that frictional drag dominates over velocity diffusion show
that the Fokker–Planck equation for the distribution of beam ions, f
b
(v, t),
takes the form
∂ f
b
∂t
= A
∂
∂V
·
V
V
3
1 +
V
3
V
3
c
f
b

Exercises 323
where A = ZZ
2
b
n
e
e
4
ln /4πε
2
0
m
i
m
b
and V
c
= (3
√
π Z /2)
1/3
×(T
3
e
/m
e
m
2
i
)
1/6
.
8.10 Can you suggest why, in the relaxation of a bi-Maxwellian distribution
function, the oblate case (>1) is less sensitive than the prolate case
(<1) to the fact that the distribution does not remain bi-Maxwellian?
9
Plasma radiation
9.1 Introduction
We know from classical electrodynamics that accelerated charged particles are
sources of electromagnetic radiation. Particles accelerated in electric or mag-
netic fields radiate with distinct characteristics. Electric micro-fields present in the
plasma result in bremsstrahlung emission by plasma electrons. External radiation
fields interacting with the plasma give rise to scattered radiation. Charged particles
moving in magnetic fields emit cyclotron or synchrotron radiation, depending on
the energy range of the particles.
The interaction of radiation with plasmas in all its aspects – emission, absorp-
tion, scattering and transport – is a key to understanding many effects in both
laboratory and natural plasmas. Laboratory plasmas in particular do not radiate as
black bodies so that an integrated treatment of emission, absorption and transport
of radiation is usually needed. Core plasma parameters such as electron and ion
temperatures and densities as well as plasma electric and magnetic fields may
all be determined spectroscopically, in the most general sense of the term. Rather
arbitrarily we shall confine our discussion to radiation from fully ionized plasmas
thus excluding line radiation on which many diagnostic procedures are based. To
some extent alternative spectroscopic techniques, in particular light scattering, have
replaced if not entirely supplanted measurements of line radiation as preferred
diagnostics of some key parameters in fusion plasmas (see Hutchinson (1988)).
In the course of this chapter we shall outline the basis of some of these diagnostics,
notably those that rely on bremsstrahlung and cyclotron radiation as well as those
involving light scattering. We shall limit our discussion of radiation to plasmas in
thermal equilibrium, with few exceptions. Non-thermal emission, while an impor-
tant issue in practice, is in many instances still relatively poorly understood.
324

9.2 Electrodynamics of radiation fields 325
9.2 Electrodynamics of radiation fields
We begin with a statement of the results of Maxwellian electrodynamics essential
to an understanding of radiation fields. Details of the derivations leading to these
results are included in Exercise 9.1. The potentials A and φ are determined by
∇
2
−
1
c
2
∂
2
∂t
2
A =−µ
0
j
∇
2
−
1
c
2
∂
2
∂t
2
φ =−
q
ε
0
(9.1)
with specified current and charge sources together with the Lorentz gauge condi-
tion
∇ · A +
1
c
2
∂φ
∂t
= 0 (9.2)
The solutions to (9.1) are expressed in terms of the retarded potentials:
A(r, t) =
µ
0
4π
[j(r
, t
)]
t
=t−|r−r
|/c
|r − r
|
dr
φ(r, t) =
1
4πε
0
[q(r
, t
)]
t
=t−|r−r
|/c
|r − r
|
dr
(9.3)
Consider now a source consisting of a single particle of charge e moving arbitrarily
with velocity
˙
r
0
(t) at a point r
0
(t). Then
j(r, t) = e
˙
r
0
(t)δ(r −r
0
(t)) q(r, t) = eδ(r − r
0
(t)) (9.4)
Substituting in (9.3) we find
A(r, t) =
µ
0
4π
evc
cR − v ·R
t
=t−R(t
)/c
(9.5)
φ(r, t) =
1
4πε
0
ec
cR − v ·R
t
=t−R(t
)/c
(9.6)
where R(t
) =|r − r
0
(t
)| and v(t
) =
˙
r
0
(t
). These expressions are the Li
´
enard–
Wiechert potentials. Using the retarded potentials the electric field E(r, t) may be
expressed in a form due to Feynman:
E(r, t) =
e
4πε
0
n
R
2
+
R
c
d
dt
n
R
2
+
1
c
2
d
2
n
dt
2
ret
(9.7)
where n(t
) is the unit vector from the source to the field point in Fig. 9.1 and
ret denotes that the expression within the square brackets must be evaluated at the
retarded time t
= t − R(t
)/c. The first term in (9.7) represents the Coulomb
field of the charge e at its retarded position. The second is a correction to the
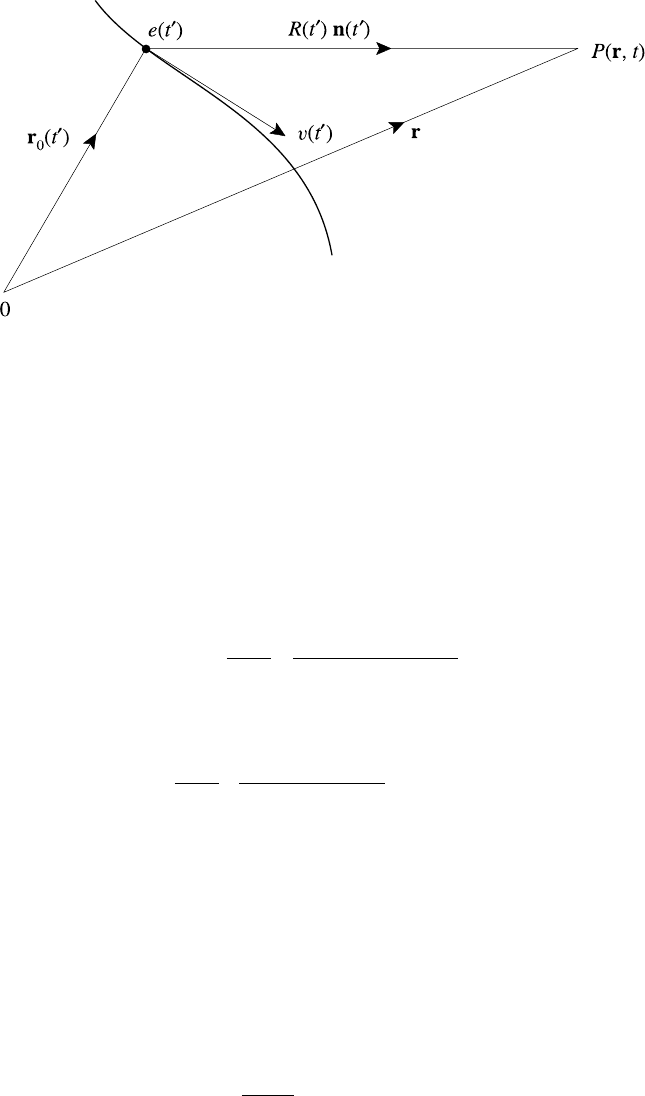
326 Plasma radiation
Fig. 9.1. Source–observer geometry for a radiating charged particle.
retarded Coulomb field, being the product of the rate of change of this field and the
retardation delay time R/c. Thus the first and the second terms together correspond
to the retarded Coulomb field advanced in time by R/c, namely to the observer’s
time t. In other words, for fields varying slowly enough these two terms represent
the instantaneous Coulomb field of the charge. The final term, the second time
derivative of the unit vector from the retarded position of the charge to the observer,
contains the radiation electric field E
rad
∝ R
−1
, i.e.
E
rad
(r, t) =
e
4πε
0
n ×{(n −β
β
β) ×
˙
β
β
β}
cg
3
R
ret
(9.8)
where g = (1 − n ·β
β
β). The total electric field is
E(r, t) =
e
4πε
0
(1 − β
2
)(n −β
β
β)
g
3
R
2
ret
+ E
rad
(r, t) (9.9)
9.2.1 Power radiated by an accelerated charge
Once the radiation field is known, we can construct the Poynting vector S and so
determine the instantaneous flux of energy (see Section 6.2)
S = E × H = cε
0
|E
rad
|
2
n (9.10)
with E
rad
given by (9.8). Thus the power P, radiated per unit solid angle ,is
dP(t)
d
= (S · n)R
2
(9.11)
