Boyd T.J.M., Sanderson J.J. The Physics of Plasmas
Подождите немного. Документ загружается.


9.5 Electron cyclotron radiation 347
frequency together with harmonics. The relative intensities of the harmonics de-
pend on electron temperature. The term in braces, the shape function, governs line
shapes with the line width ω determined by Doppler broadening
ω ∼ l(2k
B
T
e
/mc
2
)
1/2
cos θ
Thus by measuring the width of the cyclotron line or its harmonics we may de-
termine the electron temperature. Note that when cos θ<β, line widths will be
determined by the relativistic mass increase. The shape function for a relativisti-
cally broadened line is distinct from the Doppler line shape, being both narrower
and asymmetric. Other mechanisms can and do contribute to line broadening across
the range of plasma parameters. However, if we confine our interest to ECE from
fusion plasmas we may disregard radiation broadening due to loss of energy by an
electron as it radiates and collision broadening, since collisions contribute in only
a small way to line widths in hot plasmas.
9.5.2 ECE as tokamak diagnostic
When it comes to using ECE as a diagnostic for electron temperature in toka-
maks, other considerations come into play. Two in particular need to be taken
into account. The first concerns line broadening due to the spatially inhomoge-
neous magnetic field of a tokamak which may dominate Doppler and relativistic
broadening in determining the line width. Tokamak magnetic fields are determined
largely by the toroidal component B
t
(R) ∝ R
−1
. The fact that this field is known
accurately means that emission at ω = l(R) is characterized by good spatial
resolution. Thus the electron temperature profile can be determined. Normally only
the first few harmonic lines are used in contemporary tokamaks and these may be
optically thick or optically thin or somewhere in between. For optically thick lines
the temperature profile is determined directly (from (9.42)), i.e.
k
B
T
e
(R) =
8π
3
c
2
l
2
2
(R
0
)
R
R
0
2
I
lR
0
(R
0
)
R
(9.66)
A second consideration comes from the need to allow for aspects of wave
propagation in plasmas introduced in Chapters 6 and 7. Effects in inhomogeneous
and bounded plasmas will be discussed in Chapter 11. More particularly, a kinetic
theory formulation is needed to deal with absorption in hot plasmas. Moreover,
account needs to be taken of reflection at the walls and at the divertor so that in
practice a detailed picture of propagation has to be found using a toroidal ray-
tracing code.
In principle, ECE measurements using optically thin harmonics allow the plasma
density to be inferred once the temperature has been found from an optically thick
348 Plasma radiation
harmonic measurement. This follows since the optical depth is a function both
of the temperature and density. However multiple reflection of the optically thin
radiation at the walls makes this less straightforward in practice than might at first
appear.
ECE offers further diagnostic potential through polarization measurements that
allow determination of the direction of the magnetic field inside the plasma at the
position at which the radiation is emitted. However, should the plasma density be
large enough to cause strong birefringence, the radiation, instead of retaining its
source polarization, reflects the polarization that characterizes the field point. If
that happens what we end up with is the direction of the magnetic field at the edge
of the plasma, rather than at the point of emission.
For tokamaks operating at higher temperatures, the use of second harmonic ECE
to measure the temperature profile suffers from harmonic overlap. As the temper-
ature increases, emission at higher harmonics contributes increasingly to the spec-
trum so that the weakly relativistic condition lβ 1 may no longer be satisfied.
Higher harmonic contributions then change the characteristics of the spectrum, as
we shall find in the following section. Moreover, the presence of even a small
population of suprathermal electrons leads to changes in the cyclotron emission,
disproportionate to the numbers involved. For non-thermal plasmas, emission and
absorption are no longer related by Kirchhoff’s law and have to be determined
independently. In cases where the electron distribution is characterized by a hot
electron tail on a bulk Maxwellian distribution, it is in principle possible to discrim-
inate between thermal and suprathermal contributions to ECE by measurements at
right angles to the magnetic field using an optically thick harmonic.
9.6 Synchrotron radiation
We shall separate our discussion of synchrotron radiation into two ranges, one
characterized by electron energies ranging from some tens to a few hundred keV
and the other in which electron energies are ultra-relativistic. The moderately rel-
ativistic range is of interest in that it includes, at the lower end, electron energies
expected in the next generation of tokamaks. The ultra-relativistic range is largely
of astrophysical interest. Analyzing spectra in both relativistic regimes is possible
only by making various approximations and in general the synchrotron radiation
spectrum has to be found numerically.
9.6.1 Synchrotron radiation from hot plasmas
We return to the general expression for the spectral power density given in (9.60)
and for simplicity set θ = π/2, since this choice corresponds to peak synchrotron
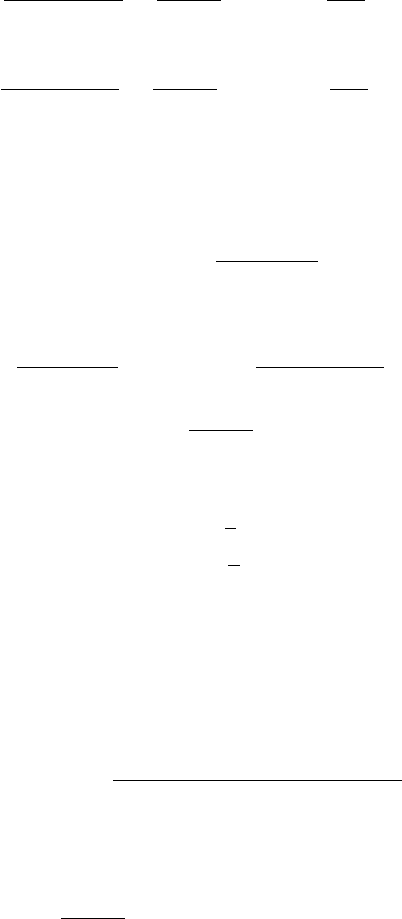
9.6 Synchrotron radiation 349
emission. We identify the contributions from the O(E B
0
) and X (E ⊥B
0
) modes,
namely
dP
O
(ω, π/2)
dω
=
e
2
ω
2
8π
2
ε
0
c
∞
l=1
β
2
J
2
l
ωβ
⊥
δ(ω −l) (9.67)
dP
X
(ω, π/2)
dω
=
e
2
ω
2
8π
2
ε
0
c
∞
l=1
β
2
⊥
J
2
l
ωβ
⊥
δ(ω −l) (9.68)
The synchrotron emission coefficient
S
(ω) may be found from (9.67), (9.68) by
averaging over the distribution function f (p). If we assume an isotropic distribu-
tion then, dropping the π/2 signature
(O,X)
S
(ω) =
∞
0
dP
(O,X)
(ω)
dω
f ( p) p
2
d p (9.69)
with
dP
(O,X)
(ω)
dω
= 2π
π
0
dP
(O,X)
(ω, ϑ)
dω
sin ϑ dϑ
=
e
2
ω
2
8π
2
ε
0
c
∞
l=1
A
(O,X)
l
(γ )δ(ω −l) (9.70)
where
A
(O,X)
l
(γ ) = 2πβ
2
π
0
J
2
l
ω
β sin ϑ
cos
2
ϑ
J
2
l
ω
β sin ϑ
sin
2
ϑ
sin ϑ dϑ (9.71)
and ϑ denotes the angle between B
0
and p. Explicit forms for A
(O,X)
l
(γ ) were
found by Trubnikov (1958) for three ranges of electron energy: non-relativistic
(lβ 1), moderately relativistic (γ
3
l) and ultra-relativistic (γ 1, l 1).
To determine the plasma emission coefficient for moderately relativistic elec-
trons we use (9.69) with the relativistic Maxwellian distribution function
f ( p) =
N exp[−( p
2
c
2
+ m
2
c
4
)
1/2
/k
B
T
e
]
4π(k
B
T
e
)
2
(m/c)yK
2
(y)
(9.72)
where y = mc
2
/k
B
T
e
and K
2
(y) is a modified Bessel function. The plasma emis-
sion coefficient is then
(O,X)
S
(ω) =
e
2
ω
2
8π
2
ε
0
c
∞
0
∞
l=1
A
(O,X)
l
(γ ) δ[ω − l] f (p) p
2
d p (9.73)
with the representation for A
(O,X)
appropriate to this energy range (γ
3
l)
given by Trubnikov (1958). Evaluating (9.73) is straightforward and with an upper
350 Plasma radiation
Fig. 9.8. Emission spectrum for radiation by moderately relativistic electrons before and
after summation over the harmonics (after Hirshfield, Baldwin and Brown (1961)).
limit for electron energies consistent with the assumption y 1, the synchrotron
emission at θ = π/2isgivenby
(O,X)
S
(ω,
π
2
) =
ω
2
p
0
c
ω
2
k
B
T
8π
3
c
2
∞
l=1
(l, x, y) (9.74)
where
(l, x, y) =
√
2π y
5/2
l
2
x
4
(l
2
− x
2
)
1/2
A
(O,X)
l
l
x
exp
−y
l
x
− 1
(9.75)
with x = ω/
0
, denotes the Trubnikov function.
The emission spectrum is governed by the Trubnikov function. Figure 9.8 plots
(l, x, 10) for the first twenty harmonics of the X-mode as a function of x; y = 10
corresponds to an electron temperature of about 50 keV. The emission spectrum
shows discrete harmonic structure below some critical value l
c
beyond which
structure is smoothed on account of harmonic overlap. Individual harmonics are
now only approximately Gaussian near maximum intensities with a half-width
ω
l
l
3/2
(k
B
T/mc
2
)
0
for small l. The lines are subject to a relativistic broaden-

9.6 Synchrotron radiation 351
ing (due to the relativistic change of mass) which increases with harmonic number
and which has the effect of making the shape function asymmetric.
For electron temperatures above about 10 keV ECE becomes less useful as
a diagnostic on account of harmonic overlap. Fidone and Granata (1994) have
proposed using synchrotron radiation (ESE) as an alternative diagnostic for next-
generation tokamaks. ESE offers several advantages in that high harmonics are
unaffected by cut-offs and the ray paths are effectively straight lines.
9.6.2 Synchrotron emission by ultra-relativistic electrons
Synchrotron radiation by electrons of ultra-relativistic energies, γ 1, was first
suggested as a source of cosmic radio waves by Alfv
´
en and Herlofson (1950) and
by Kiepenheuer (1950) and later used by Shklovsky (1953) to interpret the radio
spectrum from the Crab nebula. It is helpful to see first of all how the principal
characteristics of the emission in this regime can be established qualitatively from
a simple model. In particular it is easy to show that the radiation is focused within
a cone of aperture angle ∼ γ
−1
about the direction of the instantaneous velocity of
the electron. From the Li
´
enard–Wiechert potential (9.5) it is clear that the denomi-
nator becomes small as θ = cos
−1
(
ˆ
v·
ˆ
R) tends to zero. This property determines the
character of the radiation field which has the form of a sequence of pulses emitted
at that point on the orbit at which the radiation is beamed towards the observer.
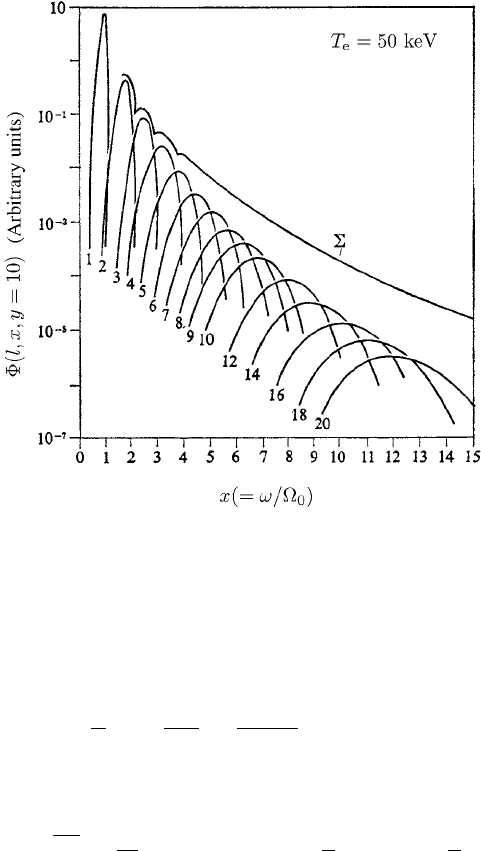
Figure 9.9 illustrates the essential feature, namely that an observer sees the electron
only through flashes of radiation emitted as it transits a small segment of its orbit.
The radiation field is governed by the maximum value of A
⊥
, the component of A
perpendicular to n:
|A
⊥
|=
µ
0
4π R
evc sin θ
c − v cos θ
These maxima occur at θ
max
±γ
−1
and since γ 1 for highly relativistic
electrons, it follows that the synchrotron emission is beamed strongly into a narrow
cone about the forward direction in what is sometimes referred to as the ‘lighthouse
effect’.
This result enables us to determine the pulse width t
. As seen by the observer,
the pulse switches on at time t
1
= (R + vt
)/c, and ends at the later time t
2
=
2t
+ (R − vt
)/c.Theobserved pulse width t is therefore
t = 2t
1 −
v
c
= 2t
/γ
2
1 +
v
c
Now t
= θ
m
/ = 1/γ and since v/c ∼ 1
t (γ
3
)
−1
= (γ
2
0
)
−1
352 Plasma radiation
Fig. 9.9. Instantaneous synchrotron radiation beamed from an ultra-relativistic electron
(the ‘lighthouse effect’).
The radiation spectrum is made up from a sequence of pulses at intervals τ =
2π/ t. The emission is linearly polarized and, on the basis of the argument
presented, we expect the emission to peak at a frequency
ν
c
=
ω
c
2π
1
2π
γ
3
(9.76)
For frequencies above this the spectrum should show a cut-off so that (9.76) pro-
vides a measure of the width of the synchrotron spectrum.
Returning to the general result for the synchrotron power radiated by an electron,
it is possible to apply the ultra-relativistic criterion together with the requirement
l 1 to show that in this limit with β
= 0 one can reduce (9.62) to
P
UR
l
=
e
2
2
0
4π
2
√
3ε
0
c
l
γ
4
∞
2l/3γ
3
K
5/3
(y) dy (9.77)
Here K
5/3
(y) is a modified Bessel function. Since harmonics are now very closely
spaced it makes more sense to recast (9.77) to show the power radiated per unit
frequency rather than per harmonic. This gives
dP
UR
(ω)
dω
=
√
3e
2
0
8π
2
ε
0
c
ω
ω
c
∞
ω/ω
c
K
5/3
(y) dy (9.78)
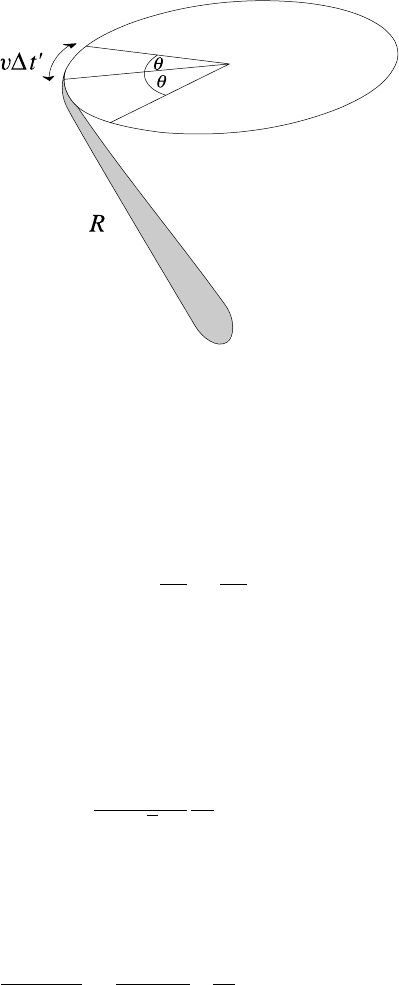
For ω/ω
c
1, dP
UR
(ω)/dω ∝ (ω/ω
c
)
1/3
while in the opposite limit ω/ω
c
1,
dP
UR
(ω)/dω ∝ (ω/ω
c
)
1/2
exp(−ω/ω
c
). The shape function determining the spec-
trum across the range is shown in Fig. 9.10.
9.6 Synchrotron radiation 353
Fig. 9.10. Shape function S(ω/ω
c
) for synchrotron radiation spectrum in the ultra-
relativistic limit.
To determine the spectrum in this limit we need to know the electron energy
distribution. A clue to the distribution follows from the observation that energetic
electrons in supernovae remnants are sources of cosmic rays and the observed
cosmic ray energy spectrum is well represented by a power law. If we suppose
that this reflects the electron energy distribution in the source, then
N (E)dE = CE
−δ
dE (9.79)
where N (E)dE denotes the number of electrons with energy in the range (E, E +
dE) and δ is a constant. Balancing the radiation emitted against electron energy
loss, it is straightforward to show that the intensity of synchrotron emission is given
by
I (ν)dν = K
1
B
(δ+1)/2
⊥
ν
−(δ−1)/2
dν (9.80)
We conclude from this analysis that an electron energy spectrum with a power law
dependence E
−δ
generates a synchrotron spectrum I (ν) ∝ ν
−α
with a spectral
index
α =
1
2
(δ − 1)
354 Plasma radiation
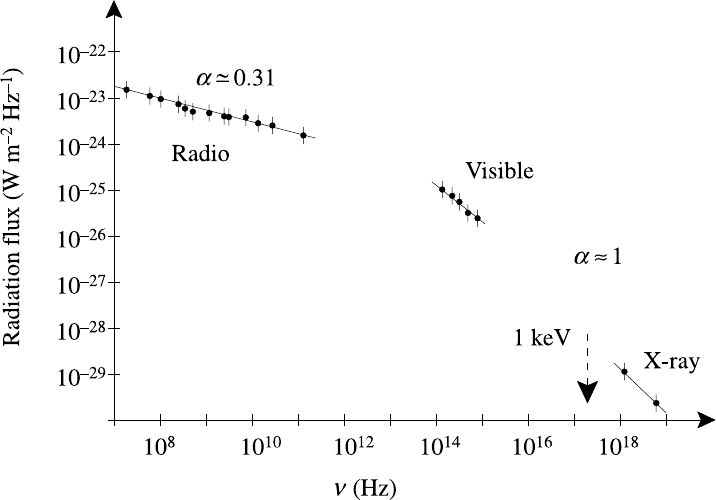
Fig. 9.11. Synchrotron emission spectrum from the Crab nebula.
The observed power law dependence of radio spectra together with the strong linear
polarization of the radiation make a compelling case for interpreting the emission
in terms of a synchrotron mechanism.
A typical emission spectrum from the Crab nebula is shown in Fig. 9.11.
Comparison with the bremsstrahlung spectrum shows that the source is non-
thermal; in general the contribution from thermal sources to radiation emitted by
supernova remnants is negligible. The observed radio emission is represented by a
power law dependence, I
ν
∝ ν
−α
, over a wide range of frequencies. The spectral
index generally lies in the range 0.3–1.5 depending on the source. The spectral
range is very wide, extending up to frequencies in the hard gamma-ray region. The
gaps are due to absorption in the atmosphere. The marked change in spectral index
at ν ∼ 10
13
Hz is indication of a difference in the energy distribution of electrons
from those responsible for the radio spectrum. This in turn reflects the different
populations, one associated with the supernova explosion itself, the source of the
other being the rotating magnetic neutron star. The pulsar injects highly relativistic
electrons into the nebula. Synchrotron self-absorption, unimportant for the X-ray
region, becomes significant at radio frequencies and distorts the spectrum from a
simple power law representation.

9.7 Scattering of radiation by plasmas 355
9.7 Scattering of radiation by plasmas
We next consider ways in which radiation is scattered by plasmas. A plane
monochromatic electromagnetic wave incident on a free electron at rest is scat-
tered, the scattered wave having the same frequency as the incident radiation;
the scattering cross-section is defined by the Thomson cross-section, (9.17). For
scattering by electrons the Thomson cross-section has the value 6.65 × 10
−29
m
2
;
scattering by ions, being at least six orders of magnitude smaller, rarely matters in
practice.
Thomson scattering results in a force driving the electron in the direction of the
incident wave (see Landau and Lifschitz (1962)). The electron ‘absorbs’ energy
from the wave at the average rate Sσ
T
. Thus, the electron gains momentum from
the wave at a rate Sσ
T
/c. On the other hand, the rate at which momentum is radi-
ated by the electron is c
−1
dP/dn d, so that from (9.14) the total momentum
of the scattered wave is zero. The final result, therefore, is equivalent to a force on
the electron of magnitude
Sσ
T
c
=
4π
3
ε
0
E
2
0
r
2
e
in the direction of the incident wave. This phenomenon is known as radiation
pressure and provides a small correction to the Lorentz equation.
9.7.1 Incoherent Thomson scattering
In practice we have to find an expression for the Thomson scattering cross-section
from all the electrons contained within a finite volume of plasma. Since Thomson
scattering is a key diagnostic for high temperature plasmas this needs in general
to be treated relativistically. Nevertheless, the non-relativistic limit is widely used
for electron temperatures up to several keV and is simpler to deal with analytically.
In this limit of (9.8) the scattered electric field E
s
is given in terms of an incident
electromagnetic field E
i
(r, t) = E
0
exp i(k
0
·r −ω
0
t) by the dipole approximation
E
s
(r, t) =
r
e
R
n × (n × E
i
)
ret
= [(r
e
/R)(nn − I) · E
i
]
ret
(9.81)
where I denotes the unit dyadic. In a relativistic formulation we may retain the
format of (9.81), substituting a generalized polarization dyadic P for (nn − I) so
that
E
s
(r, t) =
r
e
R
P · E
i
ret
(9.82)
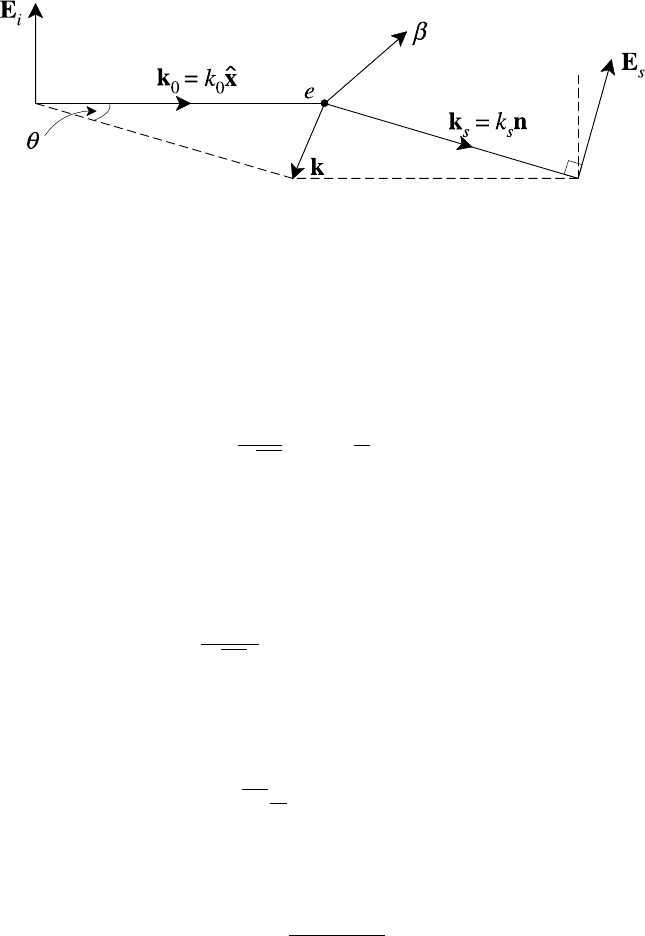
356 Plasma radiation
Fig. 9.12. Scattering geometry.
To find a representation for P we have to return to the relativistic expression (9.8)
with
˙
β
β
β determined by the Lorentz equation as in Exercise 2.9. The Fourier time
transform of (9.82) determines the frequency spectrum of the scattered field over
an interval T :
E
s
(r,ω
s
) =
1
√
2π
T/2
−T /2
r
e
R
P · E
i
ret
e
iω
s
t
dt (9.83)
To proceed it is simpler to re-cast (9.83) in terms of the retarded time, t
, which in
the usual radiation (far-field) approximation becomes t
t − (r − n · r
0
(t
))/c
(see Fig. 9.1). In this approximation, R r and the scattered field may then be
represented as
E
s
(r,ω
s
) =
r
e
e
ik
s
·r
√
2πr
T
/2
−T
/2
gP(t
) · E
0
e
i(ωt
−k·r
0
(t
))
dt
(9.84)
where k
s
= ω
s
n/c, ω = ω
s
− ω
0
and k = k
s
− k
0
. We now assume that over the
interval T
the particle velocity v is effectively constant so that r
0
(t
) = r
0
(0)+vt
.
If we disregard the initial displacement, (9.84) becomes
E
s
(r,ω
s
) =
√
2π
r
e
r
e
ik
s
·r
g(P · E
0
)δ(ω− k · v) (9.85)
Explicitly, the scattered frequency ω
s
= ω
0
+ (k
s
− k
0
) · v so that for an incident
wave propagating in the x-direction (see Fig. 9.12),
ω
s
=
(1 −
ˆ
x ·β
β
β)
(1 − n ·β
β
β)
ω
0
or, to first order in β,
ω
s
= ω
0
(1 − (
ˆ
x − n) ·β
β
β) ≡ ω
D
(9.86)
The Doppler-shifted frequency ω
D
of the incident wave combines the effect of elec-
tron motion both along the propagation vector of the incident wave (down-shifting
