Boyd T.J.M., Sanderson J.J. The Physics of Plasmas
Подождите немного. Документ загружается.


9.4 Plasma bremsstrahlung 337
Fig. 9.5. Linear electron trajectory.
=
e
2
6π
2
ε
0
c
3
Ze
2
4πε
0
m
2
∞
−∞
be
⊥
+ vte
[(vt)
2
+ b
2
]
3/2
e
iωt
dt
2
=
2e
2
ω
2
3π
2
ε
0
c
3
Ze
2
4πε
0
mv
2
2
K
2
1
ωb
v
+ K
2
0
ωb
v
(9.47)
where K
0
and K
1
are modified Bessel functions of the second kind (see Exer-
cise 9.5).
The bremsstrahlung emitted by the test electron from distant encounters with all
the plasma ions is then found by integrating over a suitably defined range of the
impact parameter. The number of encounters with ions per second having impact
parameters between b and b +db is 2π n
i
vb db, so that the power radiated (per unit
frequency interval) by a single electron is
dP(ω)
dω
= 2π
b
max
b
min
dW (ω)
dω
n
i
vb db
Choices have to be made for the limits to the impact parameter. For consistency
with the approximation by a linear trajectory we identify b
min
with b
0
and take
b
max
= v/ω corresponding to the width of the bremsstrahlung spectrum. The
bremsstrahlung from all plasma electrons is found by integrating over the electron
distribution function. Assuming Maxwellian electrons we can carry out the integra-
tions over impact parameter and electron velocity to determine the bremsstrahlung
emission coefficient. The emission coefficient
ω
is the power radiated per unit
volume per unit solid angle per unit (angular) frequency and, in the low frequency

338 Plasma radiation
limit, is given by
ω
=
8
3
√
3
Z
2
n
e
n
i
m
2
c
3
e
2
4πε
0
3
m
2πk
B
T
e
1
2
¯g (9.48)
and ¯g is the Maxwellian-averaged Gaunt factor. In our case
¯g(ω, T
e
) =
√
3
π
ln
2m
ζω
4πε
0
Ze
2
2k
B
T
e
ζ m
3
2
(9.49)
where ln ζ = 0.577 is Euler’s constant and the factor (2/ζ ) 1.12 in the argument
of the logarithm has been included to make ¯g in (9.49) agree with the exact low
frequency limit determined from (9.46). The factor
√
3/π is introduced into (9.49)
to conform with the conventional definition of the Gaunt factor in the quantum
mechanical treatment.
9.4.2 Plasma bremsstrahlung spectrum: quantum mechanical picture
While the classical description of bremsstrahlung is useful in the low frequency
range, at high frequencies a quantum mechanical formulation is needed. For
present purposes it is enough to treat the electron as a wave packet. In the same
spirit, the quantum nature of radiation is allowed for through the photon limit. In
the simple model used at the start of Section 9.4 to illustrate the dependence of
bremsstrahlung on plasma parameters we chose the de Broglie wavelength as a
cut-off impact parameter. This choice is dictated by the Uncertainty Principle since
an electron with momentum p can be determined only to within an uncertainty
x ∼
¯
h/ p ∼ λ
deB
, the de Broglie wavelength. So for impact parameters b ≤ x
we need a quantal picture of bremsstrahlung.
In Section 9.4.1 we found the plasma bremsstrahlung emissivity by averaging
over a Maxwellian distribution function. Here we have to allow for the fact that
there can be no bremsstrahlung emission at frequencies above the photon limit,
ω = mv
2
/2
¯
h; in other words a photon of energy
¯
hω can only be emitted by an
electron with energy at least
¯
hω. Consequently averaging the Gaunt factor G(ω, v)
over a Maxwellian distribution gives
¯g(ω, T
e
) =
∞
0
g(ω, v) f (v)v dv =
∞
0
g(ω, E )e
−E/k
B
T
e
d(E/k
B
T
e
) (9.50)
and with proper allowance made for the photon limit, we require g(ω, E) = 0for
E <
¯
hω. Writing E = E
+
¯
hω, and normalizing so that = E /k
B
T
e
we find from
(9.50)
¯g(ω, T
e
) =
∞
0
g
ω,
+
¯
hω
k
B
T
e
e
−
d
e
−
¯
hω/k
B
T
e
9.4 Plasma bremsstrahlung 339
It is customary to show the exponential dependence on electron temperature explic-
itly in the expression for the emission coefficient so that the Maxwellian-averaged
Gaunt factor is then defined as
¯g(ω, T
e
) =
∞
0
g
ω,
+
¯
hω
k
B
T
e
e
−
d
(9.51)
Simple analytic representations can be found in limiting cases. At low frequencies
and high electron temperatures (but not so high that electron thermal velocities
become relativistic)
¯g(ω, T
e
) =
√
3
π
ln
4
ζ
k
B
T
e
¯
hω
(9.52)
At high frequencies a Born (plane wave) approximation (equivalent to represent-
ing the electron trajectory as a straight line) is commonly used. A more general
expression has been given by Elwert (see Griem (1964)). The Born approximation
results in a Gaunt factor
¯g
B
(ω, T
e
) =
√
3
π
K
0
¯
hω
2k
B
T
e
e
¯
hω/2k
B
T
e
(9.53)
This reduces to (9.52) in the low frequency limit.
The bremsstrahlung emission coefficient is represented in terms of the Gaunt
factor (in whatever approximation) as
ω
(T
e
) =
8
3
√
3
Z
2
n
e
n
i
m
2
c
3
e
2
4πε
0
3
m
2πk
B
T
e
1/2
¯g(ω, T
e
)e
−
¯
hω/k
B
T
e
(9.54)
The Gaunt factor is a relatively slowly varying function of
¯
hω/k
B
T
e
over a
wide range of parameters which means that the dependence of bremsstrahlung
emission on frequency and temperature is largely governed by the factor
(m/2π k
B
T
e
)
1/2
exp(−
¯
hω/k
B
T
e
) in (9.54). For laboratory plasmas with electron
temperatures in the keV range, the bremsstrahlung spectrum extends into the X-ray
region of the spectrum.
9.4.3 Recombination radiation
Although we have excluded line radiation from our discussion of plasma radiation
we need to consider briefly free–bound transitions leading to recombination radia-
tion. The final state of the electron is now a bound state of the atom (or ion, if the ion
was initially multiply ionized). The kinetic energy of the electron together with the
difference in energy between the final quantum state n and the ionization energy
of the atom or ion now appears as photon energy. This event involving electron
capture is known as radiative recombination and the emission as recombination

340 Plasma radiation
radiation. In certain circumstances, recombination radiation may dominate over
bremsstrahlung.
It is again useful to follow a semi-classical argument to arrive at an emission
coefficient for recombination radiation. Essentially one takes the corresponding
bremsstrahlung coefficient and applies the correspondence principle to introduce
the bound final state in place of a continuum level. The correspondence principle
is essentially a statement that quantum mechanical results must reduce to their
classical limits when the density of quantum states is high. In that event we can
think of a free–bound transition in terms of bremsstrahlung formalism adjusted to
allow for the contribution to the photon energy of the additional energy released
through recombination. The free–bound spectrum consists of lines corresponding
to
¯
hω
n
= mv
2
/2 + Z
2
R
y
/n
2
where R
y
is the Rydberg constant. The correspon-
dence principle attributes the power radiated classically to the line spectrum as
opposed to the continuum in the case of bremsstrahlung. The energy correspond-
ing to a transition from the continuum to a quantum state n may be shown to
be
¯
hω
n
2Z
2
R
y
n
3
(9.55)
for large n (see Exercise 9.5).
The energy emitted in a transition to a quantum level n is then written
(dW/dω)
class
× ω
n
where (dW/dω)
class
is the same as the expression used to
calculate the bremsstrahlung emission. As in that case we can then proceed to
integrate over the impact parameter. The power emitted as recombination radiation
to level n by the plasma electrons is found by integrating over the distribution
function. For a Maxwellian distribution this amounts to evaluating
∞
0
exp
−
E
k
B
T
e
δ
E −
¯
hω −
Z
2
R
y
n
2
dE
The emission coefficient for recombination radiation to level n for a thermal plasma
is then
n
(ω, T
e
) =
8
3
√
3
Z
2
n
e
n
i
m
2
c
3
e
2
4πε
0
3
m
2πk
B
T
e
1/2
exp(−
¯
hω/k
B
T
e
)
×
Z
2
R
y
k
B
T
e
2g
n
n
3
exp(Z
2
R
y
/n
2
k
B
T
e
)
(9.56)
This is identical to the expression found for bremsstrahlung emissivity (9.54) with
¯g(ω, T
e
) replaced by the factor in the square bracket provided
¯
hω>Z
2
R
y
/n
2
;if
this is not satisfied the Gaunt factor g
n
≡ 0. In other words recombination radiation
only contributes to the plasma emissivity for photon energies greater than the
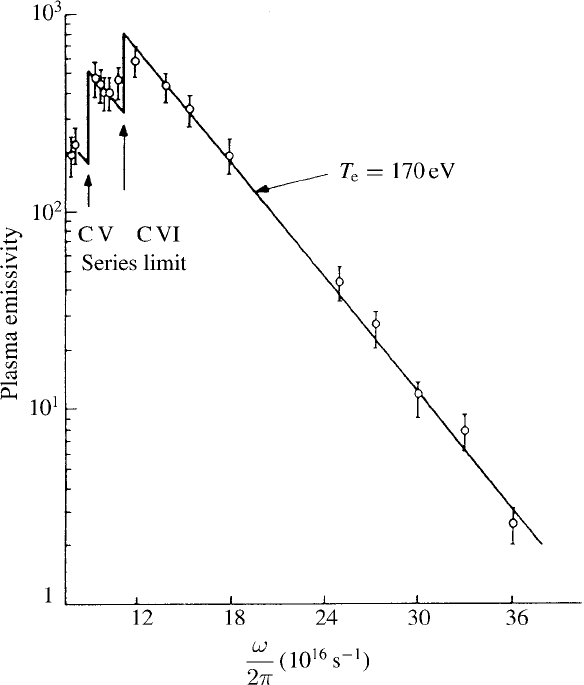
9.4 Plasma bremsstrahlung 341
Fig. 9.6. Plasma emissivity showing contributions from recombination radiation super-
posed on the bremsstrahlung spectrum as a function of photon frequency (after Galanti
and Peacock (1975)).
ionization energy of the quantum state involved. This is seen in the characteristic
step at the recombination edge,
¯
hω = Z
2
R
y
/n
2
(see Fig. 9.6).
9.4.4 Inverse bremsstrahlung: free–free absorption
The process inverse to bremsstrahlung, free–free absorption, occurs when a photon
is absorbed by an electron in the continuum. Its macroscopic equivalent is the
collisional damping of electromagnetic waves (see Exercise 6.4). For a plasma in
local thermal equlibrium, having found the bremsstrahlung emission (9.54), we
may then appeal to Kirchhoff’s law to find the free–free absorption coefficient α
ω
.

342 Plasma radiation
In the Rayleigh–Jeans limit this gives
α
ω
(T
e
) =
64π
4
3
√
3
Z
2
n
e
n
i
m
3
cω
2
e
2
4πε
0
3
m
2πk
B
T
e
3/2
¯g(ω, T
e
) (9.57)
where ¯g(ω, T
e
) is defined by (9.49). It is instructive to note that the parametric
dependences in this expression for inverse bremsstrahlung may be retrieved from
a quite different approach. If we return to the result of Exercise 6.4 expressing the
collisional damping of electromagnetic waves and use this to obtain the absorption
coefficient we recover (9.57) with the Coulomb logarithm in place of the Maxwell-
averaged Gaunt factor, a difference that reflects the distinction between these sepa-
rate approaches. Whereas inverse bremsstrahlung is identified with incoherent ab-
sorption of photons by thermal electrons, the result in Exercise 6.4 is macroscopic
in that it derives from a transport coefficient, namely the plasma conductivity. At
the macroscopic level, electron momentum is driven by an electromagnetic field
before being dissipated by means of collisions with ions.
Absorption of radiation by inverse bremsstrahlung as expressed by (9.57) is most
effective at high densities, low electron temperature and for low frequencies. The
mechanism is important for the efficient absorption of laser light by plasmas. We
expect absorption to be strongest in the region of the critical density n
c
, since this is
the highest density to which incident light can penetrate. In the neighbourhood of
the critical density Zn
e
n
i
∼ n
2
c
= (mε
0
/e
2
)
2
ω
4
L
, where ω
L
denotes the frequency
of the laser light, so that free–free absorption is sensitive to the wavelength of the
incident laser light.
9.4.5 Plasma corrections to bremsstrahlung
Up to now we have ignored plasma effects in discussing bremsstrahlung emission
and its transport through the plasma. To deal with the second issue we need to
refer to our discussion of radiative transport in Section 9.3 where plasma dielectric
effects were allowed for. For an isotropic plasma the emission coefficient (9.48) is
valid only for frequencies ω ω
p
and otherwise needs to be corrected when the
refractive index is no longer approximately unity. This in turn amounts to aban-
doning the particle model for a full kinetic theory formulation of wave propagation
which is beyond the scope of this discussion.
The bremsstrahlung emission described by (9.48) was determined on the basis of
binary encounters between electrons and ions. However as we saw in Section 8.4,
collisions in plasmas are predominantly many-body rather than binary. For fre-
quencies around ω
p
there is time for an electron cloud to screen the positive ion
so that an electron no longer feels a simple Coulomb field. This suggests that
the cut-off in the Gaunt factor introduced in Section 9.4.1 should be taken as
9.4 Plasma bremsstrahlung 343
b
max
∼ λ
D
, the Debye length. However as we have seen already, bremsstrahlung
emissivity is not especially sensitive to the choices made for the impact parameter
cut-off.
For frequencies close to ω
p
it is no longer correct to neglect correlations between
electrons. Dawson and Oberman (1962) showed that the correction to the Gaunt
factor in the region ω ω
p
due to Langmuir wave generation was insignificant
for a plasma in thermal equilibrium. However for non-thermal plasmas, emission
in the neighbourhood of the plasma frequency may be many orders greater than
thermal levels. A brief account of one aspect of radiation by Langmuir waves is
given in Section 11.6.
9.4.6 Bremsstrahlung as plasma diagnostic
Bremsstrahlung emissivity through its dependence on electron temperature, plasma
density and atomic number clearly has potential as a plasma diagnostic. In the first
place the exponential dependence in (9.54) means that for
¯
hω ≥ k
B
T
e
the slope
of a log-linear plot of the bremsstrahlung emissivity provides a direct measure
of T
e
. Next, the strong dependence of the emission on the atomic number of
the plasma ions in principle allows the impurity content in a hydrogen plasma
to be determined. Moreover, if the plasma electron temperature is known in-
dependently, the level of bremsstrahlung could be used to estimate the plasma
density.
In practice the picture is less clear. Even for thermal plasmas, for which
bremsstrahlung losses do not result in significant modification of the distribution
function, unfolding the electron temperature from the bremsstrahlung spectrum is
not as straightforward as might first appear. Limited spectral resolution may result
in the true slope being masked by recombination edge effects or suffering distortion
from discrete lines in the spectrum. Bremsstrahlung from a tokamak plasma with
a modest content of high Z impurities such as nickel and molybdenum, will be
affected by contributions from these impurities.
Moreover, the assumption of a Maxwellian or near-Maxwellian electron dis-
tribution may not be justified. Since the temperature is deduced from the X-
ray spectrum in the region
¯
hω/k
B
T
e
> 1, any non-Maxwellian component will
lead to errors in the measurements. Non-Maxwellian electron distributions in
both space and laboratory plasmas are commonplace. It may happen for exam-
ple that a Maxwellian distribution that describes the bulk electrons is modified
by a high-energy tail of suprathermal electrons. Even though the population of
suprathermals is only a fraction of that of the bulk electrons, they may nevertheless
exercise an influence on the overall electron dynamics disproportionate to their
numbers.

344 Plasma radiation
9.5 Electron cyclotron radiation
We consider next radiation by an electron moving in a uniform, static magnetic
field. For electron energies no more than moderately relativistic, radiation is emit-
ted principally at the cyclotron frequency with contributions at low harmonics
of this frequency and is generally referred to as cyclotron radiation. Emission
from highly relativistic electrons differs in that higher harmonics now contribute
significantly to the spectrum and the harmonic structure is smoothed on account of
harmonic overlap. In this limit the emission is referred to as synchrotron radiation.
We discuss the two limits separately.
In solving for the motion of a charged particle in a static uniform magnetic field
B
0
in Chapter 2 we neglected radiation, so that the total energy of the particle was
a constant of the motion. We shall assume – and later justify – that the energy is
effectively constant, that is, the energy radiated per complete orbit is negligible
compared with E = [m
2
c
4
+ p
2
c
2
]
1/2
, where m is the rest mass and p the electron
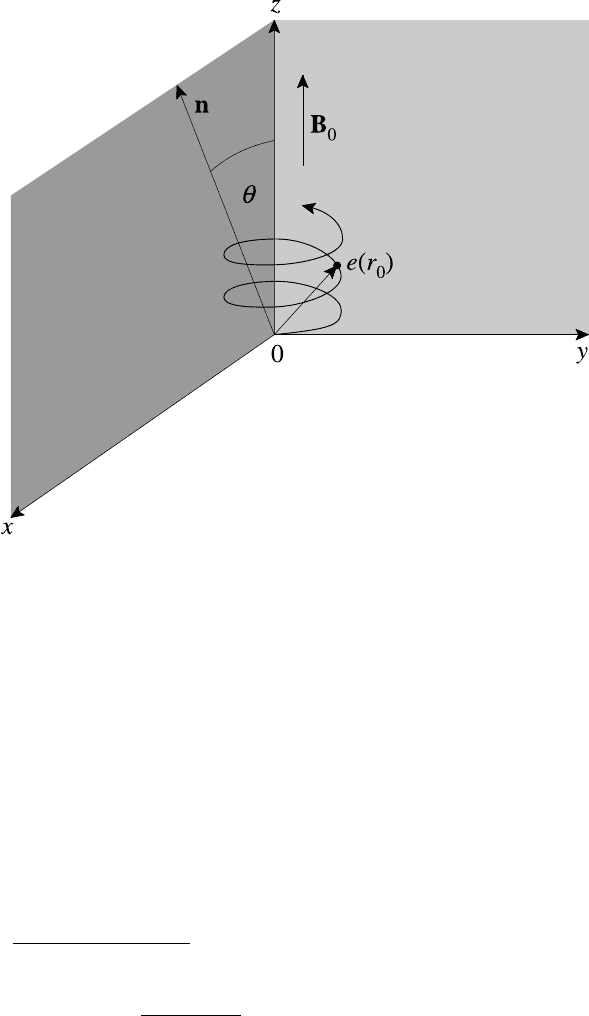
momentum. We saw from Section 2.2 that the solution to the Lorentz equation
corresponds to a helical trajectory, with the axis of the helix parallel to B
0
as in
Fig. 9.7. If we now take the z-axis as the path of the guiding centre and set α = 0,
the electron velocity v and trajectory r
0
are
v =
ˆ
xv
⊥
cos t −
ˆ
yv
⊥
sin t +
ˆ
zv
r
0
=
ˆ
x(v
⊥
/)sin t +
ˆ
y(v
⊥
/)cos t +
ˆ
zv
t
(9.58)
where
= eB
0
/γ m =
0
/γ (9.59)
is the relativistic Larmor frequency. Our task is then to use (9.58) in (9.26) to
calculate the power radiated by an electron per unit solid angle per unit frequency
interval. If we suppose the axes are oriented so that radiation is detected by an ob-
server in the Oxz plane then n = (sin θ,0, cos θ). The steps involved are outlined
in Exercise 9.6.
The expression found for the cyclotron power radiated by an electron is then
d
2
P
d dω
=
e
2
ω
2
8π
2
ε
0
c
∞
l=1
cos θ − β
sin θ
2
J
2
l
(x) + β
2
⊥
J
2
l
(x)
× δ(l − ω[1 −β
cos θ]) (9.60)
where x = (ω/)β
⊥
sin θ and the J
l
denote Bessel functions of the first kind. The
spectrum of the emitted radiation consists of lines at frequencies
ω
l
=
l
1 − β
cos θ
=
l
0
(1 − β
2
⊥
− β
2
)
1/2
1 − β
cos θ
(9.61)
The emission lines are shifted from the cyclotron resonances on two accounts, a
9.5 Electron cyclotron radiation 345
Fig. 9.7. Source–observer geometry for electron radiating in a uniform magnetic field.
relativistic shift from the numerator and a Doppler shift from the denominator.
For weakly relativistic electron energies, the Doppler shift is dominant other than
for angles θ → π/2. A point to bear in mind is that (9.60) expresses the rate of
emission at the source; to obtain the power seen by an observer we have to multiply
(9.60) by (1 − β
cos θ)
−1
.
The total power P
l
in a given harmonic line l follows on integrating over all
directions. This is best done by transforming to the guiding centre frame and then
using a Lorentz transformation to find the radiated power in the laboratory frame.
The procedure is outlined in Exercise 9.7, the result being
P
l
=
e
2
2
0
(1 − β
2
)
2πε
0
cβ
⊥
(1 − β
2
)
3/2
×
lβ
2
⊥
J
2l
2lβ
⊥
(1 − β
2
)
1/2
−l
2
(1 − β
2
)
β
⊥
/(1−β
2
)
1/2
0
J
2l
(2lt) dt
(9.62)
This result has an interesting history and was first found by Schott (1912) determin-
ing the power radiated by a ring of n electrons. Schott’s results were subsequently
346 Plasma radiation
rediscovered decades later in descriptions of synchrotron radiation from particle
accelerators.
The expression for P
l
simplifies considerably in the weakly relativistic limit. We
shall see in the following section that provided lβ 1, P
l+1
/P
l
∼ β
2
⊥
so that the
intensities of the harmonics fall off rapidly with increasing harmonic number so
that almost all of the radiation is emitted in the fundamental, or cyclotron emission
line, and in low (l = 2, 3,...)harmonics.
9.5.1 Plasma cyclotron emissivity
In the weakly relativistic limit electron cyclotron emission (ECE) has potential as a
diagnostic. To explore this we first need to find the plasma cyclotron emissivity by
averaging the power radiated over the electron distribution function, f (β
⊥
,β
).On
the assumption that the electrons are uncorrelated, the plasma cyclotron emissivity
l
(ω), defined as the rate of emission of cyclotron radiation in the harmonic line l
per unit volume of plasma per unit solid angle, is given by
l
(ω) = 2πc
3
d
2
P
d dω
f (β
⊥
,β
)β
⊥
dβ
⊥
dβ
(9.63)
with d
2
P/d dω defined by (9.60). In the weakly relativistic limit, with lβ 1 and
using the small argument approximation for the Bessel function, J
l
(x) ∼ (x/2)
l
/l!
in (9.60), (9.63) reduces to
l
(ω, θ ) =
e
2
c
2
ω
2
2πε
0
l
2l
[l!]
2
(cos
2
θ + 1) sin
2(l−1)
θ
×
∞
0
∞
−∞
β
⊥
2
2l+1
f (β
⊥
,β
)δ(l − ω[1 −β
cos θ])dβ
⊥
dβ
(9.64)
For a Maxwellian distribution function integration over velocity space gives
l
(ω, θ ) =
ne
2
l
2
2
16π
2
ε
0
c
l
2l
[l!]
2
(cos
2
θ + 1) sin
2(l−1)
θ
×
3
k
B
T
e
2mc
2
l
mc
2
2πk
B
T
e
1/2
(ω
l
cos θ)
−1
exp
−
mc
2
2k
B
T
e
(ω − ω
l
)
2
ω
2
l
cos
2
θ
(
(9.65)
where ω
l
is defined by (9.61). In contrast to bremsstrahlung, cyclotron radiation
appears as a line spectrum so that the question of line broadening is critical to
determining line profiles.
We see from this expression for the plasma cyclotron emissivity that the emission
is anisotropic, in that the observed intensity depends on the direction of the detector
relative to the source, and consists of a fundamental at the electron cyclotron
