Boyd T.J.M., Sanderson J.J. The Physics of Plasmas

Подождите немного. Документ загружается.

8.4 Fokker–Planck equation 307

that is τ

<

3/2

. In the collisional (or Pﬁrsch–Schl

uter) regime we have

||

−1

 τ

<τ

and it follows that there is an intermediate regime in which

<τ

/

3/2

. This is the most difﬁcult regime to analyse but, as one can

see from the ﬁgure, the perpendicular diffusion coefﬁcient has the same order of

magnitude at either end of the interval 

3/2

<ν

< 1 and hence this is known as

the plateau regime.

8.4 Fokker–Planck equation

The BGK model for the collision term in (8.1), while useful for the sort of cal-

culation carried out in Section 8.2, is too simple to give a realistic representation

of collisional effects in quantitative calculations. It does not, for example, conserve

particle number, momentum or energy. Also, as already noted, it assumes that there

is a given collision frequency so we cannot use the model to discover the properties

(e.g. parametric dependence) of collision frequencies. We must, therefore, turn to

more sophisticated models.

At ﬁrst, plasma physicists used the well-known Boltzmann collision integral for

(∂ f /∂t)

even though it was recognized that logically this was an unsatisfactory

way to proceed. The Boltzmann derivation assumes short range, binary collisions

whereas in a plasma there may be typically a thousand particles in the Debye

sphere, all of which are interacting with each other simultaneously so that collisions

are characteristically long range (compared with the mean interparticle separation)

and many-body. Most of these collisions are ‘weak’ in the sense that the potential

energy of the interaction (∼ e

/λ

) is very much less than the mean thermal energy

(∼ k

T ) and it can easily be shown (see Exercise 8.4) that the cumulative effect

of the many weak collisions far outweighs the effect of the rare strong interactions

for which e

/r ∼ k

T , that is r/λ

∼ (nλ

)

−1

 1.

In these circumstances, akin to those met in Brownian motion, the Fokker–

Planck approach is more appropriate. Here, one supposes that a function ψ(v,v)

may be deﬁned such that ψ is the probability that a particle with velocity v acquires

a small increment v in a time t. It then follows that

f (r, v, t) =



f (r, v − v, t − t)ψ(v −v,v)d(v) (8.22)

since this equation simply states that we arive at f (r, v, t) by ‘summing over’ all

possible increments v which were likely to occur t seconds earlier. Note that

ψ(v,v) is assumed independent of t, i.e. the collisional process has no ‘memory’

of earlier collisions; a process having this property is said to be Markovian. This is

discussed further in Section 12.6.2.

308 Collisional kinetic theory

Since the ‘increments’ v are small the integral in (8.22) may be expanded to

give

f (r, v, t) =



d(v)



f (r, v, t − t)ψ(v,v) − v ·

∂

∂v

( f ψ)

vv :

∂

( f ψ)

∂v∂v

+···



(8.23)

Clearly, the total probability of all possible deﬂections must be unity:



ψ d(v) = 1

Then, deﬁning the rate of change of f due to collisions by



∂ f

∂t



f (r, v, t) − f (r, v, t − t)

t

we ﬁnd from (8.23)



∂ f

∂t



=−

∂

∂v



f v

t



∂

∂v∂v



f vv

t



(8.24)

where



v

vv





ψ(v,v)



v

vv



d(v)

are the average changes in v and vv in time t. It is important to note here

that both of these average changes are proportional to t whereas third and higher

order terms in the Taylor expansion in (8.23) are of higher order in t and have,

therefore, been dropped. The reason why vv is of the same order in t as

v is that collisions are treated as a random walk process in which mean square

displacements increase linearly with time.

Substitution of (8.24) in (8.1) gives the Fokker–Planck equation. Until we deﬁne

the probability function ψ(v,v), however, it remains a formal statement. Various

forms of the Fokker–Planck equation have been derived for a plasma including

attempts to describe many-particle collisions in terms of rapidly oscillating electric

ﬁelds (Gasiorowicz, Neuman and Riddell (1956)) and charge density ﬂuctuations

(Kaufman (1960)). We shall follow the derivation of Rosenbluth, MacDonald and

Judd (1957) who, using heuristic arguments like those of Landau (1946), assumed

that multiple collisions could be treated as sequences of binary collisions and

calculated v/t and vv/t on the basis of the dynamics of Coulomb

collisions.

8.4 Fokker–Planck equation 309

We consider collisions between a particle of mass m with initial velocity v and

a ‘scattering’ particle of mass m

and initial velocity v

. It is convenient to work in

the centre of mass frame of reference and deﬁne the initial relative velocity

g = v − v

and the centre of mass velocity

V =

mv + m

m + m

We ignore the effect of any macroscopic forces over the duration of a collision on

the assumption that they act over length scales much greater than the Debye length.

Then, denoting ﬁnal velocities by primed variables, we may write

v = V +

m + m



= V



m + m



and conservation of momentum and energy gives

V = V



|g|=|g



Thus,

v = v



− v =

m + m



− g) =

m + m

g (8.25)

Now if the differential scattering cross-section is σ(|g|,θ)then the probability in

time t of collisions with scattering angle θ is proportional to tf

)|g|σ(|g|,θ),

where f

is the distribution function of scattering particles, and so the average value

of v is given by

v=t



d f

)|g|σ(|g|,θ)v

m + m

t



d f

)|g|σ(|g|,θ)g (8.26)

where the integration is over the solid angle  and all scattering velocities v

With reference to Fig. 8.4 we see that all particles passing through the element

of area 2πb db are scattered into the element of solid angle d = 2π sin θ dθ and

so the differential scattering cross-section

σ(|g|,θ)=−

2πb db

d

=−

b db

sin θ dθ

where the minus sign is introduced to make σ a positive quantity since db/dθ is

negative. The fundamental relationship between the impact parameter b and the

scattering angle θ for Coulomb interactions is (see Goldstein (1959))

b = b

cot θ/2 (8.27)

310 Collisional kinetic theory

Fig. 8.4. Scattering in centre of mass frame.

Fig. 8.5. Resolution of g



where

(m + m

)

4πε

|g|

is the impact parameter for right-angle scattering and z, z

are the atomic numbers†

of the scattered and scattering particles, respectively.

† We use lower case z here since we want to allow for z = Z (ions) and z =−1 (electrons).

8.4 Fokker–Planck equation 311

To carry out the integration over solid angle we ﬁrst resolve g



into its com-

ponents in a rectangular coordinate system with polar axis parallel to g. This is

illustrated in Fig. 8.5 and leads to the result

g = g



− g = g[sin θ cos φ e

+ sin θ sin φ e

+ (cos θ − 1) e

]

On integration over the azimuthal angle φ, components perpendicular to g vanish

(scattering is equally likely in all perpendicular directions) and one ﬁnds

v

t

=−





m + m





) dv

(8.28)

where the sum is over all types of scattering particles and we have assumed

 =

4πε

ln(λ

) ≈

4πε

ln 

where ln  is the Coulomb logarithm. In deriving this result we have applied a cut-

off at small scattering angles corresponding to θ

min

= 2b

/λ

which is equivalent

to a maximum impact parameter b

max

= λ

, as can be seen from (8.27) in the limit

of small θ . Strictly speaking, this means that  should have a subscript s, indeed

is a function of v

, but since this dependence lies entirely inside the argument of

the logarithm it is customary to ignore it. Thus, we substitute the plasma  for

, and treat  as a constant. In evaluating vv only the cross terms in

gg now vanish on integration over φ. However, since weak collisions (small

θ) dominate, the e

term, which is of order θ

(compared with the e

and e

terms which are of order θ

) turns out to be smaller by a factor ln(λ

) and we

neglect it with the result

v

v



t

= 





− g

) dv

(8.29)

Noting that

=−

∂

∂v





(8.30)

and

− g

∂

∂v

(8.31)

we may express the Fokker–Planck coefﬁcients in terms of the Rosenbluth poten-

tials deﬁned by

G(v) =





|v − v

| f

) dv

(8.32)

312 Collisional kinetic theory

and

H(v) =





m + m





)

|v − v

(8.33)

From (8.28) and (8.30) we have

v

t

= 

∂ H

∂v

and from (8.29) and (8.31)

v

v



t

= 

∂

∂v

which, on substitution in (8.24), gives



∂ f

∂t



=−

∂

∂v



∂ H

∂v





∂

∂v∂v



∂

∂v∂v



(8.34)

This is the usual form of the Fokker–Planck collision term. As we shall see in

the next section, the ﬁrst term in (8.34) produces a deceleration of a test particle

and is known as the coefﬁcient of dynamical friction. The second term accounts for

the spreading of a unidirectional beam throughout velocity space and is called the

coefﬁcient of diffusion. A complication of the Fokker–Planck coefﬁcients is their

non-linear dependence on the distribution function f which appears explicitly and

implicitly in the Rosenbluth potentials. An approximation frequently made is to use

Maxwell distributions in the Rosenbluth potentials though this is really justiﬁed

only for near-equilibrium plasmas.

Another interesting and useful form of the Fokker–Planck collision term is ob-

tained (see Exercise 8.5) by noting that

∂

∂v



∂

∂v∂v



=−

∂

∂v



∂

∂v∂v



(8.35)

Substituting this expression for g/g

in (8.28) and integrating by parts with respect

to v

we obtain



∂ f

∂t



m

∂

∂v





∂

|v − v

∂v∂v



)

∂ f (v)

∂v

−

f (v)

∂ f

)

∂v



(8.36)

It can be shown (see Hinton (1983)) that the Fokker–Planck equation has the

following desirable properties:

• the distribution function cannot become negative – collisions act to ﬁll holes in

velocity space;

• particle number, momentum and energy are conserved;

8.5 Collisional parameters 313

• it satisﬁes Boltzmann’s H-theorem, i.e. the only time-independent distribution

functions satisfying (∂ f /∂t)

= 0 are Maxwellians.

8.5 Collisional parameters

By taking velocity moments of the Fokker–Planck equation we may deﬁne and

ﬁnd estimates for various collisional parameters. The sort of parameters of interest

are the time scales for an arbitrary distribution of velocities to become Maxwellian

and for the equalization of ion and electron temperatures. A very simple model that

permits the calculation of rough estimates of such time scales is the test particle

model in which a single test particle (either an electron or an ion) travels through a

uniform, ﬁeld-free plasma in thermal equilibrium. Then the Fokker–Planck equa-

tion is simply

∂ f

∂t

=−

∂

∂v



∂ H

∂v





∂

∂v∂v



∂

∂v∂v



(8.37)

Its moments give expressions for the rates of change of velocity, energy, etc. and the

distribution functions are simple enough for the collision moments to be evaluated.

The distribution function of the test particle is

f (v, t) = δ[v − V(t)] (8.38)

where V(t) is the particle velocity at time t and we ﬁnd estimates for various col-

lisional parameters by evaluating the velocity moments at t = 0. A more rigorous

approach is presented by Hinton (1983) but the results are the same.

Multiplying (8.37) by v and integrating gives

∂V

∂t

= 

∂ H(V)

∂V

(8.39)

where the term in G has vanished on integration by parts twice. This conﬁrms the

statement in the previous section that the ﬁrst Fokker–Planck coefﬁcient represents

the dynamical friction decelerating the test particle.

Since the plasma particles, the scatterers, are assumed to be in thermal equilib-

rium

) = f

) =

3/2

−a

(8.40)

where

and it follows that

H(v) =





m + m



φ(a

v) (8.41)

314 Collisional kinetic theory

where φ(x) is the error function

φ(x) =

√



−y

Noting that H (v) is an isotropic function (a direct consequence of assuming f

be isotropic) it follows that (8.39) may be written

∂V

∂t

= 

∂ H(V )

∂V

=−ν

(V )V

say, deﬁning the frictional coefﬁcient ν

. Hence,

2





m + m



(a

V ) (8.42)

where

(x) =

φ(x) − xφ



(x)

The ﬁrst observation from (8.42) is that, for given V , ν

decreases as the plasma

density decreases or its temperature increases; in other words, collisions are less

effective under low density, high temperature conditions. Also, using the limiting

values

φ(x) → 2x/

√

π(x) → 2x/3

√

π as x → 0

φ → 1 (x) → 1/2x

as x →∞



(8.43)

we see that for very fast test particles (a

V →∞)ν

∝ V

−3

, while in the opposite

limit (a

V → 0), where V is much less than the thermal speeds, ν

is independent

of V . Thus, the frictional deceleration of a test particle increases with V at low

speeds but decreases with V at sufﬁciently high speeds. A consequence of this is

that the current in a plasma tends to be carried predominantly by the electrons in

the tail of the velocity distribution.

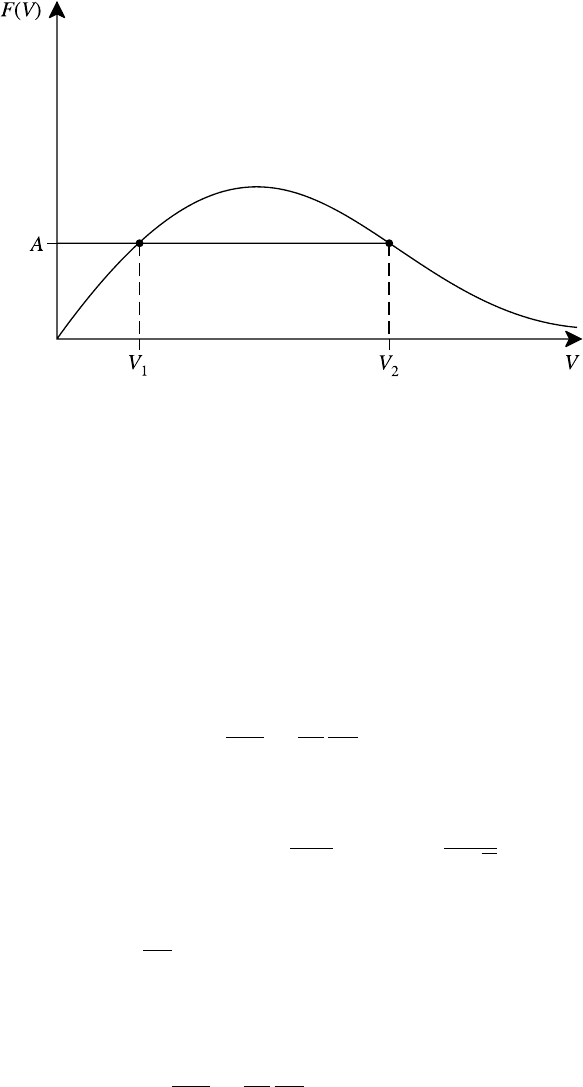
Another possible consequence is a phenomenon known as electron runaway.If

one imagines an electron subjected to a constant accelerating force then a balance

will be achieved at low velocities but not at those velocities for which the frictional

force is less than the accelerating force and decreasing. The situation is represented

schematically in Fig. 8.6 where A is the acceleration and F(V ) = ν

(V )V is

the frictional deceleration. The equilibrium point at V

is stable but that at V

unstable and an electron with V > V

is continually accelerated. In practice this

is likely to be limited by instabilities, such as the two-stream instability, driven by

the free energy in the runaway electrons.

Although the frictional coefﬁcient is an important parameter for such matters as

the slowing down of particle beams, collision frequencies, representing all manner

8.5 Collisional parameters 315

Fig. 8.6. Schematic illustration of electron runaway.

of collisional effects, must be deﬁned more generally. By convention the collision

frequency is taken to be the inverse of the mean time for a particle to be deﬂected

through a right-angle. To ﬁnd a measure of this using the test particle model we take

the v

⊥

moment of (8.37) where v

⊥

is the sum of the squares of the components of

v perpendicular to V(0); it is necessary to use a mean square deviation since, in an

isotropic plasma, the mean deviation is zero. Here we ﬁnd (see Exercise 8.6) that

only the second term in (8.37) gives a non-zero contribution (as predicted in the

previous section) which may be written as

∂V

⊥

∂t

2

∂G

∂V

(8.44)

Substituting (8.40) in (8.32) gives

G(v) =







v +



φ(a

v) +

−a

√



(8.45)

and

∂G

∂v



[φ(a

v) − (a

v)] (8.46)

It is convenient to deﬁne separate collision frequencies for the scatterers so we

write (8.44) as

∂V

⊥

∂t

2

∂G

∂V



316 Collisional kinetic theory

and using (8.46) we have

(V ) =

2

[φ(a

V ) − (a

V )] (8.47)

This parameter gives a measure of the time scale for relaxation to isotropy of an

initially anisotropic distribution which is perhaps the chief reason for its adoption

as the collision frequency. Using the asymptotic expansions (8.43) we see that ν

∝

−2

for a

V → 0andν

∝ V

−3

for a

V →∞.

It is of particular interest to compare electron–electron, ion–ion, electron–ion

and ion–electron collision frequencies which we label ν

, where a indicates the

scattered (test) particle and b the scattering particles. From (8.47) we ﬁnd

ln 

2πε

[φ(a

V ) − (a

V )]

ln 

2πε

[φ(a

V ) − (a

V )]

ln 

2πε

[φ(a

V ) − (a

V )]

ln 

2πε

[φ(a

V ) − (a

V )]

where Ze is the ionic charge so that n

= Zn

. To estimate relaxation times we

take the test particle speed V to be thermal in which case the terms in square

brackets in ν

and ν

become constants of order one but for ν

and ν

we must

take respectively the large and small argument limits in (8.43) with the result

: ν

∼ 1:Z





1/2





3/2

: Z : Z







Except when Z or T

is large, it is the mass ratio which dominates this com-

parison of collision frequencies and we see that ν

∼ Z ν

 ν

.The

ﬁrst of these gross inequalities arises because thermal ion speeds are less than

thermal electron speeds, by (m

)

1/2

if T

≈ T

, and so ions take longer to meet

each other. The second reﬂects the fact that the electrons are not very effective in

deﬂecting the much heavier ions.

Another set of useful collision parameters is obtained by considering the energy

exchange between the test particle and the scatterers. Here again we use a mean

square deviation to deﬁne the parameters because the test particle is both losing

energy due to its deceleration in the forward direction and gaining energy in the

perpendicular direction by its deﬂection. If W is the energy of the test particle,

W = m[v

− V

(0)]/2 and we take the (W )

moment of (8.37). Denoting this