Boyd T.J.M., Sanderson J.J. The Physics of Plasmas

Подождите немного. Документ загружается.

8.2 Simple transport coefﬁcients 297

In fact, the development of plasma transport theory has proved to be one of

the most challenging problems in plasma physics. In this chapter our aim is to

do no more than give a short introduction to the topic by means of basic physical

arguments and approximate mathematical models. It is preferable to begin with this

admittedly oversimpliﬁed transport theory and so, for the moment, we continue to

beg the question as to what is the collision frequency. Later on in the chapter, using

a more sophisticated model for the collision term in (8.1), we derive parametric

expressions for various collision frequencies and thereby identify which frequency

is appropriate for each transport process.

8.2 Simple transport coefﬁcients

In the equation relating a ﬂux to the thermodynamic force driving the ﬂux, the con-

stant of proportionality is called the transport coefﬁcient. For example, in Fourier’s

law

q =−κ∇T

relating the heat ﬂux q to the temperature gradient ∇T , the constant of propor-

tionality κ is called the coefﬁcient of thermal conductivity. Our aim is to derive

from (8.1) expressions for the most important transport coefﬁcients. We do this

by adopting a very simple model for the collision term, (∂ f/∂t)

, and then taking

velocity moments of the equation to obtain the relationships between various ﬂuxes

and their thermodynamic forces. The model simulates the effect of close binary

collisions where particles experience sudden, local velocity changes and so its

application to plasmas, strictly speaking, ought to be limited to the Lorentz gas

model, which assumes that the electrons scatter off inﬁnitely heavy, stationary ions.

Suppose that a plasma, initially in thermal equilibrium, is disturbed by various

external perturbations giving rise to small, steady state ﬂuxes of matter, momentum

or energy. Since collisions drive the distribution function towards a Maxwellian on

a time scale of order ν

−1

, the simplest representation of the collision term in the

kinetic equation is



∂ f

∂t



=−ν

( f − f

) (8.2)

where f

is a local Maxwellian given in general by

(r, v) = n(r)



2πk

T (r)



3/2

exp

−m[v − u(r)]

/2k

T (r)

(8.3)

In (8.2), known after Bhatnagar, Gross and Krook (1954) as the BGK model, ν

is a constant, which we shall subsequently identify with an appropriate collision

frequency, and ( f − f

) is, of course, the difference between the actual value of

298 Collisional kinetic theory

the distribution function and the local Maxwellian. The BGK model supposes that

collisions act in such a way as to decrease f where it is greater than f

and increase

f where it is less than f

at a rate which is proportional to | f − f

|. The method

assumes all perturbations and perturbing forces are small and solves the linearized

kinetic equation. Also, as simple a version of (8.3) is used as is consistent with

the description of the transport process under consideration. We wish to derive

expressions valid for both ions and electrons but to avoid cluttered notation we

suppress the species label and write the particle charge as Ze, where Z =−1for

electrons.

As a ﬁrst example let us ﬁnd an expression for the electrical conductivity σ .

Here a uniform plasma may be assumed and we may take the unperturbed plasma

to be at rest so that f

is the Maxwell distribution

= f

≡ n



2πk



3/2

−mv

/2k

(8.4)

The plasma is then subjected to a weak electric ﬁeld E which is both constant and

uniform. This perturbs the plasma so that f = f

+ f

and the linearized kinetic

equation is

ZeE

∂ f

∂v

=−ν

(8.5)

Since

σ E = j = Ze



v f dv = Ze



v f

dv (8.6)

it follows from (8.5), on multiplying by Zev and integrating over velocity space,

that

j =

E ·



vv f

dv (8.7)

Taking E to deﬁne the x direction, j

and j

are zero and we ﬁnd from (8.6) and

(8.7)

σ =

mν

(8.8)

The electrical conductivity is the current per unit electric ﬁeld. The mobility of a

particle, µ

, is deﬁned as its velocity per unit ﬁeld and hence

nZe

mν

(8.9)

8.2 Simple transport coefﬁcients 299

Next consider the diffusion coefﬁcient D. This is deﬁned as the particle ﬂux

caused by unit density gradient. Here, assuming uniform temperature, we may take

= n(r)



2πk



3/2

−mv

/2k

so that with no external forces the linearized kinetic equation is

v ·

∂ f

∂r

v ·

∂n

∂r

=−ν

(8.10)

Since the particle ﬂux 



 =



v f dv, we ﬁnd on multipling (8.10) by v and integrat-

ing over velocity space



 =−

nν



v f

v · ∇n dv =−

mν

∇n

and hence

D =

mν

(8.11)

From (8.9) and (8.11)

(8.12)

which is known as the Einstein relation.

The thermal conductivity κ is usually deﬁned for constant pressure so that, since

p = nk

T (8.13)

one must allow both n and T to be inhomogeneous and take

= n(r)



2πk

T (r)



3/2

exp[−mv

/2k

T (r)]

Then the steady state, force-free kinetic equation gives, using (8.13),

v ·

∂T

∂r



−



=−ν

(8.14)

The heat ﬂux q is given by

q =



v f dv =



v f

so that multiplication of (8.14) by

v and integration over velocity space gives

q =



vv · ∇Tf

dv −



vv · ∇Tf

=−

5nk

∇T

300 Collisional kinetic theory

Hence the thermal conductivity

κ =

5nk

2mν

The coefﬁcient of viscosity µ is deﬁned as the shear stress produced by unit

velocity gradient. Taking the local ﬂow velocity u in the x direction and its gradient

in the z direction we may write

= n



2πk



3/2

exp



−

[(v

− u(z))

+ v

]



and substitution in the kinetic equation gives

− u) f

=−ν

(8.15)

From the deﬁnition of µ

=−



m(v

− u)v

f dv =−m



− u)v

dv (8.16)

Thus, multiplying (8.15) by m(v

− u)v

and integrating gives, using (8.16),

µ = nk

T/ν

Note that there is no explicit mass dependence in this result. A consequence of

this is that the viscosity of a plasma is determined by the ions since, as we shall see

in Section 8.5, the ion collision frequency is smaller than that of the electrons by

the square-root of the mass ratio. For all the other transport coefﬁcients calculated

so far, this consideration is outweighed by the explicit appearance of the particle

mass in the denominator so that the electrons dominate these transport processes.

8.2.1 Ambipolar diffusion

So far we have investigated transport under the simplest possible conditions. To

complete this discussion we examine some important practical considerations. For

example, in the presence of a density gradient the diffusion of electrons and ions

will occur in general at different rates. When particle temperatures are approxi-

mately equal, the electrons diffuse more rapidly than the ions and if the containing

walls are insulated, a space charge is set up due to the accumulation of excess

electrons near the wall. This has the effect of simultaneously decreasing electron

mobility µ

and increasing ion mobility µ

. The ion and electron ﬂuxes are deter-

mined by



=−D

∇n

+ n



=−D

∇n

+ n



(8.17)

8.2 Simple transport coefﬁcients 301

where E is the ﬁeld due to the space charge. A steady state is reached when j = 0

so that there is no further build-up of space charge. Then Z



= 



= 



, say, and

eliminating E from (8.17), assuming Zn

= n

= n,gives



 =−D

∇n

where the ambipolar diffusion coefﬁcient

− µ

Using the Einstein relation (8.12) and assuming T

= T

this becomes

(Z + 1)D

+ D

≈ (Z + 1)D

since D

 ZD

. Thus, the resultant ambipolar diffusion is determined by the

slower ion rate.

In the steady state the ﬁeld set up by the space charge is, from (8.17),

E =

− D

)

(µ

− µ

)

∇n

≈−

∇n (8.18)

Since

∇ · E =

(Zn

− n

) (8.19)

the quasi-neutrality condition Zn

≈ n

implies from (8.18) and (8.19) that

− n

∼





 1

where L is the length scale of the boundary layer over which the ﬁeld and density

gradients exist. Thus, quasi-neutrality is established within a few Debye lengths of

the insulating wall; this deﬁnes the sheath thickness.

8.2.2 Diffusion in a magnetic ﬁeld

Finally, let us consider diffusion in a magnetized plasma. For a plasma in a steady

state with no electric ﬁeld we have from the kinetic equation

v ·

∂ f

∂r

(v × B) ·

∂ f

∂v

=−ν

which becomes on linearization

v ·

∂ f

∂r

(v × B

) ·

∂ f

∂v

=−ν

(8.20)

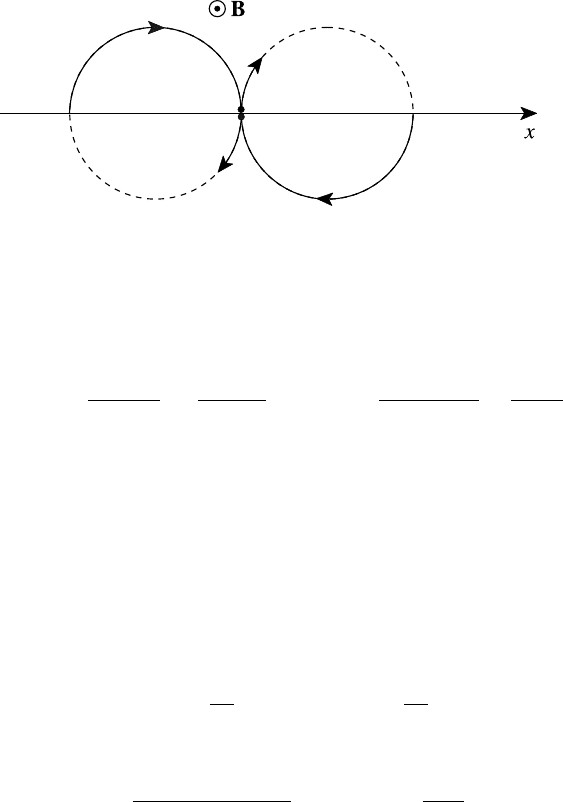
302 Collisional kinetic theory

Fig. 8.1. Collisional diffusion in a strong magnetic ﬁeld.

If we suppose that B

is in the z direction and the density gradient is in the z and x

directions, then we choose f

to be the bi-Maxwellian distribution

= n(x, z)



2πk

⊥



2πk





1/2

exp

−

m(v

+ v

)

⊥

−



(

since a plasma may have, in general, different parallel and perpendicular tempera-

tures. The v

,andv

moments of (8.20) give

⊥

/m)(∂n/∂x) − 

=−ν





=−ν





/m)(∂n/∂z) =−ν









(8.21)

where  = ZeB/m is the cyclotron frequency.

Deﬁning D

⊥

and D





=−D

⊥

∂n

∂x



=−D



∂n

∂z

we ﬁnd from (8.21)

⊥

mν

[1 + (/ν

)

]



mν

showing that diffusion along the magnetic ﬁeld is unaffected by the ﬁeld, while

diffusion across the ﬁeld is reduced by the factor (1 + (/ν

)

−1

In the limit (/ν

)

→ 0, we recover, as expected, the unmagnetized result for

⊥

= k

⊥

/mν

= λ

, where λ

is the collisional mean free path for motion

across the ﬁeld. In the opposite limit D

⊥

≈ k

⊥

/m

= r

, where r

is the

Larmor radius. Thus, the Larmor radius replaces the mean free path as the length

scale for diffusion but the time scale is still the collision time.

This is explained in Fig. 8.1 which shows the effect of collisions on gyrating

particles. For simplicity, a head-on collision is considered between particles with

equal speeds as a result of which the particles exchange orbits allowing each to

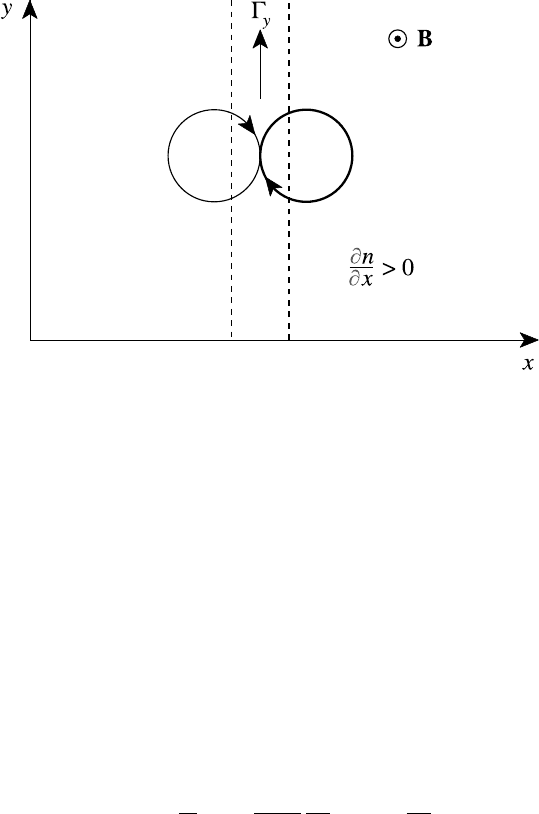
8.2 Simple transport coefﬁcients 303

Fig. 8.2. Gyro-magnetic particle ﬂux.

progress in opposite directions along the x-axis. In the absence of a density gradient

there would, of course, be no net ﬂux but, for ∂n/∂ x > 0, there are more particles

travelling to the left than to the right and hence there is a net ﬂux down the density

gradient. Since the ﬂux in the x direction is entirely dependent upon collisions and

particles describe their Larmor orbits in search of a collision partner, it follows that

the diffusion length scale is now determined by the Larmor radius rather than the

collisional mean free path.

Note that there is a ﬂux in the y direction as well,



=−





D

⊥

∂n

∂x

→ r



∂n

∂x

in the limit (/ν

)

→∞. This gyro-magnetic ﬂux is the dominant ﬂux in this

limit and is independent of the collision frequency! Applying the argument used

in Fig. 8.1 to collisions occurring along the y-axis yields no net ﬂux because there

is no density gradient in this direction. On the other hand, in a thin sheet in the

yz-plane there are more particles to the right than to the left so that contributions

to 

from particles whose Larmor orbits intersect the sheet do not cancel out,

as demonstrated in Fig. 8.2. Collisions play no part in this ﬂux which is entirely

gyro-magnetic.

304 Collisional kinetic theory

8.3 Neoclassical transport

The model used in the preceding section to calculate transport coefﬁcients avoids

various complications and interdependences. Nevertheless, for collisional plasma

transport in a uniform magnetic ﬁeld, generally referred to as classical transport,

it gives the correct parametric dependence. However, the magnetic ﬁelds needed

for toroidal conﬁnement are both curved and inhomogeneous so it is essential to

see what modiﬁcations to classical transport theory are needed as a result. This

development of the theory is known as neoclassical transport.

As for classical transport, a rigorous treatment requires solution of the kinetic

equations and is very complicated. However, order of magnitude expressions can

be obtained by simple heuristic arguments beginning with the expressions obtained

for diffusion in a uniform magnetic ﬁeld. Diffusion coefﬁcients have dimensions of

(length)

/time and for D



, where the magnetic ﬁeld has no effect, we have shown

that



= λ

/τ

since the collisional mean free path λ

= V

and τ

is the interval between

collisions. On the other hand D

⊥

, for the strong ﬁeld case ||ν

, is expressed

⊥

= r

/τ

Each of these results may be interpreted in terms of a random walk model of

diffusion. For parallel diffusion the particle travels, on average, a distance λ

be-

fore a collision randomly alters its direction, the average interval for such random

changes being τ

. The time interval is the same for perpendicular diffusion since

it is still collisions which cause the random realignments but particles restricted to

Larmor orbits cannot travel a mean free path in the perpendicular direction and so

must be replaced by r

This simple picture changes fundamentally once the ﬁeld becomes inhomoge-

neous because particle guiding centres are no longer attached to ﬁeld lines but

drift across them. The Larmor orbits are of no signiﬁcance in this case since the

perpendicular migration is determined by the guiding centre motion. To ﬁnd the

appropriate length scale for perpendicular diffusion we need to consider the global

geometry of the ﬁeld. In a toroidal plasma, as we know from the discussion in

Section 4.3.2, the ﬁeld lines turn in the poloidal direction as they wind around

the torus so that one ‘cycle’, deﬁned by the line returning to its starting point,

is completed after travelling a distance qR, where q is the safety factor and R

is the (major) radial coordinate of the guiding centre. According to the random

walk model the time for the particle guiding centre to travel this distance is

8.3 Neoclassical transport 305

given by

t = (qR)



= (qR)

assuming parallel diffusion is collisional. During this time the guiding centre mi-

grates in the perpendicular direction a distance of order v

t, where v

is the drift

speed, and

col

⊥





/τ

In general, the actual drift velocity, being the resultant of both grad B and curvature

drifts, is given, in order of magnitude, by

∼

||R

and hence

col

⊥

≈ q

/τ

Typically, the safety factor q ∼ 3 so this is an order of magnitude greater than for

a uniform ﬁeld.

This result is valid provided qR >λ

for we have assumed that diffusion in

the parallel direction is collisional. In fact, it is frequently the case that qR <λ

and then a further modiﬁcation is needed. Because the particles migrate across the

poloidal cross-section they are subject to a varying toroidal ﬁeld given by

B =

+r cos θ

≈ B

(1 −  cos θ)

where R

is the major radius, B

the ﬁeld strength on the minor axis and  = r/R

the inverse aspect ratio, assumed to be small. It follows that those particles with

small enough v



may be reﬂected by the magnetic mirror effect. Such particles are

trapped in the banana-shaped orbits discussed in Section 2.10 where it was shown

that these particles have velocities satisfying the condition



(0)|/v

⊥

(0) ≤ (2)

1/2

If n

is the number density of such particles, for an isotropic velocity distribution,

∝



(0)

⊥

(0)

∝ 

1/2

is small. However, the effect on diffusion is signiﬁcant because v



is also small and

so the time for the trapped particles to traverse the orbit is correspondingly long, as

is the resultant perpendicular migration.

306 Collisional kinetic theory

Fig. 8.3. Variation of perpendicular diffusion coefﬁcient with collision frequency.

Repeating the random walk calculation for the perpendicular diffusion of the

trapped particles we now have a length scale given by









||R





1/2





1/2

||

where τ

= (qR/V

) is the bounce time. The particle will remain trapped in the

banana orbit until it is scattered out of the trapped velocity band by collisions.

We shall show in Section 8.5 that the effective collision frequency for vanishingly

small velocity V varies as V

−2

and hence the effective collision time in this case is

eff

= τ

Bearing in mind that only a fraction ∝ 

1/2

of the particles are trapped in banana

orbits, it follows that the effective diffusion coefﬁcient across the ﬁeld lines is given

ban

⊥

= 

1/2





1/2





/τ



3/2

which is a factor 

−3/2

greater than that obtained for untrapped (or passing) parti-

cles. This represents a further order of magnitude increase over the uniform ﬁeld

result for typical aspect ratios.

These results are represented in Fig. 8.3 which shows schematically the variation

of the perpendicular diffusion coefﬁcient with collision frequency ν

= τ

−1

.At

lowest collision frequencies we are in the banana regime for which τ

eff

>τ

/

1/2