Boyd T.J.M., Sanderson J.J. The Physics of Plasmas
Подождите немного. Документ загружается.


7.3 Landau damping 267
and has an asymptotic series representation
Z(ζ ) =−
1
ζ
1 +
1
2ζ
2
+
3
4ζ
4
+···
+ is
√
πe
−ζ
2
(7.41)
with
s =
0 ζ>0
1 ζ = 0
2 ζ<0
and a power series representation
Z(ζ ) = is
√
πe
−ζ
2
− 2ζ
1 −
2
3
ζ
2
+
4
15
ζ
4
−···
(7.42)
The dispersion relation may be represented in terms of the plasma dispersion func-
tion as
2k
2
λ
2
D
= Z
(ω/
√
2kV
e
) +
Z
a
T
e
T
i
Z
(ω/
√
2kV
i
) (7.43)
where Z
a
is the ion atomic number. Assuming V
i
ω/k V
e
it follows that
ζ
e
≡ (ω/
√
2 kV
e
) 1 while ζ
i
≡ (ω/
√
2 kV
i
) 1, which allows us to use
the power series representation (7.42) for Z(ω/
√
2kV
e
) and the asymptotic series
representation (7.41) for Z(ω/
√
2kV
i
) to write an approximate dispersion relation
2k
2
λ
2
D
+ [2 + 2i
√
πζ
e
] − Z
a
T
e
T
i
1
ζ
2
i
+
3
2ζ
4
i
− 2i
√
πζ
i
e
−ζ
2
i
= 0 (7.44)
The real part of (7.44) reproduces the fluid dispersion relation (6.98), i.e.
ω
2
r
k
2
=
Z
a
k
B
T
e
/m
i
(1 + k
2
λ
2
D
)
+
3k
B
T
i
m
i
(7.45)
The imaginary part of (7.44) determines the Landau damping of the ion acoustic
mode which is approximately
γ
ω
pi
−
π
8
1/2
ω
r
ω
pi
1
(1 + k
2
λ
2
D
)
3/2
m
e
m
i
1/2
+
T
e
T
i
3/2
exp
−
T
e
/2T
i
1 + k
2
λ
2
D
−
3
2
(7.46)
The terms in square brackets denote electron and ion Landau damping, respec-
tively. Expressed in this form we see that for T
e
/T
i
1, ion Landau damping
can be neglected compared with the electron contribution. However, in practice
this condition is rarely satisfied sufficiently strongly so that both contributions
are needed. Moreover, though (7.46) is useful in that it shows the parametric
dependence of both electron and ion contributions, to get an accurate picture of the
damping it is necessary to solve complex dispersion relations numerically. Results
of a numerical solution of (7.43) are shown in Fig. 7.7.
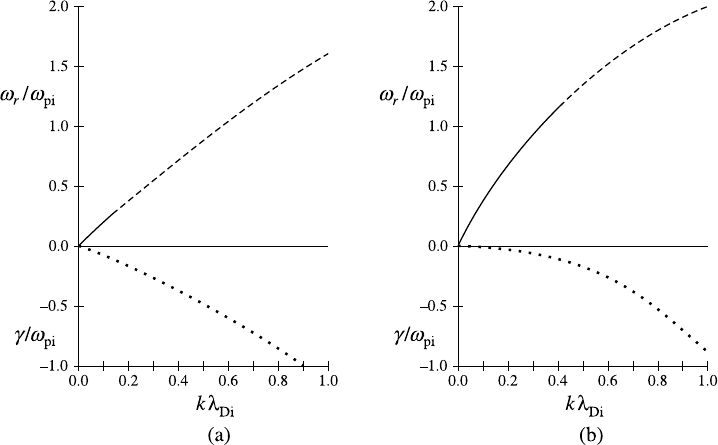
268 Collisionless kinetic theory
Fig. 7.7. The real part of the frequency and the damping rate (dots) for an ion acoustic wave
as functions of wavenumber for a hydrogen plasma with (a) T
e
/T
i
= 1, (b) T
e
/T
i
= 10.
Dashed lines indicate that the wave is heavily Landau damped.
7.4 Micro-instabilities
Fluid instabilities are macroscopic in the sense that their growth depends on cer-
tain fluid parameters and if growth occurs it involves all of the plasma within
some region in which the relevant parameters have the appropriate values. Micro-
instabilities, on the other hand, are driven by the interaction of a wave with only
a relatively small fraction of the particle population, namely those that are in
resonance with the wave. The instability is ‘localized’ in velocity (v) space rather
than in coordinate (r) space. Even within a fluid element not all of the particles are
directly involved in the instability and so there is no bulk motion of the plasma such
as one sees with fluid instabilities. Nevertheless, micro-instabilities can have sig-
nificant effects on the properties of a plasma. For example, the enhanced fluctuation
levels of naturally occurring, or externally excited, waves may alter the transport
properties of the plasma giving rise to anomalous or turbulent (wave–particle)
transport rather than classical (collisional) transport.
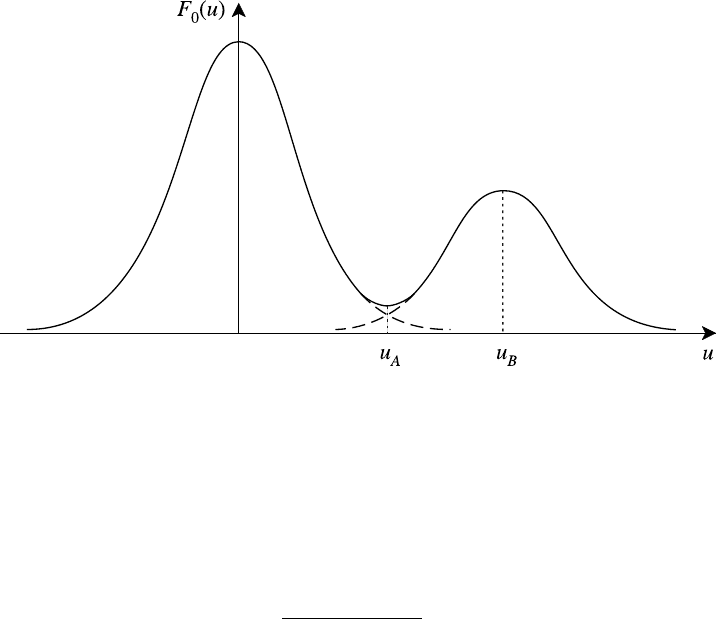
The simplest example of a micro-instability is the so-called ‘bump-on-tail’ in-
stability (BTI). Instead of the single-humped Maxwellian F
0
(u) that we considered
in the last section we suppose that a few of the electrons have been removed from
the main body of the plasma and re-inserted as a small flux of hot particles out in
the tail of the distribution as shown in Fig. 7.8. If we carry out the same analysis
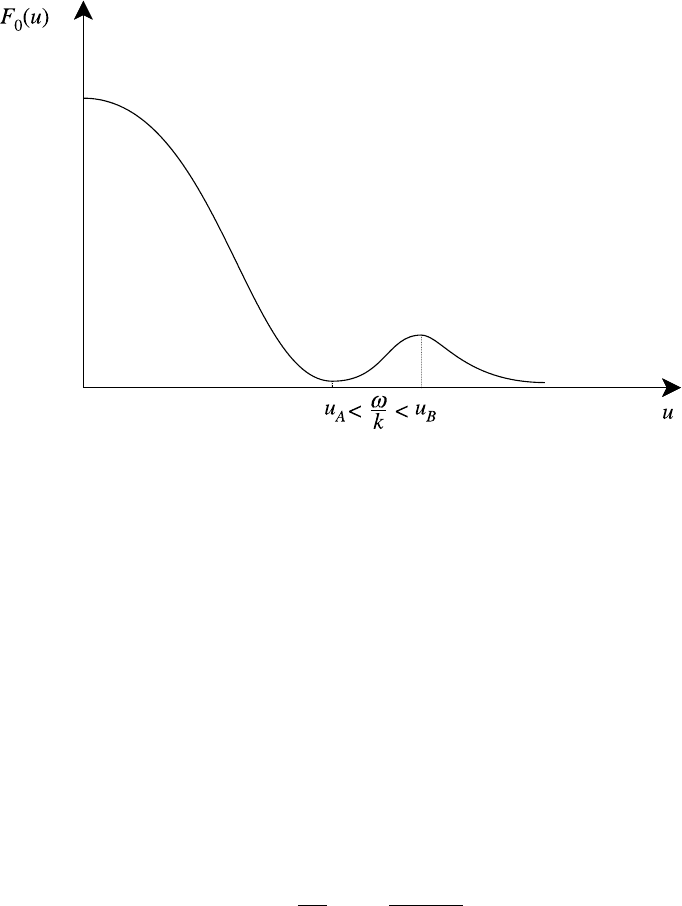
7.4 Micro-instabilities 269
Fig. 7.8. Bump-on-tail distribution function.
that led to Landau damping we would expect that p would still be given by (7.34)
since the small bump would have no significant effect on the integral in (7.32)
but, of course, p = γ would change sign for waves with phase velocities lying
between u
A
and u
B
because dF
0
/du > 0 between these limits.
It might be thought that whenever the distribution function F
0
(u) has a range of
values of u for which dF
0
/du > 0 some waves will grow and the equilibrium will
be unstable. However, that would overlook the simplifying assumption made to
obtain the results (7.34) and (7.37), namely, that k → 0, in which case |γ ||p|.
In general, the equilibrium is unstable if there is a solution of (7.27) for which
p > 0 (see Fig. 7.1). Now there is a powerful theorem in complex analysis which
provides a method of determining this. Taking k as real and positive and re-writing
(7.27) as
D(V ) = 1 −
ω
2
pe
k
2
+∞
−∞
F
0
(u)du
u − V
= 0 (7.47)
where V = (ω
r
+iγ)/k, we wish to know whether there are any values of V which
satisfy this equation and for which γ/k > 0. The argument principle tells us that
if we draw any closed contour C in the complex V -plane and trace its image C
D
in
the complex D-plane then the number of zeros minus the number of poles of D(V )
inside C is equal to the number of times C
D
encircles the origin in the D-plane.
The contour C that we wish to investigate is shown in Fig. 7.9. As R →∞this
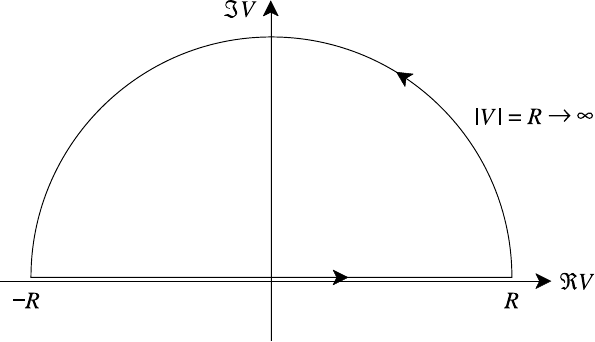
270 Collisionless kinetic theory
Fig. 7.9. Semi-circular contour of integration in upper half-plane.
encompasses the whole of the upper half-plane, in which V > 0, i.e. γ>0. Now,
by its definition, D(V ) is analytic in the upper half-plane so it has no poles and the
argument principle simply tells us how many zeros of D(V ) there are.
The image contours C
D
in the D-plane are called Nyquist diagrams, examples
of which are shown in Fig. 7.10. Figure 7.10(a) shows schematically what the
C
D
contour might look like for the stable case of F
0
(u) given by the Maxwell
distribution. In the limit of R →∞the semi-circle, |V |→∞, maps on to the
point D = 1 as we can easily see from (7.47). For the rest of the contour, i.e.
−∞ < V < +∞, (7.35) may be used to evaluate the integral in (7.47) from
which we see that there is only one other point where D = 0 and that is at V = 0
where dF
0
/du = 0. At this point the second term in (7.47) is positive and so D > 1.
Also, on the contour, D has the same sign as V so that the curve is traced in the
manner shown. This contour does not encircle the origin confirming that there are
no zeros of (7.47) in the upper half V -plane.
Figures 7.10(b),(c) show possible contours C
D
for a double-humped distribution
where there are now three values of V for which D = 0. For the bump-on-tail
distribution (see Fig. 7.8) these are V = 0, u
A
, u
B
. Figure 7.10(b) corresponds to a
stable double-humped distribution because C
D
still does not encircle the origin. On
the other hand, in Fig. 7.10(c) the origin is encircled once so there is an unstable
root of the dispersion relation (7.47).
Penrose (1960) showed that there is a simple criterion which can be applied to
determine stability without the need to construct the Nyquist diagram. First we note
that, if there is to be an unstable root, C
D
must cross the D-axis in the left-half
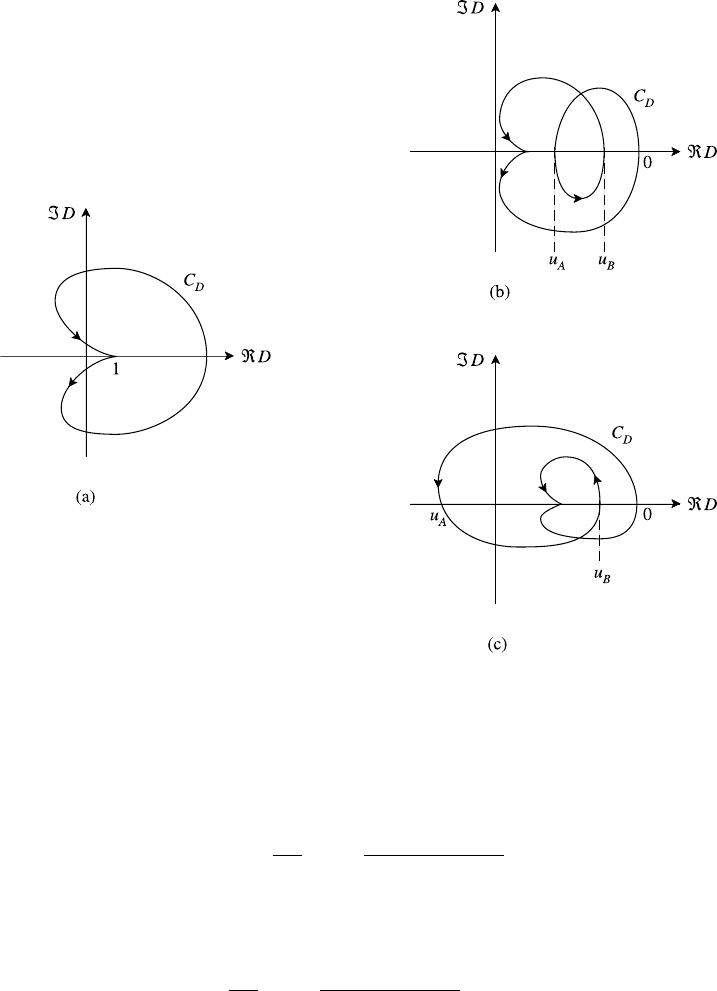
7.4 Micro-instabilities 271
Fig. 7.10. Nyquist diagrams for (a) stable Maxwellian, (b) stable and (c) unstable double-
humped distributions.
plane, that is D(u
A
)<0. Using (7.35) and noting that dF
0
(u
A
)/du = 0†
D(u
A
) = 1 −
ω
2
pe
k
2
+∞
−∞
F
0
(u) − F
0
(u
A
)
u − u
A
du < 0
On integration by parts this becomes
1 −
ω
2
pe
k
2
+∞
−∞
F
0
(u) − F
0
(u
A
)
(u − u
A
)
2
du < 0 (7.48)
† Note that since both numerator and denominator vanish at u = u
A
we do not need to take the principal part
of the integral.
272 Collisionless kinetic theory
Fig. 7.11. Beam–plasma distribution function.
But since k can vary from 0 to ∞ there will be some value of k for which (7.48) is
satisfied provided only that
+∞
−∞
F
0
(u) − F
0
(u
A
)
(u − u
A
)
2
du > 0 (7.49)
This is a necessary and sufficient condition for instability and is known as the
Penrose criterion. Near u = u
A
the integrand in (7.49) is approximately equal to
F
(u
A
), which is positive since F(u
A
) is a minimum. However, the existence of
a minimum is not, of itself, a sufficient condition for instability since all particles
interact with the wave, giving or taking energy depending upon their relative phase.
In effect, the Penrose criterion says that the minimum must be deep enough that
the net effect of the givers outweighs that of the takers.
If u
B
is sufficiently large then the hot electron beam becomes completely sepa-
rated in velocity space from the main distribution function and rather than a ‘bump-
on-tail’ instability we have a beam–plasma instability. In this case, illustrated in
Fig. 7.11, F
0
(u
A
) → 0 and so (7.49) is certainly satisfied (F
0
(u)>0 for all u)
but since all the beam electrons now contribute to the instability, it is no longer
a resonant, micro-instability but a macroscopic instability. It ought, therefore, to
be describable by the fluid equations. The link between the two is explored in the
following section.
7.4 Micro-instabilities 273
7.4.1 Kinetic beam–plasma and bump-on-tail instabilities
In Section 6.5 we found the characteristics of the two-stream instability (TSI) and
the beam–plasma instability (BPI) from a cold fluid model. In both cases instability
was caused by a feedback that produced charge bunching, with one system reacting
back on the other. However, there are other cases in which only nearly resonant par-
ticles in the distribution are involved and which consequently cannot be described
by a fluid model, since one is not then able to identify separate systems. Resonant
instabilities have to be described using kinetic theory. Instabilities often exist in
both reactive and resonant forms. For example, the bump-on-tail instability (BTI)
is the kinetic counterpart of the reactive BPI. To explore the relation between the
two we look again at BPI characteristics, this time from a kinetic standpoint. With
the beam electrons described by the distribution function
f (v) =
n
b
(2π)
3/2
V
3
b
exp
−
(v − v
b
)
2
2V
2
b
where n
b
, v
b
, V
b
denote density, streaming and thermal velocities of the beam
particles, it is straightforward to recover (6.120) in the cold plasma limit. For
the reactive instability, γ
max
∼ (n
b
/n
0
)
1/3
ω
p
. The physical effect of a finite beam
electron temperature is to produce a spread of the beam electron velocities about
v
b
with consequent reduction of the BPI growth rate and ultimate suppression of
the instability. Thermal effects may be ignored provided |ω − k · v
b
|
√
2 kV
b
.
With k ω
p
/v
b
this reduces to
n
b
n
0
1/3
V
b
v
b
(7.50)
For the BTI with v
b
V
b
we see by comparison with Fig. 7.8 that growth
occurs in the region over which the slope of the distribution function is positive,
when ω/k is within the range v
b
− V
b
<ω/k <v
b
. The maximum growth rate is
|γ
max
|
π
2e
1/2
n
b
n
0
v
b
V
b
2
ω
p
(7.51)
in which e = exp(1). The bandwidth ω across which growth is optimal is such
that ω ∼ kV
b
and hence
ω
ω
p
V
b
v
b
(7.52)
Thus the growth rate is less than the bandwidth for optimal BTI growth provided
n
b
n
0
1/3
≤
V
b
v
b
(7.53)
274 Collisionless kinetic theory
Fig. 7.12. Ion and electron distribution functions in a current-carrying plasma subject to
(a) ion acoustic instability and (b) Buneman instability.
The conditions (7.50), (7.53) serve to distinguish the reactive BPI from its kinetic
counterpart.
7.4.2 Ion acoustic instability in a current-carrying plasma
By allowing electrons to drift relative to ions so that the plasma is now current-
carrying, we introduce a source of free energy which will counter Landau damp-
ing and, if strong enough, may drive the mode unstable. Before analysing this
ion acoustic drift instability in terms of the dispersion relation, it is easy to see
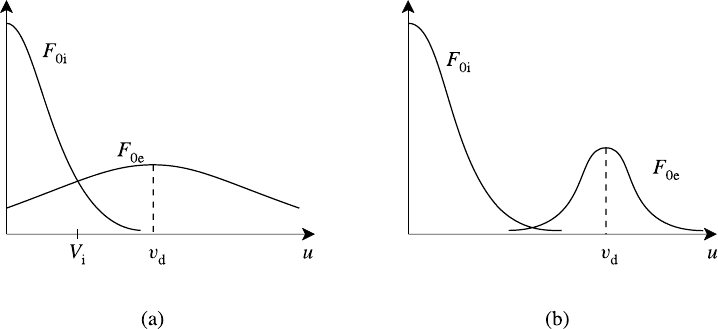
qualitatively how instability arises from a picture of the distribution functions.
Representing the current by a net drift velocity v
d
between ions and electrons,
for the velocity component parallel to the current the distribution functions are
as shown in Fig. 7.12(a). Provided v
d
V
i
there is a range of phase veloci-
ties (V
i
c
s
<v
d
) for which ion Landau damping is negligible but Landau
growth takes place (dF
0e
/du > 0) due to interaction with the resonant elec-
trons.
Here again there is a smooth transition from the resonant micro-instability to
the macroscopic, Buneman instability. Either by increasing v
d
or decreasing T
e
we can separate the ion and electron distributions in velocity space as shown in
Fig. 7.12(b), thus strengthening the instability and converting it from resonant to
reactive.
Returning to the dispersion relation (7.43) it is straightforward to modify it to
allow for electrons drifting relative to ions with a drift velocity v
d
. We prescribe an
ordering v
d
V
e
in addition to the requirement that T
e
/T
i
1 so that ion Landau
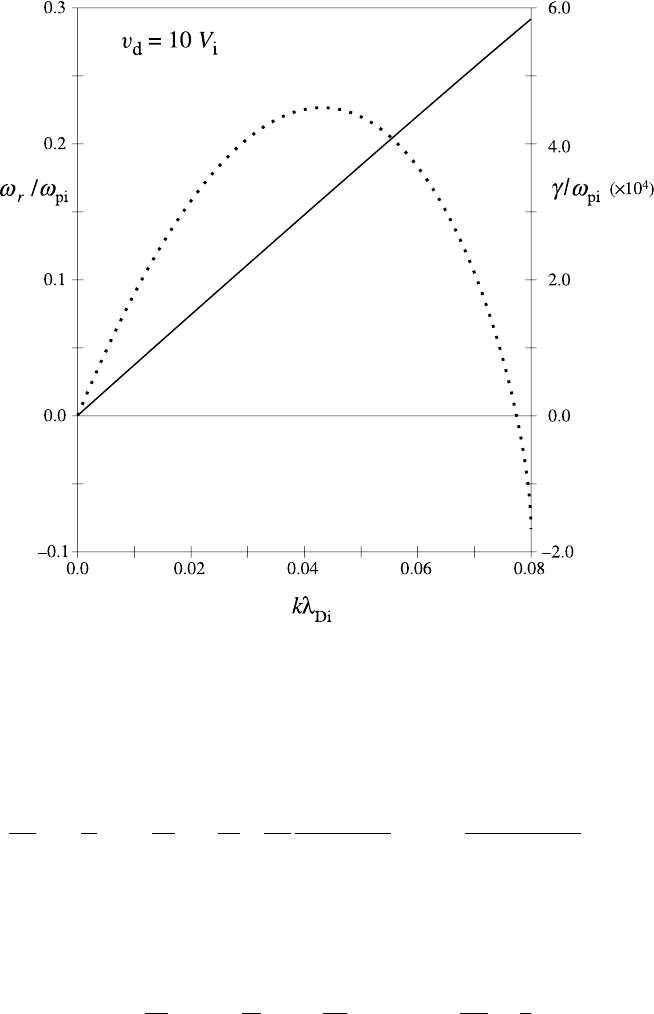
7.4 Micro-instabilities 275
Fig. 7.13. The real part of the frequency and the growth rate (dots) for the current-driven
ion acoustic instability as functions of the wavenumber for a hydrogen plasma with
T
e
/T
i
= 10.
damping can be ignored. It follows that
γ
ω
pi
π
8
1/2
ω
r
k
3
m
i
T
e
1
ω
pi
(kv
d
− ω
r
)
V
e
exp
−
(
ω
r
/k − v
d
)
2
2V
2
e
(7.54)
We see at once that electron drift reduces the electron Landau damping of the mode
and for v
d
> c
s
instability will develop. Instability threshold is determined by (see
Exercise 7.12)
v
d
ω
r
k
1 +
T
e
T
i
3/2
m
i
m
e
1/2
exp
−
T
e
2T
i
−
3
2
which is a sensitive function of the species temperature ratio. Again in practice it
is essential to solve the exact dispersion relation numerically (see Fig. 7.13).

276 Collisionless kinetic theory
7.5 Amplifying waves
In the light of the Landau analysis developed in this chapter we return to the ques-
tion of amplifying waves and convective and absolute instabilities, first discussed
in Section 6.6. In our derivation of Landau damping (and of Landau growth when
a source of free energy is available from a suitable distribution of electrons or ions)
the dispersion characteristics were described in terms of their evolution in time,
i.e. for real values of k, solutions were found for ω ≡ ω(k) with ω complex.
The Landau analysis provided the response in time of the plasma to an initial
perturbation f
1
(x,v,t = 0). Equation (7.25) for the electric field E(k,ω)produced
by the perturbation has the form
E(k,ω) =
g(k,ω)
D(k,ω)
(7.55)
where g(k,ω) is determined by the initial perturbation and D(k,ω), the plasma
dielectric function, is a characteristic of the unperturbed plasma. In Section 7.3
we supposed that the only singularities of E(k,ω) in the complex ω-plane were
poles where D(k,ω) = 0. These complex roots determine the time-asymptotic
behaviour of a perturbation with prescribed (real) k. We now want to turn to other
considerations.
In discussing weakly coupled waves in Chapter 6 we found that conditions under
which amplifying waves were present corresponded to conditions for convective
instability. To determine whether or not a plasma is convectively unstable one
has to examine the evolution of some initial perturbation in both time and space.
The consideration of spatially amplifying waves, on the other hand, is akin to the
Landau analysis of Section 7.3. Here we need to determine the spatial response to
an initial perturbation at some point in the plasma, namely f
1
(x = 0,v,t), rather
than the response in time. This means we now have to allow the wavenumber k
to be complex. We can see at once that this presents a contrast to the Landau case
since clearly the sign of k cannot of itself provide a criterion for distinguishing
amplification on the one hand from attenuation on the other, since a change in the
direction of propagation results in k changing sign.
To determine whether amplification takes place in a plasma we examine the
spatial development of a perturbation at x = 0 oscillating in time,
g(x, t) =
0 t < 0
g
0
δ(x)e
−iω
0
t
t > 0
(7.56)
where g
0
is a constant. The response of the plasma to this perturbation will be
