Boyd T.J.M., Sanderson J.J. The Physics of Plasmas

Подождите немного. Документ загружается.

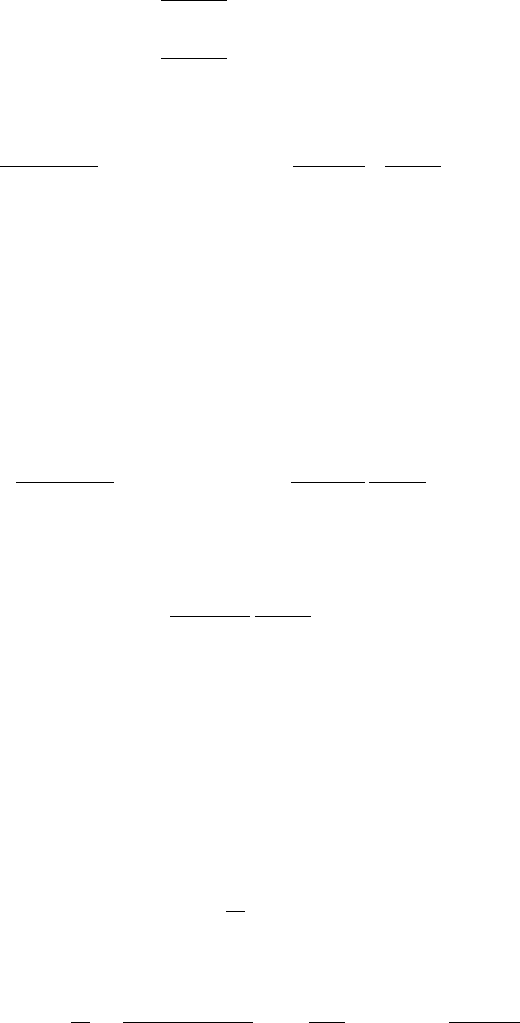
7.3 Landau damping 257

Solving (7.16) by means of Fourier and Laplace transforms, we write

(r, v, t) =

(2π)

3/2



(k, v, t) exp(ik ·r)dk (7.18)

E(r, t) =

(2π)

3/2



E(k, t) exp(ik · r)dk (7.19)

so that (7.16) gives for each Fourier component

∂ f

(k, v, t)

∂t

+ i k · v f

(k, v, t) −

eE(k, t)

∂ f

(v)

∂v

= 0 (7.20)

Before taking the Laplace transform, (7.20) may be simpliﬁed by noting that, since

E is electrostatic,

∇ × E(r, t) = 0

and hence

k × E(k, t) = 0

Thus E(k, t) is parallel to k so that, if u is the component of v along k, (7.20)

becomes

∂ f

(k, v, t)

∂t

+ ikuf

(k, v, t) −

eE(k, t)

∂ f

(v)

∂u

= 0 (7.21)

Taking the Laplace transform of (7.21), that is, multiplying by e

−pt

and integrating

over t from 0 to ∞,weget

( p + iku) f

(k, v, p) −

eE(k, p)

∂ f

(v)

∂u

= f

(k, v, t = 0) (7.22)

where

(k, v, p) =



∞

(k, v, t)e

−pt

dt (7.23)

E(k, p) =



∞

E(k, t)e

−pt

dt (7.24)

From (7.22) f

is obtained as a function of E which we can now substitute in the

Fourier–Laplace transform of (7.17)

ikE(k, p) =−



(k, v, p)dv

to obtain an equation for E alone. Substituting for f

from (7.22)

ikE(k, p) =−



(k, v, t = 0)

p + iku

dv −

E(k, p)



∂ f

/∂u

p + iku

258 Collisionless kinetic theory

Hence

E(k, p) =

kD(k, p)



(k, v, t = 0)

p + iku

dv (7.25)

where

D(k, p) ≡ 1 −



∂ f

/∂u

p + iku

is the plasma dielectric function; note that this is independent of initial conditions.

Carrying out the inverse Laplace and Fourier transforms formally solves the prob-

lem. Unfortunately, this is in general no simple matter. The time dependence of the

kth Fourier component of the electric ﬁeld is given by

E(k, t) =

2πi



σ +i∞

σ −i∞

E(k, p)e

d p (7.26)

where the integration is along a line parallel to the imaginary p-axis and to the

right of all singularities of the integral as indicated in Fig. 7.1(a).

It is a well-known result of complex variable theory that if E(k, p)e

is an an-

alytic function of p except for a ﬁnite number of poles in the inﬁnite strip between

p =−α and p = σ then we may deform the contour of integration to that

shown in Fig. 7.1(b), i.e. we integrate along p =−α instead of p = σ but take

a horizontal detour to go around each of the poles lying between the two vertical

lines. The advantage of this deformation of the contour is that now, on its vertical

section, the integrand decays with time like e

−αt

and vanishes asymptotically. The

integrations along the horizontal lines are taken one in each direction and therefore

cancel out so that we are left with the integrations around the poles which give 2πi

times the sum of the residues at the poles.

For suitable choices of f

and f

(t = 0) (the conditions that ∂ f

/∂u and f

(t =

0) are analytic functions of u are sufﬁcient) the only singularities of E(k, p)e

in the p-plane are simple poles where the dielectric function vanishes. Choosing

= u and deﬁning F

by n

(u) =



(v)dv

, the zeros of D(k, p) are

given by

D(k, p) = 1 −

iω



+∞

−∞

/du

p + iku

du = 0 (7.27)

where ω

= (n

/ε

1/2

is the electron plasma frequency. Thus, if the solutions

of (7.27) are denoted by p

then from (7.26) we get, as t →∞,

E(k, t) =



(7.28)

7.3 Landau damping 259

Fig. 7.1. Deformation of contour of integration in complex p-plane.

where

= lim

p→p

( p − p

)E(k, p)

is the residue of E(k, p) at p

. In general the poles p

are complex, so writing

(k) =−i ω

(k) + γ

(k) (7.29)

260 Collisionless kinetic theory

where ω

and γ

are real, (7.28) becomes

E(k, t) =



−iω

(k)t+γ

(k)t

(7.30)

If any γ

> 0 the ﬁeld grows exponentially and the linear approximation breaks

down, so we shall assume, for the moment, that all poles lie to the left of the

imaginary p-axis. Then all terms with γ

= 0 in (7.30) are exponentially damped

oscillations. Note that none are damped as strongly as e

−αt

; in general we are

interested in the pole closest to the imaginary p-axis since this corresponds to the

smallest damping decrement.

We now investigate the limit of long-wavelength waves, k → 0. To lowest order

in this limit (7.27) gives, on integration by parts and using



du = 1,

p =±i ω

(7.31)

that is, undamped plasma oscillations. To ﬁnd the lowest-order k dependence we

again integrate by parts and expand ( p + iku)

−2

in powers of (iku/ p), giving

−



+∞

−∞

duF

(u)



1 −

2iku

−

+···



= 1 (7.32)

The imaginary term vanishes if F

(u) is isotropic. This is true for all the imaginary

terms in the expansion in (7.32) since they are all odd in u. The ﬁrst correction to

(7.31) arises from the term in k

. Choosing the Maxwell distribution

= n

(m/2π k

)

3/2

exp(−mv

/2k

) (7.33)

it follows that

(u) = (m/2πk

)

1/2

exp(−mu

/2k

)

and from (7.32) we get

p =±i ω



1 +

(kλ

)



(7.34)

It is easily veriﬁed (see Exercise 7.4) that (7.34) corresponds to the dispersion

relation (6.97) for longitudinal electron plasma waves (Langmuir waves) in a warm

plasma.

Since all the imaginary terms vanish in the expansion in powers of k, no damping

appears in such a solution. To ﬁnd the damping decrement one must resort to

the full expression (7.27). This presents a problem since the integrand contains

a pole at u = ip/k which, for pure imaginary p, lies on the path of integration.

However E(k, p) was originally deﬁned on a line in the p-plane to the right of all

singularities, that is, for p > 0 (see Fig. 7.1). Thus, the integral in the u-plane

in (7.27) is also deﬁned for p > 0. This means that the pole at u = ip/k lies

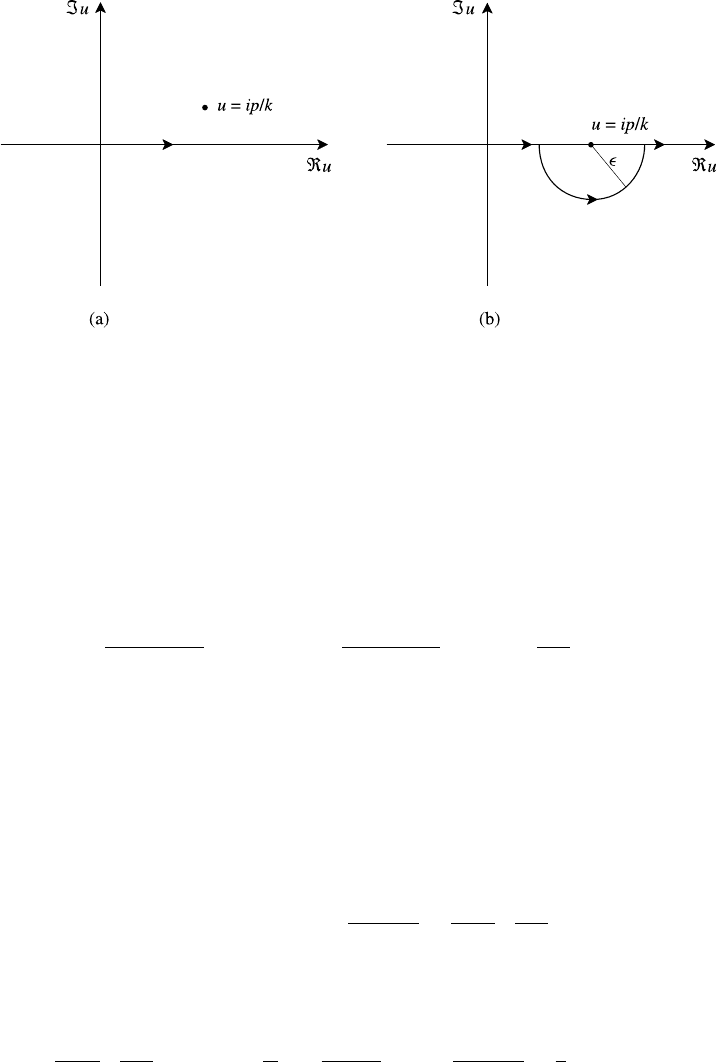
7.3 Landau damping 261

Fig. 7.2. Path of integration along u-axis for pole (a) above axis and (b) on axis.

above the real axis, which is the path of integration in Fig. 7.2(a). In the limit

p → 0 the pole drops on to the real axis but analytic continuation requires that

the path of integration must stay below the pole and so we integrate from −∞ up

to (ip/k) − , then around the semi-circle of radius  below the pole, and ﬁnally

continue along the real axis from (ip/k) +  to +∞ as shown in Fig. 7.2(b). Thus

(7.27) is evaluated by means of the relationship



+∞

−∞

/du

(u − ip/k)

du = P



+∞

−∞

/du

(u − ip/k)

du + iπ





ip/k

(7.35)

where the second term on the right-hand side is simply iπ times the residue of the

integrand at the pole. (Had the pole approached the real axis from below and the

contour been deformed above it, the semi-circle would then have been described

in the negative (clockwise) direction and the sign of this term would be reversed.)

The principal part in (7.35) may be approximated by a power series as in (7.32).

Thus, (7.27) becomes

= (−iω + γ)

=−ω



1 −

iπ p





ip/k



(7.36)

the imaginary part of which gives for the Landau damping decrement

γ =

πω





ip/k

=−





1/2

(kλ

)

exp



−

2(kλ

)

−



(kλ

 1)

(7.37)

262 Collisionless kinetic theory

This result conﬁrms what was said earlier concerning the vanishing of all imaginary

terms in a power series expansion in small k;ask → 0, γ → 0 faster than any

power of k. Numerical solution of (7.27) shows that as kλ

→ 1, |γ |→ω

, that

is, the damping time approaches the period of the oscillations. Thus, the Debye

shielding distance λ

is the minimum wavelength at which longitudinal oscillations

(k  E) can occur. This is easily understood when one notes that at kλ

= 1 the

phase speed of the wave, ω/k, is equal to the mean thermal speed of the electrons.

They are easily able to neutralize the space charge, therefore, and so prevent the

wave from propagating.

A further observation to be made from (7.37) is the following. The damping

decrement arose from the residue at the pole in (7.27). The sign of γ therefore de-

pends critically on the slope of F

(u) at the pole, as is obvious from the ﬁrst equal-

ity in (7.37). Since we considered a Maxwellian, centred at the origin, the slope

was necessarily negative leading to damping. Clearly, the phenomenon of Landau

damping has its physical origin in the interaction of those ‘resonant’ electrons with

u ≈ ω/k. On reﬂection this is not surprising. Since u is that component of electron

velocity in the direction of propagation of the wave, those electrons with u ≈ ω/k

stay roughly in phase with the wave and, therefore, more effectively exchange en-

ergy with it. The actual energy exchange between any particular resonant electron

and the wave depends on the phase of the wave at the position of the electron.

But if a particle with u <ω/k is accelerated then its interaction with the wave is

made more resonant and therefore stronger than if it had been decelerated. Thus,

for particles moving slightly slower than the wave, acceleration is a stronger effect

than deceleration so that, on average, slower particles gain energy from the wave.

Clearly the opposite is true for particles travelling slightly faster than the wave.

Figure 7.3 illustrates the cases of the strongly resonant electrons. A negative slope

to the distribution function at the resonant speed (dF

(u = ω/k)/du < 0) means

that slower particles outnumber faster ones so that the wave loses more energy than

it gains and is therefore damped. It is clear from this argument that kinetic theory

is necessary for a description of Landau damping. Integration (or averaging) over

velocity space which gives rise to a ﬂuid theory removes the physical mechanism,

the microstructure of F

(u), essential for Landau damping. Dawson (1962) de-

veloped the idea of energy exchange between particles and Langmuir waves into a

model from which he was able to retrieve Landau’s result. Nonetheless, misgivings

persisted for a long time as to whether collisionless damping was a real effect.

Had we chosen a distribution function with a range of values of u for which

/du > 0, then for waves with phase velocities in that range we should have

found γ>0 indicating Landau growth rather than damping. Any such unstable

waves are also lost in macroscopic theory and are, therefore, known as micro-

instabilities, some of which we discuss in Section 7.4.

7.3 Landau damping 263

Fig. 7.3. Illustration of interaction of strongly resonant electrons with wave. Filled circles

represent electrons with speed u <ω/k which take energy from the wave. Open circles

represent electrons with speed u >ω/k which give energy to the wave.

7.3.1 Experimental veriﬁcation of Landau damping

Any lingering doubts about the reality of Landau damping were dispelled by deﬁni-

tive experiments by Malmberg and Wharton (1964, 1966) who showed that the

measured spatial attenuation of Langmuir waves agreed remarkably well with Lan-

dau’s result. The appropriate formulation of the Landau problem for comparison

with the measured damping is one in which ω is taken to be real and the dispersion

relation is solved for complex k. In this case we have

k

k

∝ exp



−



In these experiments the plasma was, to a good approximation, collisionless (see

Exercise 7.5). Two probes were used, one of which, the transmitter, was set at a

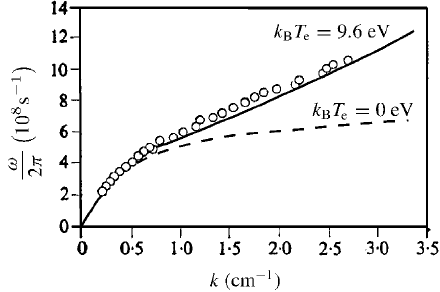
264 Collisionless kinetic theory

Fig. 7.4. Comparison of experimental results (circles) with theoretical dispersion curve for

electron plasma waves. The solid line corresponds to a calculation using the measured tem-

perature while the dashed line is for a cold plasma (after Malmberg and Wharton (1966)).

series of ﬁxed frequencies while the receiving probe, at each setting, was moved

longitudinally. From the data, the real and imaginary parts of the wavenumber

were obtained as functions of frequency. A dispersion plot is shown in Fig. 7.4. In

comparing this result with the theoretical dispersion relation, k = k(ω), Malmberg

and Wharton chose a value of electron density which normalized the theoretical

curve to the experimental data at low frequencies; in this region (high phase veloc-

ities) temperature corrections to the dispersion relation should be negligible. The

measured dispersion plot in Fig. 7.4 shows excellent agreement with theory. Note

however that the theoretical curve is not simply a plot of (7.34); we recall that

(7.34) shows just the leading terms in an asymptotic series. For the conditions in

this experiment, the series is only weakly convergent so that additional terms have

to be retained. Note too that as k → 0,ω → 0 rather than ω

; this departure from

the dispersion relation arises on account of the ﬁnite length of the plasma which

cuts off long wavelengths.

Figure 7.5 shows the measured damping compared with that predicted by theory.

The ordinate is k/k and the abscissa (ω/kV

)

≡ (v

)

where V

is the

electron thermal velocity. The ratio k/k and the phase velocity ω/k are found

directly from experiment. Since the electron velocity distribution was shown to

be Maxwellian, T

was known experimentally. It is clear that in a collisionless

plasma, electron plasma waves suffer exponential damping. The observed damp-

ing lengths range from 0.02 to 0.5 m, very much shorter than the electron mean

free path. The magnitude of this damping, together with its dependence on phase

velocity and on electron temperature, conﬁrms the behaviour predicted for Landau

damping.

7.3 Landau damping 265

Fig. 7.5. Comparison of experimental results with theoretically predicted Landau damping

of electron plasma waves (after Malmberg and Wharton (1966)).

7.3.2 Landau damping of ion acoustic waves

Landau damping is not restricted to Langmuir waves nor is it solely an electron

phenomenon. Any wave with phase velocity close to either of the particle thermal

velocities will suffer Landau damping. Ion acoustic waves with phase velocity c

lying between V

and V

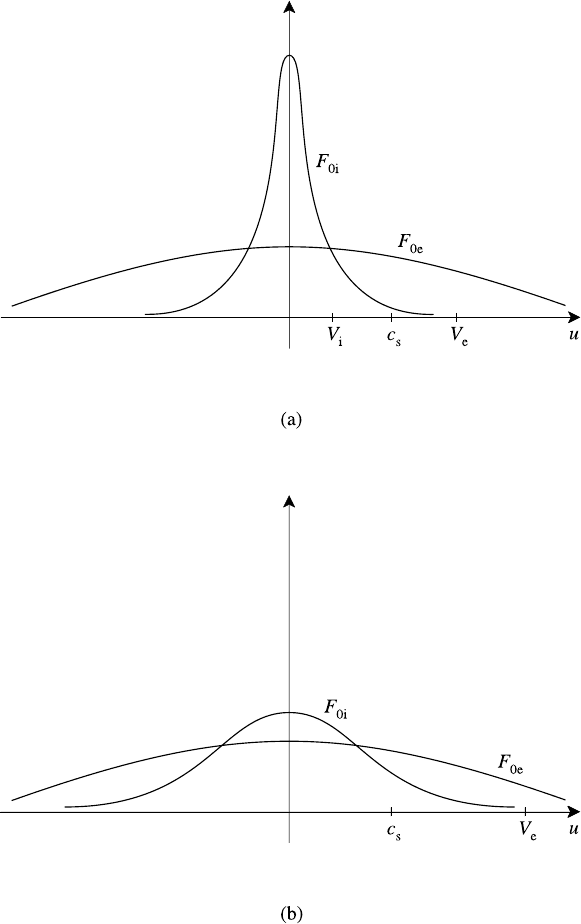
provide a particularly interesting example.

In general, V

 V

so F

(u) is a squeezed version of F

(u) and, for T

 T

Fig. 7.6(a) shows that there is weak Landau damping of the waves due to both ions

and electrons. The damping is weak on the part of the ions because c

 V

and

so there are very few ions in resonance with the wave. On the other hand, electron

Landau damping is weak because c

 V

and so dF

/du ≈ 0atu = c

. For the

case that T

≈ T

, c

∼ V

as shown in Fig. 7.6(b). Now, although electron Landau

damping is still weak, ion damping is strong. In fact a numerical solution of the

kinetic dispersion relation (see Fig. 7.7(a)) shows that |γ |∼ω

To examine the dispersion and damping characteristics of ion acoustic waves in

detail we need a Vlasov equation for each species. The counterpart to the dispersion

relation (7.27) now has an ion contribution so that

D(k,ω) = 1 −



∞

−∞



(u)

u − ω/k

du −



∞

−∞



(u)

u − ω/k

du = 0 (7.38)

It is often convenient to write the dispersion relation for electrostatic waves in terms

of the plasma dispersion function Z (ζ ), deﬁned by

Z(ζ ) =

√



∞

−∞

−ξ

ξ − ζ

dξ  ζ>0 (7.39)

266 Collisionless kinetic theory

Fig. 7.6. Landau damping of ion acoustic waves for (a) T

 T

and (b) T

∼ T

This function satisﬁes the differential equation



(ζ ) =−2

[

1 + ζ Z(ζ )

]

(7.40)