Boyd T.J.M., Sanderson J.J. The Physics of Plasmas
Подождите немного. Документ загружается.


6.6 Absolute and convective instabilities 247
Fig. 6.22. Dispersion curves for weakly coupled modes.
the ω(k) are complex and one of the pair has ω = ω
i
(k)>0 and so is unstable.
The instability is convective since for |ω|→∞the roots k(ω) are approximately
ω/v
1
and ω/v
2
and when ω
i
→∞, they fall in the same half k-plane. For v
1
,
v
2
> 0 they lie in the upper half k-plane. For real ω in the range (6.129) the roots
k(ω) form a complex conjugate pair. The root with k
i
(ω) < 0 has crossed to the
lower half-plane. Across the frequency range defined by (6.129) waves propagating
in the positive x-direction will amplify.
(d) Here k(ω) is real for all real ω but ω(k) is complex across the range (6.130).
The system is therefore unstable. Since v
1
v
2
< 0asω →∞it follows that the
roots k(ω) fall in opposite half-planes. The roots coalesce at a point in the upper

248 Waves in unbounded homogeneous plasmas
half ω-plane for which
ω = ω
c
= ω
0
+ 2i
√
(v
1
v
2
)
|v
1
− v
2
|
(6.131)
This corresponds to an absolute instability with growth rate ω
ci
.
Exercises
6.1 Obtain expressions for the phase and group velocities of the following
modes:
(i) Alfv
´
en: ω
2
= k
2
c
2
/(1 + c
2
/v
2
A
)
(ii) whistler: ω =−k
2
c
2
e
/ω
2
p
(iii) electron cyclotron (ω →|
e
|): ω
2
− ωω
2
p
/(ω +
e
) = k
2
c
2
6.2 Using the data in Table 1.1, compute Alfv
´
en wave speeds for plasmas in
(i) interstellar space, (ii) solar corona, (iii) ionosphere and (iv) tokamak.
Assume that the positive charges are protons in (i), (ii) and (iv) and oxygen
(O
+
) ions in (iii).
6.3 The energy density of a wave propagating in a plasma is the sum of con-
tributions from the oscillating electric and magnetic fields and from the
coherent particle motion induced by these fields. Suppose that the fields
show a small degree of exponential growth so that their behaviour with
time is described by exp(−iω
R
+ γ)t where γ ω
R
. The rate of change
of the energy density averaged over a period is given by
dW
dt
=
1
2
(E
∗
· j) +
1
4
∂
∂t
ε
0
|E|
2
+
|B|
2
µ
0
where ∗ denotes the complex conjugate. Writing
j
i
= iωε
0
[δ
ij
− ε
ij
(ω)]E
j
where ω denotes the complex frequency ω = ω
R
+ iγ , show, using a
Taylor expansion along with the relation (∂/∂t)|E|
2
= 2γ |E|
2
, that the
wave energy density may be expressed in the form
W =
1
4
ε
0
E
i
∂
∂ω
(ωε
ij
)E
j
+
|B|
2
µ
0
Apply this result to an electromagnetic wave propagating in an isotropic
plasma (B = 0), identifying the contribution to the energy density from
coherent particle motion.
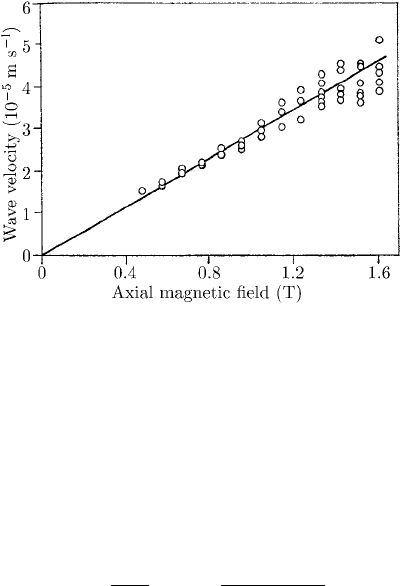
Exercises 249
Fig. 6.23. Measurement of the dependence of Alfv
´
en wave phase velocity on
axial magnetic field in a hydrogen plasma compared with theory (after Wilcox et
al. (1960)).
6.4 By introducing a term into (6.10) to allow phenomenologically for the ef-
fects of electron–ion collisions through a collision frequency ν
ei
, show that
the dispersion relation for electromagnetic waves in an isotropic plasma
becomes
c
2
k
2
ω
2
= 1 −
ω
2
p
ω(ω + i ν
ei
)
Hence show that electromagnetic waves are damped as a result of electron–
ion collisions, with damping coefficient γ = ν
ei
(ω
2
p
/2ω
2
).
6.5 Figure 5 shows the Alfv
´
en wave velocity, as a function of the axial mag-
netic field, measured in a hydrogen plasma by Wilcox, Boley and De
Silva (1960). The plasma temperature was 1 eV and the proton density
5 × 10
21
m
−3
. Using the cold plasma dispersion relation plot the Alfv
´
en
velocity as a function of magnetic field. Verify that the cold plasma ap-
proximation is valid in this parameter range. How might the discrepancy
between the measured phase velocities and those from the simple Alfv
´
en
dispersion relation be explained?
6.6 Show that the dispersion relation for a wave propagating orthogonally to a
magnetic field B
0
with its electric vector aligned with B
0
is ω
2
= ω
2
p
+k
2
c
2
.
Explain the physical significance of this result.
6.7 Show that the points of intersection of the plasma cut-off P = 0 with the
plasma resonance S = 0 and cyclotron cut-offs L = 0 in a two-component,
cold plasma occur at α
2
= 1, β
i
= 1 − m
e
/m
i
and α
2
= 1, β
2
i
= 1 −
m
e
/m
i
+ (m
e
/m
i
)
2
, respectively.

250 Waves in unbounded homogeneous plasmas
6.8 Verify the topological representation of the wave normal surfaces in the
CMA diagram, Fig. 6.12.
6.9 The wave normal surfaces corresponding to fast and slow modes coincide
when the discriminant (6.34) vanishes. Find the modes propagating along
the magnetic field for which this is possible.
For propagation orthogonal to the magnetic field show that there is a
curve in the CMA diagram on which coincidence is possible and obtain its
equation.
6.10 Determine the group velocity v
g
of the ion cyclotron wave satisfying the
dispersion relation (6.71) and show that v
g
→ 0asω →
i
. Show that the
wave is elliptically polarized, becoming LCP at the resonance frequency.
6.11 Derive (6.73) from (6.31). [Hint: Write (6.31) as n
2
= ( An
2
−C)/( An
2
+
A − B) and then substitute the biquadratic solution of (6.31) for n
2
on the
right-hand side.]
6.12 Determine the conditions under which the second term in the discriminant
in (6.94) is not small compared with unity.
Show that in ion acoustic waves, electron and ion velocities are of com-
parable magnitude.
6.13 Show that in a homogeneous isotropic plasma the conduction current and
displacement current in Langmuir waves cancel exactly.
6.14 Show that the dispersion relation for obliquely propagating ion cyclotron
waves in a warm plasma is
k
2
c
2
s
ω
2
=
2
2
i
c
2
s
+ v
2
A
(
2
i
− ω
2
)
v
2
A
(
2
i
cos
2
θ − ω
2
)
Rearrange this in the form ω = ω(k) and from this show that, in the
long wavelength limit (k
2
c
2
s
2
i
), ω
2
2
i
+ k
2
c
2
s
sin
2
θ. This mode
is electrostatic as is the mode in the limit k
2
c
2
s
2
i
. Write down the
dispersion relation for this case.
6.15 Consider how the ion cyclotron resonance changes when a plasma contains
two ion species, as for example in the solar wind which consists of protons
with helium ions as the principal minority constituent.
Plot dispersion curves k
2
v
2
A
/ω
2
versus ω/ for a plasma with 80%
protons and 20% He
++
ions for θ = 0 and θ = π/2.
Show that as propagation switches from θ = 0 towards θ = π/2 the
resonances move from the cyclotron frequencies to the frequencies deter-
mined by S = 0, with one of the resonant frequencies shifted to
ω
2
H−He
=
ω
2
pH
2
He
+ ω
2
pHe
2
H
ω
2
pH
+ ω
2
pHe
Exercises 251
while the other is displaced to lower frequencies.
6.16 Confirm that (6.120) can be written as a three-wave interaction as
kv
b
/ω
p
→ 1. Show that the maximum growth rate, corresponding to
k = k − ω
p
/v
b
= 0, is given by (6.121).
7
Collisionless kinetic theory
7.1 Introduction
Much of plasma physics can be adequately described by fluid equations, namely,
the MHD or wave equations. However, these are derivative descriptions in which
some information about the plasma has been suppressed. In situations where that
information matters it is necessary to go to a deeper level of physical description.
The information that gets lost in a fluid model is that relating to the distribution
of velocities of the particles within a fluid element, since the fluid variables are
functions of position and time but not of velocity. Any physical properties of the
plasma that depend on this microscopic detail can be discovered only by a descrip-
tion in six-dimensional (r, v) space. Thus, instead of starting with the density of
particles, n(r, t), at position r and time t, we begin with the so-called distribution
function, f (r, v, t), which is the density of particles in (r, v) space at time t. The
evolution of the distribution function is described by kinetic theory.
With the additional information on particle velocities within a volume element
introduced by a phase space description we now have microscopic detail that we
did not have before. For that reason, kinetic and fluid theories are identified as
microscopic and macroscopic, respectively.
At the most fundamental level we may define the distribution function in terms
of the individual particle positions and velocities by
f
K
(r, v, t) =
N
i=1
δ[r − r
i
(t)]δ[v − v
i
(t)] (7.1)
where the sum is over all particles of a given type. This is the Klimontovich dis-
tribution function which we have denoted by f
K
to distinguish it from f .Itis
a very spiky function being zero throughout (r, v) space except at the N points
[r = r
i
(t), v = v
i
(t)] where it is doubly infinite. However, we can generate a
smoother function by integrating (7.1) over a volume element rv about the
252

7.1 Introduction 253
point (r, v) which is large enough to contain a number of particles N
p
(r, v, t) 1
but small enough that
f (r, v, t) =
1
rv
r
dr
v
dv f
K
=
N
p
(r, v, t)
rv
(7.2)
does not change significantly over the dimensions of the volume element. Thus,
f (r, v, t) is the number density of particles in a small volume element centred at
the point (r, v) at time t.
Provided no particles are created or destroyed, f obeys a continuity equation
in (r, v) space which is derived by exactly the same arguments used to derive
the continuity equation for the mass density ρ(r, t) in Chapter 3. There are now
two divergence terms arising from the flow of particles through the surfaces of the
volume element in both r and v space. Thus, we have
∂ f
∂t
+
∂
∂r
· ( f v) +
∂
∂v
· ( f a) = 0 (7.3)
where a is the acceleration of the particles in the volume element. Since r and v
are independent variables in (7.3) we may bring v outside the differential operator
and, if in addition ∇
v
· a = 0, we get
∂ f
∂t
+ v ·
∂ f
∂r
+
F
m
·
∂ f
∂v
= 0 (7.4)
in which we have replaced a by F/m where F is the force acting on the particles of
mass m at the point (r, v) at time t. Such a partial differential equation describing
the evolution of the distribution function is known as a kinetic equation.
As a matter of fact, (7.4) is necessarily a collisionless kinetic equation since we
certainly cannot assume ∇
v
·a = 0 if we want to include the collisional interactions
taking place inside the volume element. A proper description of collisions is a
formidable problem as we shall see in Chapter 12. However, the transition from
(7.4) to a collisional kinetic equation can be made by a simple heuristic argument.
Assuming that F represents all the non-collisional (macroscopic) forces we note
that (7.4) states that
d f (r, v, t)
dt
=
∂ f
∂t
+
dr
dt
·
∂ f
∂r
+
dv
dt
·
∂ f
∂v
=
∂ f
∂t
+ v ·
∂ f
∂r
+
F
m
·
∂ f
∂v
= 0
i.e. in the absence of collisions f is constant along any trajectory in (r, v) space.
Collisions, however, change this so we write
∂ f
∂t
+ v ·
∂ f
∂r
+
F
m
·
∂ f
∂v
=
∂ f
∂t
c
(7.5)
254 Collisionless kinetic theory
where (∂ f/∂t)
c
represents the change in f with time due to collisions. This is then
the collisional kinetic equation, though how we represent the collision term in (7.5)
is a problem we defer until the next chapter.
In this chapter we are concerned only with collisionless kinetic theory for the
very good reason that most plasmas are essentially collisionless. All of the terms
in (7.5) have the dimensions of f times a frequency. The frequency appropriate
to the right-hand side is, of course, the collision frequency ν
c
while that on the
left-hand side depends on the dominant macroscopic force. Since this macroscopic
force is typically the Lorentz force due to the self-consistent fields the appropriate
frequency is likely to be one of the wave frequencies encountered in the previ-
ous chapter. In particular, we have noted the dominance of the electrostatic field
in maintaining charge neutrality and causing oscillations at the electron plasma
frequency in response to any local charge inequality. As the plasma frequency is
usually much greater than the collision frequency, unless we are specifically inter-
ested in collisional effects, we can ignore the collision term and take (7.4) as the
kinetic equation. We shall study it in order to discover some important properties
of plasmas which depend on distributions of the plasma particles in velocity space
and which, therefore, are not accessible to fluid descriptions.
7.2 Vlasov equation
Vlasov first solved the collisionless kinetic equation (7.4), now known universally
as the Vlasov equation, in the case where F = eE(r, t) and E is the self-consistent
electric field. Interestingly he did not solve (7.4) as an initial value problem and
consequently missed its most important property! This was subsequently discov-
ered by Landau and is discussed in the next section. The collisionless kinetic
equation is sometimes referred to as the collisionless Boltzmann equation but this
is something of a contradiction in terms since the representation of collisions is at
the very heart of the Boltzmann equation.
The first thing we shall do with the Vlasov equation is to show its formal equiv-
alence to the equation describing individual particle orbits. The latter is
m
¨
r = F (7.6)
having the solution
r = r(c
1
, c
2
,...,c
6
, t)
v = v(c
1
, c
2
,...,c
6
, t)
(7.7)
where c
1
, c
2
,...,c
6
are the six constants of integration, which might for example
be the initial values of r and v. Inverting (7.7) gives the formal solution
c
i
= c
i
(r, v, t)(i = 1, 2,...,6) (7.8)

7.2 Vlasov equation 255
Now any arbitrary function of the c
i
f = f (c
1
, c
2
,...,c
6
)
is a solution of (7.4) as one can see by direct substitution:
6
i=1
∂ f
∂c
i
∂c
i
∂t
+ v ·
∂c
i
∂r
+
F
m
·
∂c
i
∂v
=
6
i=1
∂ f
∂c
i
dc
i
dt
= 0
since the c
i
are constants of the motion. Thus the general solution of the Vlasov
equation is an arbitrary function of the integrals of (7.6), the equation describing
orbit theory. This was demonstrated by Jeans in work on stellar dynamics and so is
generally known as the Jeans theorem.
The formal equivalence of the Vlasov equation and particle orbit theory is rig-
orous and simple but, in one sense, slightly deceptive. It should not be imagined
that solving the Vlasov equation is as easy as finding some of the orbit solutions
obtained in Chapter 2. The reason is that, in the Vlasov equation, F contains both
external fields and self-consistent fields arising from the plasma motion. In Chap-
ter 2 we assumed that the latter were negligible compared with any applied fields
and so the orbit equations solved there are only approximations to the equation of
motion (7.6). We shall see later that there is a direct relationship between solving
the linearized Vlasov equation and calculating the simple (unperturbed) orbits of
the particles in the external fields. We note, in this context, that Jeans’ theorem pro-
vides a method of obtaining zero-order, equilibrium distribution functions, namely,
any function of the constants of the motion in the (zero-order) external fields.
Illustrations of this appear in later sections of this chapter.
For the moment, we observe that the full set of equations to be solved, in the
general case, is the Vlasov equation (7.4) for the distribution function of each
species of particle together with the Maxwell equations:
∇ × E =−
∂B
∂t
(7.9)
∇ × B = ε
0
µ
0
∂E
∂t
+ µ
0
j (7.10)
∇ · E = q/ε
0
(7.11)
∇ · B = 0 (7.12)
where
q =
α
e
α
f
α
dv (7.13)
j =
α
e
α
v f
α
dv (7.14)

256 Collisionless kinetic theory
and the sums are over the particle species. The fact that there are at least two
Vlasov equations to be solved (one each for ions and electrons) is a relatively minor
complication compared with the problem of solving the full Vlasov–Maxwell set
of equations self-consistently for f , when f itself is a source of the fields through
(7.13) and (7.14). (The equivalent of this latter problem in orbit theory would
be finding the orbits in the full self-consistent fields.) Nevertheless, the Vlasov–
Maxwell equations are the starting point for most calculations in plasma kinetic
theory. They include the principal effect of particle interactions, the self-consistent
field, and in the approximation that there are a large number of particles within the
Debye sphere (nλ
3
D
1), known as the weak coupling approximation (see Exer-
cise 7.3), they provide an adequate description unless we are specifically interested
in collisional effects. Their complexity means that one generally has to resort to
numerical methods even when a linear solution is sought. In the following sections
we present some important solutions of the linearized set of equations which are
amenable to analytic methods.
7.3 Landau damping
The most important and fundamental property of the Vlasov equation was dis-
covered by Landau (1946) who solved the linearized electron Vlasov equation for
F =−eE where E is the electric field created when a homogeneous plasma in
equilibrium is slightly perturbed. It is assumed that the perturbation is in the elec-
tron distribution only, so that the ions remain as a steady, homogeneous, neutral-
izing backgound. This simplifying assumption avoids having to solve two Vlasov
equations. Following Landau, we solve the linearized equation as an initial value
problem, i.e. the perturbation is introduced at t = 0. The alternative in which a
perturbation is introduced at r = 0 and its spatial evolution examined is considered
in Section 7.5.
Any steady, homogeneous distribution function f
0
(v) satisfies (7.4) identically,
since the electron density is uniform and equal to the ion density and there is no
electric field. If a small perturbation f
1
(r, v, t) is introduced, we may write
f (r, v, t) = f
0
(v) + f
1
(r, v, t) (7.15)
and, since the contribution of f
0
to E is zero, |E| is of order f
1
and the linearized
Vlasov equation is
∂ f
1
∂t
+ v ·
∂ f
1
∂r
−
eE
m
·
∂ f
0
∂v
= 0 (7.16)
where, from (7.11) and (7.13),
∇ · E =−
e
ε
0
f
1
dv (7.17)
