Boyd T.J.M., Sanderson J.J. The Physics of Plasmas

Подождите немного. Документ загружается.

6.4 Waves in warm plasmas 237

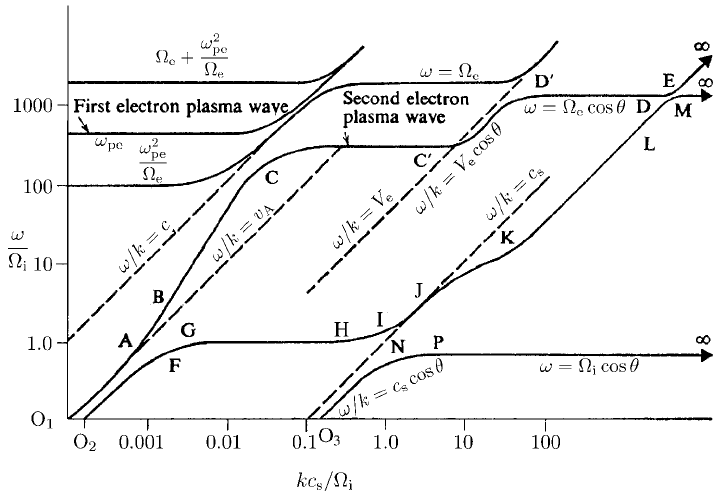
Fig. 6.15. Dispersion curves for oblique waves in very low β plasma with ω

< |

(after Stringer (1963)).

In general, the dispersion curves do not change appreciably as θ is varied pro-

vided the values 0 and π/2 are avoided. As θ → 0, for example, the gap between

the ﬁrst ion cyclotron–acoustic wave transition (HI in Fig. 6.13) and the slow

magnetoacoustic–second ion cyclotron wave transition (NP in Fig. 6.13) shrinks. In

the limit, the points (H, P) and (N, I) become coincident, that is, the curves O

G∞

and O

J now intersect. The transition from ﬁnite θ to 0 is shown in Fig. 6.16;

the presence of a transverse magnetic ﬁeld couples longitudinal and transverse

wave components so that the transverse Alfv

en wave passes into the longitudinal

acoustic wave while on the lower frequency branch a longitudinal mode passes into

a transverse mode. At θ = 0, however, no such coupling occurs and the transverse

shear Alfv

en wave now becomes a transverse ion cyclotron wave, as in the cold

plasma limit, while the other branch O

J is now entirely longitudinal. A similar

transition occurs between the electron cyclotron wave and the ion acoustic wave.

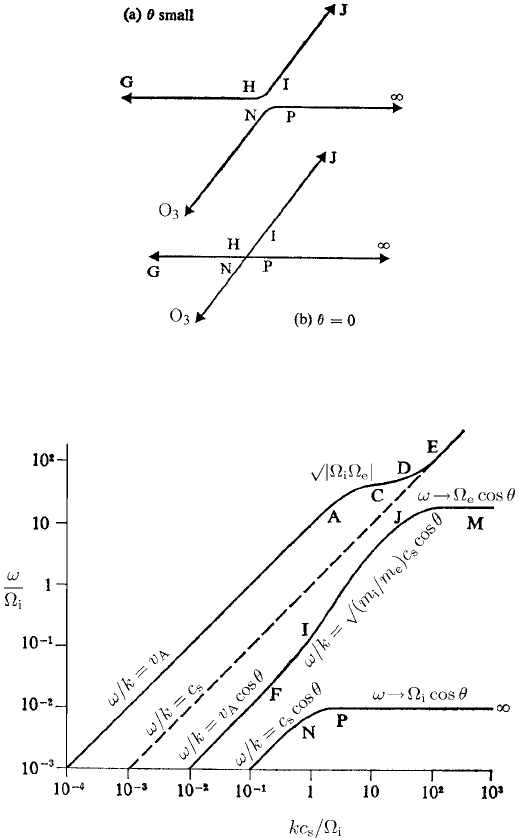
The situation as θ → π/2 is more complicated and will not be discussed; a

typical dispersion plot for the three low frequency branches is shown in Fig. 6.17.

Observe that only the O

CE branch survives in the limit θ = π/2 and that the

lower hybrid frequency (at which a resonance appeared for θ = π/2 propagation

in the cold plasma limit) now reappears as a pseudo-resonance.

238 Waves in unbounded homogeneous plasmas

Fig. 6.16. Coupling of longitudinal and transverse wave components in (a) for small θ

disappears in (b) for θ = 0.

Fig. 6.17. Dispersion curves for low frequency waves in low β plasma as θ → π/2.

6.5 Instabilities in beam–plasma systems

The waves that we have considered so far are those that may arise when we perturb

a plasma that is initially in equilibrium. In this section we take one step further

to investigate the perturbation of a steady state plasma; in particular, we allow

for non-zero ﬂow velocities u

0α

. Interstreaming or beam-carrying plasmas are of

widespread interest so this is an important generalization. The most signiﬁcant

6.5 Instabilities in beam–plasma systems 239

result of this extension of wave theory is the appearance of instabilities driven by

the plasma streams.

To keep the analysis as simple as possible we consider a cold, unmagnetized

plasma which, in the steady state, has interstreaming components. These may be

ions or electrons (or both) and there may also be a stationary background plasma.

Thus, the species label α now denotes the various components and we linearize the

cold plasma equations using, instead of (6.15),

n = n

+ n

u = u

+ u

E = E

B = B











(6.113)

where n

and u

are constants, obtaining for the equations of continuity and motion

∂n

∂t

+ ∇ · (n

+ n

) = 0 (6.114)

∂u

∂t

+ (u

· ∇)u

+ u

× B

) (6.115)

Note that we still have E

= 0, otherwise there would be no steady state. For

longitudinal waves (∇ × E

= 0) there is no magnetic ﬁeld perturbation so, again

for simplicity, we consider this case. Then we need only Poisson’s equation

∇ · E



(6.116)

to close the set.

Assuming that all perturbed quantities vary as exp i(k · r − ωt ), it is a simple

matter to obtain

ieE

m(ω − k · u

)

from (6.115) and substitute it in (6.114) to ﬁnd

ien

m(ω − k · u

)

Then from (6.116) we see that the condition for a non-trivial solution, E

= 0, is



pα

(ω − k ·u

)

= 1 (6.117)

where ω

pα

and u

are, respectively, the plasma frequency and steady state stream-

ing velocity for species α. This is the dispersion relation for longitudinal waves in

a plasma containing particle streams. Note that if all the stream velocities are zero

we recover the dispersion relation for longitudinal plasma oscillations.

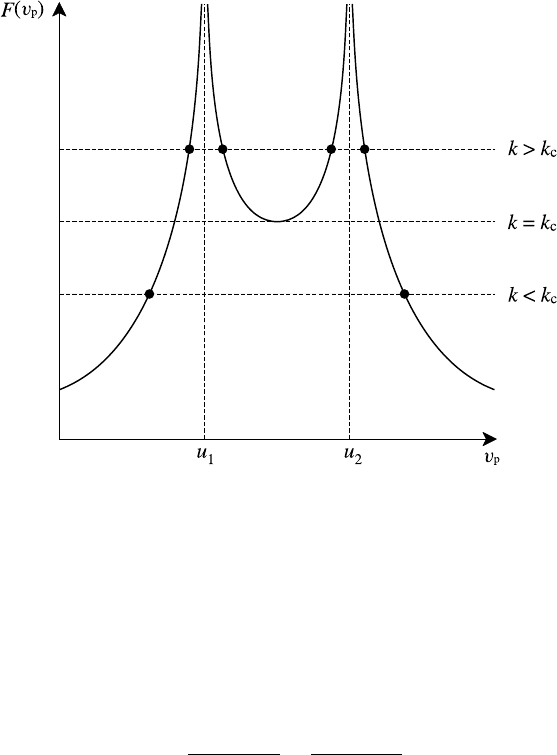
240 Waves in unbounded homogeneous plasmas

Fig. 6.18. Schematic plot of F(v

6.5.1 Two-stream instability

To demonstrate the onset of instability let us simplify further to the case of just

two streams with velocities u

and u

which are parallel (if they are not, we can

transform to a frame in which they are) and consider waves propagating in the same

direction. Then we may re-write (6.117) as

F(v

) =

− u

)

− u

)

= k

(6.118)

where v

= ω/k. The function F(v

) is sketched in Fig. 6.18 and we see that for

large enough k

there are four real solutions of (6.118). However, for k < k

there

are only two. Since (6.118) is a quartic equation in v

with real coefﬁcients there

must be four roots and for k < k

two of these form a complex conjugate pair

= (ω

± i γ)/k, representing exponentially growing and damped waves. The

growing wave solution is identiﬁed with the two-stream instability. The critical

value k

can be found by setting dF/dv

= 0 and is given by



2/3

+ ω

2/3



/(u

− u

)

(6.119)

On the basis of this analysis it appears that there will always be some waves, of

6.5 Instabilities in beam–plasma systems 241

Fig. 6.19. Two-stream instability dispersion relation showing the real and imaginary parts

of the frequency as functions of wavenumber.

long enough wavelength, which are unstable. This is another instance of the ﬂuid

description proving to be misleading. We shall see in the next chapter that when we

allow for the thermal spread in particle velocities and analyse the problem using

kinetic theory there appears a threshold relative velocity between the streams below

which there is no instability for any value of k.

For counterstreaming beams penetrating one wavelength in a plasma period, a

perturbation in density δn

on stream 1 will be ampliﬁed by particles bunching in

stream 2. And since δn

∝ n

, the perturbation grows exponentially in time. The

phase condition for this to occur is

− u

|(2π/ω

) ∼ (2π/k)

For u

− u

= 2v

this gives the condition for growth of the perturbation, i.e.

k ∼ ω

/2v

In the case of opposing streams of equal strength we may put ω

= ω

and u

=−u

= v

and from (6.118) the dispersion relation is

(ω − kv

)

(ω + kv

)

= 1

242 Waves in unbounded homogeneous plasmas

with solution

= k

+ ω

± ω

[ω

+ 4k

]

1/2

From (6.119) we see that instability occurs in the range 0 < k <

√

2ω

.The

maximum growth rate occurs at k = ω

√

3/2v

, obtained by setting dω/dk = 0,

and is given by ω = ω

/2. The dispersion curves for real and imaginary ω are

sketched in Fig. 6.19. The density perturbations grow until the electric ﬁelds which

they create become large enough to scatter the electrons causing dispersion in the

stream velocity which eventually extinguishes the instability.

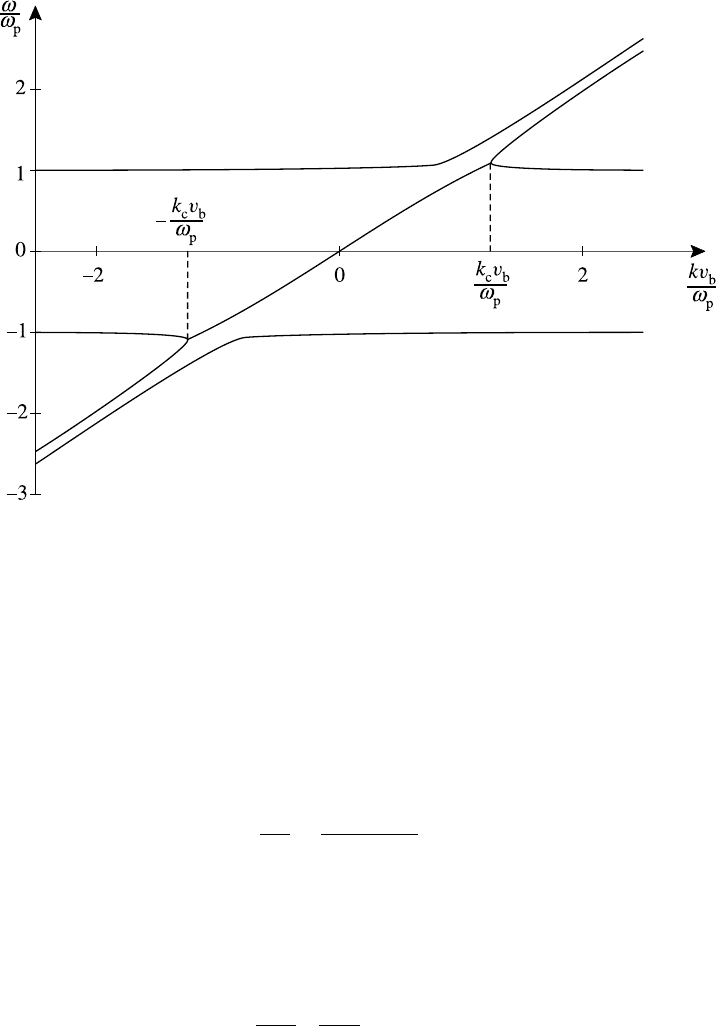
6.5.2 Beam–plasma instability

We can also use (6.118) to discuss the instability which arises when a single elec-

tron beam with number density n

and plasma frequency ω

ﬂows with speed v

through a stationary cold plasma. The dispersion relation is

(ω − kv

)

= 1 (6.120)

which may be written as

(ω

− ω

)[(ω − kv

)

− ω

] = ω

where the left-hand side shows the four linear waves (two normal modes, a Lang-

muir wave and an electron beam mode), while the term on the right-hand side acts

as a coupling term for these modes.

From (6.119), instability occurs for k < k

where



1 +





2/3



3/2

which, in the weak-beam limit, ω

 ω

, becomes k

= ω

. For this value the

beam modes have ω = ω

±ω

so that the interaction is three-wave with ω =−ω

well separated. By letting ω = ω

+ω, k = ω

+k and keeping only terms

of lowest order in ω

/ω

, (6.120) becomes

ω(ω − v

k)

= ω

The maximum growth rate is then

max

√

3(ω

)

1/3

4/3

(6.121)

Dispersion curves in the weak-beam limit are sketched in Fig. 6.20.

There is an interesting formal similarity between (6.120) and the dispersion

relation for an instability that appears when electrons drift through a neutralizing

6.5 Instabilities in beam–plasma systems 243

Fig. 6.20. Dispersion curves for weak-beam–plasma system with n

= 2 × 10

−3

background of stationary ions. This instability, ﬁrst identiﬁed by Buneman (1959),

will be discussed brieﬂy in the next chapter since it is properly set in the context

of instabilities in warm plasmas. Leaving that aside, if we simply identify the

electron–ion drift velocity v

with v

in the weak-beam case, we may write the

dispersion relation in the cold plasma limit (in the rest frame of the electrons) in

one dimension as

(ω − kv

)

= 1 (6.122)

Formally, ω

plays the role of ω

in (6.120) and so by analogy with (6.121) the

maximum growth rate for the Buneman instability is

max

√





1/3

≈ 0.05ω

for Z = 1.

244 Waves in unbounded homogeneous plasmas

Two-stream and beam–plasma instabilities are widespread in both laboratory

and space plasmas. Large electric ﬁeld ﬂuctuations have been measured in space

plasmas and streaming instabilities have been detected at the boundary of the

plasma sheet. Enhanced ﬂuctuations near the plasma frequency have been observed

upstream from the Earth’s bow shock and correlated with ﬂuxes of energetic elec-

trons.

6.6 Absolute and convective instabilities

In this section we return to consider in more detail the interpretation of complex

solutions to the dispersion relations, examples of which appeared in Sections 6.5.1

and 6.5.2. In these examples we supposed that the wavenumber was real and found

pairs of complex roots in the dispersion relation, corresponding to modes that

were either damped or growing in time. In practice it is often more convenient

to look for complex roots of the wavenumber k, for real frequencies. Then the

complex conjugate pair correspond to modes that are evanescent, i.e. the amplitude

of a disturbance decays with distance from its source, or spatially amplifying.

Beam–plasma systems have some parallels with electron beam–circuit systems.

For example, in travelling wave tubes an input signal is ampliﬁed by interacting

with beam electrons travelling down the tube synchronously with the electromag-

netic wave. Twiss (1950, 1952) ﬁrst drew attention to the distinct ways in which a

pulsed perturbation at some point in a physical system can evolve and emphasized

the need for a criterion to identify amplifying waves. Sturrock (1958) postulated

that the distinction between amplifying and evanescent waves is not dynamical but

kinematical and deciding which is which should be possible from a scrutiny of the

dispersion relation alone. However, to draw this distinction one has to consider not

a single mode but analyse instead the evolution of a wave packet.

A related problem appears when solving the dispersion relation for complex ω

roots in terms of real k. A wave packet may evolve in time in either of two distinct

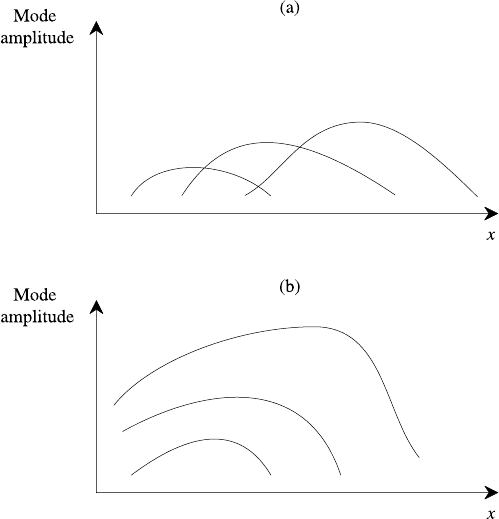
ways. Considering for simplicity an unbounded system, a pulse that is localized

initially at some point may propagate away from its source, growing in amplitude

as it propagates, as represented in Fig. 6.21(a). Given a sufﬁciently long time the

disturbance decays with time at any ﬁxed point in space. Instabilities with these

characteristics are classed as convective and the mode is said to be C-unstable.An

alternative outcome in Fig. 6.21(b) shows the initial pulsed perturbation spreading

across the entire region, with the amplitude of the disturbance growing in time

everywhere. Such instabilities are said to be absolute, the mode in question being

A-unstable. It is important to distinguish between these two possibilities. Clearly

one distinction can be drawn depending on the frame of the observer. An observer

in a frame moving faster than the speed at which an absolute instability spreads

6.6 Absolute and convective instabilities 245

Fig. 6.21. Pulse ampliﬁcation due to (a) convective and (b) absolute instability.

would classify the plasma as C-unstable. By contrast an observer in the frame

moving with the peak of the disturbance in Fig. 6.21(a) would see the mode as

A-unstable. Nevertheless, in practice there will usually be a preferred frame of

reference and hence a real physical distinction between convective ampliﬁcation

and absolute instability. This distinction takes on particular signiﬁcance in inhomo-

geneous plasmas where a mode may be unstable only over some localized region.

Then a convectively unstable mode can grow only as long as it is contained within

the unstable region. We shall return to this point in Chapter 11. While the terms

‘amplifying’ and ‘evanescent’ apply to the behaviour of modes with real ω,an

amplifying wave has essentially the same character as one that is C-unstable (real

k, complex ω).

6.6.1 Absolute and convective instabilities in systems with weakly coupled

modes

As an example of the classiﬁcation of instabilities as absolute or convective we

consider a dissipation-free system in which two branches of the dispersion relation

correspond to distinct linear modes. In the absence of any interaction between the

246 Waves in unbounded homogeneous plasmas

modes the dispersion relation simply factors into two branches, i.e.

(ω − ω

(k))

(

ω − ω

(k)

)

= 0 (6.123)

In the neighbourhood of a crossing point P at (ω

, k

) between the two branches

(k)  ω

+ (k − k

(k)  ω

+ (k − k



(6.124)

and v

are constant group velocities.

However, in general in the neighbourhood of such a point P the modes exhibit

coupling. If we suppose that this is weak then the dispersion relation for the coupled

modes in the neighbourhood of P may be represented by

[

ω − ω

− (k − k

][

ω − ω

− (k − k

]

=  (6.125)

where  is a small quantity. Equation (6.125) serves as a paradigm for mode-

coupling leading to instability in many physical systems including plasmas. Solv-

ing for ω(k) and for k(ω) gives in turn

ω(k) − ω



(k − k

)(v

+ v

) ±



(k − k

)

− v

)

+ 4



1/2



(6.126)

k(ω) − k



(ω − ω

)(v

+ v

)±



(ω − ω

)

− v

)

+4v



1/2



(6.127)

Admitting mode-coupling has the effect of shifting P into the complex plane. Rep-

resenting (ω − ω

) as a function of (k − k

) in Fig. 6.22 throws up four distinct

cases:

(a)>0; v

> 0 (c)<0; v

> 0

(b)>0; v

< 0 (d)<0; v

< 0



(6.128)

(a) The functions ω(k) are real for all real k and the system is stable. Moreover

the functions k(w) are real for all real ω and so the modes propagate without

ampliﬁcation.

(b) Here ω(k) is real for all k and so the system is stable. However k(ω) is

complex across the range of ω given by

(ω − ω

)

< 4|v

|/(v

− v

)

(6.129)

There is no propagation over this range, i.e. the modes are evanescent.

For

(k − k

)

< 4||/(v

− v

)

(6.130)